龙原湖公园上承式无铰拱桥空间有限元分析
姜 博
(合肥市规划设计研究院,安徽 合肥 230000)
1 引 言
随着我国桥梁建设技术的不断成熟,城市建设日新月异,各种高架桥、大跨度桥梁应接不暇。与此同时,城市公园的建设对桥梁景观性要求更高,其中中式无铰拱桥因其造型美观、经济适用更受青睐,但类似的有限元三维模拟研究甚少。以原阳县龙原湖公园1跨18 m无铰拱桥为例,运用MIDAS和CDN有限元软件建立三维空间模型,进行静、动力分析和抗震研究,为后续类似工程设计提供参考。
2 工程算例
2.1 工程概况
本桥位于龙原湖公园内,小桥碧水蓝天,共筑亮丽风景线。拱桥计算跨径18 m,常水位与河底最大高差为2.5 m。主拱圈采用矢跨比f/l=1/4.74的等截面钢筋混凝土,主拱圈厚度60 cm,宽7 m,腹拱拱圈为等截面混凝土圆弧拱,厚度25 cm;主拱圈拱上填料采用级配碎石,桥面9 cm沥青混凝土,下铺20 cm厚4.5%水泥稳定碎石。桥台采用重力式U形桥台,与拱脚处固结,在桥台与端腹拱处各设伸缩缝一道。承台尺寸6.6 m×10.6 m×2 m,下接6根直径1.6 m钻孔灌注桩。
桥址处场地地貌属黄河冲洪积平原,下部均为第四系全新统冲洪积层,土层自上到下特性详述如下。
①耕植土,层厚0.5~0.8 m;②-1、粉质粘土,层厚0.5~3.1 m;②粉土,层厚0.5-2.4 m;③粉砂,层厚0.8~4.6 m;④细砂,层厚20.0~25.4 m。该地区抗震设防烈度为8度,设计地震分组为第二组,设计基本地震加速度值为0.20 g,建筑场地类别为III类,场地特征周期值0.55 s。
2.2 有限元模型
采用有限元分析软件midas Civil建立拱桥空间有限元整体前处理模型,采用Civil Designer进行后处理分析,全桥共划分为230个节点,238个单元,见图1所示。主拱圈、腹拱圈及承台均采用梁单元模拟,桥面板采用虚拟梁单元便于布置车道荷载,且与拱圈之间采用弹性连接的刚性相连,将桥面板荷载传递至拱圈上。

图1 拱桥有限元模型图
主拱圈与台座采用刚性约束,采用m值法模拟土体对桩基的约束作用,桩底采用刚性约束[1-2]。假设土质是线弹性的连续介质,等代土弹簧刚度由土介质的动力m值计算,土弹簧刚度为:
=a×bp×m×z
(1)
式中:a为计算节点上下单元长度的一半之和,m;Bp为桩基的计算宽度,详见相关规范,m;m为土的比例系数,详见相关规范;z为各层土的中心(计算节点)到地面的距离,m。
3 静力分析
3.1 承载能力计算
根据模型分析结果,拱圈在承载能力极限状态下抗弯强度验算结果见图2。结果表明,主拱圈在基本组合作用下,正截面抗弯承载力满足要求。

图2 基本组合作用下正截面强度验算(单位:kN·m)
3.2 结构内力计算
根据模型分析结果,拱圈在频遇组合作用下的弯矩分布图见图3。
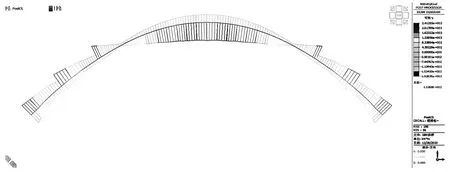
图3 频遇组合作用下弯矩包络图(单位:kN·m)
根据以上分析结果,无铰拱在运营状态始终处于压弯状态,因此,对于钢筋混凝土拱桥的验算可按偏心受压构件验算。在频域组合下,对拱圈主要控制截面进行裂缝宽度验算,计算结果见表1。

表1 主拱圈裂缝宽度验算结果
计算结果表明,主拱圈裂缝宽度验算满足《公路桥规》关于裂缝宽度不大于0.2 mm的要求。
4 动力分析
当行人或车辆的振动频率与桥梁结构的自振频率一致时,即形成共振,其振幅比一般的振动大的多。动力分析是用来确定桥梁结构的振动特性,即结构的固有频率和振型,它们是承受动荷载能力的重要参数[3]。模型计算前四阶自重频率分别为:一阶,4.64 Hz;二阶,5.86 Hz;三阶,7.01 Hz;四阶,7.13 Hz;计算结果表明,结构基频均大于3 Hz,能满足行人舒适度要求。
5 抗震分析
根据《城市桥梁抗震规范》,本桥位于公园内,为丁类抗震设防类别,因该地区抗震设防烈度为8度,故需要进行E1地震作用下的抗震分析和抗震验算,并应满足相关构造和抗震措施要求。地震作用采用反应谱法模拟。水平设计反应谱为[4]:
(2)
式中:T为周期,s;T0为反应谱直线上升段最大周期,取0.1 s;Tg为特征周期,s;Smax为设计加速度反应谱最大值,s。
水平设计加速度反应谱最大值Smax由下式确定:
Smax=2.5CiCsCdA
(3)
式中:Ci为抗震重要性系数;Cs为场地系数;Cd为阻尼调整系数;A为水平向基本地震动峰值加速度,m·s-2。
在地震作用下,对主拱圈主要控制截面进行抗弯强度和偏压强度验算,计算结果如表2所示。
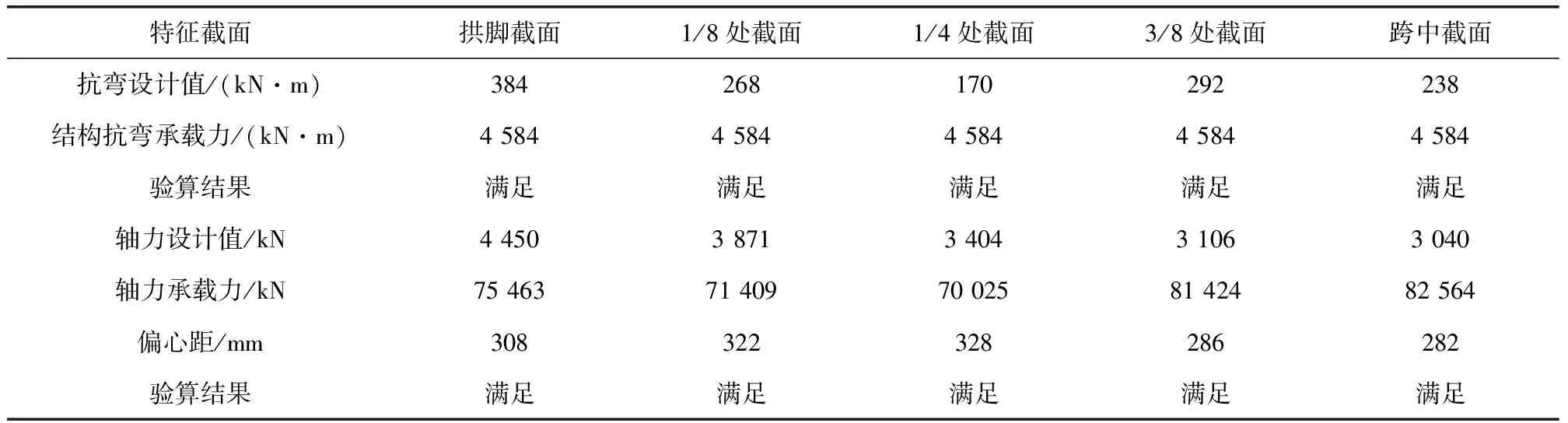
表2 主拱圈抗弯及偏压强度验算结果
计算结果表明,主拱圈在E1地震作用下满足抗弯和偏压强度满足规范要求,结构总体反应在弹性工作范围,基本无损伤,震后无修复即可恢复交通。
6 结 语
本文以龙原湖公园18 m景观拱桥为算例,借助空间有限元分析软件对上承式无铰拱桥进行了空间静力分析、动力分析以及抗震分析,分析结果表明:
(1)主拱圈在基本组合作用下,正截面抗弯承载力满足要求。正常使用状态下,主拱圈始终处于压弯受力状态,属于偏心受压构件,其裂缝宽度满足相关规范要求。
(2)通过Lanczos法分析无铰拱的动力特性,本桥自振频率均大于3 Hz,满足规范对上部结构的基频要求,体系结构合理。
(3)在E1地震作用下采用反应谱法进行抗震分析,抗弯和偏压强度满足规范要求,结构在弹性范围工作,基本无损伤。

