一种优化权重的k-近邻填补缺失值的算法研究

陈小杰

（重庆师范大学 数学科学学院，重庆 401131）

0 引言

在如今数据充斥生活的时代,数据的缺失问题引起了越来越多的学者的关注与研究。 一个完整的数据集才能更好地揭露事物的真实性,含有缺失值的数据集被称作不完全数据集。 现如今已经有许多方法被运用于不完全数据集的填补中,这些方法主要被分成两大类:机器学习填补方法与统计学填补方法［1］。 相对于统计学填补方法,例如均值填补法、多重填补法、期望值最大化方法,机器学填补算法因其能获得更多的有价值信息而受到各个领域的广泛运用,其中包括决策树、随机森林、支持向量机和k-近邻( KNN）填补算法［2］。 在这些算法中, KNN 操作简单、算法快速且有较成熟的理论支撑,在缺失数据填补中被广泛运用［3-4］。

k-近邻填补算法的基本思想是将整个数据集分成两个部分:完全数据集与不完全数据集。 完全数据集代表不含缺失值的数据集,不完全数据集代表含有缺失值的数据集。 在完全数据集中找到与目标填补值所在样本的k个最近邻样本,找到k个样本中缺失值所在的属性列对应的数据,即可得到与缺失数据邻近的k个数值,最后根据这k个数值去填补所缺失的数据。但是,在填补过程中由于每一个数据到目标填补数据的距离不一样,所以k个数据的贡献是不一致的。 本文就是在k-近邻填补算法的基础上,与主成分分析相结合,提出了基于熵权法的优化权重的填补算法,使得最后的填补效果更佳。

1 相关概念

1.1 KNN 填补算法

早在1968 年,Cover 和Heart 提出了原始的计算模型—— KNN 算法［5］。 在缺失数据填补应用中,它的原理简单易懂,通俗来讲就是“近朱者赤,近墨者黑”,即将缺失值作为目标值,找到与它距离最近的k个“邻居”,最后根据这k个数值的均值来填补缺失值,算法步骤如下［6］:

①输入m × n维数据集并进行数据初始化,构造数据矩阵:

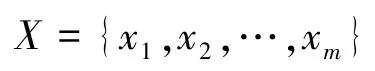
②计算出目标值(设为xir）所对应的样本实例与其他样本实例间的距离(传统KNN 算法采用欧式距离）:

在数据集X中找到与xir最邻近的k个数据点,即xir的k近邻数据；

③算出缺失值的替代值:

其中ωkr为k个最近邻数据的权值,取值为距离的倒数。

1.2 PCA 算法的应用

主成分分析(Principal Component Analysis）的主要目的是将关系“密切”的变量维数尽量减少。 通过计算,找到与原变量密切相关且相互正交的新变量,最后新变量组成的数据维度仍然为n维。 但是在前k(k ＜n） 个变量中,其方差值都是较大的,后面的 (n - k） 个变量所得的方差几乎为0,可直接忽略,从而达到将数据降维的效果［7］。 PCA 算法是应用最广泛的降维算法,在数据缺失的处理中也受到学者的青睐。

协方差是PCA 算法中很重要的量,协方差为正时,代表两个变量之间是正相关关系；协方差为负时,代表两变量之间是负相关关系；协方差为0 时,代表两个变量相互独立。 例如,三维数据(X,Y,Z） 的协方差矩阵表示为:

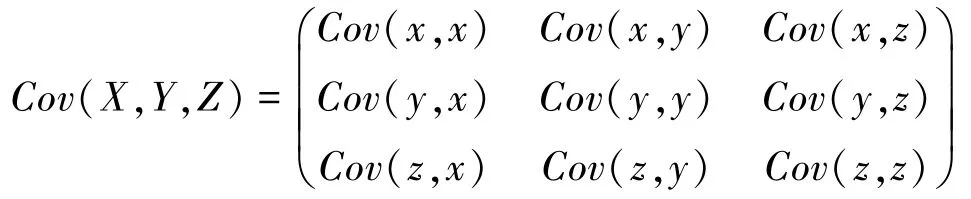
样本量X和样本量Y的协方差为:

2 优化权重后的填补算法过程

现在有许多学者将KNN 算法与PCA 算法进行结合,使得最后的填补效果较传统的KNN 填补算法更加有效。 但是在结合的同时往往忽略了k个近邻到目标数据的距离大小不一,所以仅仅用它们的均值或者用距离的倒数作为权值,这样的效果往往不理想。 接下来就是将这种填补算法进行优化,为了更加清楚地展示算法的过程,下面用一个简单的例子来说明,帮助理解后面详细的算法步骤。 表1 给出的数据集中,一共5个样本3 个属性,缺失值用？ 来表示。

表1 不完全数据集

2.1 KNN 填补算法预备工作

(1）对原始数据矩阵标准化。 原始数据集中包括m条数据记录,每一个数据记录的维度为n维,数据标准化可以消除量纲的影响。 而且,在数据大小不均衡的时候,也避免了大数据与小数据在计算过程中的权重影响,简化了后面的运算。

(2）确定距离的计算公式。 明考夫斯基距离(即明氏距离）可以用来计算两样本变量之间的距离,它可分为曼哈顿距离、欧氏距离和切比雪夫距离。 李航［8］表明将三阶明考夫斯基距离运用在KNN 算法距离中,效果更好,其公式为:

(3）k值的确定。k值的选取在算法中起着重要的作用。k值较小不能完全体现出目标值的特征,导致结果误差较大；k值较大会使大量的数据样本分成一类,从而对目标数据起较小作用的值也被纳入其中,使得最终的结果不理想甚至出现错误。 在一般情况下,k值的选取遵循(n为样本的容量）的原则。

在这个例子中,根据数据集首先得到表2 所示的完整数据集。

表2 不含缺失值的完全数据集

取k ＝2,按照上述过程可以计算出样本间的距离,样本3 与样本1、样本2、样本4、样本5 距离分别为:2.24,2.36,0.83,1.39。 找到与样本3 距离最近的两个样本具体结果如表3 所示。

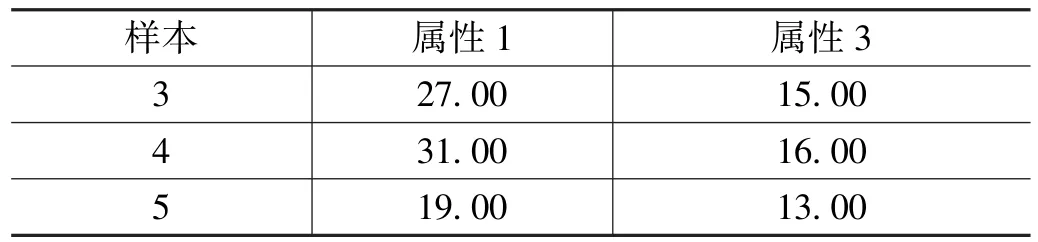
表3 最近邻样本

所对应的目标填补数据的两个近邻值如表4 中的数据。

表4 具体最近邻数据值

2.2 优化权重的KNN 填补算法

在运用传统KNN 算法填补缺失值时,直接利用均值去填补,或者距离的倒数来作为权值去填补,这样的结果会形成较大的误差。 直接用距离的倒数作为权重,会导致距离很近的两个样本量在直接取倒数后使得权重系数相差较大,最后的填补值效果不佳。 例如,上述例子中离目标值距离分别为0.83,1.39,两两之间距离仅仅相差0.56(＜1） ,代表两样本距离贴近,所占权重值相差不大,但是直接取倒数算出权重值,分别为1.20 和0.72,第一个数值比重接近第二个数值的两倍,加权平均后算出此时的填补值为32.45,效果不是很理想。 并且 AITTOKALLIOT［9］也提到,直接取倒数法会产生较大误差,所以权重的算法需要得到改进。 本文中的权重是在林晨欣［10］提出的熵权法的基础上进行改进的,并将其运用到KNN 算法中,改进后的权重计算公式如下:

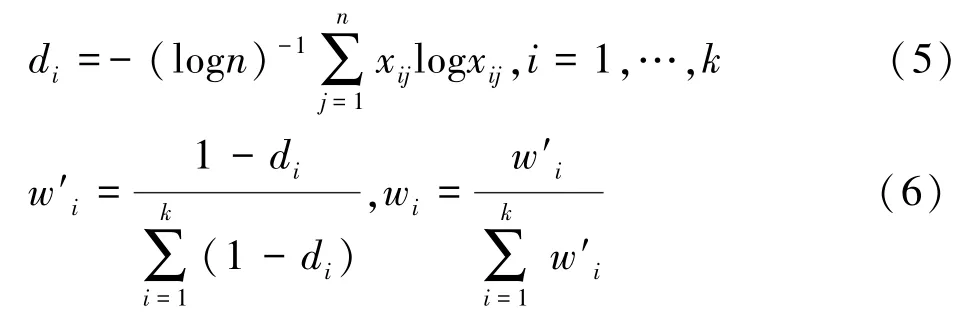
其中n为样本容量,xij为k个近邻样本中的元素(不包含缺失列）,wi即为最终的k个近邻数的权重系数。 该方法的优点在于不会受到距离较近的两个数据因直接取倒而权重系数相差较大的影响。

在例子中,可以计算得到两个样本的权重值分别为0.52、0.48,这样既保证了k个数据值贡献程度的不一,也避免了因为权重系数的过度波动而产生的误差。此时,填补值x0＝34.15。

2.3 结合PCA 算法原理得到最终填补值

上述分析中,根据距离公式得到了样本间的相关性,却忽略了特征之间也会相互影响。 所以,接下来结合PCA 算法原理,计算特征的影响值,具体操作过程如下:

(1）按照公式(3） 对原始数据求出协方差矩阵［9］,对于一个n维的数据来说可以得到一个n*n维矩阵,记为C:

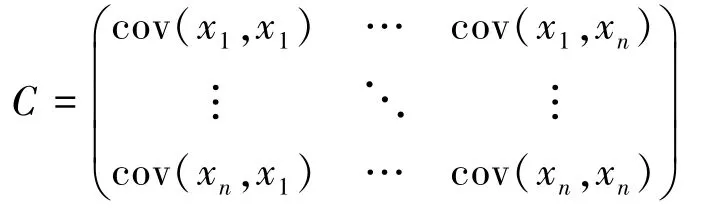
(2）对于k个样本变量的特征所对应的值可能不一致,算出每一个值的偏差:用每一个值减去本特征数值的均值。 结果记为ak:

m0为属性列中去掉缺失值后剩下的数据总数,xij为属性列中去掉缺失值后的所对应的剩余数据。

(3）在k个近邻值中,用上一步算出的偏差值与算出的协方差矩阵C中对应位置的协方差值相乘,然后取均值。 因为它表示了样本变量中特征所在维度的影响,所以将这个值称为维度影响因子,记为x′:

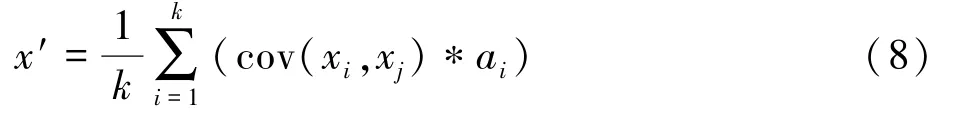
(4）得到最终填补值:

在上述例子中,两个近邻数据所算出的偏差值:a1＝-3.75,a2＝-8.75；影响因子值:x′ ＝-1.03。 所以最后的填补值就为:x ＝x0+x′＝34.15+(-1.03）＝33.12。

3 实证分析

3.1 数据来源

为了证明本文提出的新方法的有效性,将最后的结果与未设置缺失的原始数据进行对比分析。 实验数据来源于UCI 数据库中的iris (鸢尾花）数据集,数据集总共包含3 个类别,每一个类别包含50 个数据记录,并且每组数据记录包含4 个识别鸢尾花的属性,具体数据如表5 所示。

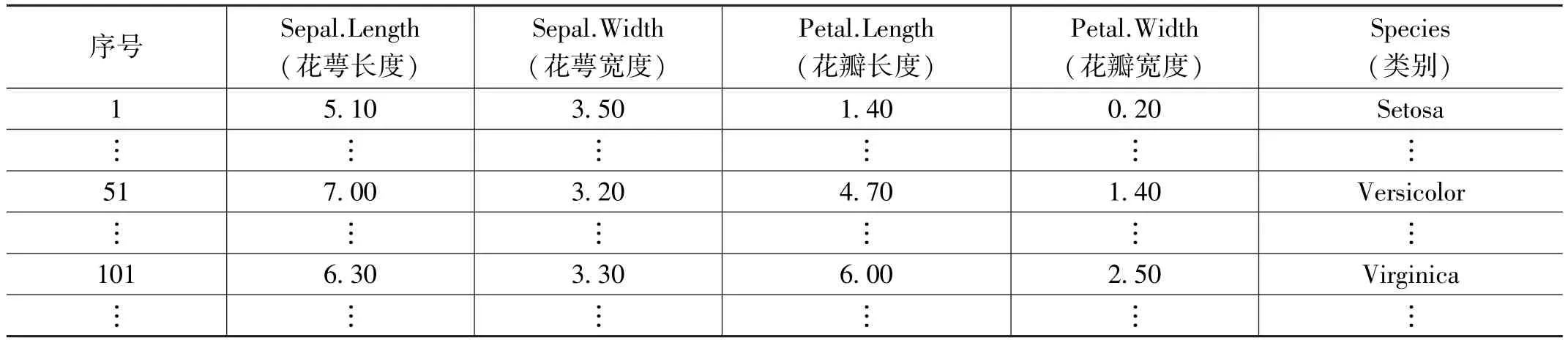
表5 鸢尾花原始数据集

3.2 检验方法

从原始数据表格可以看出所要操作的数据均为数值型数据,而均方根误差( RMSE）是衡量真实值与填补值之间差距的有效指标,所以现将此作为评价缺失数据填补效果的指标,其值越小代表填补数据效果越好。 其计算公式为:

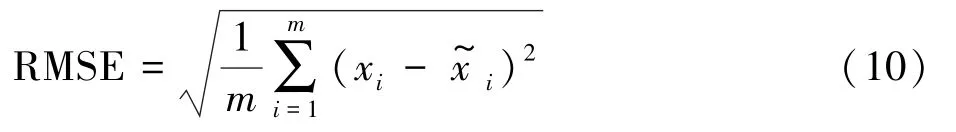
3.3 实验过程

在上述三个类别的数据集中,为了使缺失数据的填补效果不具有巧合性,采用在每个类别中构造缺失的方法:在Setosa 类别中构造第9 行Sepal.Width 属性缺失；在Versicolor 类别中构造第30 行Sepal.Width 属性丢失；Virginica 类别中使第11 行Sepal.Width 缺失。再分别用本文方法进行验证。 在数据集中,一个类别数据记录为50 条,记为样本容量n ＝50,根据k值选取原则,取k ＝7。 遵照上述KNN 填补算法,将缺失数据所在属性列作为目标列,取不含有缺失数据完整样本集(不包含目标列）,按照公式(4） 中的三阶明氏距离算出与缺失值所在样本的最近邻的k个样本量,可得到对应样本中目标列的数值,即作为缺失数据距离最近的k个“邻居”。 在3 种类别中得到的k个近邻数据见表6。

表6 3 种类别下k 个数据

在得到数据的7 个最近邻数据后,根据公式(5）、(6） 可以计算出赋予这k个数据基于熵权法改进的权重系数,加上最终的权重系数如表7 所示。

表7 基于熵权法改进后的权重系数

通过画图,可以得到改进权重系数前、后的关系。从图1 中的权重大致趋势图可以清楚地了解到,改进后的权重系数较传统的权重系数要稳定许多,与距离较近的几个数据所对应的权重系数也应相差不大的事实相符合,这表明改进后的权重系数缺失比传统的要优化许多。

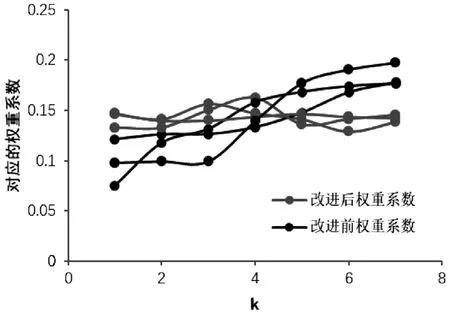
图1 优化权重前后的权重系数趋势对比

3.4 实验结果

在优化KNN 填补算法后,得到具体的填补值,但是在这个时候填补值效果不佳,与真实值还是有较大误差。 这是因为忽略了属性之间的影响,所以最后根据公式(7）、(8）可以算出3 个样本分别对应的k(k ＝7） 个数值具体的影响因子:0.078 0,0.021 6,0.034 1,最终填补结果如表8 所示。

表8 对比不同方法对缺失值填补情况

表8 可以看出,在缺失填补效果上,优化后的算法对于缺失值的填补效果更好,更贴近真实值,且最后的均方根误差相对传统的KNN 算法和一般权重KNN 算法要小许多,证实了本文优化算法的有效性与可行性。

4 结语

KNN 填补算法被广泛地应用在缺失数据的填补中。 熵权法作为赋予权重的十分有效的方法［9］,是在信息论的基础上提出来的。 本文主要在KNN 算法的基础上,提出了基于熵权法的优化权重系数,并且考虑到属性之间的相关性,在优化权重后的基础上,与PCA原理取得的属性相关影响因子相结合,得到最后的填补值。 这样的优点在于不仅考虑了目标数据最近邻数据的影响程度不一,将每一个“邻居”赋予更加稳定的权重系数,还考虑了属性相关的影响,使得最后的填补效果更加准确,更加逼近真实值。