基于双侧均值变点法的数字河网阈值划定——以南苕溪流域为例

聂启阳

(上海勘测设计研究院有限公司，上海 200335)

1 引言

近年来，随着卫星遥感、无人机倾斜摄影等测量手段的逐渐丰富，数字高程模型(Digital Elevation Model，DEM)为水文、生态环保等学科研究提供了极其广阔的运用场景[1]。DEM数据在使用各种流向算法后可生成表面流向栅格数据，再使用汇流运算可获得表征每个网格汇流数量的汇流累积栅格数据，目前已有HydroSHEDS、GDBD、JapanDir等分析产品[2～4]。在汇流累积栅格数据的基础上，往往使用一个集水面积阈值(CSA)来划定流域内的河道区域与非河道区域，因此阈值选取的大小将直接影像河网提取的细致程度和后期研究的适用程度[5]。目前阈值选择方法的主要基于2个方向：①根据已有蓝线数据进行对比，寻求与蓝线形态拟合最佳的阈值；②根据流域阈值-河网密度曲线，选取变化趋于平缓的点对应阈值最为最佳阈值[6～8]。第一种方式受制于蓝线数据的精度及获取难度，在小区域或无资料地区难以运用；后者应用简单，且不受制于其他资料，自身基于地形演化原理具有较高的理论支撑，已有众多研究使用均值变点法检测这一平稳点的位置，用于改进其主观性。然而不同研究对象的实际运用研究中，汛期和非汛期河网具有较大差异，已有研究表明流域河网存在多个阈值，主要可分为：①曲线由急剧骤减到逐渐减少的“阈值点”，表征坡面上河网链消失的阈值分界点；②曲线由逐渐减少到逐渐平稳的点，用于表征小型沟道上河网链消失的阈值分界点[9]。本次研究基于双侧均值变点法，在南苕溪流域开展数字河网提取验证，寻求一种客观有效的河网双阈值划定方式，以期为后续水文、生态环境模型研究的数据前期处理提供参考。

2 研究区域及数据

2.1 研究区域概况

南苕溪流域位于浙江省杭州市，流域面积约720 km2，全长约63 km。流域地处中亚热带季风气候区南缘，年雨量充沛多年平均降雨量为1460 mm，降水集中在4～9月份，多年平均气温15.8 ℃[10]。

南苕溪自东天目山水竹坞发源，并由浪口溪、南溪和锦溪3条主要支流组成，浪口溪南流经里畈水库至浪口汇入南溪后称南苕溪，东流穿过临安城区于青龙口汇入锦溪后入青山水库。浪口溪和南溪河段地处浙西山丘区，河道坡降较大，土地利用类型也存在差异，浪口溪以天然林覆被为主，南溪沿岸雷竹林广泛分布。锦溪河段地势相对平坦，依次流经上游农业区、玲珑工业区和临安市区[11]。南苕溪在汇入东苕溪后，最终汇入太湖(图1)。

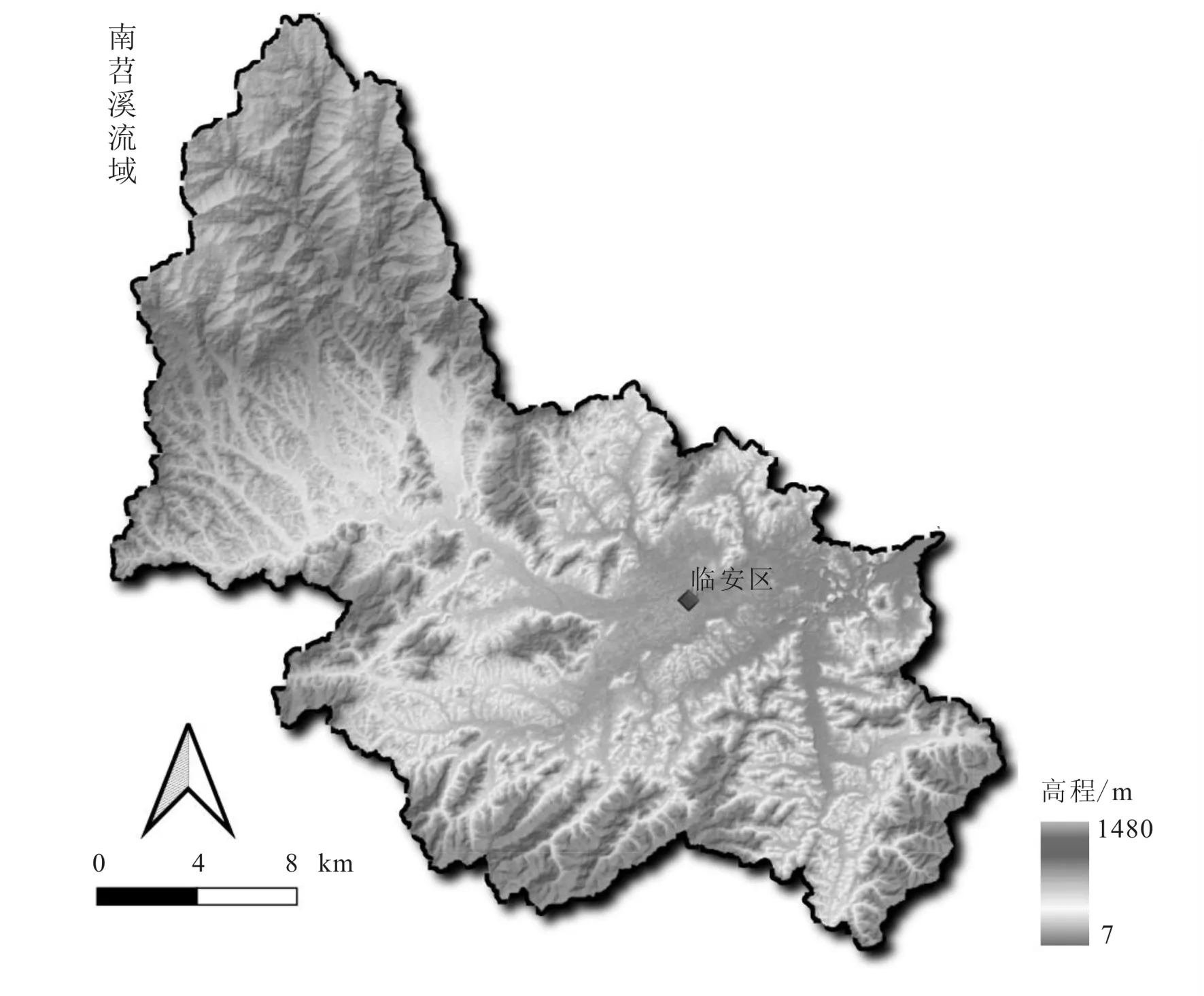
图1 研究区域地理地貌

2.2 数据来源及处理

本研究使用的DEM数据来源为ASTER GDEM V3，此数据集由日本经济产业省(METI)和美国国家航空航天局(NASA)在2019年8月联合发布。数据垂直分辨率为1 m，水平分辨率为30 m。具有较高的准确度，已得到国内外的广泛运用[12～15]。(https://asterweb.jpl.nasa.gov/gdem.asp)。

DEM后续处理采用一种优先洪水算法改进的D8流向算法[16]。该算法无须对DEM进行前期填洼，因此不会改变DEM信息，可解决过度填洼产生的平行河网问题，对于本研究区下游较为平坦的城市区域较为合适[17]。

该算法以优先洪水算法的漫水思想为基础，对DEM虚拟出由外至内的淹水过程，从外侧最低网格淹没开始至DEM最高网格被淹没为止，反向记录此流程就形成了整个地形内水流的整体流向趋势。二维示意图详见图2。图2a反应的是漫水过程，外围漫水过程从右端f开始至e，随后由a至b，b至c，最终e和c至d完成整个栅格的淹没过程。反向记录整个流程即可得到流向栅格数据，同时因为是单流向算法，因此结合D8的最陡下降原则判定具有多流向趋势的栅格，其中d具有流向c和e的趋势，根据最陡下降原则确定d流向e。因此整个流向方向为图2b：d流向e再流向f，c流向b再流向a，最终流出整个流域。整体来看对于外流型流域，该流向算法识别性强，有较强的物理过程支撑，无需填洼，能有效地解决填洼导致的平行河网问题。

DEM经过处理后得到地表流向栅格数据，再通过汇流累积算法获得汇流累积栅格数据。常用的汇流累积算法采用一套递归：首先初始化汇流累积栅格数据均为1，对每一栅格进行判定，若其汇流累积值为1则根据地表流向栅格数据判定其四周8个网格流向它的栅格，求和满足要求的栅格汇流累积值，在加上该栅格的初始值1。遍历所有栅格，获得整个区域内的汇流累积栅格数据，因为分水岭仅流出，周围无网格流向它，因此其汇流累积值为0，因此再对整个区域汇流累积栅格数据-1，得到最终的汇流累积栅格数据。

3 研究方法

3.1 双侧均值变点法

双侧均值变点法为均值变点法的变式，均属于数理统计方法。针对河网阈值问题其离散化模式为以下状态：

阈值序列为a，长度为n，其值为a1、a2、…、an-1、an，对应计算的河网密度序列为b，长度为n，其值为b1、b2、…、bn-1、bn。

图2 水流整体流向趋势二维示意

河网密度计算使用：

(1)

式(1)中，Ln为阈值序列对应的河网长度，A为流域面积。

令m=2、3、…、n-4、n-3，k=m+2、m+3、…、n-2、n-1，m和k将序列河网密度n分割为3段。

计算各段内的算术平均值：

(2)

(3)

(4)

进而求得各段统计量：

(5)

(6)

(7)

求和各段统计量：

Smk=SⅠ+SⅡ+SⅢ

(8)

式(8)中，Smk为m、k在河网密度序列上的统计量，Smk的最小值所的m和k所对应的am与ak为曲线由急剧骤减到逐渐减少的“阈值点”和曲线由逐渐减少到逐渐平稳的“阈值点”。

3.2 研究流程

对研究区域内DEM处理后得到的汇流累积栅格数据进行集水面积阈值采样获得阈值序列，划定各采样集水面积阈值下的河网栅格数据，进而求得对应的河网密度序列。将两序列使用双侧均值变点法进行运算，获得对应的两个“变点”。得到两个集水面积阈值参数，提取对应的数字河网数据在卫星图上叠加对比，分析提取准确度及特点。

4 研究结果

4.1 双侧均值变点结果

本研究中，南苕溪流域DEM经上述处理后取样序列长度为100，得到阈值密度曲线成果详见图3a，双侧均值变点检测成果详见图3b。

由图3a可知，随着集水面积阈值的增加，河网密度的下降有显著的3个阶段：①首先是河网密度随集水面积阈值增大的急速下降阶段，表征各微小坡面汇流的骤缩，由于流域中大量的坡面网格汇流累积数较低，因此该阶段，集水面积阈值的变化将导致河网长度的急剧减小，从而引起河网密度的急剧陡降，直至达到表征坡面上河网链消失的阈值分界点，曲线才开始由急剧骤减到逐渐减少；②紧接着是以一个较慢的速度下降阶段，表征小型沟道部分的逐步排除过程，由于流域中存在不少的坡面网格汇流累积数为中低等级，因此该阶段，集水面积阈值的变化导致河网长度的逐渐减小，从而引起河网密度的逐渐下降，直至达到表征坡面上小型沟道上河网链消失的阈值分界点，曲线才开始由逐渐减少到平稳下降阶段；③最后是一个平稳下降阶段，流域中微小坡面汇流与小型沟道已完全排除，留下显著的中大型沟道，由于流域中坡面网格汇流累积数较大的网格存在数量较少，因此该阶段，集水面积阈值的变化导致河网长度的减小程度微弱，从而引起河网密度的下降程度也显著平稳。

由图3b可知，整体统计量Smk变化较为连续，整体起伏变化不复杂，呈现中间低，四周高的形态。其中，m=1，k=2；m=99，k=100；m=1，k=100这三类情况下统计量Smk最高，分割的阈值密度曲线3个区域内部变化趋势一致性最低。而当m=21，k=45时统计量最低，表明此状态下分割的阈值密度曲3个区域的内部变化趋势一致性最高。对应的河网密度随集水面积阈值增大而呈现的3个阶段：急速下降阶段、较慢的速度下降阶段、平稳下降阶段对应统计尺度上最合理。因此可得到该状态下的对应集水面积阈值分别为：a21=2517和a45=8936，分别提取上述集水面积阈值下的流域数字河网叠加至卫星影像进行对比验证。

图3 (a)河网密度-阈值曲线，(b)双侧均值变点检测

4.2 河网划定结果

集水面积阈值为a21=2517和a45=8936所生成数字河网详见图4，由图4可见，数字河网与地形吻合程度均较高，河网在上游山丘区山谷发育较为集中，下游平缓城市地带未发现平行河网问题。集水面积阈值为2517时相较于集水面积阈值为8936时，河网往上游延伸的程度显著增加，河网长度与河网密度也更高。从河网分布的状况来看，南苕溪流域内小型沟道部分集中在中游及上游，下游多为坡面的微小坡面汇流。

局部卫星影像对比上更明显看出数字河网在山谷地形间所体现的较高准确度，图4(a)、(b)均为西北上游部分，该部分局部对比可看出a45=8936所生成数字河网在a21=2517所生成数字河网基础上往干流部分收缩程度显著提高，对于山谷上游部分汇流面积较小的部分均排除，仅保留汇流规模有所保证的主干河道与沟槽，因此对于长时间序列径流、生态环境模拟，可选择a45=8936所生成数字河网。关注程度集中在显著的河道沟槽中，排除上游汇流面积较小干扰。

局部卫星影像对比图4(c)、(d)位于西侧和南侧的河流末端分叉口，由对比图可见，a45=8936所生成数字河网在a21=2517所生成数字河网基础上河道分叉显著降低，往上游的小型沟道未包含入数字河网范围，而后者对于小型沟道的分叉、汇流、形态描述更为细致准确，因此对于短时间序列洪水等灾害模拟，可选择a21=2517所生成数字河网，暴雨情况之下，河流整体水位抬升，流域整体土壤含水量较高，平时水流较少的小型沟道内也将形成显著的径流过程，因此对于该部分描述更为详尽的数字河网更适合雨洪情景下的地理表达。

总的来看，双侧均值变点法所得集水面积阈值为a21=2517和a45=8936生成的南苕溪流域数字河网均能达到准确、合理的基础要求。而a45=8936所生成数字河网收缩程度更高，河道分叉程度更低，接近非汛期及长晴期阶段流域河网条件；a21=2517所生成数字河网对于小型沟道的分叉、汇流、形态描述更为细致准确，接近汛期及降雨条件下的流域河网状态。后期研究中可针对研究问题选择不同特征的数字河网，以达到更符合实际场景的表达。

图4 双阈值划定数字河网对比验证

5 结论

(1)双侧均值变点法分割的阈值密度曲线3个区域内部变化趋势一致性最高，3个区域对应河网密度随集水面积阈值增大而呈现3个阶段：急速下降阶段、较慢的速度下降阶段、平稳下降阶段。

(2)双侧均值变点法所得两个集水面积阈值生成的数字河网均能达到准确、合理的基础要求。而高阈值所生成数字河网收缩程度更高，河道分叉程度更低，接近非汛期及长晴期阶段流域河网条件；低阈值所生成数字河网对于小型沟道的分叉、汇流、形态描述更为细致准确，接近汛期及降雨条件下的流域河网状态。

(3)基于双侧均值变点法所划定的数字河网可针对研究问题选择高低阈值的数字河网，以达到更符合实际场景的表达。低阈值生成的河网适合做短时间序列洪水等灾害模拟，高阈值生成的河网适合做长时间序列径流、生态环境模拟。