基于ARIMA 模型与随机森林模型的零售服装动态销售预测模型探析

徐 琪，张阳奎

（东华大学 旭日工商管理学院，上海 200051）

0 引言

时尚服装由于具有季节性、时尚性、易贬值等特点，在竞争激烈的市场环境中，常常会出现缺货或积压的情况。因而，提高控制时尚服装库存水平，对于时装零售商的盈利至关重要。而库存与销售预测直接相关,销售预测不仅影响库存及公司的盈利，而且影响服务客户质量。当面临缺货时，客户可能决定在其他零售商处购物。另外，时装行业的供应链较长，涉及众多参与者，如原材料的供应商、制造商、分销商和零售商，导致各参与方在未准确了解客户需求的情况下，为了时尚服装产品的生产与销售而提前下订单，从而产生供应链上的牛鞭效应。

为了准确进行销售预测，多年来研究人员提出了很多统计分析方法，使用频率较高的有指数平滑法、回归分析法、自回归积分滑动平均模型（Autoregressive Integrated Moving Average Model，ARIMA模型）等。近年来，神经网络等深度学习方法被大量研究人员用于销售预测，但深度学习模型是一个黑箱模型，预测结果的可解释性不强。另外，深度学习模型在不同的场景下，预测性能并不稳定，而且神经网络的层数、隐层节点数等参数都需要研究人员依靠丰富经验去调整，这会耗费大量预测时间，因而基于深度学习的预测方法在应用上存在一定的局限性。

文章综合考虑时尚服装历史销售因素、节假日因素、宏观经济因素以及天气因素对时尚服装销售量的影响，结合基于时间序列的ARIMA 模型与机器学习中的随机森林模型，构建了一种新的时装销售组合预测模型。该模型能够提升预测精度，并且预测所需的时间也比基于深度学习的模型短，可解释性更强。文章最后用实例验证了模型的有效性，以便得到有价值的结论。

1 模型的构建与求解

文章将零售服装最终销售额（

Y

）分解为时尚流行趋势因素影响下的销售额（

T

）、季节性因素影响下的销售额（

S

）、周期性因素影响下的销售额（

C

）和不规则变动因素影响下的销售额（

I

）4 个部分，用公式（1）表示：

ARIMA 模型能够捕获到时间序列中的相关的趋势因素

T

，如时尚服装的流行趋势。而随机森林模型作为机器学习中具有监督、层次结构的决策树的集成模型，通过输入时尚服装销售相关的训练数据，不断调参与迭代，能够捕捉到训练数据集中天气、经济环境、节假日因素与销售额之间的非线性关系（

S

+

C

+

I

），进而用于时尚服装的预测，因此考虑将这两个模型加以融合，形成一种新的时尚服装销售组合预测模型，以预测时尚服装的销售额。

1.1 基于服装历史销售记录的ARIMA 销量预测模型

建立ARIMA 模型一般有3 个阶段，分别是模型识别和定阶、参数估计和模型检验。文章构建的时尚服装销售预测的ARIMA 模型（

p

,

d

,

q

）时间序列如（2）所示：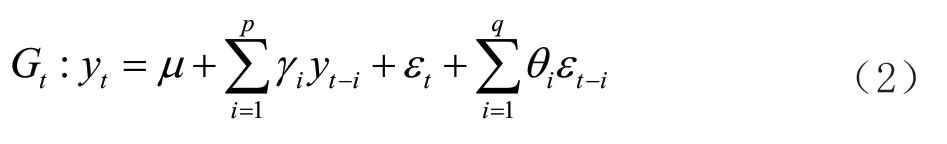

式中，

y

为当前预测的销售额；

μ

为常数项；

ε

为白噪声序列；

p

为自回归阶数；

d

为差分次数；

q

为移动平均阶数；

γ

为自回归系数；

θ

为白噪声序列的权重因子。时尚服装的原始销售数据受到多种因素的干扰，可能是非平稳的时间序列数据，因为平稳性是时间序列分析的先决条件，所以需要对不稳定的服装销售历史数据序列进行处理，将其转化为平稳的序列，然后进行模型的识别和定阶。这里主要是确定自回归阶数

p

、移动平均阶数

q

这两个参数。确定这两个参数以后，需要对每一阶的系数进行参数估计，得到系数的估计值以后，将其带入模型，对模型进行适应性检验，检验通过后，对用得到的模型进行预测，将预测值与真实值进行对比，从而确定模型的有效性。1.1.1 差分次数

d

的确定ARIMA 模型可看作是AR+I+MA 的组合，其中I的作用是通过对原序列进行差分运算使得差分后的序列具有平稳性，即差分后的时间序列的噪声

ε

为白噪声，满足

ε

WN(0，

σ

)。为了使得序列变得更加平稳，首先要确定差分次数。笔者用

X

表示零售服装销售额所构成的时间序列，

x

表示序列中第

t

个点代表的销售额，

t

=1,2,3…

N

，

N

表示序列

X

的长度。记符号Δ为差分算子，一阶差分表示为：Δ

x

=

x

-

x

，相应的，

d

阶差分可用（3）表示：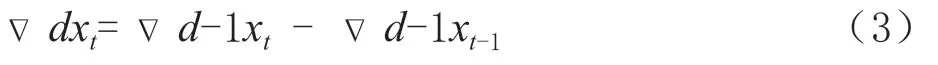

首先对原始的销售额时间序列按式（3）进行

d

阶差分，然后对差分后的时间序列做平稳性的adf 检验得到最佳差分阶数。1.1.2 ARIMA 模型中参数

p

与

q

的确定通过式（3）的差分方法对原始销售额时间序列进行差分，使得时尚服装销售额的时间序列平稳以后，即可建立ARMA（

p

,

q

）模型，ARMA（

p

,

q

）模型是由AR(

p

)和MA(

q

)模型组合得到的，其中AR(

p

)模型可以用（4）表示：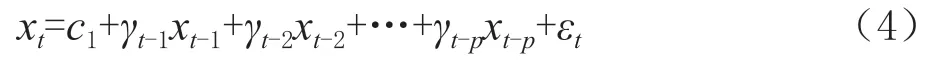

MA(

q

)模型可以用（5）表示：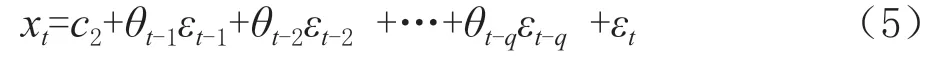

AR(

p

)+MA(

q

)模型的组合ARMA(

p

,

q

)表达式（6）如下：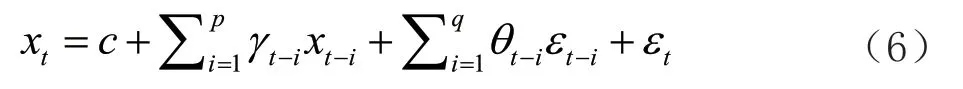

式中，

c

为常数项；

ε

为白噪声，满足

E

(

ε

)=0，Var(

ε

)=

σ

；

γ

为自回归系数；

θ

为白噪声序列的权重因子；

p

为自回归阶数；

q

为移动平均阶数。用

X

表示服装销售额所构成的时间序列，

x

表示序列中第

t

个点代表的销售额，

t

=1,2,3…

N

，

N

表示序列

X

的长度，则该销售额时间序列的均值和方差分别为：

μ

=

E

(

X

)，

σ

=

D

(

X

)=

E

(

X

-

μ

)。定义滞后

k

阶的销售额时间序列自相关系数（

acf

）和偏自相关系数（

pacf

）分别为（7）和（8）：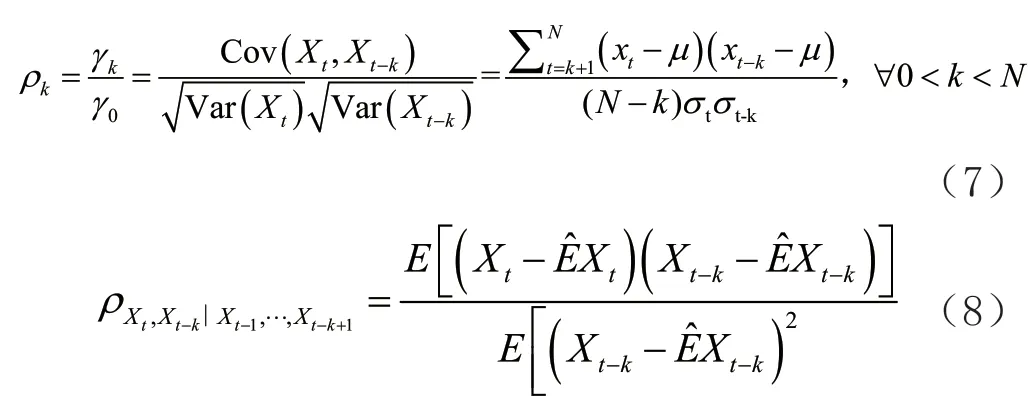

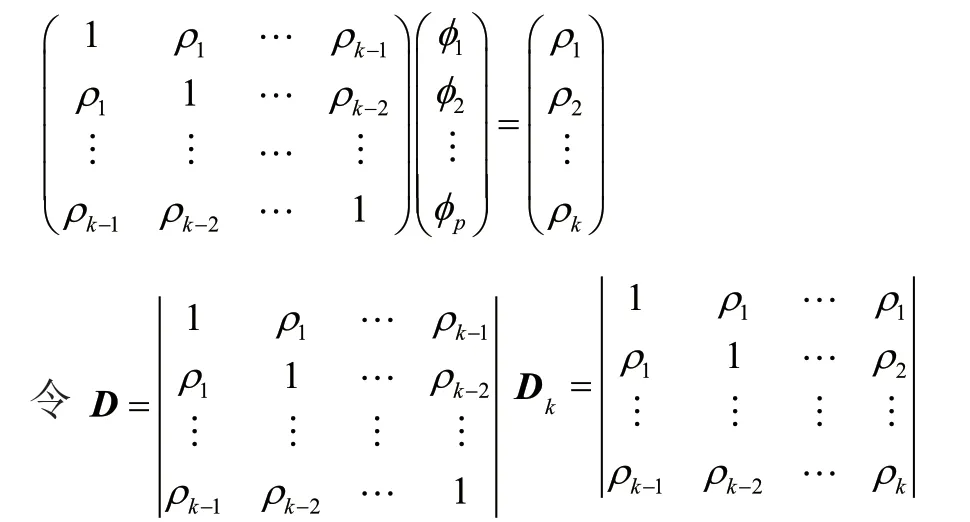
因为式（8）无法直接求解，需要使用Yule-Walker方程进行转化并化简后进行求解。Yule-Walker方程写成矩阵形式为：

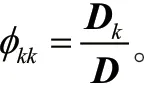
由以上建模和求解过程，结合文献中使用的相关定阶方法，得到初步定阶，在初步确定阶数范围之后，再根据赤池信息准则（Akaike Information Criterion，AIC）确定最佳定阶。

1.1.3 权重参数的极大似然估计

假设{

X

,

t

=0,±1,±2,…}是经过中心化后的ARMA(

p

,

q

)序列，已取得销售额的时间序列样本，它的概率密度函数为式（9）：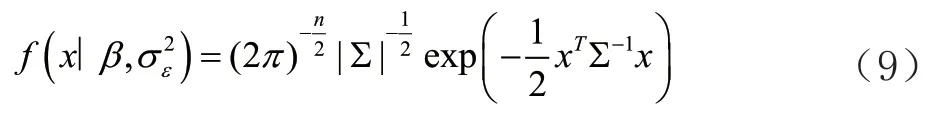

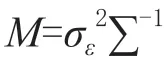
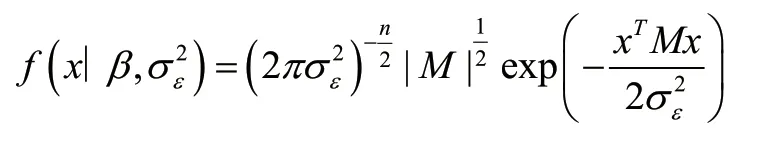
根据式（9）可得对数似然函数为式（10）：

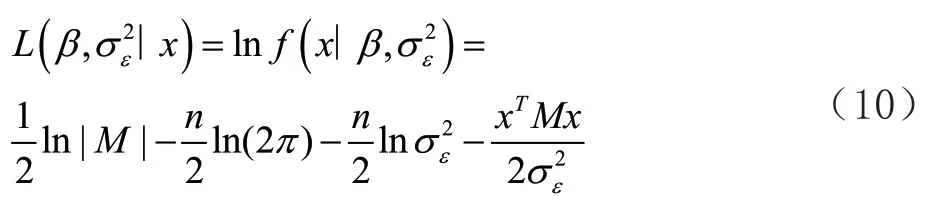
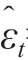
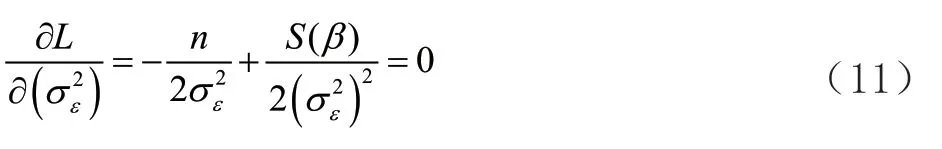
根据式（11）可求出：

将其带入（13）：

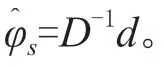
1.1.4 基于ARIMA 模型的服装销售预测

根据前面所构建的ARIMA 模型，进一步利用该模型进行服装销售预测。根据式（4）AR(

p

)模型对销售额时间序列的前

s

步进行预测，其预测方法公式（15）表示如下：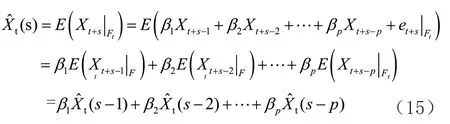

根据式（5）MA(

q

)模型做服装销售额时间序列的前

s

步预测，其预测方法用公式（16）表示如下：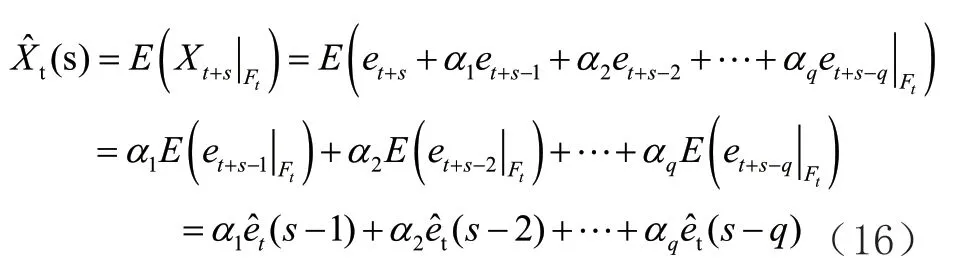

根据式（15）和式（16）,得ARMA(

p

,

q

)模型对销售额时间序列的前

s

步预测方法为（17）：

1.2 多因素影响下基于随机森林（RF）的服装销量预测模型

使用随机森林模型主要采用4 类因素结合起来预测销售额，第一类是节假日数据，第二类是天气数据，第三类是宏观经济数据，第四类是历史销售数据（作为标签）。将这4 类因素进行数据预处理后，得到服装零售数据集。数据集是一个nxm 形式的矩阵，矩阵中的第

n

行代表第

n

个样本，即一条销售记录，矩阵中的前

m

-1 列代表影响销售额的因素，第

m

列为销售额，在该数据集上进行随机森林模型的训练。文章是预测销售额，销售额是一个连续的变量，所以需要通过并行的建立多颗二叉回归决策树(Classification And Regression Tree，CART)，最终对所有决策树叶子节点预测值取平均得到销售额的预测值。单颗二叉决策树的数学原理表达式（18）如下所示：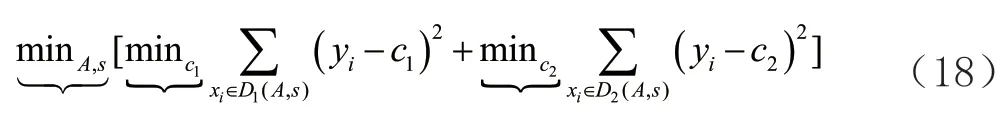

y

是第

i

个样本（销售记录）的真实销售额，

c

为

D

数据集的样本输出均值，

c

为

D

数据集的样本输出均值。为了求出每一次的最优划分特征和最佳划分点，需要采用基尼系数作为划分的依据，基尼系数的表达式（19）如下：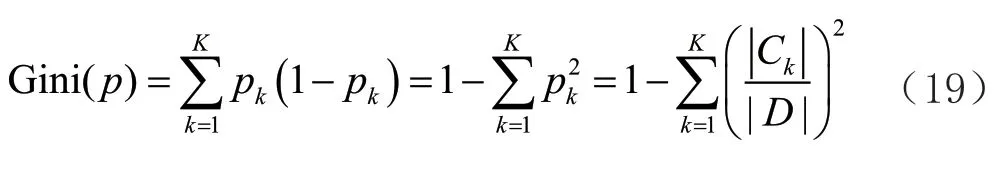

其中，

p

代表样本属于第

k

个类别的概率，|

C

|代表第

k

个类别下的样本量，|

D

|代表总的样本量,基尼系数越接近于0，则划分的效果越好。并行地构造多棵决策树，就得到了随机森林模型。

1.3 组合销售预测模型

ARIMA 模型与随机森林模型训练完毕后，按照如下方式构建组合销售预测模型。首先将时间序列模型

G

的预测误差定义见式（20）：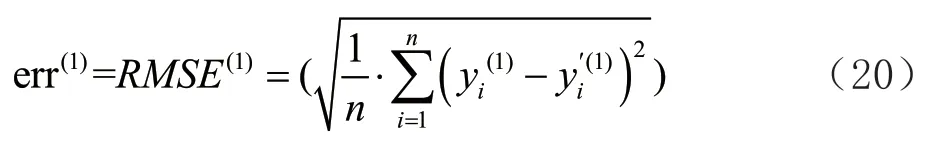

其中，

y

为真实销售额，

y′

为预测的销售额，同理，随机森林模型

RF

的预测误差定义见式（21）：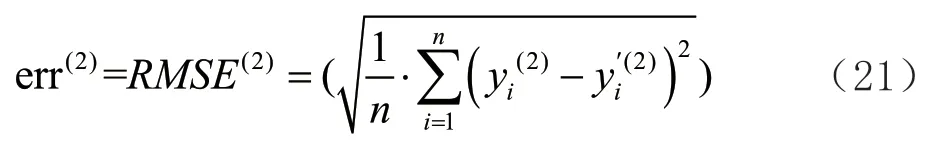

时间序列模型的预测值所占的权重定义见式（22）：

因为模型1 与模型2 的权重之和为1，所以模型2预测出的销售额所占的权重如式（23）所示：

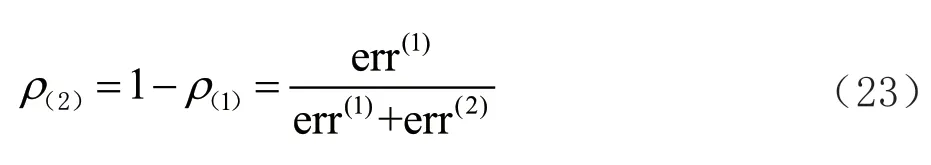
最终得到组合预测模型如式（24）所示：

2 实例分析

为了评估组合销售预测模型的有效性，以机器学习竞赛平台kaggle上所给出的美国某零售商的服装销售数据集为分析对象，按照数据预处理，模型训练，基于交叉验证的参数选择，实例分析模型评估。

2.1 数据预处理

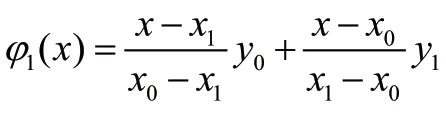
为进一步探究季节性因素对3 种类型服装销售额的影响，需要分别对3 种类型的服装按式（25）求出其季节指数，该指数可同时作为随机森林模型调参的重要依据：

其中

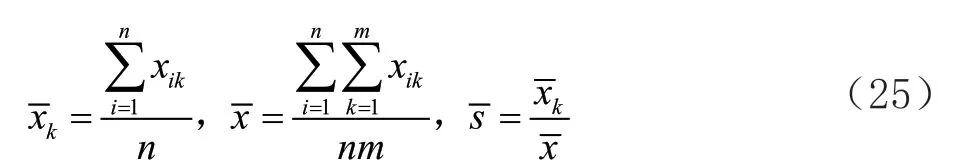
n

为总年数，

m

为总月数，

x

代表第

i

年第

k

月的销售数据，

xk

为周期内各期平均数，

x

-为总平均数，

s

-为季节指数。

对于原始的天气数据，在对缺失值填补后对类别型特征进行哑编码。对于宏观经济数据，删除缺失值数量过多且缺乏有效信息的特征。完成上述处理后，对时间序列值按月进行采样。

2.2 组合预测模型的效果评价

根据式（24）的组合预测模型，笔者以女装为例，以2009—2014 年的销售数据作为训练数据，以2015年的数据作为模型的测试数据，对训练数据作三折交叉验证后，选择均方误差最小的模型及其参数来预测2015 年的销售额，最终求得组合销售预测模型中随机森林模型的权重为0.73，ARIMA 模型的权重为0.27。单一模型以及组合模型的预测效果如图1所示。

图1 单模型以及组合预测模型的预测效果

从图1 中可以看出，ARIMA 与随机森林这两种单一模型都能反映出销售额变化的一些趋势。但ARIMA 仅仅考虑时间因素，所以进行长期预测时偏差很大、权重较小，而随机森林考虑天气、经济等众多因素，预测较为准确，权重更大。组合预测模型结合了这两种模型的优势，在预测效果上能更加接近数据的真实值，偏差相对较小。

3 结语

在大数据时代，服装零售商在进行销售预测时，不仅要考虑历史销售数据，还要获取更多的经济、天气、节假日，甚至消费者习惯等数据。机器学习技术可以充分挖掘和分析数据，准确预测未来消费需求，从而帮助服装零售商做出正确的库存决策。

此外，机器学习往往需要大量的样本参与训练，才能得到鲁棒性强的模型和较高的预测精度，文章中训练随机森林的样本量较少，只有6 年的数据。近年来，发展较快的迁移学习方法可以通过源域到目标域的模型调整，生成大量相似的样本，进而增加数据，提高训练模型的预测精度，这也将是文章进一步研究的方向之一。