灾后煤矿物联网网络空洞覆盖重构算法

胡青松， 范莘舸， 李鹤

（1.中国矿业大学 地下空间智能控制教育部工程研究中心，江苏 徐州 221116；2.中国矿业大学 信息与控制工程学院，江苏 徐州 221116；3.中国矿业大学 徐州市智能安全与应急协同工程研究中心，江苏 徐州 221116；4.徐州燃烧控制研究院有限公司，江苏 徐州 221000）

0 引言

煤矿物联网通过大量节点以自组织方式对井下人、机、环境进行感知[1]。然而，煤矿灾害通常会造成部分节点损坏，形成网络空洞，使得网络拓扑结构变化，可能导致通信中断，使决策指挥者和救援人员无法及时了解灾害现场信息，严重影响应急响应速度和灾后救援效果[2]。鉴于此时仍存在许多残存的物联网节点（简称残存节点）可以工作，若能利用这些节点及救援人员、救援设施携带的通信终端（简称移动节点）重构事故区域物联网[3]，不仅可以修复网络空洞，为不连通的区域提供连通路径，而且可为灾后态势感知及救援工作提供条件。因此，研究灾后环境下煤矿物联网网络空洞的发现和覆盖问题具有重要意义。

网络空洞覆盖问题的主流研究方法是通过增加移动节点进行修复。文献[4]提出了一种基于Voronoi图及Delaunay三角剖分结合的改进虚拟力算法的高效部署策略，运用图论工具定位网络中的覆盖空洞，通过虚拟力移动已部署的节点，但未考虑灾后多障碍物的情况。文献[5]提出了人工势场法，可使移动节点在有障碍物的情况下移动到需要覆盖的地点，但当斥力范围大于障碍物半径时会导致障碍物与移动节点碰撞。文献[6-9]对人工势场法进行改进，提高了移动节点避障能力和移动路径平滑性，减少了规划步数，但仅适用于有单个移动节点的简单环境。文献[10]提出了一种分布式协调策略，适用于有多个移动节点的复杂环境，但节点移动后会出现覆盖率减小或节点停留在障碍物边缘的问题，造成能量浪费。

相比于正常情况，灾后残存节点的能量差异较大，部分残存节点能量可能过早耗尽而影响整个网络的稳定性。现有的网络空洞覆盖算法未考虑井下灾后的地理环境因素，且未对修复后的网络进行优化，无法满足灾后煤矿物联网重构需求。本文提出一种煤矿物联网灾后有障碍物情况下的网络空洞覆盖重构算法（Network Hole Coverage Reconstruction Algorithm with Obstacles, NHCRA−O），提升了节点的匹配收敛速度，缩短了节点移动距离，提升了网络覆盖率，延长了网络寿命，在修复灾后煤矿物联网网络空洞方面具有较大优势。

1 系统建模

1.1 网络模型

本文以煤矿井下局部灾后物联网为研究对象，如图1所示。节点分为残存节点及救援人员携带的移动节点，各节点初始能量可不相同。假定基站和残存节点是静止的，节点数据能以多跳方式传输到基站。各节点通信半径和感知半径均相同，彼此之间可通过接收信号强度值（Received Signal Strength Indicator, RSSI）计算距离。

图1 煤矿井下局部灾后物联网Fig.1 Post-disaster Internet of things in coal mine underground

在网络重构阶段，节点被分为成员节点和簇头节点。成员节点对受灾区域进行动态感知；簇头节点接收成员节点收集的信息，并对其进行压缩和融合处理后传递给下一簇头节点。

为不失一般性，将灾后网络用图模型G=(V,U)表示，其中V为顶点集，U为边集。V由网络中所有节点集合和障碍物角点集合组成[11]。障碍物信息可通过灾后移动节点获取。

1.2 节点感知模型

假定感知范围为以残存节点为圆心、感知半径为r的圆形区域。在网络空洞覆盖问题上，往往由多个残存节点同时感知某一区域，本文采用Neyman−Pearson联合感知模型来计算感知概率[12]。残存节点Si从目标区域k接收到的信号强度为

式中：τ为均值为0、标准差为 σ 的高斯噪声；C0，C1分别为目标区域信号源未丢失和丢失的情况；η为信号源能量；di，k为残存节点Si与目标区域k之间的距离；λ为信号衰减指数，通常取2或4，煤矿灾后场景中一般取4。

式中Einit为残存节点初始能量。

在目标区域信号源未丢失的情况下，残存节点Si的感知概率为

在目标区域信号源丢失情况下，残存节点Si的感知概率为

根据Neyman−Pearson联合感知模型可得，残存节点Si对目标区域k的感知概率为

式中： Φ (·)为标准正态分布累积分布函数；δmin为 最小误警率。

在实际感知过程中，目标区域k可能同时被周围W个残存节点感知，因此，目标区域k的联合感知概率为

当Pk<0.3时，认定该目标区域为空洞区域。

整个网络节点覆盖率为

式中：Acov为所有残存节点覆盖面积；A为所有区域（包含障碍物）面积。

考虑到障碍物的存在，假设c>0.85 时整个监测区域获得有效覆盖，具体取值可调节。

2 灾后煤矿物联网网络空洞覆盖重构

NHCRA−O基本思想：首先，利用Delaunay三角剖分对残存节点及障碍物角点进行区域划分，进而利用节点感知模型判断区域内是否存在网络空洞；其次，计算Delaunay三角形质心位置，利用质心和Delaunay三角形顶点之间的距离确定虚拟修复节点位置；再次，计算移动节点的优先级，并与虚拟修复节点进行可视化判断与匹配，根据匹配结果修复网络空洞；最后，融合剩余能量因子、节点连通度和方向介数计算节点优先级，根据优先级选举簇头节点，其他成员节点就近入簇，形成新的重构网络。

2.1 虚拟修复节点位置确定

以图2所示物联网网络空洞为例进行NHCRA−O说明。S1−S12为残存节点，O1−O4为障碍物角点。S1−S10构成一个网络空洞。由S1−S10，O1−O4构成顶点集V={S1，S2，…，S10，O1，O2，O3，O4}={Vp}（p=1，2，…，14）。

图2 物联网网络空洞Fig.2 Network hole in Internet of things

对V进行Delaunay三角剖分，得到Delaunay三角形修复模型，如图3所示。

图3 Delaunay 三角形修复模型Fig.3 Delaunay triangle repair model

计算Delaunay三角形质心Q的位置（x，y）：

式中（xp，yp）为 Delaunay三角形顶点位置。

计算Delaunay三角形顶点V1与Q的距离dV1,Q。根据三点最优覆盖模型，若dV1,Q大 √于残存节点感知半径r，则在V1与Q连线上距离Q3r处放置修复节点I1，这样可使I1覆盖范围与相邻Delaunay三角形的重叠面积最小，达到最佳覆盖效果。实际放置修复节点时会对其位置做进一步优化，所以这里将I1称为虚拟修复节点。

对Delaunay三角形顶点V2，V3重复上述操作，完成该Delaunay三角形区域空洞覆盖。其他Delaunay三角形空洞区域覆盖过程与此相同。

2.2 基于优先级的双向匹配

通过上述过程可确定虚拟修复节点I的位置。实际用于修复的移动节点M会与其进行匹配，从而确定修复节点最终位置。由于灾后障碍物的存在，虚拟修复节点位置与实际部署位置存在偏差，同时移动节点到达虚拟修复节点位置过程中存在因躲避障碍物导致移动路径过长或无法到达指定位置等问题，需要对虚拟修复节点进行可视化判断。

依次连接障碍物角点，得到一组边集U。若线段与边集U没有交点，则认为该移动节点与虚拟修复节点直接可视，将二者的匹配状态记为可视，反之记为非可视。在匹配过程中，直接可视的移动节点会优先得到虚拟修复节点的匹配邀约，若虚拟修复节点周围无直接可视移动节点，则对非可视节点发出匹配邀约。

虚拟修复节点与移动节点基于双向匹配策略进行匹配。移动节点基于阈值 κ对虚拟修复节点进行匹配优先级排序，κ越大，则优先级越高。

式中：a1，b1为权重因子，a1+b1=1；κ1为虚拟修复节点距障碍物的距离优先级，κ1越小，则虚拟修复节点距离障碍物越近；κ2为虚拟修复节点附近节点剩余能量因子， κ2越小，则对虚拟修复节点的需求度越高，对于灾后井下环境来说，需求度越高，则匹配优先级越高；dI,Om为虚拟修复节点距最近障碍物Om的距离；dmin，dmax分别为网络中虚拟修复节点和障碍物之间的最小距离和最大距离；Ecnow为构成Delaunay三角形的残存节点当前平均能量；Ecavg，Emax，Emin分别为当前网络中残存节点的平均能量、最大能量和最小能量。

虚拟修复节点基于阈值 ω 对移动节点进行匹配优先级排序，ω越大，则优先级越高。

式中：a2，b2为权重因子，a2+b2=1； ω1为移动节点与虚拟修复节点的距离因子， ω1越小，则匹配优先级越高； ω2为移动节点现有能量因子， ω2越大，则匹配优先级越高；dM,I为虚拟修复节点与移动节点的距离；N为当前移动节点可移动范围内的虚拟修复节点数；dM,Ij为当前移动节点与其可移动范围内虚拟修复节点Ij的距离；Emnow为当前移动节点的剩余能量；Emavg，Emmax，Emmin分别为网络中所有移动节点的平均能量、最大能量和最小能量。

本文基于Gale−Shapley算法[13]进行虚拟修复节点与移动节点双向匹配，其是基于稳定匹配策略而设计的贪心算法。1个虚拟修复节点可能会同时向多个移动节点发出匹配邀约，而1个移动节点可能同时收到多个虚拟修复节点的匹配邀约。发出匹配邀约的次数越多，则能耗越大。考虑到灾后节点能量宝贵，对参与双向匹配的节点进行预剪枝处理，即虚拟修复节点根据自身计算的优先级对移动节点进行排序，删除后1/4结果，只对排序前3/4的节点发出匹配邀约。以图4为例，虚拟修复节点I1根据计算的优先级排序删除后1/4数据，向优先级处于前3/4的移动节点M1，M2，M3发出匹配邀约，收到匹配邀约的移动节点根据自身计算结果选择优先级最高的虚拟修复节点进行匹配，从而加快NHCRA−O收敛速度。

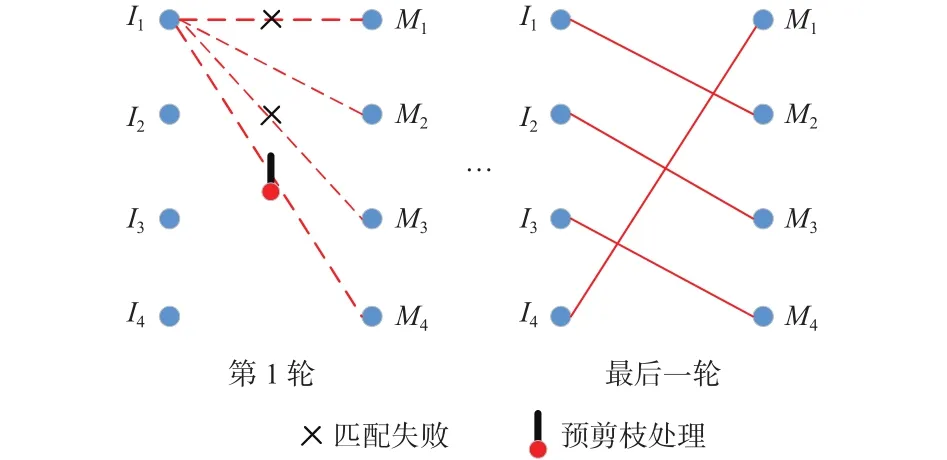
图4 虚拟修复节点与移动节点匹配过程Fig.4 Matching process between virtual repair node and mobile mode

2.3 网络重构

经移动节点修复空洞后的网络仅实现了简单连通，节点位置并非最优，需对其进行重构处理，从而优化网络结构。本文采用层次性网络优化结构，综合剩余能量因子、节点连通度和方向介数计算节点优先级，根据优先级选举簇头节点[14]。

（1） 剩余能量因子。簇头节点将承担更多的数据收发任务，因此应尽量将剩余能量高的节点选为簇头节点。定义剩余能量因子e为当前节点能量Enow与网络中节点能量均值Eavg的比值。

节点剩余能量采用文献[15]中的能耗模型进行计算。

式中：Etx为节点发送数据能耗；l为数据包大小；Eelec为转发大小为l的数据所消耗的能量； εfs，εamp分别为自由空间和多径衰落空间下的功率放大系数；d为收发节点之间的距离；d0为临界距离，Erx为节点接收数据能耗。

dd0时采用多径衰落空间能耗模型。

（2） 节点连通度。为均衡网络能耗，节点密集的区域应增加簇头节点数量，减小簇的规模，而节点稀疏区域则与之相反。定义节点连通度n为邻居节点数Nnei与网络节点总数Ntotal的比值：

（3） 方向介数。方向介数表示某节点通过最短路径到达目标节点的桥接次数，方向介数越大，则该节点承担的收发数据任务越重。

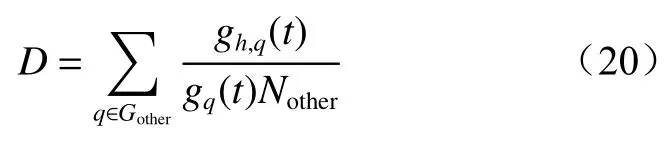
式中：D为节点方向介数；Gother为网络中除目标节点外的其他节点集合；gh,q(t)为t时刻从节点q经过节点h到达目标节点的最短路径数；gq(t)为t时刻从节点q到达目标节点的最短路径数；Nother为网络中除目标节点外其他节点总数。

综合上述3个指标，得到簇头选举优先级：

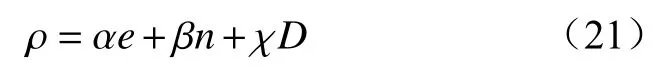
式中 α，β， χ 为权重因子，α + β+χ=1。

节点的 ρ 越大，则当选为簇头的概率越大。完成簇头节点选举后，其他节点依据就近原则加入簇。待网络中所有节点都成为簇头或加入某个簇后，网络重构结束。

3 仿真与结果分析

采用Matlab2016a仿真软件验证NHCRA−O性能。虚拟修复节点和移动节点匹配优先级的权重因子a1=a2=0.6，b1=b2=0.4，簇头选举的权重因子α=0.7，β=χ=0.15，其余参数设置见表1。

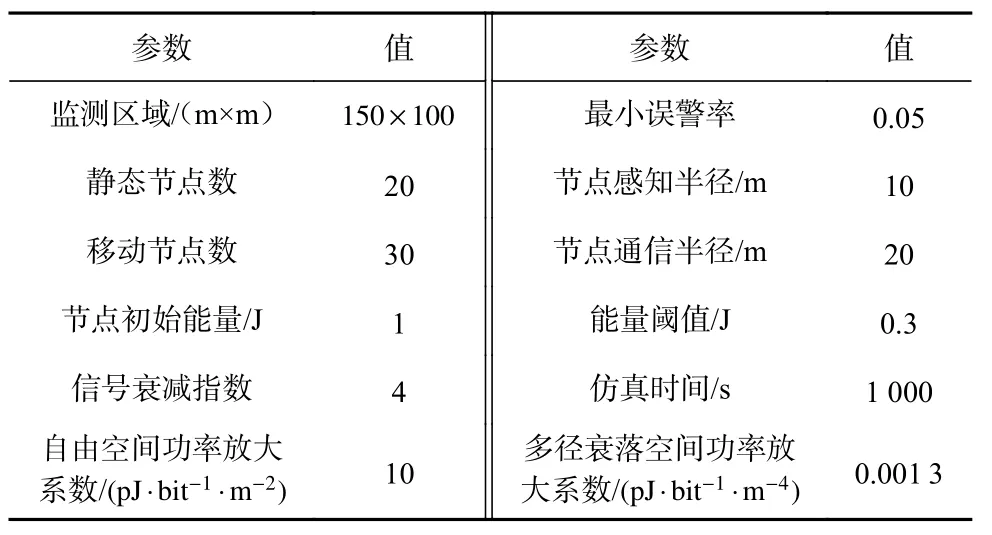
表1 网络空洞覆盖重构仿真参数Table 1 Simulation parameters of network hole coverage and reconstruction

网络空洞修复前后节点位置分布如图5所示，其中多边形区域为障碍物。在障碍物的干扰下，残存节点随机部署形成网络覆盖空洞，通过移动节点进行修复。

图5 网络空洞修复前后节点位置分布Fig.5 Node position distribution before and after network hole repair

NHCRA−O与 Gale−Shapley算法的匹配效率比较如图6所示。可看出Gale−Shapley算法经历86次匹配后完成移动节点与虚拟修复节点的匹配工作，而NHCRA−O只需59次匹配，较Gale−Shapley算法减少31.4%。其原因在于，Gale−Shapley算法是基于稳定匹配策略而设计的贪心算法，而NHCRA−O算法通过可视化判断，基于距离因子和能量因子对虚拟修复节点和移动节点进行双向匹配，同时采用预剪枝处理，剪去了后1/4的匹配数据，从而加快了匹配速度。

图6 虚拟修复节点与移动节点匹配效率Fig.6 Matching efficiency of virtual repair node and mobile node

NHCRA−O 与 C−V 算法[12]、PSO（Particle Swarm Optimization，粒子群优化）算法[16]的网络覆盖效率对比如图7所示。从图7（a）可看出，NHCRA−O网络覆盖率随移动节点的增多而迅速提升，原因是其通过Delaunay三角剖分锁定网络空洞区域，并利用双向匹配策略为网络空洞选取最优修复节点。当移动节点超过25个时，网络覆盖率趋于稳定，约为90%。C−V算法和PSO算法需要35个移动节点才能使覆盖率进入稳定状态。此外，无论是算法执行过程中还是稳定状态下，NHCRA−O的网络覆盖率均大于其他2种算法。从图7（b）可看出，NHCRA−O的节点平均移动距离明显小于其他2种算法，这归功于NHCRA−O进行了可视化判断，并基于能量因子和距离因子挑选最优修复节点。

图7 网络覆盖效率对比Fig.7 Comparison of network coverage efficiency

重构网络的生存时间随节点数量变化情况如图8 所示。可看出与 SEP（Sequential Exchange Protocol，按先后顺序交换）算法[14]、LEACH（Low Energy Adaptive Clustering Hierarchy）算法[15]相比，经NHCRA−O修复空洞后，网络生存时间明显高于其他2种算法，原因在于NHCRA−O不但直接将剩余能量考虑在内，还考虑了网络连通情况和方向介数，从而大幅提高了网络寿命。

图8 网络生存时间对比Fig.8 Comparison of network time-to-live

4 结论

（1） 针对灾后煤矿物联网因节点损毁和障碍物遮挡出现的网络空洞问题，提出了NHCRA−O。该算法通过可视化判断与双向匹配策略，对虚拟修复节点和移动节点进行匹配，并引入剩余能量因子、节点连通度及方向介数对修复后的网络进行重构。

（2） 采用 Matlab2016a 软件进行仿真实验，结果表明NHCRA−O在匹配效率、网络覆盖效率和网络生存时间等方面均表现出良好的性能。

（3） 在后续研究中，计划将 NHCRA−O 与灾后实测数据采集融合，研发可修复网络空洞和重构网络的救灾机器人，用于指导矿井灾害救援实践。