基于SOGI-FLL-WPF的磁悬浮多跨转子不对中振动检测

关旭东 ，周 瑾 ，金超武 ，姚润晖

（1.常州大学机械与轨道交通学院，江苏 常州 213164；2.南京航空航天大学直升机传动技术重点实验室，江苏南京 210016；3.南京航空航天大学机电学院，江苏 南京 210016）

随着旋转机械往高速、柔性、大功率方向发展，逐渐出现附带联轴器连接的多跨转子系统，多跨转子系统存在诸多需要解决的关键问题.转子不对中故障会造成转子振动位移与基座振动力中出现二倍频成分，联轴器的特性也直接影响转子的运行状态.当旋转机械运行中出现由转子不对中引起的异常，轻则停机、中断生产过程、降低工作效率，重则产生转子与机壳间的碰摩或出现失稳现象，导致设备破坏，甚至造成严重的事故.

联轴器与轴承支承组件对转子系统乃至整个机械设备的动力学特性起到关键作用[1].对转子不对中来说，传统轴承支承的多跨转子系统一旦设计加工，较难进行不对中量的在线调整.转子不对中故障是旋转机械运行中常见故障之一，研究发现转子不对中故障占转子故障的60%以上[2].转子对中是指两个或多个转子通过联轴器连接后，转子的轴线重合.对中后的转子在运行过程中，不会出现转速的二倍频成分，这对减小转子振动及机体振动起到关键作用.转子不对中主要包括联轴器不对中和轴承不对中，本文主要研究前者，其主要分为平行不对中、偏角不对中及平行与偏角复合不对中3种形式[3].

目前，国内外在传统多跨转子不对中的动力学模型建立、故障辨识与振动控制方面，已开展了相关研究工作[4-7].针对多跨转子系统有限元模型自由度较多问题，研究者提出结合固定界面模态综合法的降维增量谐波平衡法，从而保证计算精度与效率[8].文献[9]采用有限元法，发现挠性联轴器不对中会使转子位移谐波分量增大.李明等[10]基于油膜轴承多跨转子实验台，分析了联轴器不对中时转子运动规律，表现为二倍及多倍频谐波较多.黄志伟等[11]通过分岔图、庞加莱截面图、轴心轨迹图和时域波形图等，系统地分析了发电机转子与水轮机转子在耦合故障下非线性动力学响应.在多跨转子故障方面，学者分析了不对中、碰摩、裂纹等故障类型，分别通过离线分析[12]与有限元法[13]辨识故障.在多跨转子过临界转速方面，通过在线控制转子动力吸振器中电磁铁的吸合状态，实现转子较小的振动水平[14].磁悬浮多跨转子系统是将传统轴承支承方式替换为主动磁悬浮轴承（active magnetic bearing, AMB）支承，在磁悬浮多跨转子不对中方面，王金健等[15]针对多跨转子多频传递力，提出一种变步长神经网络算法.Bouaziz等[16]采用Newmark方法对磁悬浮轴承系统进行仿真，研究了磁悬浮多跨转子不对中的动态特性，结果表明，角度偏差使得二倍和四倍运行速度分量占主导地位，且大小随磁悬浮轴承中电磁铁的数量和定子与转子间的气隙而变化.Kuppa等[17]采用磁悬浮轴承抑制由于不平衡和不对中产生的过大振动，采用反馈控制器调节磁悬浮轴承的控制电流，提出了一种量化方法评估磁悬浮轴承的动态特性.

本文针对磁悬浮多跨转子不对中振动检测问题，提出基于带预滤波器的二阶广义积分-锁频环（second order generalized integrator-frequency locked loop with prefilter，SOGI-FLL-WPF）磁悬浮多跨转子不对中振动检测新方法，为磁悬浮多跨转子不对中振动控制奠定基础.

1 磁悬浮多跨转子系统

磁悬浮多跨转子平台如图1所示，包括径向磁悬浮轴承、轴向磁悬浮轴承、转子、联轴器、电涡流位移传感器、电机等.联轴器两端转子由磁悬浮轴承支承，两转子由联轴器连接，联轴器右端磁悬浮轴承不仅起到支承转子作用，还可充当电磁激振器，为多跨转子系统提供激振力，从而实现多跨转子系统的模型辨识.利用磁悬浮轴承系统本身配备的信号采集与控制系统获得转子振动响应数据，并结合本文提出的转子不对中检测方法，可实现多跨转子不对中振动的检测.

图1 磁悬浮多跨转子平台示意Fig.1 Schematic diagram of magnetic suspension multi-span rotors platform

2 刚性转子四自由度动力学模型

如图2所示，刚性转子在空间有6个自由度（degree of freedom, DOF），分别为沿x、y、z轴的3个平动及 3个转动.图中：xsa（xsb）为 A 端（B 端）传感器检测转子沿x轴方向的位移；ysa（ysb）为A端（B端）传感器检测转子沿y轴方向的位移；xba（xbb）为A端（B端）磁悬浮轴承处对应转子沿x轴方向位移；yba（ybb）为A端（B端）磁悬浮轴承处对应转子沿y轴方向位移；（xc，yc，zc）为转子质心C在空间的坐标；s1（s2）为 A端（B端）传感器在z轴方向的坐标值，其中s1＜ 0；a（b）为 A 端（B 端）磁悬浮轴承在z轴方向的坐标值，a＜ 0；α、β分别为绕x、y轴的欧拉角；转子绕z轴旋转且转速为Ω.对于磁悬浮轴承转子系统，电机带动转子绕z轴转动，磁悬浮轴承系统则需要控制其余5个自由度.忽略径向与轴向的耦合，建立径向四自由度磁悬浮轴承转子系统动力学模型.

图2 四自由度磁悬浮轴承转子系统动力学模型Fig.2 Dynamic model of 4-DOF magnetic bearing rotor system

根据刚体动量矩定理与动量定理，可推导出转子的动力学方程为

式中：Jz为转子绕z轴的转动惯量；J为转子绕x、y轴的转动惯量；m为转子质量；fax（fbx）为 A端（B端）磁悬浮轴承对转子在x方向的电磁力；fay（fby）为A端（B端）磁悬浮轴承对转子在y方向的电磁力.

将式（1）写成矩阵形式：

式中：M为广义质量矩阵；G为陀螺矩阵；B和C均为系数矩阵；q为转子模型质心坐标及欧拉角的合成矢量；qs为位移矢量；u为电磁力矢量.上述矩阵分别表示为

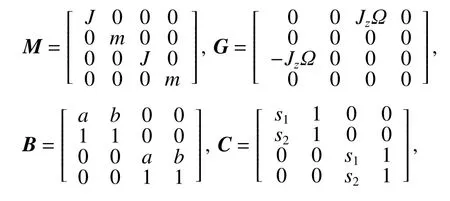
将AMB的电磁力线性化为

式中：Ks和Ki分别为位移刚度系数矩阵和电流刚度系数矩阵；qb为磁悬浮轴承处对应转子位移矢量；i为电流矢量；kx和ki分别为位移刚度系数和电流刚度系数；iax（ibx）为 A 端（B 端）磁悬浮轴承在x轴方向上的线圈电流，iay（iby）为 A端（B端）磁悬浮轴承在y轴方向上的线圈电流.

因此，可以得到AMB支承的刚性转子的运动微分方程为

当引入不平衡质量时，转子的运动方程（式（1））改写为

式中：mu为不平衡质量；u为转子的不平衡偏心距，即不平衡质量质心到z轴的垂直距离；zu为不平衡质量质心的z坐标； φ0为不平衡位置角.

3 联轴器不对中模型

多跨转子不对中时，联轴器受力示意如图3所示.图中：F为半联轴器的受力；O1为主动转子中心线；O2为从动转子中心线；d为主动转子与从动转子间的平行不对中量；过O1向O2N做垂线交于点G.两转子由两个半联轴器连接，两转子以角速度Ω旋转，经过时间t转过Ωt角度.以联轴器上一点N为两半联轴器的连接点，转子旋转时，O1N受压，O2N受拉.

图3 多跨转子联轴器受力Fig.3 Stress diagram of coupling in multi-span rotors system

由于d≪，则可近似认为，两半联轴器的总变形量为

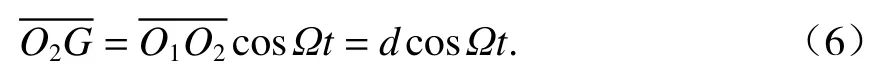
因此，半联轴器的受力为

式中：K为半联轴器刚度.

将式（7）所示的力分别投影至水平方向和竖直方向，得出对应分力Fx与Fy分别为

综上所述，由于联轴器不对中引起作用于磁悬浮轴承转子上的径向力[18]为

由式（10）可知，联轴器不对中导致频率为转子转速二倍频的旋转力，其大小与d成正比.

根据式（5）、（10）建立附带联轴器作用的磁悬浮轴承转子四自由度刚性数学模型.磁悬浮轴承控制器均采用PID控制，功率放大器数学模型由实验拟合得到，传感器数学模型视为比例增益.通过上述建立的仿真模型既可以模拟转子旋转状态，又可以对转子施加联轴器作用力，仿真参数如表1.

表1 仿真参数Tab.1 Simulation parameters

4 多跨转子不对中振动检测方法

磁悬浮多跨转子不对中振动控制的实施需要以不对中振动检测为基础，因此，本文结合二阶广义积分-锁频环（second order generalized integratorfrequency locked loop, SOGI-FLL）展开转子不对中振动检测方法研究.

4.1 归一化SOGI-FLL

在SOGI中，通过在一个单位反馈结构中使用双积分器结构来提取单相输入信号的基频分量及其正交成分，如图4所示，该结构通常也被称为二阶广义积分正交信号发生器（SOGI-based quadrature signal generator, SOGI-QSG），图中：v为输入信号；vs为输入信号v的同步分量；qvs为vs的正交值；γ0、k为放大器增益；ev为误差信号；ω0为给定的信号频率.SOGI-QSG的两个典型传递函数D(s)和Q(s)分别为

图4 归一化SOGI-FLL原理Fig.4 Principle of normalized SOGI-FLL

式中：Vs(s)、V(s)和Qvs(s) 分别为vs、v和qvs的象函数；s为复频率.

对于给定的正弦输入信号v=Vsin(ω0t+φ)，利用图4中的结构可推导出vs和qvs.因此，SOGIQSG可生成输入信号的同步信号与正交信号.

由式（11）、（12）可知，D(s)和Q(s)分别为以谐振频率ω0为中心频率的带通滤波器和低通滤波器，且带通滤波器的带宽仅由k决定，与中心频率ω0无关，低通滤波器的增益同样仅取决于k.通过设置不同的k，获得D(s)和Q(s)传递函数的Bode图如图5所示，由图可知：增益k对两个滤波器的频率响应的影响是显而易见的；输出vs在ω0处与输入v不存在相位滞后，且幅值增益为0 dB，即实现了一比一跟踪；输出qvs在ω0处与输入v存在90°相位滞后，且幅值增益为0 dB，即产生了输入的正交量.

图5 不同k值下SOGI滤波器的Bode图Fig.5 Bode diagram of SOGI filter under different k

由输入信号v至误差信号ev的传递函数E(s)为

式中：Ev(s) 为ev的象函数.

E(s)为通用陷波器的表达形式，本文后续滤除转速同频分量时将会采用SOGI的形式.

4.2 SOGI-FLL-WPF频率估计原理

当待检测信号中存在直流偏置或谐波干扰时，SOGI-FLL频率估计方法的抑制干扰能力会变弱，此时，估计信息会有波动甚至出错.文献[19]提出将基于SOGI的滤波器作为先前结构的预滤波器，得出了一种简单的新型结构，该结构被称为带预滤波器的SOGI-FLL，即SOGI-FLL-WPF，其控制原理如图6所示.图中：v0为预滤波器输入信号；k0、k1为阻尼系数.

图6 SOGI-FLL-WPF的控制原理Fig.6 Control principal of SOGI-FLL-WPF

两个SOGI的级联结构可以解决qvs输出中的低频扰动、直流偏置和谐波等扰动问题，其控制思路包括两个SOGI结构的串联.第一个用作带通前置滤波器，第二个是幅值与频率归一化的SOGI-FLL，它可以获取输入信号的估计频率.

对2个SOGI级联的研究可以扩展到n个SOGI的级联，如图7所示.对于相同的阻尼因子，n阶系统比单个SOGI可获得更高的谐波衰减和相似的稳定时间.该系统的两个典型传递函数为

图7 n个SOGI的级联Fig.7 Cascade diagram of n SOGIs

式中：Vsn(s) 和Qvsn(s) 分别为第n阶SOGI系统同步分量vsn和正交分量qvsn的象函数.

减少n阶SOGI稳定时间的方法是增大系统的阻尼系数，即增大系数k，但要以降低谐波衰减为代价.可以逐渐适当地增加这些阻尼因子，从而获得与单个SOGI相同的谐波衰减.在这种情况下，n阶SOGI的稳定时间比单个SOGI的稳定时间快.因此，n阶SOGI可以实现比单个SOGI更快的瞬态响应，且具有相似的谐波衰减.SOGI级联的阶数越高，对待检测信号的高阶谐波衰减也越大.

5 多跨转子不对中振动检测仿真验证

5.1 多跨转子不对中振动检测方法

图8为基于转子径向位移信号的转子不对中振动检测原理框图.由于不平衡质量的存在，转子在旋转过程中，其径向振动位移信号中主要包括转速同频分量.当转子不对中振动发生时，转速二倍频的不对中振动信号和转速同频信号混叠在一起.基于转子径向位移信号的转子不对中振动检测方法为：首先，采集转子径向位移信号；然后，利用归一化SOGI-FLL进行转子转速估计；接着，将估计的转速信息反馈给SOGI进行自适应同频陷波，以滤除径向位移信号中转速同频分量，从而获得仅受转子不对中振动影响的位移信号；最后，利用SOGI-FLLWPF对上述滤除转速同频干扰后的径向位移信号进行转子不对中振动检测.

图8 基于径向位移信号的转子不对中振动检测原理Fig.8 Schematic diagram of rotor misalignment vibration detection based on radial displacement signal

5.2 定转速与变转速下多跨转子不对中振动检测

引入转子不对中力模型后，仿真计算得到如图9所示的转子运行状态图.本文磁悬浮轴承系统中位移传感器检测电压为0 ～ 5 V，对应的转子实际位移为0 ～ 0.25 mm，因此，检测转子不对中量与电压值的对应关系为20 000 V/m.

由图9可以看出：引入模拟转子不对中后，转子的轴心轨迹由圆形变成不规则的圆形，由于转速二倍频的存在，导致轴心轨迹趋于“三角形”；转子两端的振动位移均处于ISO 14 839[20]定义的限制区域A中.

图9 转速为6 000 r/min下转子运行状态Fig.9 Running state of rotor at 6 000 r/min

以转子A端x轴方向为例，采集转子该方向位移信号并进行快速傅里叶变换（fast Fourier transform,FFT），得到如图10所示结果.由图10可以看出：转子振动位移主要包括两个频率信号，其中100 Hz为转子旋转频率，200 Hz则是由于转子不对中引起的二倍频信号.

图10 转速为6 000 r/min下转子位移信号频谱Fig.10 Spectrum for displacement signal of rotor at 6 000 r/min

为了验证检测方法的有效性，结合磁悬浮轴承转子模型并引入转子不对中量，对转子振动信号进行实时分析，得到如图11所示的检测结果.由图可以看出：转子陷波后振动信号仅有二倍频分量；依据SOGI-FLL实时辨识得到的转子转速信号，转子在第1.00 s时开始旋转，此后一直在该转速下运行，转速辨识与设定转速误差几乎为0，可准确地对转子转速进行辨识，该信号为陷波同频量的依据；转子位移信号中滤除转速同频量后依据SOGI-FLLWPF可准确检测出转子不对中振动.

图11 转速为6 000 r/min下转子不对中振动检测结果Fig.11 Misalignment vibration detection results of rotor at 6 000 r/min

针对图11（a）中转子位移信号进行频谱分析得到如图12所示的结果，通过对比可以看出：转子陷波后转速同频量被完全滤除，此时转子位移信号中仅存在转子转速二倍频分量.

图12 滤波前后转子振动位移频谱对比Fig.12 Spectrum comparison of rotor vibration displacement before and after filtering

为了进一步验证升速过程中转子不对中检测效果，设定转子升速由100 Hz开始以6 Hz/s逐渐升速至112 Hz，得到如图13所示的变转速下转子不对中检测结果.由图可知：在转子升速过程中，本文提出的基于SOGI-FLL-WPF的磁悬浮多跨转子不对中振动检测方法仍然具有较好的效果.

图13 升速过程中转子不对中振动检测结果Fig.13 Misalignment vibration detection results during rotor acceleration

6 多跨转子不对中振动检测实验验证

为了验证本文提出的磁悬浮多跨转子不对中振动检测方法的效果，采用磁悬浮四自由度多跨转子实验台进行转子不对中振动检测实验验证.实验台如图14所示，将电机底座通过垫片抬高使电机转子与磁悬浮轴承转子具有一定的不对中量.磁悬浮转子悬浮并通过电机使其旋转至1 200 r/min.此时多跨转子处于不对中的工作状态，采集转子振动位移信号并进行不对中振动检测检测，得到如图15所示检测结果.

图14 磁悬浮四自由度多跨转子实验台Fig.14 Test rig of magnetic suspended 4-DOF multi-span rotors

在图15中分别给出了采用归一化SOGI-FLL和归一化SOGI-FLL-WPF进行转子不对中振动检测的对比效果.在第1.00 s时刻，辨识转子转速模块启动后约0.05 s可以获得转子转速频率约为20 Hz，与设定转子转速频率一致.通过对比可以看出：采用归一化SOGI-FLL-WPF可以获得更好的检测效果，在打开检测开关后约0.10 s检测结果便趋于稳定状态，不对中振动的频率约为40 Hz，即转子转速的二倍频，不对中振动的幅值约为0.03 V.

针对图15（a）中转子位移信号进行频谱分析得到如图16所示的结果，通过对比可以看出：转子陷波后转速同频量几乎被完全滤除，此时转子位移信号中仅存在较大的转子转速二倍频分量及其他较小的转子转速倍频分量.

图15 磁悬浮多跨转子不对中振动检测结果Fig.15 Detection results for misalignment vibration of magnetic multi-span rotors

图16 滤波前后转子振动位移频谱对比Fig.16 Spectrum comparison of rotor vibration displacement before and after filtering

在转子不对中状态下，将其运行状态绘制于图17中.由图可明显看出：转子运行的轴心轨迹变得不规则，说明振动位移信号中已经包含了由转子不对中引起的转速二倍频信号.

图17 转子不对中状态下的运行状态Fig.17 Operation state of rotor under misalignment

7 结 论

1） 依据转子径向振动位移信号，利用SOGIFLL可实现转子转速辨识，为转速同频量陷波提供前提条件.

2） 结合转子转速辨识结果，并利用SOGI对转子径向位移信号进行转速同频陷波，然后采用SOGI-FLL-WPF对陷波后位移信号进行不对中振动检测.通过模拟定转速和变转速两种工况验证了本文提出磁悬浮多跨转子不对中振动检测方法的可行性.

3） 通过实验验证了本文提出的磁悬浮多跨转子不对中振动检测方法的效果，实验结果表明，采用本文提出的检测方法，在打开检测开关后约0.10 s检测结果便趋于稳定状态，由转子不对中引起的转速二倍频振动信号可被快速辨识出幅值和频率.

今后可以针对磁悬浮多跨转子偏角不对中、平行与偏角复合不对中进行不对中振动的检测研究，提出一套识别不同类型多跨转子不对中振动的检测方法，为后续磁悬浮多跨转子不对中振动控制奠定基础.

致谢：常州大学科技计划项目（ZMF21020019）、直升机传动技术重点实验室基金（HTL-A-20K03）的资助.