磁力涡旋压缩机永磁随变机构的力学特性

史 策 ，徐方超 ，孙 凤 ，金俊杰 ，佟 玲 ，周 庆 ，张晓友 ,2

（1.沈阳工业大学机械工程学院，辽宁 沈阳 110870；2.日本工业大学机械工学科，日本 埼玉 345-8501）

涡旋压缩机通过动静涡旋盘的涡旋齿相互啮合压缩气体，这对于涡旋型线的加工精度有很高的要求；若精度不够，在动静涡旋所形成的压缩腔内将发生气体泄漏，导致涡旋压缩机工作效果达不到预期要求[1].对此，国内外学者进行了深入的研究.文献[2]从涡旋盘受力分析和运动轨迹的角度研究了径向随变机构对涡旋压缩机的泄漏与密封的影响，揭示了随变机构的工作原理和工作规律.文献[3]研究了径向随变机构对涡旋压缩机转子系平衡的影响，针对偏心套筒式径向随变机构引起的涡旋压缩机转子系平衡破坏的问题，依据其工作原理和受力模型，研究涡盘发生偏移时惯性力对偏移程度及轴承承载能力的影响.文献[4]将动涡盘设计成轴向随变结构，在动涡盘下端安装弹簧和平衡块使其能沿着曲轴轴向滑动.文献[5]设计了一种涡旋槽式轴向随变机构，建立了更适合描述涡旋槽的随体坐标系，描述涡旋压缩机所在柱坐标系和随变机构坐标系的关系，搭建涡旋槽模型实验平台，并分析了在不同转速下涡旋槽的流量和进出压力的变化，研究随变机构对涡旋压缩机压缩气体的影响.文献[6]提出了一种轴向随变机构，通过轴向随变机构保持最佳间隙来控制泄漏，通过数值计算优化结构设计，并制造样机进行测试，研究轴向随变机构对涡旋压缩机在低速运行时减少泄漏的情况.关于随变机构以往的研究多是对涡旋压缩机工作性能的作用和影响，提出的随变机构都需要机械接触和润滑，对需要洁净气体的环境并不合适.

磁悬浮技术可以实现非接触驱动，具有很好的发展前景，一直是国内外学者的研究热点.文献[7-9]介绍了磁悬浮轴承的结构和工作原理，建立悬浮力的数学模型，运用有限元法分析并进行实验研究.文献[10-12]对混合磁轴承进行设计和分析，建立数学模型，分析磁轴承径向自由度之间的耦合以及径向自由度与轴向自由度之间的耦合，最后采用有限元仿真，验证了数学模型的正确性.文献[13-14]运用虚位移法研究了磁弹簧的数学模型，分析磁环的尺寸对磁力的影响，并用实验验证了结果.文献[15-17]针对永磁悬浮系统的悬浮力非线性变化的特点进行研究，介绍磁路结构和工作原理，基于磁力刚度和位移建立数学模型，通过有限元法对磁力模型进行验证，并提出控制方法.

上述文献研究了磁悬浮技术的工作原理和应用.磁悬浮机构可以避免摩擦和撞击，适合应用在无油涡旋压缩机中[18-19].首先，本文根据磁力涡旋压缩机的结构特点提出了永磁随变机构，采用虚位移法建立磁力的数学模型，计算径向磁力和轴向磁力，分析磁力与位移的关系.然后，采用理论公式、有限元仿真和实验分析永磁随变机构工作气隙处的磁感应强度.最后，研究永磁随变机构的工作性能与磁环尺寸参数和位移的关系.

1 结构和工作原理

1.1 磁力涡旋压缩机的结构和工作原理

磁力驱动无油涡旋压缩机的结构如图1所示，主要由动涡盘、静涡盘、电磁铁、衔铁、磁环、传感器、磁铁座组成，3组电磁铁两两相对，每组电磁铁都配有一个电涡流传感器.工作原理为3组电磁铁吸引衔铁和动涡盘实现轨迹运动，从而进行气体压缩.为使涡旋压缩机工作中有一定的刚度，每组电磁铁采用差动控制.Y方向的传感器测量衔铁的位置，X方向的2个传感器测量衔铁的位置和旋转角度，通过实时检测与控制，使X方向的2个传感器距离保持始终相等，确保动涡盘的平动运动，代替了防自转机构的使用，进而减少摩擦，实现无油运行.如图1（b）所示，该涡旋压缩机在轴向为被动悬浮，永磁随变机构安装在衔铁下面，由4组永磁环组成，分别安装在磁铁架下面的4个凹槽里呈对称分布，上下互为相斥.在轴向方向，随变机构提供的轴向磁力大于压缩机产生的最大气体力，具有较好的刚度.当涡旋压缩机受到撞击或震动时，永磁随变机构将进行柔性抵抗，动涡盘迅速回到原位.涡旋压缩机工作时，每组磁环的径向距离为涡旋压缩机的回转半径，径向相斥抑制压缩机的气体泄漏，当动涡盘遇到由于加工误差形成的凸点或强烈振动时会自动避让.

图1 涡旋压缩机结构Fig.1 Scroll compressor structure

1.2 永磁随变机构调节原理

涡旋压缩机的工作原理是动涡盘行走特定轨迹，并始终与静涡盘啮合压缩气体.实际中，由于加工误差和工作时振动等情况，涡盘之间无法保持刚好啮合的状态，随变机构可以解决此问题.

永磁随变机构轴向偏移示意如图2所示.图中：h为涡盘齿高； φ 为动涡盘发生偏移时上端面与静涡盘的夹角.永磁随变机构工作原理如图3所示，图中红色涡旋为运动中的动涡盘，蓝色圆环为动静涡盘正常运行时的啮合轨迹，所遇凸点半径r0为

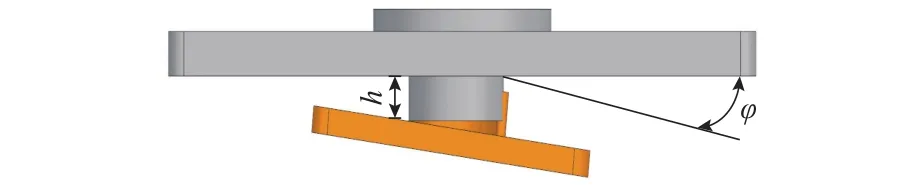
图2 永磁随变机构轴向偏移示意Fig.2 Axial offset of permanent magnet variable mechanism

图3 永磁随变机构工作原理Fig.3 Working principle of permanent magnetic compliance mechanism

式中：ex和ey分别为当动静涡盘在啮合处遇到固体颗粒时动涡盘在X和Y方向的退让距离.

涡旋压缩机实际工作时的工作半径为

式中：（xm，ym）为给定的涡旋压缩机的运行轨迹.

当动涡盘与静涡盘啮合时遇到凸点会自动避让，动涡盘避让后轨迹半径变小，此时永磁随变机构斥力变小，绕过凸点后动涡盘迅速增加位移填补缝隙与静涡盘继续啮合.此时轨迹半径变大，永磁随变机构径向斥力变大，永磁随变机构的径向磁力始终垂直于行走轨迹，有利于减少径向缝隙从而减少泄漏.当磁力驱动涡旋压缩机遭到撞击发生振动，永磁随变机构对动涡盘起到缓冲作用.

2 永磁随变机构的数学模型

2.1 磁力模型

磁环磁极之间的磁导[14]如式（3）所示.

式中：Gg为气隙处的磁导；g为两个磁环中心的距离；μ0为空气磁导率；R为外环半径；r为内环半径；m为磁环左右移动的距离；n为上下两磁环的垂直距离.

式中：W为气隙磁能； φg为磁环总磁通；Kr为径向经验补充系数；Ka为轴向经验补充系数.

2.2 磁感应强度分析

为控制磁力涡旋压缩机运行提供更加真实的数据，采用理论计算分析永磁随变机构的性能，并对磁环的径向磁场强度进行有限元仿真和实验验证.实验台由刻度尺、探头和螺旋测微器组成.磁环内环半径 5 mm，磁环外半径10 mm，高度3 mm.

径向气隙磁感应强度为

式中：Br永磁体的剩余磁感应强度；Sm为永磁体中磁路的横截面积；Sg为气隙处的横截面积；Ki为磁路i的漏磁补充系数.

磁环的径向磁感应强度的理论计算、有限元仿真和实验对比结果如图4所示.由图可知：磁感应强度的理论计算值与实验结果的平均绝对值误差为3.08 mT，相对平均误差9%；有限元仿真与实验结果的平均绝对值误差为3.6 mT，相对平均误差25%.有限元仿真结果与实验相差较大，其原因是磁环中心的磁感应强度的方向并不是完全向上，磁环左右充磁不均匀.

图4 磁环的径向磁感应强度Fig.4 Radial magnetic induction intensity of magnetic ring

径向磁感应强度分布如图5所示.由图可知：磁环内圆磁场方向与磁环端面磁场方向相反，磁感线由内圆出发向进入磁环端面.磁感应强度在两个磁环的外环相邻处最大，故磁环的径向外延处的磁力最大.

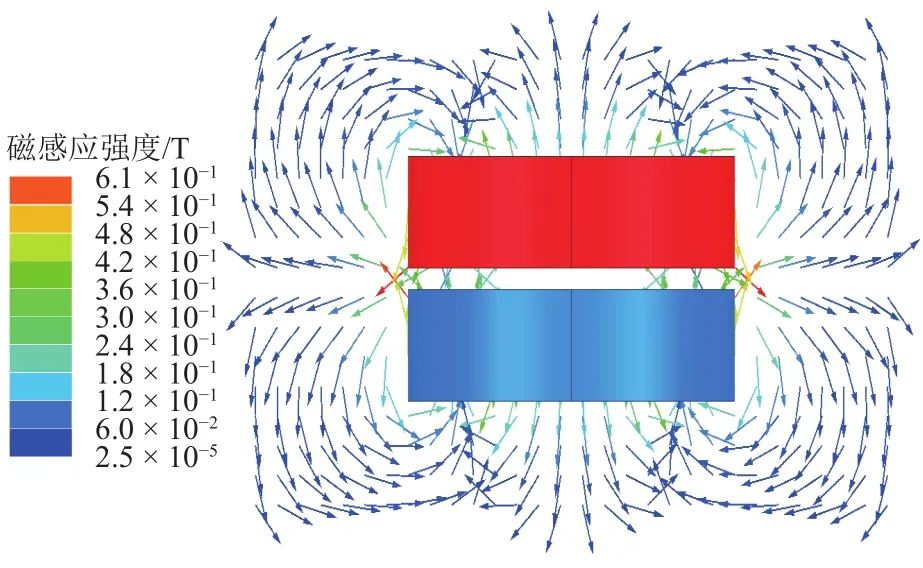
图5 径向磁感应强度分布Fig.5 Radial magnetic induction intensity distribution

3 永磁随变机构的尺寸特性仿真分析

永磁随变机构的参数如图6所示，H1为永磁环的高度.仿真参数如下：永磁环剩磁Br= 0.857 T，永磁环矫顽力Hc= -653 000 A/m.

图6 永磁随变机构的结构参数Fig.6 Structural parameters of permanent magnetic compliance mechanism

3.1 径向力和轴向力与磁环内圆半径的关系

磁环的外径尺寸不变，高度不变，上下磁环径向距离为1 mm，轴向距离0.5 mm.理论计算和有限元分析径向力、轴向力与磁环内圆半径的关系如图7所示.由图可知：随着内圆半径由3 mm增加到5 mm，轴向力和径向力逐渐变大；内圆半径从5 mm增加到7 mm时，轴向力和径向力逐渐变小.半径3 mm时，内圆空间小，仅有少部分磁感线在内圆附近，故磁力较小，随内圆半径增加，磁环内圆的侧面的磁能作用增加，故磁力变大；内圆半径从5 mm增加到7 mm时，磁环的内圆变大磁环质量变小，磁能变小，故磁力变小.

图7 径向磁力和轴向磁力与磁环内径的关系Fig.7 Relationship between radial magnetic force, axial magnetic force and inner diameter of magnetic ring

3.2 径向力和轴向力与磁环高度的关系

理论计算和有限元分析径向力、轴向力与磁环高度的关系如图8所示.当磁环的内外径尺寸不变，磁环高度增加，轴向磁力和径向磁力都随之增加，但是径向磁力增加很小.涡旋压缩机最大的气体阻力为轴向压力，由此可见，增加磁环高度可以有效增加永磁随变机构的背压能力.与理论计算的结果相比，磁环轴向磁力的有限元仿真数值随磁环高度变化的增长率先高后低，说明磁环的磁力随高度的实际变化并不是线性增加，随高度的增加到一定值后磁力增加缓慢.

图8 径向磁力和轴向磁力与磁环高度的关系Fig.8 Relationship between radial magnetic force, axial magnetic force and height of magnetic ring

3.3 径向力和轴向力与轴向位移的关系

磁环的内外径尺寸不变，上、下磁环径向距离为1 mm，理论计算和有限元分析径向力、轴向力与轴向位移的关系如图9所示.轴向距离从0.5 mm增加到6.0 mm，磁环的轴向磁力和径向磁力都随轴向位移增加而减少.为保证永磁随变机构具有较高的斥力，以起到背压的作用，磁环间的轴向距离尽可能小，但为保证实际加工精度和装配精度允许，故采取0.5 mm的轴向距离.

图9 径向磁力和轴向磁力与轴向位移的关系Fig.9 Relationship between radial magnetic force, axial magnetic force and axial displacement

4 永磁随变机构磁力特性验证

4.1 磁力驱动涡旋压缩机性能参数

磁力驱动无油涡旋压缩机应用在医疗洁净环境，为病人输送氧气，设计为低压比，转速为1 200 r/min.气体压力与旋转角的关系和型线参数分别如图10和表1所示，以此作为永磁随变机构尺寸参数的优化依据.图中，θ为排气角.永磁随变机构所能提供的磁力需大于涡旋压缩机产生的最大气体力，满足涡旋压缩机的运行，磁环的尺寸决定了磁力的大小，在满足压缩机的需要的基础上，尺寸不宜过大.气体力计算是在传统公式上乘以经验泄露系数得到的[20].

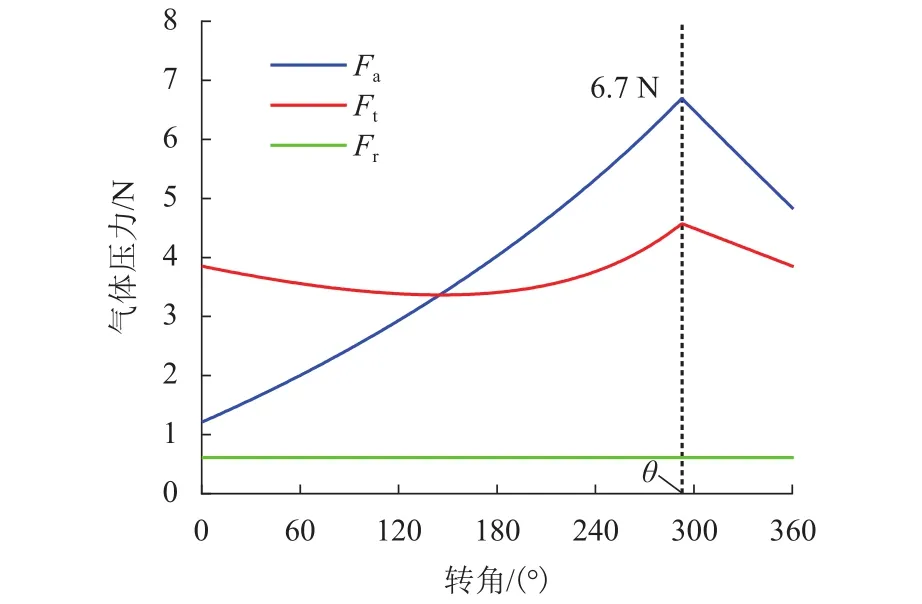
图10 气体压力与旋转角的关系Fig.10 Relationship between gas pressure and rotation angle

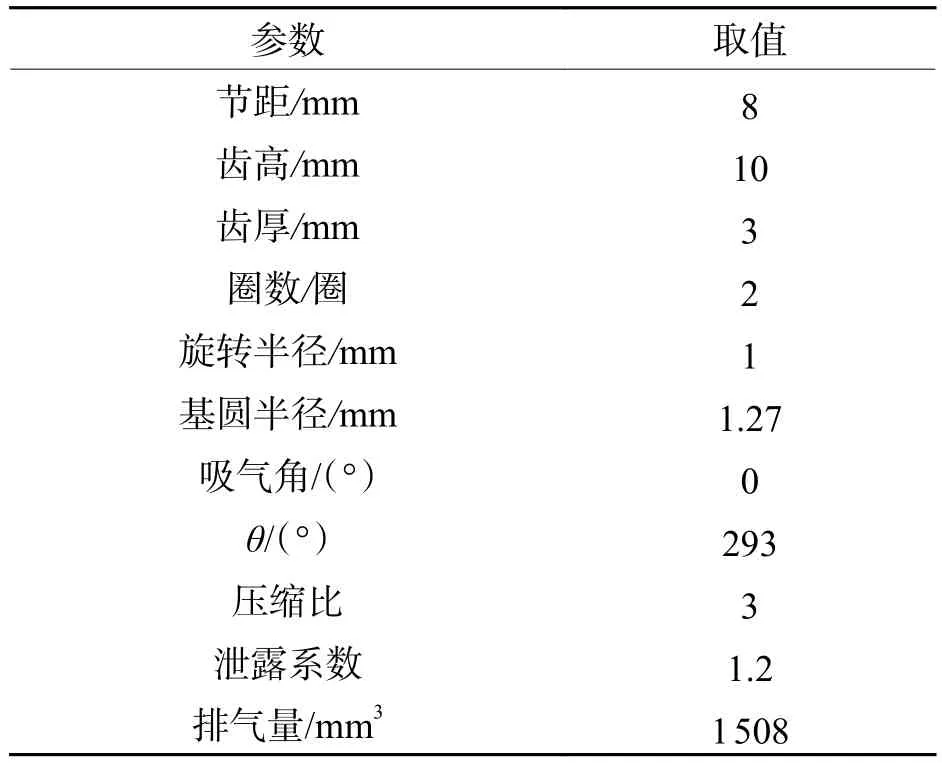
表1 压缩机型线参数Tab.1 Parameters of scroll compressor profile

4.2 永磁环磁力特性的实验对比

轴向磁力测试实验台由测力传感器、螺旋测微器、移动台所组成.测力传感器型号Load Cell CXZ-114，量程为0至300 N，精度为 0.01 N，螺旋测微器的量程为13 mm，分度值为 0.01 mm，两自由度的移动台的量程为 13 mm，分度值为 0.01 mm，磁环内环半径5 mm，磁环外半径10 mm，高度3 mm.

轴向磁力与径向位移关系如图11所示.轴向磁力随径向距离增大而减小，有限元仿真与实验结果相近，平均绝对值误差为0.72 N，相对平均误差5.8%.径向磁力与径向位移关系如图12所示.径向磁力随磁环径向位移的增加而增加，径向磁力的理论计算与实验结果的平均绝对值误差为0.35 N，相对平均误差为10%；仿真结果与实验的平均绝对值误差为0.26 N，相对平均误差为13.6%.

图11 轴向磁力与径向位移关系Fig.11 Relationship between axial magnetic force and radial displacement

图12 径向磁力与径向位移关系Fig.12 Relationship between radial magnetic force and radial displacement

动涡盘的行走轨迹为半径为1 mm的圆，动静涡盘始终啮合，此时永磁随变机构具有相对较高的斥力，增加系统刚性.实验测得，永磁随变机构工作距离内单组磁环的最小轴向力为8.73 N，在工作轨迹上的径向力为4.8 N，满足磁力涡旋压缩机的工作需求.径向磁力与径向位移近似呈线性关系，磁环向水平各个方向移动相同距离产生的径向磁力相同，即等刚度.

5 结 论

1） 提出一种永磁随变机构用于磁力涡旋压缩机，设计了永磁随变机构的结构并分析其工作原理.

2） 采用虚位移法计算磁力模型，并结合有限元仿真和实验对永磁随变机构进行对比研究.永磁随变机构的径向磁力在一定范围内随着径向位移的增加而增加，随着轴向位移的增大而减小.径向位移与永磁随变机构刚度系数近似呈线性关系.永磁随变机构在平动平面内各个移动方向的刚度系数相等.

3） 在工作距离内永磁随变机构单组磁环的最小轴向磁力为8.73 N，在工作轨迹上的径向力为4.8 N，满足磁力涡旋压缩机的工作需求.