基于LabVIEW的时域抽样定理仿真实验

杨 敏，秦传波，曹 路，李澄非

（五邑大学 智能制造学部，广东 江门 529020）

0 引言

抽样定理是信号处理、通信系统等的基础，是进行模拟信号向数字信号转换的必要步骤，是 “信号与系统” 课程教学的重要知识点之一。只有深刻理解抽样定理才能确切明白模拟信号为什么可以转换成数字信号来进行传输、处理，然后在有需要的条件下又可以恢复原始模拟信号。抽样定理的推导并不复杂，国内外经典教材［1-5］都有详细的理论讲解和公式推导。但是地方性高校二年级学生数学基础较为薄弱，普遍缺乏学习的韧劲，动手能力也略有欠缺，课堂上单纯的理论讲解和公式推导会让学生感觉枯燥，学习缺乏积极性，为提高教学质量，让学生充满学习的动力，提高学生动手能力，在课内外采取何种手段使学生能够深入透彻地理解和应用抽样定理，是教师目前教学的难点。

杨巧宁等［6］采取问题法、案例法、图形演示法和实践法等多种教学方法对抽样定理课堂教学进行分析。尚影等［7］运用Matlab软件来仿真来实现信号抽样，并在图形界面上显示相应结果。李蓉艳等［8］通过Multisim软件仿真电路，Analog Discovery2口袋仪器搭建实际电路，实现了抽样定理的创新性实验。栗学丽［9］实现了基于LabVIEW的频域抽样定理的实验研究。

LabVIEW是图形化编程软件，编程实现容易，界面按照各自要求定制，可直观显示各种信号图形，显示直观。本文实现了基于LabVIEW的时域抽样定理仿真实验，通过图形化显示帮助同学们理解和使用时域抽样定理，掌握频率混叠等相关概念。

1 时域抽样定理

时域抽样定理：一个频谱在区间(-ωm，ωm）以外为零的有限频带信号f(t），可唯一地由其在均匀时间间隔上的抽样值f(nTs）所确定［1-5］。

时域抽样定理表明，为了能从抽样信号f s(t）不失真地完全恢复原信号f(t），必须满足两个条件：(1）信号f(t）必须是频带受限信号，其频谱在｜ω｜＞ωm时为零；(2）抽样频率不能过低，必须ωs≥2ωm(或f s≥2f m），或者说抽样间隔不能太大，必须若不满足这两个条件，则抽样信号f s(t）的频谱将会出现频谱混叠现象。

2 时域抽样定理仿真界面设计

实现抽样定理的仿真，需要能显示原始带限信号波形图和频谱图、抽样后信号波形图和频谱图，用户通过改变输入信号频率、幅度和抽样信号频率等观察不同频率抽样信号作用下抽样后信号的时域图和频谱图，并据此判断是否混叠。时域抽样定理仿真整体界面如图1所示。

图1 时域抽样定理仿真界面

左上角可设置原始信号的参数。包括可选信号类型，默认单频正弦波，除此之外可选三角波、方波、锯齿波；包括信号的相位、偏移量等都可以设置。当然同学们也可以在上述版本基础上自行编程实现其他信号作为输入信号。左下角显示原始信号和抽样信号频率之比以及显示是否混叠。右边有两个波形图，分别显示原始信号和抽样后信号的时域波形和频谱。中间是设置原始信号的频率和采样信号频率。

3 时域抽样定理程序框图及验证

通过LabVIEW编程实现时域抽样定理，主要功能包括基本信号的生成、傅立叶变换、抽样实现、波形显示和频谱显示等。

3.1 时域抽样定理程序

整体程序如图2所示，主要使用了基本函数发生器、重抽样、FFT变换、波形图等子VI。通过基本函数发生器子VI，可以配置原始信号波形种类、信号频率、幅度、初始相位、偏移等物理量。原始信号波形输入波形重采样子VI，以采样频率重采样后获得抽样后信号。上述两种信号经过组合直接送入波形图分两通道显示时域波形。上述两种信号分别送入FFT频谱子集子VI，进行时域-频域转换，获得FFT变换后的幅度和相位，送入波形图中分两通道显示幅度谱。同时对采样频率和原始信号频率做对比，如果比值大于2则显示不混叠，如果比值小于或者等于2则显示混叠。

3.2 时域抽样定理验证

图1和图3、图4分别显示了f s＞2f m、f s=2f m、f s＜2f m时仿真的结果。图1中，原始信号频率是4 Hz，采样信号频率是20 Hz，频率之比明显大于2。采样后信号波形逼近原有正弦波，频谱基本一致，频谱未发生混叠，容易通过滤波器从抽样后信号恢复出原始信号。图3中，原始信号频率为5 Hz，采样信号频率是10 Hz，频率之比为2，即原有信号中每个周期采样2个点，如图2所示。若在0时刻开始采样，刚好所有采样点的幅度都是0，是一条直线，是无法恢复原始信号；如果不在0时刻开始采样，虽然采样点幅度不会都为0，但是明显样本数量不够，也无法恢复原始信号。图4中，原始信号频率为5 Hz，采样信号频率是8 Hz，频率之比为1.6，小于2，频谱发生混叠，采样后信号频率如图所示为3 Hz，即原始信号5 Hz经过采样信号频谱搬移后变成3 Hz。即高频信号变为低频信号，无法从采样后信号中通过滤波器恢复出原始信号。

图2 时域抽样程序

图3 f s=2 f m时示例界面

图4 f s＜2 f m时示例界面

在课堂讲解抽样定理时，一般会演示给同学们看上述抽样定理的仿真实验，同时会将源程序共享给学生，以便学生课后自行研究和扩展相关功能。在如图1所示教师版本仿真界面上，学生通可过选择不同输入信号，调整输入信号频率、采样信号频率等，可以非常直观地观察原始信号的波形，抽样后信号的波形以及各自频谱图形，深刻理解抽样中混叠的概念。

同时学生可以仿照教师版本仿真程序自己编程，扩展上述程序功能。如图5所示为某班级学生在教师版本基础上扩展了相关的程序，得到的结果。从程序和界面上看，输入信号不再仅仅局限于单频信号，而是上述单频信号之和，如图5所示，原始信号为两个单独正弦波之和，两个正弦波频率分别为10 Hz和13 Hz，幅度分别为2和1；上述两个正弦波之和的最大频率13 Hz，采样频率设置为16 Hz，因此不满足抽样定理的条件。经计算可知抽样后信号频率为：

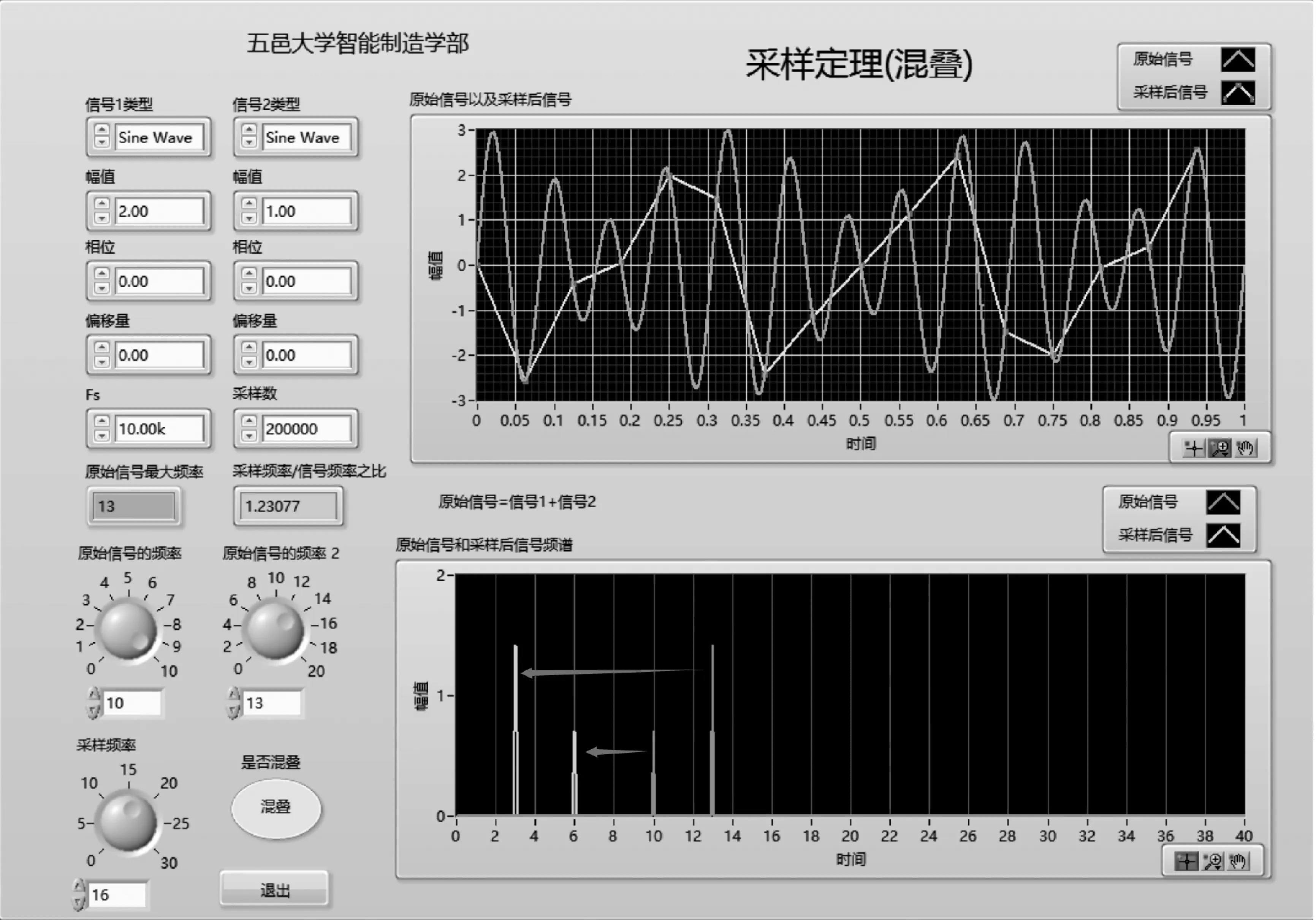
图5 学生扩展后的实验

观察图5中的右下角频谱图，图形所显示与计算结果相符合。

目前在本校进行教学的班级在教学过程中都会演示上述仿真，同时鼓励同学们课后开展实验验证，开发不同类型信号的验证性实验，比如有些同学考虑输入语音信号进行抽样定理验证，有些同学采用振动信号进行抽样定理的验证，还有些同学在仿真的基础上考虑进行硬件的设计和实施，种种手段不一而足。

4 结语

数据采集是信息时代相关技术的基础，而抽样定理是数据采集的基础。通过LabVIEW实现时域抽样定理的仿真实验能有效地帮助学生理解和使用抽样定理，激发学习 “信号与系统” 等相关课程的兴趣，鼓励他们对信号处理等相关理论知识进行仿真探索研究，提高动手能力，为后续知识打下坚实基础，同时做到理论与实践相辅相成，共同进步。