大型钢网架穹顶结构弹塑性稳定性分析

张洋 陈朝晖 杨帅

摘 要：針对大型LNG储罐钢网架穹顶结构的弹塑性稳定性分析，基于刚体准则与改进塑性铰模型建立适于几何与材料双非线性分析的空间弹塑性梁单元，研究局部荷载扰动与整体模态扰动两种不同的初始缺陷处理方法以及材料非线性对结构稳定承载力影响的差异。结果表明：初始缺陷、材料非线性与约束刚度减小均会降低网架穹顶结构稳定承载力;荷载干扰下，结构稳定承载力对干扰大小敏感而对位置不敏感;模态干扰属于整体几何缺陷，结构整体初始变形较大，荷载位移曲线平滑。与ABAQUS相比，所建的弹塑性刚体准则空间梁单元及其相应的非线性分析方法效率与精度兼优，适用于大型复杂工程结构非线性分析，在处理局部缺陷对结构稳定性的影响上具有优势。

关键词：网架穹顶;弹塑性;几何非线性;刚体准则;增量迭代法

中图分类号：TU311.4 文献标志码：A 文章编号：2096-6717（2022）05-0189-08

收稿日期：2020-09-06

基金项目：国家自然科学基金（51678091）

作者简介：张洋（1996- ），男，主要从事结构非线性分析研究，E-mail：zxyoung@live.com。

陈朝晖（通信作者），女，教授，博士生导师，E-mail：zhaohuic@cqu.edu.cn。

Received：2020-09-06

Foundation item：National Natural Science Foundation of China （No. 51678091）

Author brief：ZHANG Yang （1996- ）， main research interest： structural nonlinear analysis， E-mail： zxyoung@live.com.

CHEN Zhaohui （corresponding author）， professor， doctorial supervisor， E-mail： zhaohuic@cqu.edu.cn.

Elasto-plastic stability analysis of large steel grid dome structure

ZHANG Yang， CHEN Zhaohui， YANG Shuai

（a. School of Civil Engineering; b. Key Laboratory of New Technology for Construction of Cities in Mountain Area， Ministry of Education， Chongqing University， Chongqing 400045， P. R. China）

Abstract：Based on the rigid body rule， an improved plastic hinge model is adopted to produce a spatial elasto-plastic beam element for the stability analysis of the steel dome structure of LNG storage tank by the consideration of the nonlinearity of geometry and materials.Two different methods of considering initial imperfections between local load disturbance and global modal disturbance and whether to consider the influence of material nonlinearity on the stability of the structure are studied. The results show that the initial defects， material nonlinearity and reduction of restraint stiffness will all reduce the stable bearing capacity of the grid dome structure. The stable bearing capacity of the structure under load interference is sensitive to the magnitude of the interference but not to the position; the modal interference is an overall geometric defect， the overall initial deformation of the structure is large， and the load-displacement curve is smooth.Compared with ABAQUS， the elasto-plastic rigid body criterion spatial beam element and its corresponding nonlinear analysis method are more efficient and accurate. It is suitable for nonlinear analysis of large and complex engineering structures， and has advantages in dealing with the effects of local defects on the structural stability.

Keywords：grid dome; elasto-plasticity; geometric nonlinearity; rigid body rule; incremental-iterative method

大型LNG储罐的钢穹顶通常采用单层球面钢网壳结构，加上表面钢筋混凝土后，结构自重近万吨。既有结构分析表明，LNG储罐钢穹顶在穹顶混凝土浇筑过程中存在整体失稳的可能性，其安全性由整体稳定性控制。由于其结构跨度大、结构体系较柔，具有强几何非线性的特性。此外，在空间钢网架穹顶结构受力过程中，钢材可能发生屈服，因此，LNG储罐稳定承载力分析需考虑几何与材料的双重非线性效应。常规屈曲分析主要采用模态干扰，需要先求解结构初始模态，再乘以系数作为结构整体初始位移缺陷，这种分析方法计算量大，也不能反映结构局部缺陷的影响。

结构非线性分析常用方法包括完全拉格朗日列式（TL列式）、更新拉格朗日列式（UL列式）和协同转动格式（CR列式）等，Bathe等提出的空间梁单元UL列式应用较为广泛。UL列式和CR列式考虑了结构构形的变化，其对空间框架结构大变形的描述更为方便，但需减小荷载步增量或增加单元划分数才可获得较高的精度，计算效率较低;对于柔性结构，计算结果可能不合理。Yang等指出，对于满足平衡的单元，如果发生刚体位移，其平衡的结点力将随单元刚体转动而改变方向，但大小不变，单元在当前状态仍然平衡，这就是几何非线性分析的“刚体准则”。Yang等、陈朝晖等根据这一准则建立了一系列单元，包括适用于柔性空间框架结构材料几何双非线性分析的集中塑性铰弹塑性平面和空间梁单元，以及与刚体准则相匹配的UL列式非线性增量迭代方法。在增量分析全过程中，基于刚体准则的单元始终满足平衡条件。因此，该方法具有对局部荷载或内力变化的天然敏感性，这也是目前常用的其他大变形非线性分析单元及方法不具备的特点。

笔者针对大型LNG储罐钢网架穹顶结构，基于刚体准则，结合改进集中塑性铰模型的空间弹塑性梁单元及其相应的非线性增量迭代法，采用局部荷载扰动与整体模态扰动方法研究初始缺陷对结构稳定承载力的影响。其中，局部荷载扰动用以模拟网架局部缺陷，从而探究网架结构稳定性对局部缺陷大小及位置的敏感程度。通过与ABAQUS计算结果对比，验证方法的效率、精度及工程适用性。

1 弹塑性与几何非线性增量迭代法

1.1 集中塑性铰模型

如图1所示，在满足刚体准则的弹性空间梁单元两端加入集中塑性铰弹簧，设单元其余部分仍为弹性，则可建立基于刚体准则的弹塑性空间梁单元。

式中：EI/L为梁的弯曲线刚度，当杆端截面完全屈服、弹簧刚度为0时，截面形成塑性铰。当单元结点处于弹性状态时，塑性铰弹簧刚度无穷大，笔者取S=10×（EI/L）。杆件弹性段的几何刚度在截面屈服过程中不受影响。

1.2 弹塑性非线性单元刚度矩阵

根据刚体准则，结构从初始平衡状态到当前变形状态的大变形或大位移可分解为两个过程：首先，单元发生刚体位移，初始平衡状态的单元结点力随单元发生平移和转动，大小不变;随后，在当前位置发生有限变形，可为弹性变形或非弹性变形，变形引起的单元结点力增量可由单元弹性刚度矩阵或弹塑性刚度矩阵得到。对于工程中的绝大多数大变形和大转动问题，可以认为，相较于有限变形，刚体位移占绝大部分，如图2所示的压杆屈曲就可视为这种情形。由这一简化假定而产生的对实际变形的描述误差可通过细分单元或减小步长来降低。

结合前述集中塑性铰模型，基于UL列式，可推导刚体准则弹塑性空间梁单元的刚度矩阵。可知，当梁端截面完全屈服时，截面弯矩增量为0，即

在單元发生刚体转动时，建立的弹塑性刚度矩阵单元虚应变能为零，不会产生结点力增量。式中k为单元弹性段的几何刚度矩阵，满足刚体准则，详见文献[11]。

1.3 基于刚体准则的增量迭代法

基于UL列式的非线性分析增量迭代法包括3个步骤，即位移增量预测、结点力计算和误差判断。其中，位移增量预测是在给定荷载增量下计算结构整体结点位移增量，是结构全局分析。

设第i增量步、第j迭代步的结构整体增量平衡方程可写作

kΔU=λ+R（12）

R=P-F（13）

式中：k为结构刚度矩阵;ΔU为结构位移增量;P、F和R分别为荷载向量、节点内力向量和结点不平衡力。

单元结点力计算是以当前状态为参考，计算单元节点力增量。可由结构位移增量ΔU提取单元节点位移向量u，根据刚体准则，单元结点力为上一迭代步的结点力做刚体转动至单元当前位置后再叠加弹塑性变形产生的结点力增量，计算式为

f=f+Δf=f+ku（14）

式中：Δf为单元弹塑性变形产生的结点力增量。f、f分别为当前迭代步和上一迭代步的节点内力向量。

误差判断用以计算并判断结点不平衡力是否满足收敛要求。通过组集单元结点内力得到结构结点内力向量F。由式（13）计算当前迭代步的结点不平衡力，若满足收敛条件，则进入下一增量步;否则，继续进行位移预测和单元结点力计算直至收敛。可见，单元结点力增量的计算对几何非线性分析的精度起决定作用，该部分造成的不平衡误差无法通过迭代根本消除。

采用上述方法编写相应程序，进行空间柔性网架结构屈曲分析。其中，荷载增量因子λ采用了Yang等提出的广义位移控制法，该方法具有自适应性、计算效率高的优点，在静力和动力非线性分析中获得了广泛应用。

2 钢网架穹顶结构弹塑性稳定性分析

2.1 算例概况

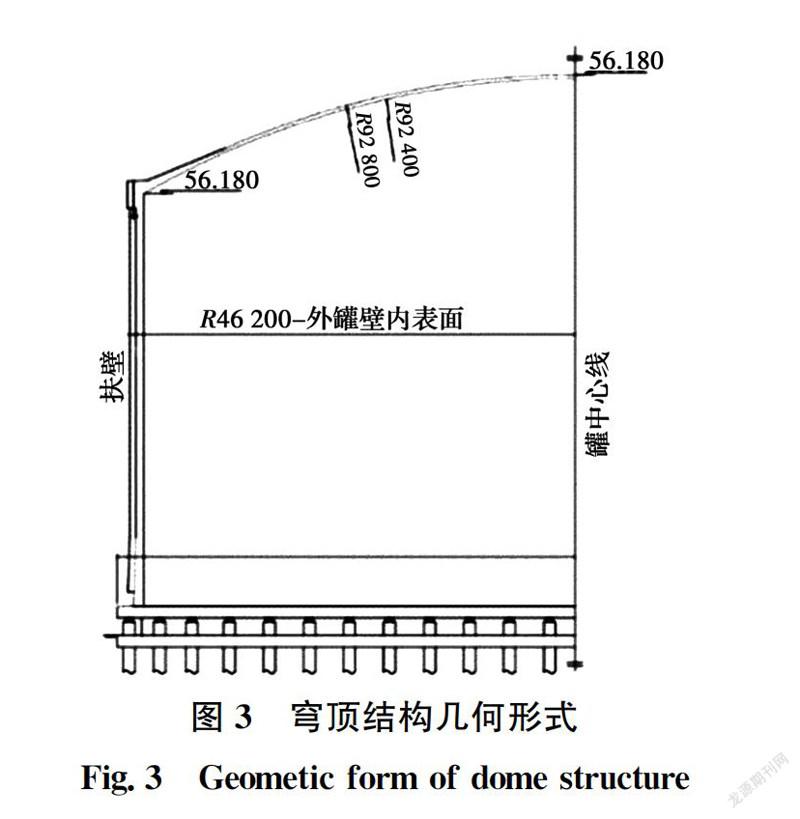
某22万m LNG储罐的钢穹顶如图3所示，由圆柱壳罐体及球壳穹顶组成，跨度92.4 m，钢穹顶与外罐连接处标高43 m，顶部标高55.78 m，曲率半径92.4 m。LNG储罐的钢穹顶由钢板与H型钢梁焊接组成，其中，钢板采用16MnDr（Q345）钢材，厚6 mm;径、环向梁均采用Q345钢材。径向梁为窄翼缘工字型钢HN400×200×8×13（半径2.25～36.45 m）和HN400×400×13×21（半径36.45～46.2 m）;环向梁为窄翼缘工字型钢HN400×200×8×13。该结构的材料参数见表1。

不考虑穹顶蒙皮钢板与网架的共同作用，将荷载静力等效转化为沿网架径向梁的等效线荷载。LNG储罐钢穹顶与外罐连接方式通常为焊接，实际约束介于固定支座与铰支座之间，故分别考虑固定支座与铰支座两种情形。采用前述刚体准则空间弹塑性梁单元进行钢穹顶屈曲分析，并与弹性空间梁单元和ABAQUS对比。

Morris研究表明，结构整体缺陷可使稳定性临界荷载下降35%。因此，结构稳定性分析应考虑初始缺陷的影响，采用几何缺陷和荷载干扰两种方式施加初始缺陷。其中，几何初始缺陷选取网壳的一阶屈曲模态且缺陷变形处最大计算值取为网壳跨度的1/300，即0.308 m;荷载干扰则采用随机对某节点施加微小干擾力的方法来实现。

采用所建刚体准则塑性铰空间梁单元，每根杆件划分2个单元，共计2 598个。同时，采用ABAQUS中的B32OS单元进行对比，每根杆件划分4个单元，在穹顶中心区域局部加密，内圈径、环向梁每根杆件划分16个单元，次内圈径、环向梁每根杆件划分8个单元，共计8 460个。定义材料为理想弹塑性，屈服强度取345 MPa。B32OS单元每个结点7个自由度，包含考虑工字型截面翘曲影响的自由度。取初始荷载为0，荷载增量为1 kN/m，荷载增量因子初值为1。

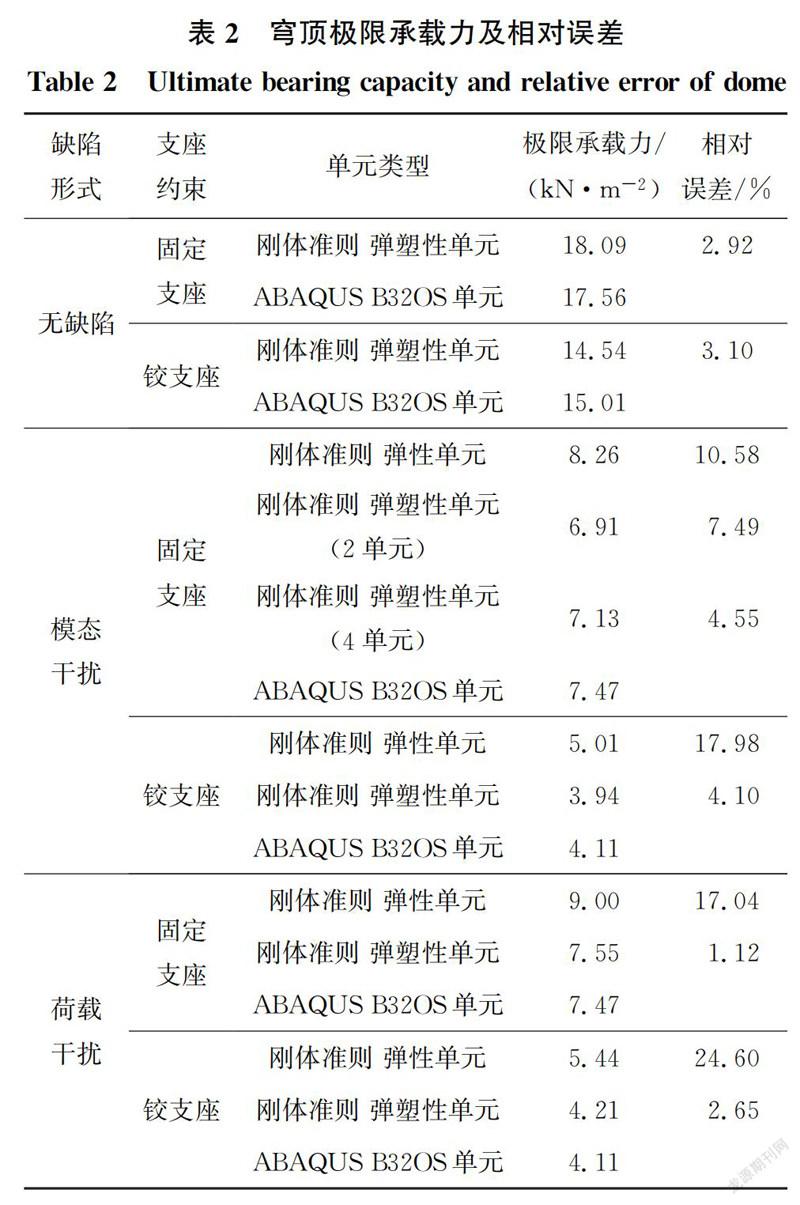
分别施加模态干扰和荷载干扰，其中，模态干扰为整体几何缺陷，而荷载干扰为局部缺陷，以此对比结构整体缺陷与局部缺陷对其稳定性的影响。采用弹塑性空间梁单元进行穹顶结构屈曲和后屈曲分析，网架穹顶结构的荷载与顶点竖向位移曲线如图4所示，图中给出了其与无初始缺陷、弹性屈曲分析以及ABAQUS计算结果的对比。可见，采用建立的弹塑性空间梁单元与ABAQUS结果高度吻合。表2为网架穹顶结构的极限承载力以及与ABAQUS计算结果的相对误差。施加局部荷载扰动时，该方法所得承载力与ABAQUS相差仅1.1%，后屈曲分析曲线基本重合。参照ABAQUS，弹性屈曲分析的平均误差为17.55%，而考虑了材料非线性的弹塑性屈曲分析的平均误差仅为3.84%。可见，针对受到几何与材料双重非线性影响的大型LNG储罐钢穹顶结构进行稳定性分析时，弹塑性屈曲分析具有重要性和必要性。

受局部荷载干扰时，在固定支座和铰支座下，刚体准则单元与ABAQUS结构均吻合良好;施加几何缺陷时，铰支座下本文单元与ABAQUS结果吻合良好，而固定支座下相差7.49%，相对较大，这可能是由于固定支座下薄壁型钢截面翘曲加剧，而本文单元未引入翘曲自由度。为此，将每根杆件划分为4个单元，共计5 196个单元，仍小于ABAQUS单元数，则穹顶结构的极限承载力相对误差降为4.55%。可见，基于刚体准则的单元可以通过增加单元数来考虑截面复杂变形的影响而无需增加结点自由度或假设复杂的单元变形曲线。

本文单元数不到ABAQUS的1/3，且单元的几何刚度矩阵为线性矩阵，弹塑性分析为集中塑性铰模型，单元构造简单。所采用的基于刚体准则的单元未对杆件屈曲模式进行人为假定，满足刚体运动中的平衡条件，因此，此类单元在迭代计算的收敛效率与精度上具有天然优势，且对荷载扰动敏感，可采用局部荷载扰动进行结构屈曲分析。笔者在空间拱结构屈曲分析中对刚体准则单元的这一优势也有论述。

图4还显示，支座固定时，有初始几何缺陷的钢穹顶结构弹塑性屈曲承载力（6.91 kN/m）远小于无初始缺陷的情形（18.09 kN/m），显然，初始缺陷显著影响了钢穹顶的整体稳定承载力。此外，对应固定支座和铰支座，钢穹顶的极限承载力分别为6.91、3.94 kN/m，网架结构稳定性对支座约束条件敏感。图5为钢穹顶的屈曲变形图，可见，在考虑初始缺陷以及几何与材料双重非线性的影响下，钢穹顶的失稳模式为局部区域凹陷。

3 钢网架穹顶结构稳定性参数分析

针对该钢网架穹顶结构，对比荷载干扰与初始几何缺陷下的稳定性。

固定支座下，在网架穹顶中心顶点处施加竖向干扰力，分别为原荷载的1/1 000、1/200、1/100、1/20和1/10，改变初始几何缺陷大小，以一阶屈曲模态为基准且其缺陷变形最大值分别取为0.1Δ、0.25Δ、0.5Δ、0.75Δ和1.0Δ，Δ=0.308 m，进行钢穹顶非线性全过程分析。

由图6所示的穹顶中心荷载位移曲线可知，初始缺陷的选取会显著影响钢穹顶的稳定承载力。其中，受到荷载干扰的结构初始变形较小，在极值点附近突变;而具有几何缺陷的结构初始变形相对较大，荷载位移曲线较为平滑。

在网壳穹顶中心顶点处和半径为2.25、7.34、12.405、17.415、22.365 m的变形最大节点及其对称节点共11个不同位置分别施加竖向干扰力，大小均为原荷载的1/10，得到的穹顶中心荷载位移曲线如图7所示，可见，在不同节点位置施加干扰力得到的结果一致，即穹顶结构对荷载干扰位置不敏感。

结构稳定荷载与初始缺陷大小的关系如图8所示，荷载干扰和几何缺陷导致整体稳定承载力相对于无初始缺陷的下降率分别为53.22%、57.05%、58.29%、59.77%、61.06%和61.99%、63.20%、64.42%、65.12%、65.46%。随着缺陷的增大，两种情况的稳定承载力下降速率均有所减缓。

4 结论

采用改进塑性铰模型建立了基于刚体准则的空间弹塑性梁单元，运用UL格式的广义位移控制法，以22万m LNG储罐钢穹顶为例，分析了钢网架穹顶结构的屈曲和后屈曲性能，主要结论如下：

1）分析结果与ABAQUS结果的一致性表明，所建立的基于刚体准则的弹塑性空间梁单元模型及其非线性分析方法适用于大型复杂钢网架结构的屈曲和后屈曲分析，具有划分单元及自由度少、可以考虑薄壁型钢截面翘曲影响、刚度矩阵简明、计算效率和精度高的多重优势。与弹性屈曲分析结果的差异表明，材料屈服对网架结构的稳定性具有显著影响，屈曲分析时应予以考虑。

2）网架结构稳定性对初始缺陷较为敏感，荷载干扰和几何缺陷均导致整体稳定承载力下降60%左右。在荷载干扰形成的局部缺陷下，结构初始变形较小，荷载位移曲线在极值点附近突变，主要影响结构极限承载力且局部缺陷的施加位置不同对结果几乎没有影响;在整体几何缺陷下，结构初始变形相对较大，荷载位移曲线较为平滑，主要影响结构失稳形态。

3）常规屈曲分析主要采用模态干扰，需先求解结构初始模态，再乘以系数作为结构整体初始位移缺陷，计算量大，不能反映结构局部缺陷的影响。本文刚体准则单元基于单元的平衡性质而建立，通过施加局部干擾力模拟结构局部缺陷，不必先进行模态分析，计算效率高。

4）网架结构对支座约束条件同样较为敏感。固定支座下，结构稳定承载力高，支座约束的选取对网架结构稳定性影响较大。

参考文献：

[1] 王恒. 大型LNG储罐混凝土外罐及穹顶施工期间全过程受力分析[D]. 哈尔滨： 哈尔滨工业大学， 2014.

WANG H. Complete process analysis of concrete outer tank and dome during the construction period of LNG tank [D]. Harbin： Harbin Institute of Technology， 2014. （in Chinese）

[2] 李斌， 王文焘， 李明. 大型储罐钢穹顶稳定性分析研究[J]. 石油化工安全环保技术， 2019， 35（4）： 31-32，70.

LI B， WANG W T， LI M. Stability analysis of large storage tank steel dome [J]. Petrochemical Safety and Environmental Protection Technology， 2019， 35（4）： 31-32，70. （in Chinese）

[3] BATHE K J， BOLOURCHI S. Large displacement analysis of three-dimensional beam structures [J]. International Journal for Numerical Methods in Engineering， 1979， 14（7）： 961-986.

[4] YANG Y B， CHIOU H T. Rigid body motion test for nonlinear analysis with beam elements [J]. Journal of Engineering Mechanics， 1987， 113（9）： 1404-1419.

[5] YANG Y B， KUO S R. Theory & analysis of nonlinear framed structures [M]. Singapore： Prentice Hall， 1994.

[6] YANG Y B， LIN S P， CHEN C S. Rigid body concept for geometric nonlinear analysis of 3D frames， plates and shells based on the updated Lagrangian formulation [J]. Computer Methods in Applied Mechanics and Engineering， 2007， 196（7）： 1178-1192.

[7] YANG Y B， CHANG J T， YAU J D. A simple nonlinear triangular plate element and strategies of computation for nonlinear analysis [J]. Computer Methods in Applied Mechanics and Engineering， 1999， 178（3/4）： 307-321.

[8] YANG Y B， LEU L J. Force recovery procedures in nonlinear analysis [J]. Computers & Structures， 1991， 41（6）： 1255-1261.

[9] 陈朝晖， 杨帅， 杨永斌. 弹性膜结构几何非线性分析的刚体准则法[J]. 工程力学， 2020， 37（6）： 246-256.

CHEN Z H， YANG S， YANG Y B. The rigid body rule for the nonlinear analysis of membrane structures [J]. Engineering Mechanics， 2020， 37（6）： 246-256. （in Chinese）

[10] YANG Y B， CHEN Z H， TAO Y C， et al. Elasto-plastic analysis of steel framed structures based on rigid body rule and plastic-hinge concept [J]. International Journal of Structural Stability and Dynamics， 2019， 19（9）： 1950104.

[11] 陈朝晖， 陶宇宸， 杨永斌. 基于刚体准则的空间框架弹塑性非线性分析方法[J].建筑结构学报， 2020， 41（10）： 139-149.

CHEN Z H， TAO Y C， YANG Y B. Elastoplastic nonlinear analysis method for spatial frame based on rigid body rule [J]. Journal of Building Structures， 2020， 41（10）： 139-149. （in Chinese）

[12] LIEW J Y R， WHITE D W， CHEN W F. Second-order refined plastic-hinge analysis for frame design. part I [J]. Journal of Structural Engineering， 1993， 119（11）： 3196-3216.

[13] DUAN L， CHEN W F. Design interaction equation for steel beam-columns [J]. Journal of Structural Engineering， 1989， 115（5）： 1225-1243.

[14] 李云飞， 陈朝晖， 杨永斌， 等. 基于刚体准则和广义位移控制法的拱结构屈曲与后屈曲分析[J]. 土木工程学报， 2017， 50（12）： 37-45.

LI Y F， CHEN Z H， YANG Y B， et al. Buckling & post-buckling analysis of arches based on rigid body rule and GDC method [J]. China Civil Engineering Journal， 2017， 50（12）： 37-45. （in Chinese）

[15] BATOZ J L， DHATT G. Incremental displacement algorithms for nonlinear problems [J]. International Journal for Numerical Methods in Engineering， 1979， 14（8）： 1262-1267.

[16] YANG Y B， SHIEH M S. Solution method for nonlinear problems with multiple critical points [J]. AIAA Journal，1990， 28（12）： 2110-2116.

[17] 李忠学. 初始几何缺陷对网壳结构静、动力稳定性承载力的影响[J]. 土木工程学报， 2002， 35（1）： 11-14， 24.

LI Z X. Effects of initial geometrical imperfections on dynamic stability of reticulated shell structures [J]. China Civil Engineering Journal， 2002， 35（1）： 11-14， 24. （in Chinese）

[18] TORKAMANI M A M， SONMEZ M. Inelastic large deflection modeling of beam-columns [J]. Journal of Structural Engineering， 2001， 127（8）： 876-887.

[19] MORRIS N F. Effect of imperfections on lattice shells [J]. Journal of Structural Engineering， 1991， 117（6）： 1796-1814.

（編辑 黄廷）