基于Creo中央空调管道保温棉自动设计和装配研究

郅永亮， 徐梅， 庄志凡

（特灵科技亚太研发中心，江苏 太仓 215400）

0 引言

在进行中央空调制冷管道设计时，为了防止冷气或者热量沿管道壁泄漏导致性能下降，通常需在其外表面安装保温棉。由于这类管道保温棉通常是非标件，研发人员需要根据其具体直管及弯头形状依次进行保温棉组件结构设计。同时，在完成设计时需一并生成原材料零件进行下料，设计示例如图1所示。

图1 保温棉设计示例图

由此可见，基于管道创建保温棉零件和组装的流程比较繁琐，可探索一种自动设计及装配技术来提升效率。而在实际运用中，管道特征参数提取是实现设计自动化的关键要素。在目前已知的一些提取方法中：人为进行几何特征测量直观可控，但效率较低；利用CAD软件的API函数进行检索高效且准确，然而由于管道建模方法多样，必须通过不断迭代算法来实现通用性，且检索易造成算力的浪费。另外，由于管道的结构多变，进行自动配合时各保温棉零件基于整体的默认方向难以判定，影响装配约束的准确性。

因此本文提出一种自动设计及装配的方法，依托Creo设计平台，旨在解决此类零件相关参数获取及装配算法设计的技术难点。原理如图2所示，以参数化三维模型作为模板，同时提取管道参数并建立统一的解析几何数学模型来提取其他设计参数，再借助编程与相关自动宏技术通过一定规则的配合算法及参数的驱动在装配体中完成零件设计与装配，兼顾了产品设计过程中的标准化及参数化。

图2 空调管道保温棉自动装配设计原理

图2中，曲率半径仅为便于下文数学模型中的描述，此处即管道折弯半径。

1 参数化模板设计

对保温棉零件进行统一模板设计是实现自动装配的基础之一。其设计的要点通常包括科学的基准面设定、简易的特征树搭建、材料及渲染属性的正确配置等；其次，为了便于自动化设计时参数调用和后期变更管理，还需定义与管道参数关联的驱动尺寸及一些原材料相关的从动尺寸，如表1所示，并建立一定的参数关系式来确保设计的合理性[1]。

表1 模板参数驱动尺寸表

2 管道设计参数提取

在建立保温棉及其装配所需的管道参数中，除了外径、曲率半径便于提取以外，其余信息则可通过测量各个笛卡尔坐标路径并建立解析几何模型进行转换获取。下文以一段外径为D、曲率半径为R 及路径坐标集

2.1 弯头角度提取数学模型

相邻两直管段之间的弯头角度可通过空间内两向量之间的夹角得出，如图3所示，向量的方向沿管道路径方向，已知各向量的顶点坐标，两相邻向量之间的夹角可通过3个点的坐标的余弦定理得出。

图3 管道弯头角度向量示意图

式中，Xin指第n个空间点的i维度值，如X21指第1个空间点的2维度的值。

2.2 直管长度提取数学模型

如图4所示，相邻的路径点坐标之间的直线长度LAB可由距离公式求出，然而直管长度部分还需由LAB移除相邻所有弯头段直角边得出，弯头段的直角边长度由曲率半径R与1/2弯头角度α正切值的乘积得出。其中，首段直管段n=1与末段直管段n=nmax只需移除相邻一端的弯头部分，而中间的直管段需移除两端的弯头。因此，由这个原理可得第n段直管长度提取模型：

图4 直管长度计算原理图

2.3 弯头空间转角提取数学模型

相邻弯头的空间旋转夹角是装配体组装时唯一一类待求的参数，一般通过两弯头所在的三维空间平面法向量夹角得出[2]，如图5所示。而弯头角度旋转方向则由它所在平面的任一点坐标向量与法向量内积正负来决定，即相当于判定平面方程常量D是否大于0。对本例管道来说，可求解BCD弯头平面法向量相对于ABC弯头法向量夹角及方向，主要公式如下：

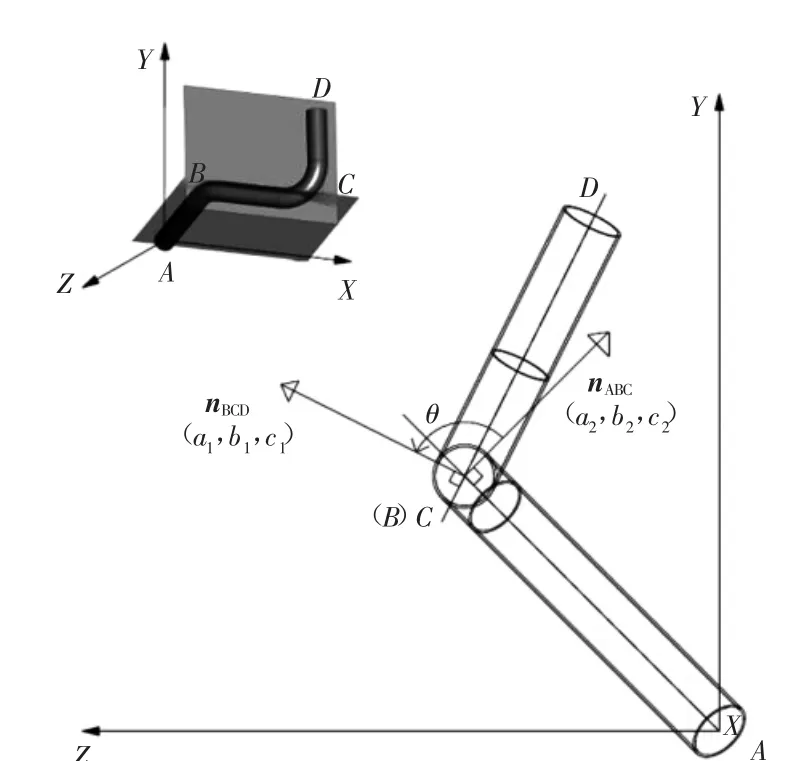
图5 管道空间平面示意图

式中：（a1，b1，c1）、（a2，b2，c2）为ABC和BCD平面的法向量坐标X、Y、Z方向值；D2为BCD平面方程的常量。

因此，可得第n个弯头相对n-1个弯头的空间转角一般式：

其中，第n个弯头平面法向量（a（n），b（n），c（n））及平面方程常量D（n）的一般式如下：

3 自动装配的算法

自动装配的算法研究的主要内容包括保自动装配的配合算法和装配体的参数自动化算法，目的是为了实现保温棉设计及装配流程的自动化。下文主要从这两个角度并结合Creo平台来阐述具体的思路和方法。

3.1 自动装配的配合算法

装配工序条件循环算法。在设计工序算法时通常考虑采用自上而下的原理进行装配，即先创建一个空白装配体，再依次新建基于模板的直管和弯头的保温棉零件并进行约束的整个过程。同时，为了精准控制工序的动态流程，需要引入变量Q 及 循 环 条 件Q ≤Qmax，其中Qmax为总折弯数。当Q≤Qmax时，判定还未完成管道所有部分保温棉的组装，则继续执行下一段的组装，并同时进行Q的累加和判定直到条件识别结果为否，来结束整个装配体搭建，如图6所示。

图6 装配工序算法流程图

预设模式下基于特征ID的保温棉零件约束。在进行每个零件约束之前，将它的默认坐标系与已装配零件的坐标系进行临时的重合来实现方向及位置的预设，该方法能够辅助判定零件的相对方向，为后续约束的进一步定义创造已知条件，降低了装配算法的难度[3]。对于不同零件类型的配合，其参考零件坐标系及约束有所差异。除此之外，定义约束时还需要获取两零件配合的点、线、面元素，在Creo中将这些几何元素转化为特征ID，以便于计算机系统进行识别和分类[4]。

原材料零件自生成。在配合的过程中需要同时添加原材料零件，由于它与设计零件存在一定的关联关系，且相关特征又储存在设计模板中，因此在完成设计模型时可利用自动宏通过激活原材料零件特征创建族表子零件，来快速地完成原材料的自生成。

3.2 装配体的参数自动化算法

1）参数提取自动化。在进行自动装配时，需创建一定的计算机自动化算法规则，快速提取管道全面的参数，以便运用到保温棉CAD模型中。主要原理是依次通过调用区间［1，nmax］路径序号n坐标的方式来批量获取每一位置的直管、弯头、组装的参数信息，而在对每一类参数进行分析运算提取时，又将章节2中的3种提参数学模型分别作为独立模块运行，来提升算法调试及维护的便捷性。

2）参数驱动自动化。将管道参数依次用Creo自动宏同步至装配体及加载完毕的零件来完成设计的最终环节。其中配合参数（空间转角）会同步至装配体驱动具体的约束条件，而零件设计尺寸（如直管长度，弯头角度等）则直接驱动模型中的参数表，这种方法在提高自动化效率的同时还保证了宏的模块化和参数化创建。

具体的参数自动化算法流程示例如图7所示。

4 自动装配程序设计

结合上述自动装配的配合算法及装配体参数自动化的算法，能够设计一套综合的自动装配程序，其内容包括：用户端应用程序的创建来方便用户输入（便于参数录入）；参数处理并返回相关值到用户端（参数表可视化）；调用自动宏作为执行单元自动生成装配（按钮控件）。自动装配用户界面示例如图8所示。

图8 自动装配用户界面示例图

5 结语

通过上述的这种自动装配的理论能够简化参数特征的识别与测量，同时利用计算机实现复杂的运算及建模流程，对于管道类的装配具有一定的借鉴意义。需要注意的是，路径笛卡尔坐标主要是基于常规管道特征进行测量提取，而对于一些变径管道及变曲率管道尚未有深入的研究。