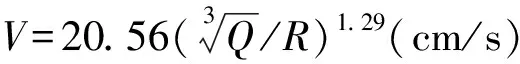不同真空度下地表爆炸后地面振动规律研究

纪晓琳，王小红，李晓杰，闫鸿浩

(大连理工大学 运载工程与力学学部工程力学系，大连 116024)

随着工业工程的快速发展，工业爆破在工程领域的应用越来越广泛。爆破技术在为工程施工带来便利的同时也存在一些安全问题。爆炸会引起土体或基岩的振动，同时产生的冲击波、有害气体、飞石等可能会对爆炸区域周围环境和邻近的地表建筑物造成污染和损害。为避免和减少爆破振动危害，预测和控制爆破振动强度，研究地表爆炸后地面振动规律是十分必要和有意义的。针对爆炸焊接作业，厂房内部的爆炸容器已经成为科研实验利器，不仅降低了往返靶场费用同时也加快了实验进度；如果，加大厂房内部的爆炸容器使用TNT当量，其引起的地面振动需要进行研究，不同药量下的安全距离划定便于后续再建厂房规划参考。

纵观地面振动规律的相关研究，对地铁汽车运行引起的地面振动实测和规律分析的研究较多；邹超等利用某地的实测数据[1]，分析振动加速度在时域频域的变化，得到地铁运行引起的地面振动响应和相关振动衰减规律。爆破引起的地面振动规律的研究的方法已经比较成熟，通常的研究思路是：根据爆炸试验或爆破工程中实测的数据，利用萨道夫斯基公式采用最小二乘法拟合得到相应的振动速度衰减公式。费鸿禄等将利用萨道夫斯基公式反推的质点振速和利用FLAC3D软件数值模拟得到的振速与实际测得的振速进行对比[2]，得出的相关结论以指导方案调整和现场施工。胡建华等基于具体工程试验[3]，结合修正的萨道夫斯基公式采用多元线性化回归法来探究工程岩体的爆破振动衰减规律。冯阳阳等聚焦于爆炸容器内爆炸引起的地表振动[4]，分析了不同炸药量等变量下的振动规律变化。毕卫国等人分析了萨道夫斯基公式的误差来源[5]，并利用编制程序比较各种拟和公式，探讨振速衰减公式的优化选择。

本文开展炸药在真空爆炸容器(用于爆炸焊接科研使用)内，不同真空度下爆炸后地面振动规律研究，通过测点数据研究爆炸后地面振动衰减规律，并进一步分析真空度对爆炸后地面振动效应的影响；同时，预判爆炸容器内不同药量爆炸时的影响距离，以确定爆炸影响范围进行防护。

1 实验方案

1.1 实验测点布置

实验共测试11炮次，2020年9月2日、3日，在爆炸容器(体积250 m3，尺寸不便标注，坐落于硅石矿坑)顶部布置振动速度5#测点，1#、2#、3#、4#测点的具体位置如图1所示，共测试5炮次，实验编号为S1～S5，同期也进行了噪声、壳体动态应变、内壁冲击波超压测量，本文重点分析振动速度规律。9月3日、4日，4#测点的位置调至到爆炸容器门口对面22.5 m处，其他测点位置保持不变，共测试6炮次，实验编号为S6～S11，测点分布见图1。

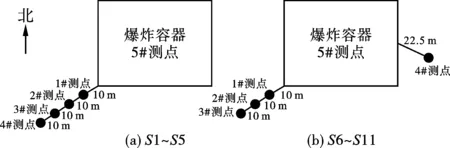
图 1 实验S1～S11监测布点图

在计算分析时，对于S1～S5炮次，由于第二测点数据跳跃3次放弃对该点统计，第5测点放在了真空容器上方的覆盖沙土层测试时速度传感器脱离容器钢板，故放弃对其统计；对于S6～S11炮次，对于第四测点，由于其位于容器开口方向，也做放弃处理。

1.2 测试仪器

地面振动测试采用爆破振动仪及配套的速度传感器来进行数据的采集和记录。在每个测试点布置测振仪器，分析真空爆炸容器爆炸时采集的地震波形，得到各测点的振动速度、频率等重要参数。采集率2 k/s,时间长度设定2 s，调整预触发-400 ms，速度传感器参数为28～30 V/(m/s)。

2 振动测试结果

对于布置在爆炸容器顶部的5#测点处的振动数据并不能反映地基振动与药量的关系，故对测点4、5的数据不做分析。为了清楚地分析真空爆炸容器在不同真空度、炸药量和测点的地基振动影响，根据曲线测试数据，提取了药量、距离、振动合速度、垂直向振动主频等主要参数数据做进一步分析，如表1所示。

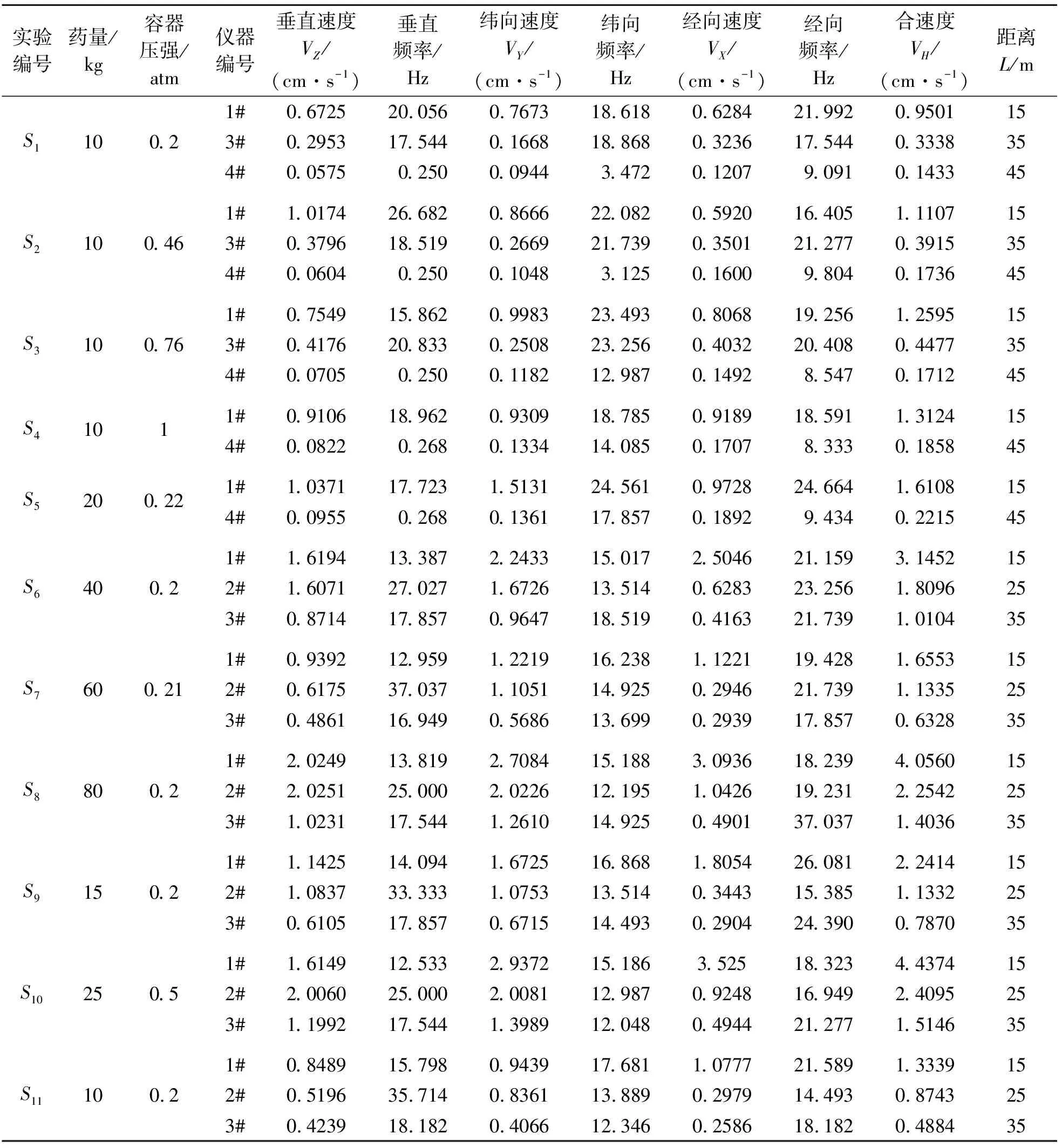
表 1 测点振动检测结果

3 振动结果分析

以表1中实验S11(10 kg、0.2 atm)、S9(15 kg、0.2 atm)、S6(40 kg、0.2 atm)、S8(80 kg、0.2 atm)数据绘制绘制药量和真空度一定时爆炸振速与爆心距的关系曲线，如图2所示。

由图2可知，在药量和真空度一定的情况下，随着爆心距的增加，振动速度逐渐减小。且靠近爆炸源头的区域振动速度随距离的增加衰减迅速。分析相同距离下的振动速度大小可知起爆药量大者其振动速度大，符合实际情况也符合常识，释放能量越大，相同距离下振动速度大，对应结果见图3。

同样以表1中实验S11、S9、S6、S8数据绘制爆心距和真空度一定时爆炸振速与药量的关系曲线，如图3所示，在爆心距和真空度一定的情况下，随着药量的增加，振动速度逐渐增大。且比较3条曲线可知，振速随距离的增加而减小，这与上述结果是一致的。上述结果亦与文献[6,7]的结论保持一致。

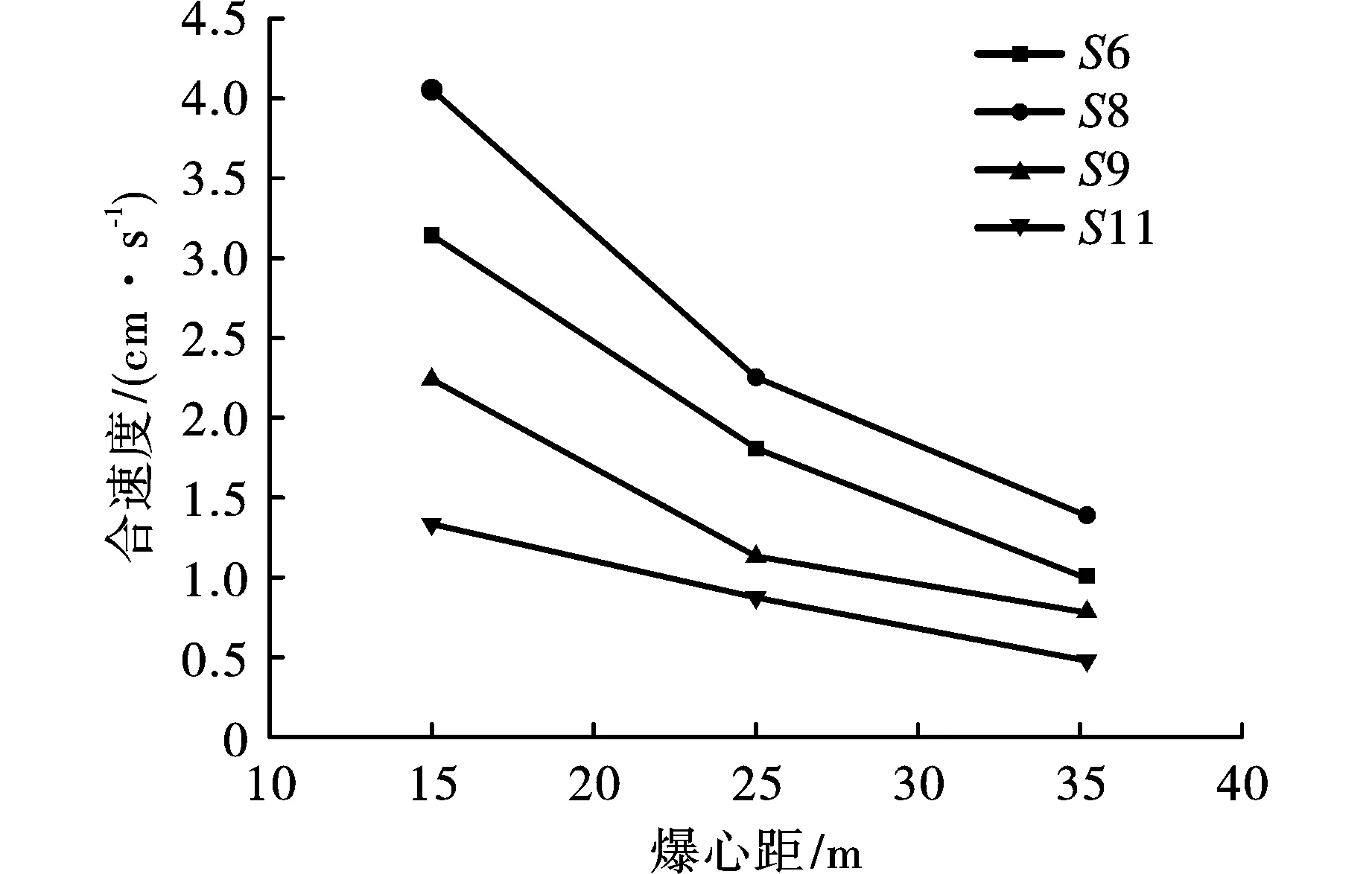
图 2 药量和真空度一定时爆炸振动速度图

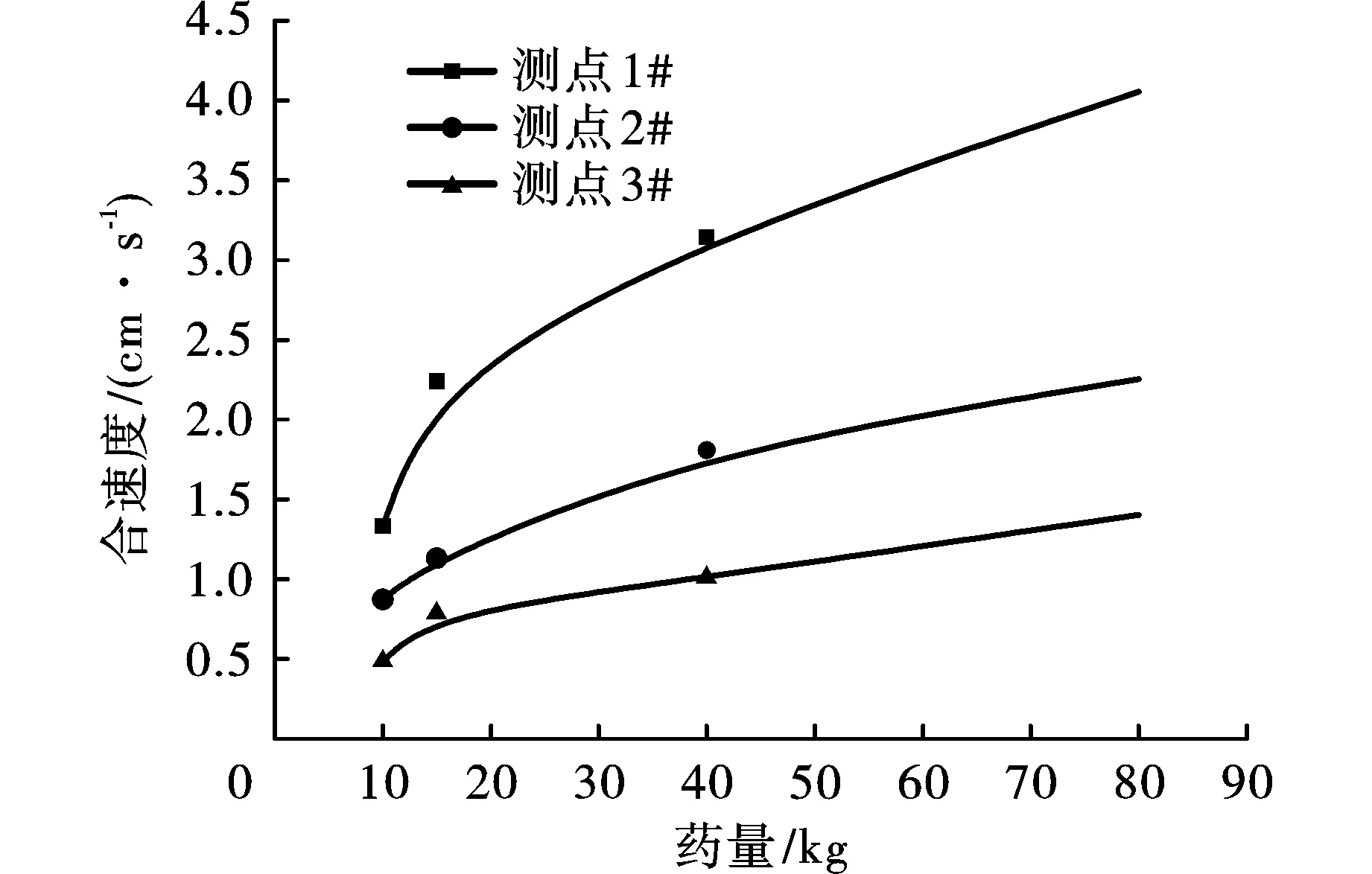
图 3 不同起爆药量下振动速度图

3.1 振动速度回归分析

根据所得数据，现对该测试地点进行振动速度回归分析。采取的方法是：利用萨道夫斯基经验公式，用最小二乘法拟合求取爆破振动参数K、α值，最终得到爆炸振动速度衰减方程。萨道夫斯基经验公式为[8-13]

(1)

式中：V为爆炸引起质点峰值振速，cm/s；Q为药量，kg；R为爆心距，m；K、α为分别为与地质条件和爆炸方式有关的系数和衰减指数。

对公式(1)做如下处理，两边取对数，公式转变为线性方程

(2)

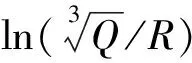
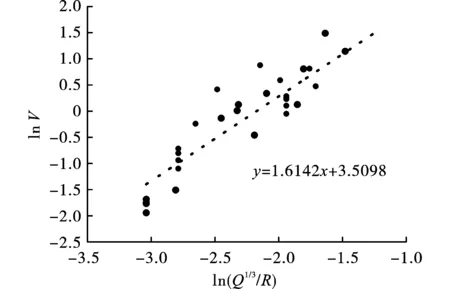
图 4 爆炸振动统计拟合图

3.2 0.2大气压下振动衰减规律

从图4中保留0.2大气压下振动速度数据，用二乘法反演爆炸振动速度衰减规律如图5。

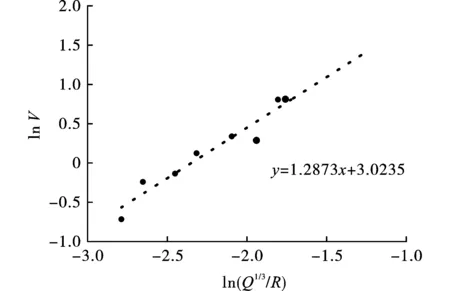
图 5 爆炸振动统计拟合图(0.2 atm)

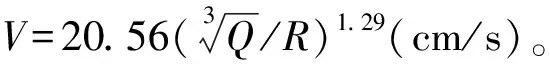
3.3 地面振动衰减规律对照

将3.1节、3.2节反演得到的振动衰减规律综合于图6上。蓝色曲线是综合振动衰减曲线，红色曲线为0.2大气压下的地表振动速度衰减规律；当此距离大于5时，两者相差很微小；在此距离小于5时，真空下爆炸地表振动相对于综合振动数值还是有所减小，这表明当具有真空度时，容器内炸药爆炸引起的近距离振动要小一些，十分符合客观实际。由于炸药在容器内部且布置在底部，炸药与地面直接接触，炸药爆炸产生对地基的冲击会由于真空度变化使得传递给地基的能量降低，但降低量有限。对于远距离预估时，不必要计较真空影响，可以考虑综合情况下振动规律进行计算。

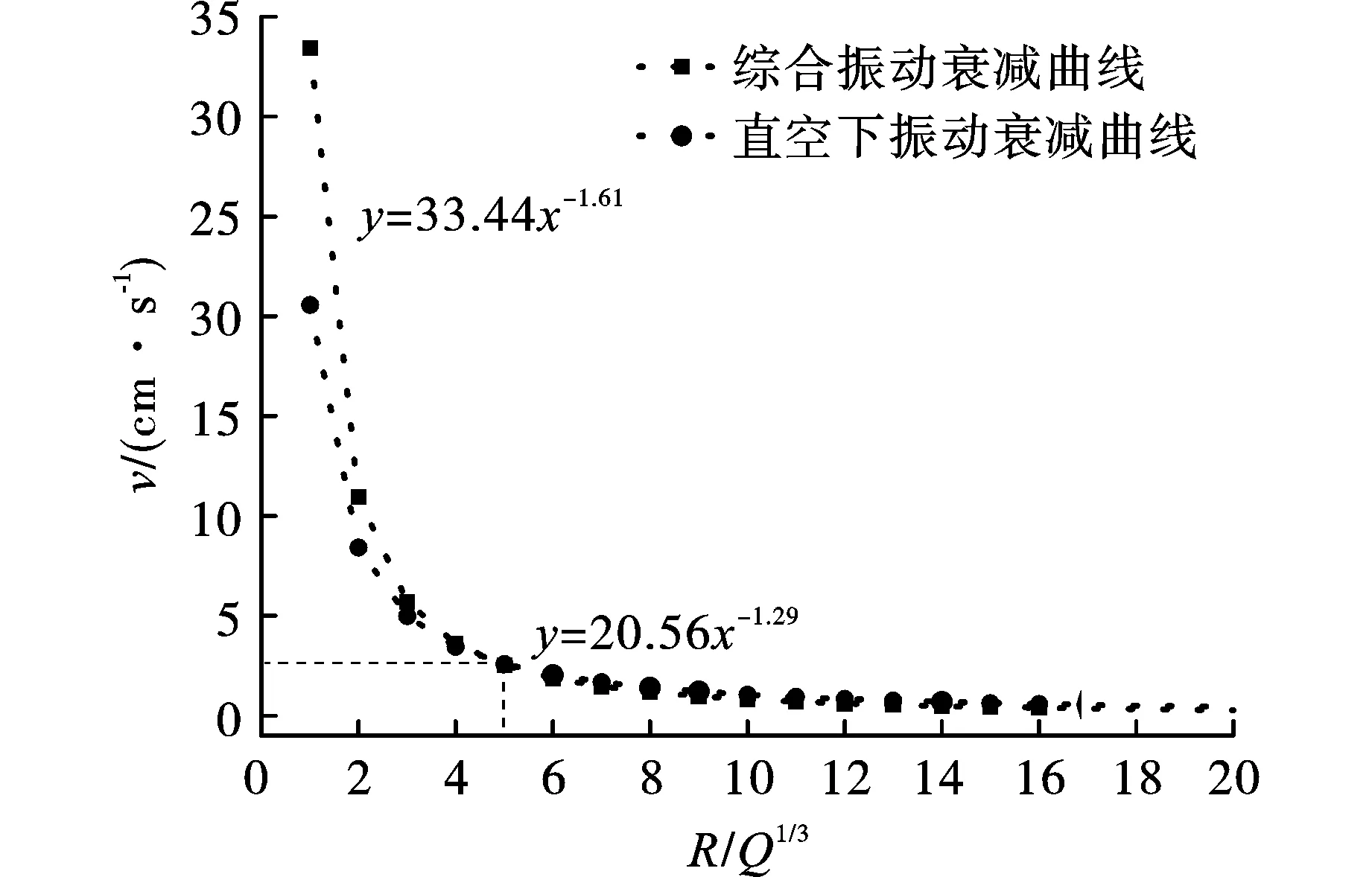
图 6 振动衰减规律对照图

为精细比较真空度影响，将实验S1～S4实验数据单独考虑，统计于图7。对于在15、35 m处测点，真空度0.2～0.46～0.76～1.0变化时，振动速度增加；对于45 m处测点，真空度从0.2向1.0变化时，振动速度变化并不大，这也证明了图6分析的正确性。

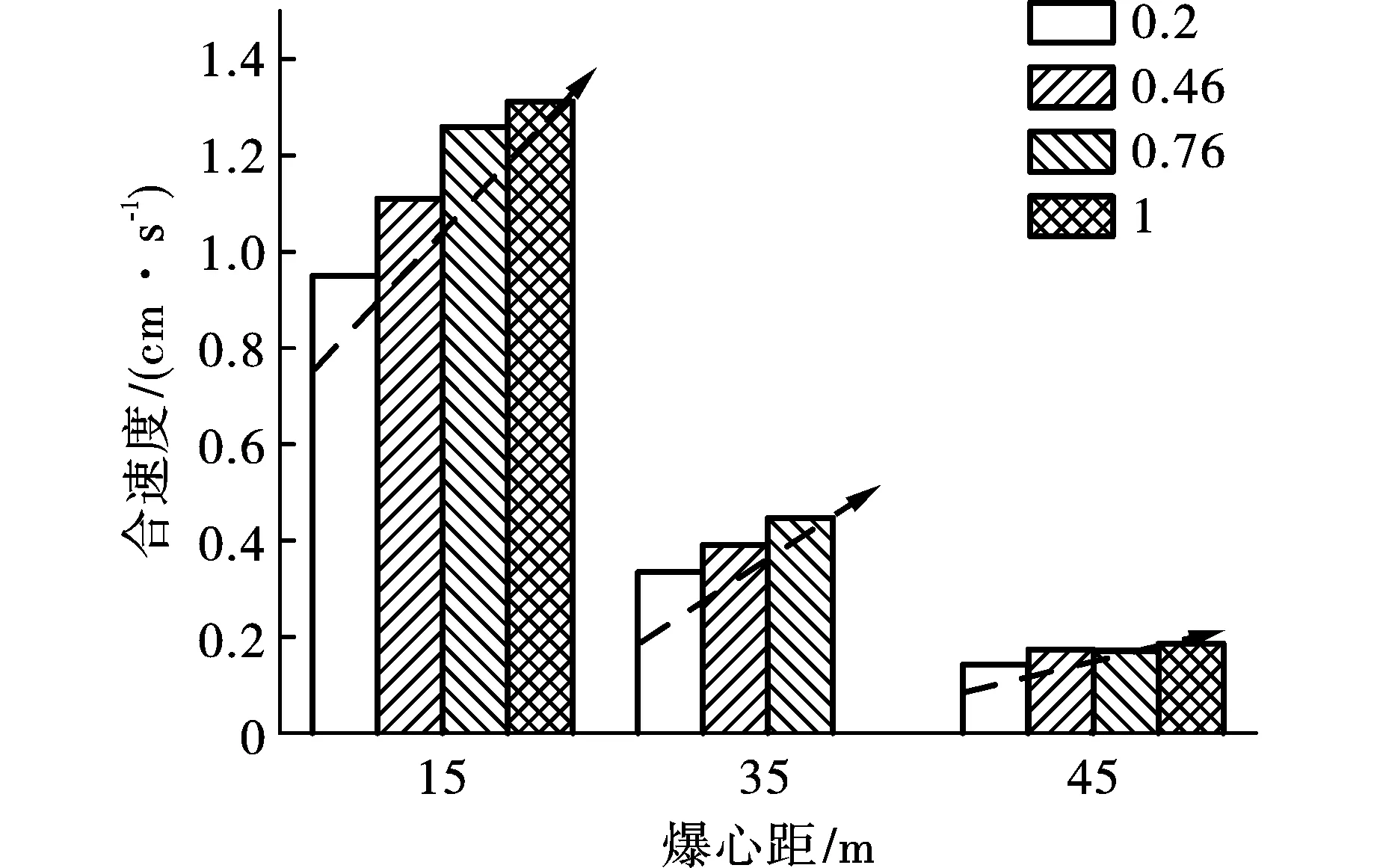
图 7 不同真空度下不同距离处在相同药量下振动速度规律图

考虑真空条件，预判当抽空时即爆炸容器内为负压，远距离处振动影响很小。S1号实验，10 kg炸药，0.20 atm，4#测点，距离45 m，其振动合速度0.1433 cm/s；S2号实验，10 kg炸药，0.46 atm，4#测点，距离45 m，其振动合速度0.1736 cm/s；S3号实验，10 kg炸药，0.76 atm，4#测点，距离45 m，其振动合速度0.1712 cm/s；S4号实验，10 kg炸药，1.0 atm，4#测点，距离45 m，其振动合速度0.1858 cm/s。振动合速度从0.1433变化到0.1858 cm/s，增加很是微弱。根据图7和上述分析，在药量和爆心距相同的情况下，随着容器压强即真空度的增大，合速度缓慢增大，且对远距离处的振动影响很小。

4 预判振动影响距离

爆炸容器是爆炸焊接的主要加工场所，而爆炸焊接场地建设在居民区不太现实，有可能在野外构筑。在野外，可以只考虑“土窑洞、土坯房、毛石房屋”类别房屋。根据《爆破安全规程》(GB 6722—2014)中对此类房屋的爆破振动安全允许标准，在三个频域的振动允许速度为0.15～1.5 cm/s；建议取最小值0.15 cm/s设置防护。爆炸真空容器使用药量从300～700 kg变化，振动速度设置防护标准为0.15 cm/s，其综合压强、0.2 atm下振动影响范围如表2所示。

表 2 安全距离

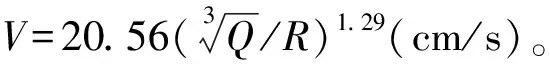
5 结论

以爆炸容器爆炸试验为背景，研究了不同真空度下爆炸后地面振动规律，得到以下结论：

(1)在药量和真空度一定的情况下，随着爆心距的增加，振动速度逐渐减小。且靠近爆炸源头的区域振动速度随距离的增加衰减迅速。在爆心距和真空度一定的情况下，随着药量的增加，振动速度逐渐增大。

(2)当抽空时，即容器为负压，其振动影响很小，由于地基振动的源头来自于炸药爆炸对地面的冲击造成的，在大于5倍比距离时的地基振动在相同距离下变化不大。在药量和爆心距相同的情况下，随着容器压强即真空度的增大，合速度缓慢增大，且对远距离处的振动影响很小。