冰场设计与运动员蹬冰反力数据之间关系的有限元分析与验证

曾雨培，曹金凤，李 策，王志文

(1.青岛理工大学理学院，山东 青岛 266520；2.青岛理工大学机械与汽车工程学院，山东 青岛 266520)

0 引言

影响短道速滑运动员成绩的因素十分复杂，而蹬冰反力是运动员前进的动力来源，因此，本文在不同冰场模型下模拟蹬冰状态，分析不同冰层厚度下不同的蹬冰反力结果。

目前，运动冰场通常采用浇筑防冻抗渗混凝土作为基础，按照人工冰场形式的不同，分为装配式冰场和传统冰场[1]。2种冰场的区别在于装配式冰场的冰层下方是挤塑板，挤塑板的下方是混凝土层，而传统冰场的冰层下方直接铺设混凝土层。

目前，业界借助计算机仿真技术分析不同冰场冰层的厚度对运动员蹬冰反力的影响鲜少涉及。鉴于此，本文基于Abaqus/CAE仿真软件，建立装配式冰场和传统冰场2种有限元模型，讨论冰层厚度对短道速滑运动员蹬冰反力的影响，通过分析不同蹬冰反力结果对冰场设计提供一些指导。

1 国内外研究进展

近年来，国内外的专家学者对人工冰场外部条件及制冷方法进行了分析，旨在降低冰场的能源消耗，提升冰场的能源利用率，从节约冰场能源的角度对冰场建设提出一系列措施。Stubert等[2]提出运用合理建造冰场建筑的方法来降低能源需求，从而改善冰场的可持续性特征。王派等[3]分析了直冷式和间冷式制冷的优缺点，介绍了CO2跨(亚)临界直接蒸发式人工冰场的关键技术和主要性能，体现了很好的节能效果。冰层厚度与制冷系统的运行能耗紧密相关，刘维等[4]对比了国外在室内温湿度、新风量设计标准的异同，给出了针对冰场建筑在空调除湿系统和通风等方面的参考，并结合我国气候特点，提出了合理的冰场温度、冰层设计厚度等设计参数。

在“科技冬奥”的影响下，仿真冰场的分析模拟得到大力推广，刘秀平等[5]针对仿真冰场制定了相应的国家标准，为仿真冰场建设提供更严谨的技术和监管依据。

2 短道速滑蹬冰反力测算方法

本文基于ABAQUS软件[6]建立了冰刀、冰层及混凝土层的三维冰场有限元模型，分析过程中，考虑冰刀从直立状态沿冰刀前进方向沿顺时针逐渐倾斜的过程，每次倾斜5°直至冰刀倾斜至25°。冰层厚度分别为29.1 mm、35 mm、40 mm，装配式冰场中挤塑板厚度为30 mm，传统冰场中混凝土层厚度为100 mm[1]。其他模型参数为:冰刀的长度、宽度和厚度的尺寸分别为430 mm、 24 mm和1.2 mm，倒圆角半径为24 mm；冰面模型的长度、宽度分别为1 000 mm和50 mm。将冰刀、冰层以及混凝土层的三维模型进行装配，形成完整的传统冰场有限元模型。建模过程中，冰刀前进方向为x轴，与x轴垂直且沿着刀身向外方向为y轴，垂直冰刀刀身方向为z轴。

冰刀、冰及混凝土的材料参数设置为[7]:冰刀材料为钢，弹性模量为210 Gpa，泊松比为0.3；冰的密度为920 kg/m-3[8]，弹性模量为8.58 Gpa，泊松比为0.33[9]；挤塑板的密度为30 kg/m-3，弹性模量为6.6 Mpa，泊松比为0.28；混凝土密度为2 500 kg/m-3，弹性模量为30 Gpa，泊松比为0.2。冰刀与冰层之间的摩擦设为滑动摩擦，摩擦系数为0.005[10]；冰层与挤塑板间采用摩擦罚接触，摩擦系数设置为0.1；冰层与混凝土层之间的摩擦设为切向罚接触，摩擦系数为0.1。对混凝土层底面四周施加固定约束，在冰刀上表面设置耦合作用点，在作用点上施加运动员的运动参数，运动员在滑行中，施加自重荷载外，加速度为12 m/s2，速度为11.28 m/s(女性运动员的平均速度)，定义的有限元模型如图1、图2所示。

图1 装配式冰场有限元模型

图2 传统冰场有限元模型

ABAUQS/Explicit显式求解器[11]适合模拟短暂、瞬时的冰刀蹬冰动作，蹬冰过程中冰刀与冰层表面接触时间较短，根据国家体育总局训练中心所做测试数据，设置冰刀与冰面接触时间为0.003 5 s。

3 试验结果分析

选取冰层厚度分别为29.1 mm、35 mm、40 mm以及蹬冰角度逐渐倾斜至25°的工况，基于Abaqus软件对运动员在装配式冰场模型与传统冰场模型进行研究，获取各个工况的竖向反力与侧向反力。

侧向力与运动员前进的驱动力更为相关，选取倾斜5°、15°、25°时装配式冰场和传统冰场的分析结果，如图3～8所示。

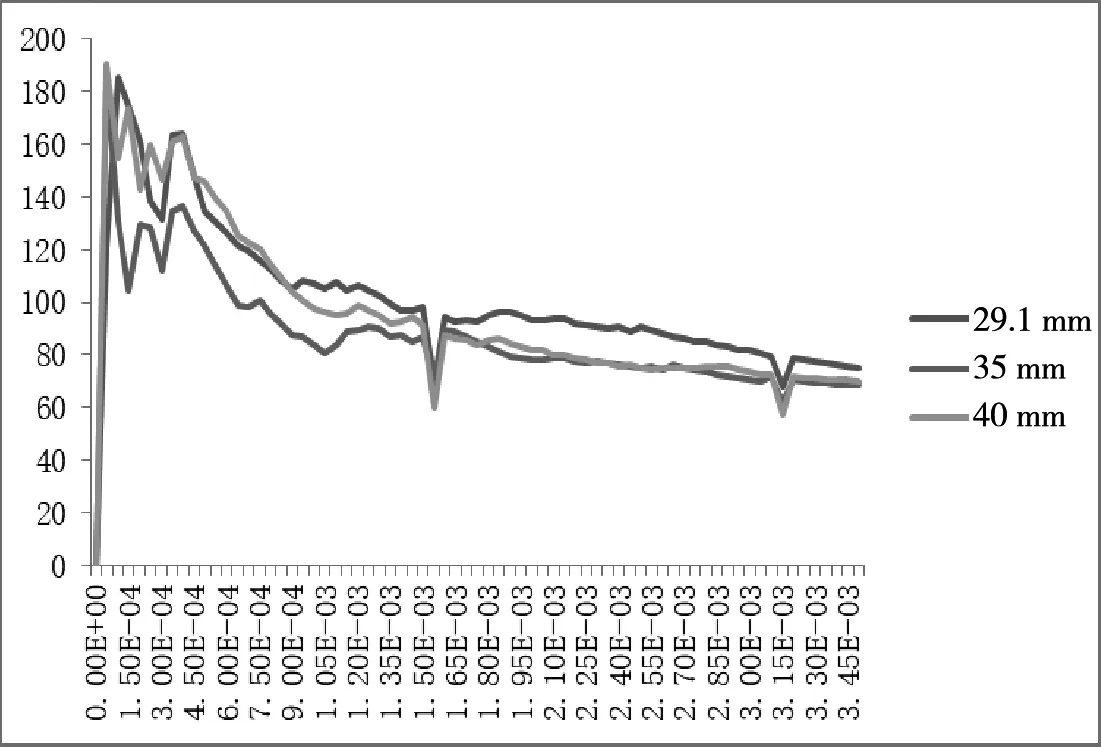
图3 装配式冰场冰刀倾斜5°滑行侧向反力

图4 传统冰场冰刀倾斜5°滑行侧向反力

由图3和图4可知，当蹬冰角度为5°时，29.1 mm厚冰层对应的侧向反力均值最大，35 mm和40 mm厚冰层的侧向反力均值曲线基本重合。

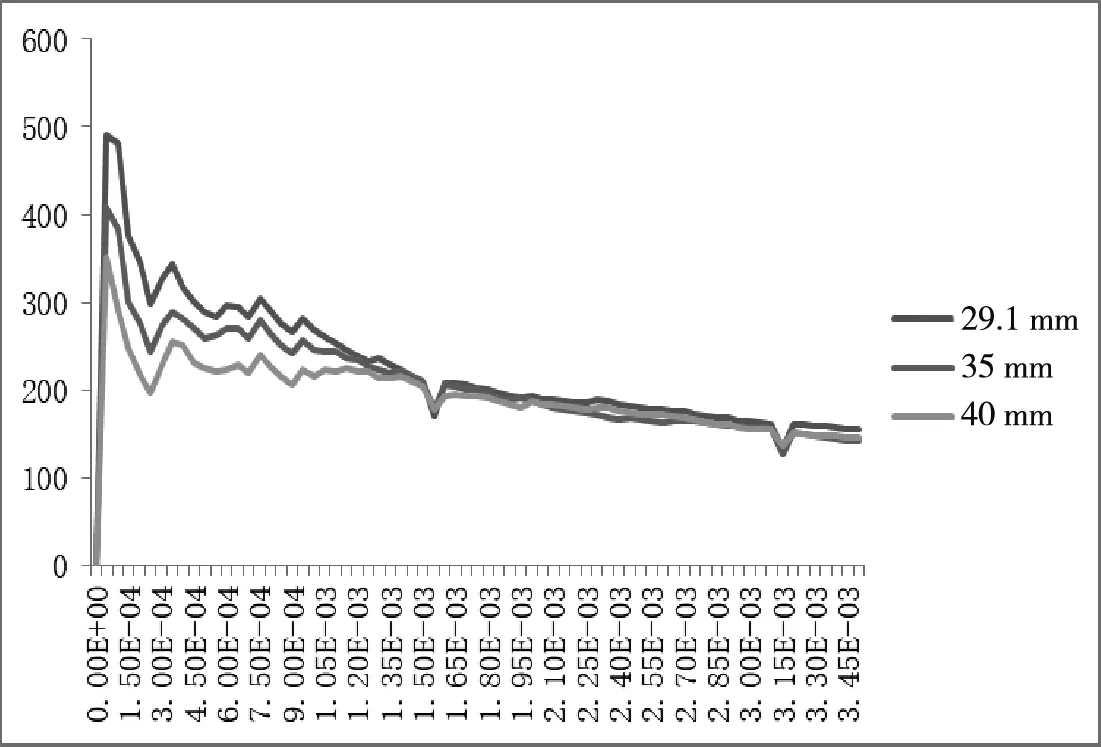
图5 装配式冰场冰刀倾斜15°滑行侧向反力

图6 装配式冰场冰刀倾斜25°滑行侧向反力

由图5、图6可知，不同冰层厚度的装配式冰场模拟的侧向反力均值曲线随着冰刀倾斜角度的增加，曲线逐渐重合，且冰层越厚，初始时间附近的侧向反力均值越小；当冰刀倾斜25°时；40 mm、35 mm和29.1 mm厚冰层对应的侧向反力均值分别为237.59 N、229.85 N、229.13 N，后两者的侧向反力均值接近，意味着当冰层厚度超过35 mm时，即使厚度值增加，侧向力值增加也偏小。

图7 传统冰场冰刀倾斜15°滑行侧向反力

图8 传统冰场冰刀倾斜15°滑行侧向反力

由图7、图8可知，对于传统冰场模型，在冰刀倾斜15°时，分析步时间的前半段，冰层厚度35 mm时，侧向反力均值最大，分析步时间的后半段，冰层厚度越大侧向反力均值增加逐渐加快；随着冰刀倾斜角度的增加，当冰刀倾斜至25°时，分析步时间前半段，冰层越厚侧向反力均值越小，随着分析步时间的增加，由图8可知，3条曲线逐渐重合，侧向反力均值变化的规律与分析前半段的规律相同。

4 结论

短道速滑冰场的设计、建设工作，不仅与运动员速滑成绩密切相关，更与能源消耗相关。本文针对装配式冰场、传统冰场建立有限元模型，分析不同冰层厚度、不同蹬冰角度等工况，得出以下结论。

1)短道速滑装配式冰场在直道滑行区冰层应较薄，弯道加速区冰层厚度对侧向反力均值影响较小，从经济角度考虑，弯道加速区冰层厚度不宜过厚。

2)短道速滑传统冰场弯道加速区域冰层应略厚于直道滑行区，以提供较大侧向驱动力。

3)当冰层厚度超过35 mm时，增加冰层厚度对驱动力的增加影响较小，建议冰层厚度取35 mm左右较合适。