基于虚拟电感的PMSM无位置传感器混合控制策略

骆 攀，刘 鎏，青先国，谢 峰，赵俊杰，陈凯旋

(中国核动力研究设计院核反应堆系统设计技术重点实验室，成都 610041)

0 引 言

表贴式永磁同步电机(SPMSM)因功率密度高、运行可靠、力能指标和控制特性好等优点，被广泛应用于数控机床、机器人、新能源汽车、航空航天等各种驱动领域。为实现高性能PMSM驱动调速控制，多采用较精密的机械式编码器来获取转子的位置或速度信息。然而，所采用的机械式编码器不仅会增加系统体积和成本，其往往也是整个驱动控制系统中的脆弱环节，易受震动，灰尘，湿度等运行工况的影响。一旦编码器发生故障，容易导致系统发生飞车，损坏设备甚至造成人员伤亡等事故。此外，机械式编码器的安装维护困难、连接线路复杂、易受噪声和电磁干扰等缺陷也会降低电机驱动系统的整体可靠性。因此，研究PMSM无位置传感器控制技术在过去几十年内得到了国内外许多研究学者的关注[1-11]。

根据转速的适用范围不同，无位置传感器控制技术可大致分为低速方案和高速方案。其中低速方案又根据电机控制方式的不同，可进一步分为闭环控制方法和开环控制方法。低速闭环控制方法是通过注入额外高频信号或插入有效的PWM电压矢量去耦合与转子位置信息相关的凸极信息，从而获取转子位置信息，包括基于瞬态电流检测法[1]和高频信号注入法[2]。这类方法原理简单、易于操作且不依赖电机参数，但需要注入额外的高频激励信号，其动态性能和带载能力一般，较适合于那些对带载能力和动态性能要求不高的低速应用场合。低速开环控制方法主要包括电压频率比(V-F)控制[3-4]和电流频率比(I-F)控制[5]，这类方法不需要准确的转子位置信息，仅通过定子绕组产生开环旋转磁场带动转子运行，因此对应用环境具有较强适应性。但V-F控制方法本质上是一个开环控制结构，容易引起转矩波动和过流现象，特别是当电压频率比选取不恰当时易烧毁功率器件。相比于V-F控制方法，I-F控制方法是电流闭环控制结构，其转矩与功率角间的自稳定性使其具备较强的带载能力和动态性能，且所采用的电流调节器还能有效防止电流过冲。但随着转速升高，其转矩与功率角间自稳定性能会逐渐下降，直至不稳定。因此，I-F控制方法较适合于那些对带载能力和动态性能要求较高的低速应用场合。

当电机工作在额定转速10%以上的高转速段时，足够大的反电动势(Back Electromotive Force, BEMF)可以提供强信噪比的转子位置信息。目前，适用于高转速段无位置传感器控制方法主要包括：磁链估计法、卡尔曼滤波法、状态观测器法、模型参考自适应法以及滑模观测器法[6-8]。每种方法都有其各自的优缺点。磁链估计法计算量小，但易受采样噪声影响，因此需要高性能的滤波器。卡尔曼滤波法可以消除白噪声干扰且位置和速度估计精度高，但计算量大，需要增加硬件处理器成本。状态观测器法和模型参考自适应法都易于实现，但对电机参数的依赖性较高。滑模观测器法具有较快的响应速度、对系统内部参数和外部干扰具有较强的鲁棒性，但存在严重的抖振问题。随着学者们对各种方法的深入研究，各种高速反电动势法的性能也得到了相应的改善，在中高转速区域都能获得较好的控制效果。但随着转速的降低，较小的反电动势无法提供转子的有效信息，因此不适用于低速区域，还会出现启动失败的问题。因此，目前还没有一种成熟的方案能高效、稳定地实现全速域永磁同步电机无位置传感器控制。通常的做法是采用高、低速混合控制策略[9-11]，即在电机低速阶段，采用I-F、高频信号注入等低速方案，加速至一定速度后再切换至基于反电动势估计的高速方案，最终实现全速域无位置传感器控制运行。但由于存在高低速两类方法的切换，为了使转子位置和转速在切换的速度区域内不会出现大的波动，就需要设计合适的切换策略。常用的切换策略是加权算法，它可以取得较平稳的切换过程，但在计算过程中需要对转速信息进行迭代运算，从而降低了系统的稳定性。此外，过渡区间的选择也需要根据经验或者测试进行确定。参照加权算法的思路，也有学者结合高频信号注入和反电动势模型，提出了一个基于锁相环的切换思路，通过合理的设计锁相环带宽，可以快速、平稳地实现高低速方案切换，但仍存在加权系数需要根据经验或反复尝试来确定。

综上所述，尽管利用高低速混合控制策略能实现永磁同步电机全速域无位置传感器控制，但其控制性能会受高低速方案切换的影响，严重时甚至会导致系统振荡。因此，本文在低速I-F开环控制和高速反电动势模型法相结合的混合控制策略的基础上，提出了一种基于虚拟电感的高低速平滑切换策略。针对两种方法因建立在不同坐标系而存在的控制结构差异问题，提出方案以I-F方案的坐标系为参考模型，反电动势模型为可调模型，运用Popov超稳定理论设计出恰当的虚拟电感使可调模型收敛于参考模型，从而确保两种方案在切换前始终建立在同一坐标系上，以实现高低速平滑、稳定地切换。

仿真和实验验证了所提方案的可行性和有效性。

1 基于虚拟电感的混合控制策略

当忽略电机交叉饱和效应以及多重凸极效应时，在两相静止αβ坐标系下，表贴式永磁同步电机的数学模型可表示为

Vαβ=Rsiαβ+Lsiαβ+λpmej(θr+π/2)

(1)

式中，Vαβ、iαβ、Rs、Ls和λpm分别为定子电压矢量，定子电流矢量、定子电阻、定子电感和永磁体磁链。其中θr为d轴与α轴间的夹角，也即电机的转子位置。

1.1 高速反电动势模型法

当电机运作至中高速范围时，足够大的反电动势能提供可靠转子位置信息。因此，通过对式(1)进行重新排列和运算后，可得到转子位置的表达式为

(2)

式中,Arg和LPF分别表示取矢量的相角和低通滤波器。低通滤波器的使用是为了消除纯积分器的直流偏置问题。然而，低通滤波器的使用不仅会造成输入信号幅值和相位的变化，引起转子位置估计偏差；还限制了在低通滤波器截止频率以上的基波有效控制。因此，为了补偿低通滤波器带来的影响，首先，选取低通滤波器的截止频率同转子转速相关，可用Tωr表示。其中，T是一个固定的常数，取值范围一般在0.3到1.0；T值越大，滤波效果越好，动态响应越快，但引起的偏差也越大；所以T的取值需要进行综合考虑。为了方便分析，对表达式(2)的两边同时进行拉普拉斯变换并以复数形式表示为

(3)

其中,M= 1+Tωr/s，s为拉普拉斯算子。复数M就是由低通滤波器引起的偏差，包括幅值和相位的偏差。当电机运行在稳态状态时，拉普拉斯算子s可等价于jωr。再将s=jωr代入复数M的表达式中，发现复数M等于一个常数(1-jT)。随后，通过直接补偿M，可完全消除了由低通滤波器导致的转子位置估计偏差。 再利用得到的转子位置和速度信息可以构建速度-电流双闭环矢量控制算法，最终实现永磁同步电机高性能无位置传感器控制运行，如图1所示。其中，在高速运行时，1与3相连接，θBlend为磁场定向角。

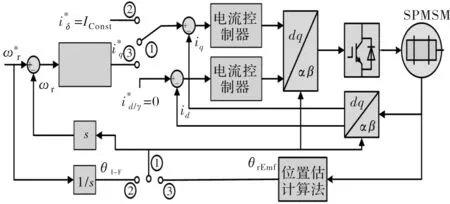
图1 SPMSM无位置传感器闭环控制框图

1.2 低速I-F开环控制

(4)

Te=1.5npλpm(-iγsinφerr+iδcosφerr)

(5)

由于在I-F控制方案中iγ控制为零，因此其输出电磁转矩大小由偏差角φerr决定。为了保证I-F 控制方法的稳定性，偏差角φerr必须控制(-π/2,π/2)内。由于可以控制电流幅值以满足最大额定负载需求，在I-F控制方法正常工作时，偏差角φerr会随着负载大小在稳定区间内自动调节。因此，这种转矩与功率角间的自稳定性使电机在低速运行时具备较强的带载能力和动态性能，且所采用的电流调节器还能有效防止电流过冲。

图2 不同坐标系之间的空间位置关系图

1.3 基于虚拟电感的平滑切换策略

根据上述的描述，PMSM采用I-F开环控制与基于反电动势模型法的速度-电流双闭环矢量控制相混合的，能分别满足电机低速和高速的控制性能。但从速度开环-电流闭环的低速运行状态到双闭环矢量控制的高速状态，中间需要一个过程进行方案切换，如图1所示，低速运行时1与2相连接；当转速加速到一定数值时需切换至1与3相连。又观察图2(a)可知，低速I-F开环控制是建立在γδ坐标系而高速反电动势模型法建立在dq坐标系。这两种方法建立在不同的坐标系，存在着控制结构上的差异，若直接切换必定会引起转速和电流的波动，造成系统振荡。因此，为了使状态切换能够平滑进行，在过渡过程中转速和电流无冲击，需要提出一种平滑、稳定的切换策略。

首先将PMSM的数学模型用相量图的形式来表示，如图2(b)所示。其中us、is、xs分别表示定子电压空间矢量、定子电流空间矢量和定子感抗。由图2(b)可以看出，γδ坐标系与dq估计坐标系存在角度偏差，直接切换必定会引起系统波动。但如果通过设计一个虚拟电感去取代替定子电感Ls使θrEmf直接等于(π/2-θI-F)而不是转子位置θr，即drEmfqrEmf坐标系在高低速方案切换前始终与γδ坐标系对齐，如图2(c)所示。在统一的坐标系上再进行方案切换就能保证切换的平滑性和稳定性。基于此思路，采用模型参考自适应的设计框架，以I-F方案的γδ坐标系为参考模型，反电动势模型为可调模型，运用Popov超稳定理论设计出恰当的虚拟电感使可调模型收敛于参考模型，从而确保两种方案在切换前始终建立在同一坐标系上，也即偏差角φerr为零。因此，将φerr=0代入式(4)中，可得I-F方案控制下的参考模型，用坐标分量的形式可表示为

(6)

式中，Ls1是待定的虚拟电感值，在电机以I-F控制稳定运行时，其为常数。为了获得准确的Ls1，再将式(6)用估计值表示为可调模型，则有

(7)

将式(6)减去式(7)，可得误差状态方程为

(8)

其中,

由式(8)可知，它是一个标准的等效非线性反馈系统，根据Popov超稳定理论，需要满足以下积分不等式

(9)

(10)

再将式(8)和式(10)分别代入式(9)，可得

(11)

(12)

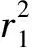
(13)

式中,k大于零。在这里，取

(14)

再对式(14)两边进行求导，则有

F1(v,t,)=KieTB(Ki>0)

(15)

F2(v,t)=KPeTB(kP>0)

(16)

(17)

进一步地，当电机运行在稳定时，电流微分可近似忽略，式(17)可简化为

(18)

图3 基于模型参考自适应的虚拟电感估计

2 实验验证

本节通过实验对所提出的基于虚拟电感的无位置传感器混合控制策略有效性和实用性进行验证。实验测试平台如图4所示。测试的SPMSM规格和参数如表1所示。负载转矩由拖动电机提供。采用分辨率为2500线的增量编码提供实际转子位置以供实验对照。整个控制算法在ADI处理器ADSP-CM408上执行。电流采样频率与PWM开关频率都为10 kHz。所有的实验结果都用D/A模块传送到示波器中显示。

表1 电机参数

首先，按照控制框图1所示，将1与2相连接，采用I-F控制电机稳定运行于切换速度(一般取额定速度的20%)，同时也使用反电动模型法检测转子位置。图4给出了高低两种方案的磁场定向角相对于真实位置的位置偏差。I-F 控制方法为了确定自稳定性，q轴的恒定给定电流通常会在额定值以上，导致γδ坐标系与dq坐标系之间存在一定的角度偏差，即φerr约为50°，如图4(a)所示。而从图4(b)中可以看出反电势模型法在切换速度处可以得到较为准确的位置观测值。由于两种方案所在的坐标系之间存在较大的位置偏差，如果直接进行方案的切换，将导致磁场定向角度产生较大的跳变，影响系统的稳定运行。

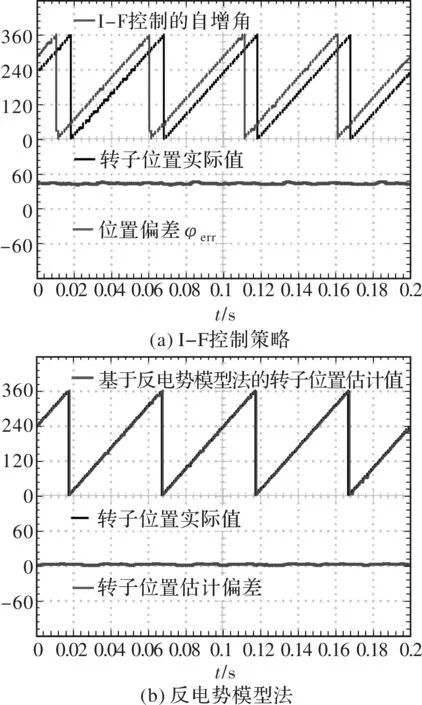
图4 两种位置检测方案的角度对比

为了进一步验证所提基于虚拟电感的无位置传感器混合控制策略的有效性，图5进行从零速到额定速度1500 r/min的实验。在20%额定转速(20 Hz)进行高低速方案切换，对应于图5中的T2时刻。在T2之前，采用I-F控制电机加速运行。随着转速的上升到一定值时，足够大的反电势能提供转子位置信息，因此在T1之后开始进行虚拟电感的自适应辨识。当转速加速至切换速度T2时，由于高低速两种方案的偏差角φerr收敛至零，电机控制方案直接由I-F单电流闭环控制切换至基于反电势模型法的双闭环控制，对应于图1中的1与3相连接。T2之后，为了不影响电机的高效率输出，虚拟电感又逐渐减小于定子电感的实际值。从实验结果可以看出，电机能稳定地从静止加速至额定转速，且在加速过程中转速和电流几乎没有较大的波动，这表明提出的基于虚拟电感混合控制策略能实现快速、稳定的PMSM全速域无位置传感器控制运行。

图5 提出基于虚拟电感混合控制策略从静止加速至满速的动态实验结果

3 结 语

本文提出了一种基于虚拟电感的无位置传感器混合控制策略，以提高PMSM全速段无位置传感器控制性能。针对低速I-F控制方法和高速反电势模型法的切换振荡问题，在电机模型中通过引入虚拟电感来人为改变其转子位置估计值；再以I-F方案的坐标系为参考模型，反电动势模型为可调模型，运用Popov超稳定理论设计出恰当的虚拟电感使可调模型收敛于参考模型，从而确保两种方案在切换前始终建立在同一坐标系上，以实现高低速平滑、稳定地切换。最后，实验结果表明，所提出的混合无传感器控制策略在整个速度范围内具有良好的稳态和动态控制性能。