平动位移下衡重式挡墙背土体破裂面特征及土压力分析
罗 强 熊诗杰 王腾飞 黄 豫 张 良
(1西南交通大学土木工程学院, 成都 610031)(2西南交通大学高速铁路线路工程教育部重点实验室, 成都 610031)
衡重式挡墙是为适应我国西部山区地形出现于20世纪50年代的一种重力式挡墙结构形式,具有圬工量少、收坡效果好、施工方便及造价低廉等优点,使用效果良好[1].衡重台的存在使得衡重式挡墙受力特性发生较大变化,上下墙背间相互影响,土压力计算方法较为复杂.实际工程应用中,衡重式挡墙变形过大甚至失稳,尤其是上墙与衡重台交界处拉裂破坏等现象时有发生,现有的挡墙结构设计方法存在一定的安全风险.
国内外学者对衡重式挡墙受力特性及土压力计算方法进行过诸多研究.衡重式挡墙背土压力的计算以Coulomb理论为基础,采用折线形墙背的土压力计算方法[2].文献[3]根据铁路路基挡墙的各种边界条件,推导出最不利滑动面倾角及第二破裂面上最大水平土压力的计算公式.文献[4]根据上墙和衡重台无摩擦假定,将二裂面土压力转化至上墙背,并推导出采用力多边形法计算下墙土压力的公式.文献[5-7]通过衡重式路肩墙的离心模型试验发现,挡墙不同位移模式对下墙土压力分布有明显影响,挡墙平动时为三角形分布,挡墙转动时为折线形分布;而上墙土压力分布基本不受影响,均为三角形分布.文献[8]通过模型试验和有限元分析,认为上下墙土压力在土体变形过程中相互影响,土体间相对运动产生的卸荷拱使得下墙土压力减小,而上墙受力远大于规范计算值.文献[9]基于对折线形挡墙受力形式的理论分析及缩尺模型试验,认为拱效应使上下墙土压力分配产生较大变化,造成上墙土压力增大而下墙土压力减小.
卸荷板式挡墙在结构和受力形式上与衡重式挡墙类似,尤其是上墙部分.文献[10]通过短卸荷板式路肩挡墙的离心模型试验发现,上墙土压力呈三角形分布,下墙土压力呈两边小中间大的分布,上墙背实际受力大于Coulomb土压力计算值,并建议将规范计算值乘以1.4的放大系数.文献[11-12]分别通过卸荷板式挡墙的模型试验和数值模拟,分析了卸荷板宽度对滑动面特征及墙背土压力的影响,得到了可有效降低土压力的最佳板宽.文献[13-14]进行了衡重式桩板挡墙模型试验,指出卸荷板存在最佳埋深位置,卸荷板埋深和宽度对上墙土压力分布情况无明显影响.
已有的衡重式挡墙研究加深了对具有衡重台或卸荷板等复杂墙背的土压力特性认识,但研究对象多为路肩墙,现有规范设计方法难以准确反映墙体承受的土体作用,导致土压力计算值与实测值之间存在较大偏差.对于使用较少、关注度较低的路堤墙,边坡高度和坡率等因素可能会进一步增大计算方法缺陷造成的误差,存在更大的安全隐患.因此,需要对折线形复杂墙背条件下的土体破裂面特征与土压力计算模式进行研究.
本文利用有限元方法,针对平动位移模式下的衡重式挡墙,研究墙背土体的破坏模式,包括上墙第一、第二破裂面和下墙破裂面的萌生、演化过程以及贯通后的形状和倾角.分析上、下墙背和衡重台土压力的分布规律以及土压力随挡墙位移的变化趋势,并将有限元计算数据与离心模型试验和规范计算结果进行对比,探讨破裂棱体形态、土压力在上墙和下墙间分配等产生差异的主要原因.最后,针对上墙第一破裂面难以形成的现象,引入反映剪切角发挥程度的系数η,建立衡重式挡墙土压力计算修正模式,为完善衡重式挡墙结构设计奠定基础.
1 土压力计算模式
衡重式挡墙土压力计算模式见图1.墙顶与衡重台边缘连线ac为假想墙背,按折线形墙背计算土压力,假想墙背摩擦角即为土体内摩擦角φ.若ac俯斜程度较大,墙背土体破坏时会在上墙产生2个破裂面cd和cg,按照第二破裂面法计算土压力;在下墙产生破裂面om,按照力多边形法计算土压力.图中,E′、E1、E2、P分别为第二破裂面、上墙背、下墙背及衡重台的土压力;W、W′、W″分别为土体abcd、cdeg、cgmo的质量;α′、α1、α2、λ分别为假想墙背、上墙背、下墙背及边坡的倾角;δ2为下墙背摩擦角;β、α、θ分别为上墙第一、第二破裂面及下墙破裂面倾角;R1、R2分别为第一破裂面和下墙破裂面的反力.

图1 衡重式挡墙土压力计算模式
第二破裂面法计算公式基于Coulomb理论推导,由破裂棱体cdeg的静力平衡条件(见图2(a)),第二破裂面水平土压力E′x=f(α,β),对其求偏导可得
(1)
(2)
由式(1)和(2)求得2个破裂面倾角α和β,进而得到E′x、E′及竖向分力E′y.基于上墙背及衡重台均无摩擦的假定,根据衡重台上土体abcd的静力平衡可得作用于实际上墙背的土压力E1(见图2(b)).

(a) 土体cdeg
下墙土压力计算方法包括延长墙背法和力多边形法,工程设计常采用后者.由破裂棱体cgmo的静力平衡条件可知,下墙土压力可表示为E2=f(θ),根据dE2/dθ= 0解得θ,进而得到下墙土压力E2(见图3).

图3 下墙背土体力多边形
2 有限元模拟及数据分析
2.1 计算模型及参数
在ABAQUS软件中采用平面壳单元(2D Planar-Shell)模拟衡重式挡墙路堤断面.衡重式挡墙路堤断面示意图见图4.总墙高H=8 m,上墙高H1=3.2 m,下墙高H2=4.8 m,墙顶宽B1=0.5 m,衡重台宽L=1.98 m,墙底宽B2=2.4 m,路堤边坡高度h=8 m.
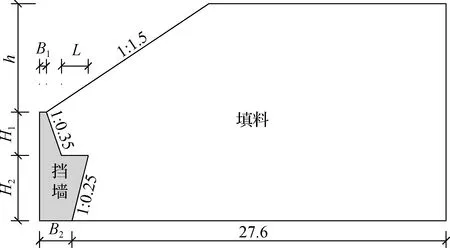
图4 衡重式挡墙路堤断面示意图(单位:m)
2.1.1 材料参数
采用砂土作为墙背填料,视其为理想弹塑性材料.土体屈服准则采用Mohr-Coulomb准则,线弹性阶段的参数包括弹性模量ω和泊松比μ,塑性阶段的主参数包括内摩擦角φ、剪胀角ψ和黏聚力C.计算中,黏聚力C不能为0,对于砂性土取C=1.0 kPa.挡墙采用C25混凝土,按理想线弹性材料处理,材料参数根据《混凝土结构设计规范》(GB 50010—2010)[15]取值(见表1).

表1 材料物理力学参数
2.1.2 接触作用与荷载施加
设置墙-土接触属性,接触面法向采用硬接触,切向采用罚摩擦,墙背摩擦角δ=φ/2=17.5°,摩擦系数f=tanδ=0.315.为模拟填土初始应力场需进行地应力平衡,荷载仅考虑土体自重.首先将填土参数赋予挡墙,将挡墙与填土联结,计算自重作用下的稳定应力场;然后将该应力场导入挡墙-填土接触模型中,作为初始应力场.
2.1.3 边界条件
对于图4所示的计算模型,墙背土体底面边界设置水平与竖向约束,右侧边界考虑为对称面,仅设置水平约束.挡墙底面设置竖向约束,通过在墙胸设置水平向的平动位移约束,实现墙体在土压力推动下的主动状态位移.
2.2 计算数据及分析
2.2.1 破裂面形状及位置
通过观察挡墙位移过程中墙背土体的塑性应变区,可得破裂面的形状及位置(见图5).由图可知,破裂面首先从墙踵产生,随挡墙位移的增加,在土体中逐渐向上延伸.墙体位移达到40 mm时,破裂面贯通,呈略微下凹的曲面.挡墙位移继续增加时,衡重台边缘开始出现塑性区.挡墙位移达60 mm时,上墙出现贯通的第二破裂面,近似为平面.
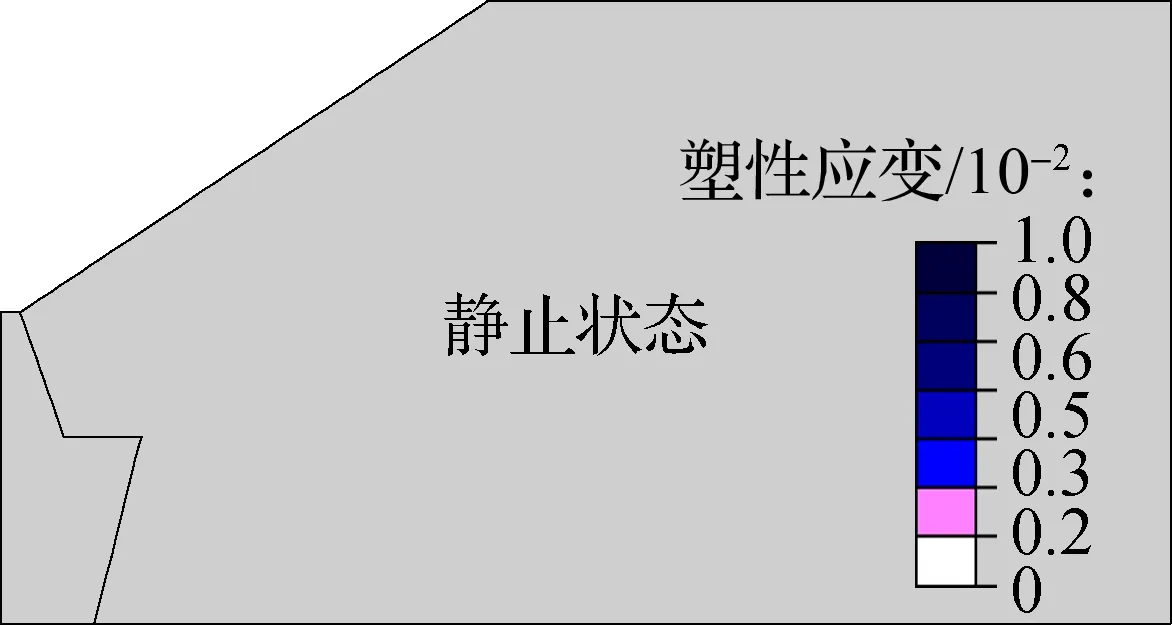
(a) 位移0 mm
挡墙及土体位移见图6.图中可观察到2条清晰的破裂面.挡墙主动位移过程中,下墙破裂面和上墙第二破裂面间的土体沿2个破裂面下滑,产生明显的水平和竖向位移.上墙背与第二破裂面之间的土体基本随挡墙一起运动,其水平位移接近挡墙位移,竖向仅有微小沉降.下墙破裂面右侧土体在挡墙位移过程中基本保持稳定.因此,2个破裂面将墙背土体划分为随动区(跟随移动)、破坏区和稳定区共3个区域.

(a) 水平位移
由图5和图6可知,土体中只出现了上墙第二破裂面和下墙破裂面,未出现上墙第一破裂面,也难以观察到第一破裂面产生的趋势.这与文献[3]中模型试验现象一致,究其原因是第一滑动面两侧土体无相对位移.文献[9]认为第一破裂面不一定能同时达到极限平衡,即全墙达到极限平衡时,该面的剪应力不一定会达到填料的抗剪强度.
开展与数值模拟相同条件的离心模型试验[16],采用1∶30的缩尺模型,墙体由不锈钢板焊接加工而成,墙背安装简支板式土压力传感器,通过步进电机和位移传感器精确控制墙体逐渐位移,从而使墙背土体逐步达到主动极限状态.试验发现,土体中先后产生下墙破裂面与上墙第二破裂面,而上墙第一破裂面始终未出现,下墙破裂面为通过墙踵的略微下凹的曲面,上墙第二破裂面为通过衡重台边缘的平面(见图7).利用摄影量测系统,追踪图钉标志点位置,根据预埋不动控制点获取土体变形信息,得到如图8所示的位移矢量图.由图可知,墙后土体同样可划分为3个区域,两破裂面间土体产生明显沉降,土体变形基本协调,未观察到形成第一破裂面的明显趋势.离心模型试验现象与有限元分析结果具有良好的一致性.

图7 离心模型试验墙背土体变形

图8 墙背土体位移矢量图
综上所述,在衡重式挡墙平动位移模式下,墙背土体达到主动极限状态时,由于潜在的上墙第一破裂面两侧土体相对位移较小,该面的剪切角未达到极限剪切角,故不会形成第一破裂面.上墙第二破裂面与下墙破裂面间的土体沿2个破裂面滑动,产生的下滑力由第二破裂面和下墙背共同承担,而传递到上墙背的土压力又与第二破裂面土压力有联系,即上、下墙土压力有直接明显的相互影响,并与上墙潜在第一破裂面上的剪切角密切相关.
2.2.2 土压力及合力作用点
墙背土体由静止状态到主动极限状态过程中,上墙背ab、下墙背co及衡重台面bc的土压力分布见图9.由图可知,上墙土压力沿墙背逐渐增大,静止土压力呈两段式折线分布,在距墙顶约1/3范围内土压力迅速增大,而在下部2/3范围内变化不明显,近似呈梯形分布;随挡墙位移的增加,土压力逐渐向三角形分布过渡,挡墙位移接近主动极限状态后基本呈三角形分布.下墙的静止土压力沿墙背缓慢增大,近似呈矩形分布;随墙体平移,墙踵处土压力首先减小,并逐渐向上传递;主动极限状态下土压力基本呈线性分布,仅在墙踵附近范围内由于土体底面受到水平约束,土压力出现一定程度的衰减.衡重台在静止状态下的土压力分布较为均匀,随挡墙位移的增加,衡重台内侧约1/2范围内的土压力变化不明显,靠近边缘部分的应力集中现象愈发显著.
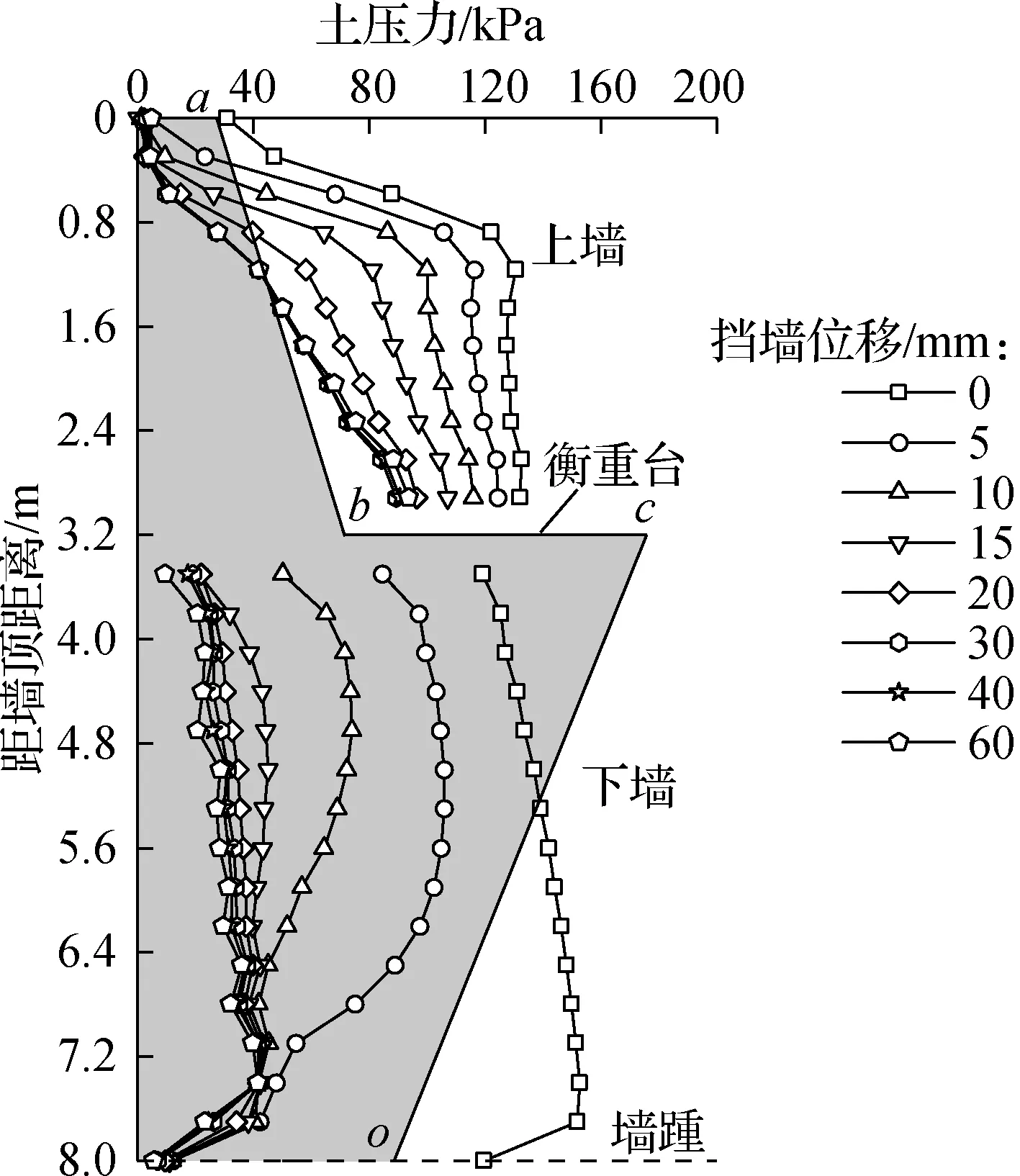
(a) 上下墙背土压力
上墙底部与下墙顶部的土压力在静止状态时比较接近,而在主动状态时存在明显差异,上墙底部的土压力远大于下墙顶部.造成这种差异的原因为:① 衡重台上土体基本随着挡墙一起运动,该土体未达到主动极限状态;② 衡重台具有较强的应力调整效应,使应力更多地向衡重台上土体集中,传递给下墙的土压力则明显减小.
根据墙背土压力分布曲线积分可得不同挡墙位移时上、下墙背及衡重台的土压力合力,从而绘制出墙背土压力合力随挡墙位移的变化曲线,结果见图10.由图可知,随挡墙位移的增加,上墙土压力合力先减小后小幅增大,下墙土压力合力逐渐减小,而衡重台土压力合力呈缓慢增大趋势.上、下墙土压力合力所占比例随挡墙位移出现明显变化,上墙静止土压力明显小于下墙,两者的占比分别为35.8%和64.2%,但上墙第二破裂面贯通时,上墙土压力占比明显增大,下墙相应减小,分别为55.9%和44.1%,这与离心模型试验[16]获得的主动极限状态时上、下墙土压力占比分别为51.4%和48.6%的结果较为吻合.鉴于衡重台的应力调整效应,墙背土压力合力随挡墙位移变化在土体达到主动极限状态后并没有趋于完全稳定,土体应力状态仍处在不断调整中,导致上墙土压力增大而下墙土压力减小,上墙土压力占全墙土压力合力的比例随挡墙位移不断提高,并且衡重台自身承受的土压力也有所增大.

图10 土压力合力随挡墙位移变化曲线
根据墙背土压力分布曲线的面域质心,可得土压力合力作用点位置(见图11).图中,e1为上墙土压力合力作用点至衡重台面的距离与上墙高的比值;ep为衡重台土压力合力作用点至衡重台边缘的距离与衡重台宽的比值;e2为下墙土压力合力作用点至墙踵的距离与下墙高的比值.对于上墙部分,静止状态时土压力呈两段式折线分布,e1≈0.45;随挡墙位移的增加,土压力合力作用点逐渐下移,e1最终稳定在0.33左右,这与传统作图法确定的合力作用点基本吻合.对于衡重台部分,土压力在静止状态时近似均匀分布,ep≈0.50,挡墙位移导致衡重台边缘处存在明显的应力集中现象,合力作用点逐渐向边缘移动,ep最终稳定在0.43左右.对于下墙部分,静止土压力沿深度增大不明显,e2≈0.48;挡墙位移初期,墙踵附近土压力衰减较快,导致合力作用点抬升,达到0.56;挡墙位移继续增加时,下墙上部的土压力逐渐衰减,合力作用点逐渐下移,e2最终稳定在0.43左右,低于传统作图法的0.47.

图11 土压力合力作用位置随挡墙位移变化曲线
2.3 有限元模拟结果与理论计算结果对比
有限元模拟结果与理论计算结果对比见表2.由表可知,对于破裂面,上墙第二破裂面倾角的模拟值小于计算值,下墙破裂面倾角基本吻合.对于土压力,第二破裂面土压力和上墙土压力的模拟值分别偏大26.7%和39.1%,下墙土压力偏小37.7%,衡重台土压力仅略大7.6%.对于摩擦角,上墙摩擦角δ1为1.29°,衡重台摩擦角δp为1.31°,均较小,与无摩擦的理论假设基本吻合;下墙摩擦角δ2为17.48°,达到极限摩擦角.对于合力作用点位置,上墙土压力合力作用点至衡重台面的距离的模拟值与计算值吻合,下墙土压力合力作用点至墙踵的距离的模拟值较计算值偏小.

表2 有限元模拟结果与理论计算结果对比
将上、下墙背及衡重台土压力矢量合成,得到全墙土压力合力E及水平、竖向分力Ex、Ey.全墙土压力合力模拟值与计算值接近,比值为1.01.对于挡墙整体稳定性,由于土压力水平分量略小于计算值,而竖向分量略大,采用计算值进行抗滑动稳定性检算偏于安全.全墙土压力对墙踵的倾覆力矩和稳定力矩见表3.由表可知,模拟值与计算值接近,对挡墙的抗倾覆稳定性影响较小.
表3 全墙土压力力矩 kNm

表3 全墙土压力力矩 kNm
土压力力矩模拟值计算值比值倾覆力矩M01 249.281 235.931.01稳定力矩My872.19834.421.05
模拟结果与理论计算结果的差异主要表现为上墙土压力明显偏大而下墙土压力偏小,对上墙与衡重台连接处的薄弱截面强度验算非常不利.这可能是实际工程中衡重式挡墙常出现上墙拉裂破坏的重要原因.
3 土压力计算修正模式
3.1 计算图式及公式推导
通过有限元分析,上墙第一破裂面没有形成是造成土压力模拟值与计算值存在明显差异的主要原因.第一破裂面未形成的实质是相应区域的剪应力未达到抗剪强度,故假设第一破裂面上反力R1与法线的夹角ζ∈[0,φ],据此提出衡重式挡墙土压力计算修正模式,将图1中R1对应的偏角φ改为ζ.而ζ取值将影响分配到下墙背的土压力E2和第二破裂面的土压力E′,进而通过衡重台上土体abcd的力传递作用,影响上墙土压力E1.
边界条件不同,推导出的土压力计算公式形式也不相同.以衡重式路堤挡墙第一破裂面交于路基面的情况为例,推导产生第二破裂面时上、下墙的土压力计算公式[3-4].
图12为第二破裂面及上墙土压力计算示意图。图中,H′为上墙与边坡高度之和;W1和W2分别为土体acd和abc的质量;l1和l2分别为线段ek的水平和垂直投影长度.根据图中破裂棱体cdeg的静力平衡条件,可得作用在第二破裂面上的水平土压力E′x为
(3)
式中
(4)
h″=H1secα′cos(α′-λ)
(5)
式中,h″为辅助线cj的长度;γ为填土密度.
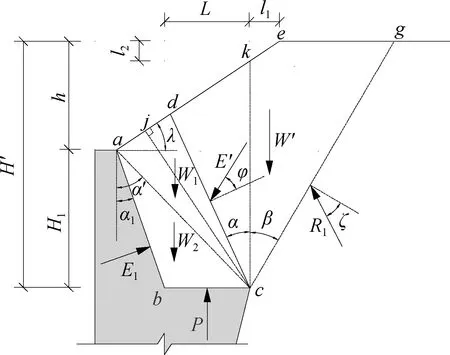
图12 第二破裂面及上墙土压力计算示意图
将式(3)代入式(1)和(2),联立求解可得
(6)
式中
S1=cotζcot(φ+ζ+λ)
根据式(6)可得2个β根值,有效根即为第一破裂面倾角,第二破裂面倾角α可由下式确定:
tan(α-λ)=cot(φ+λ)-

(7)
将α和β代入式(3),可求得E′x为
(8)
进而便可求得第二破裂面土压力E′和竖向土压力E′y.
根据图12中衡重台上土体abcd静力平衡条件,可求得作用于上墙土压力E1和衡重台土压力P.将土体abcd沿假想墙背分割为2个三角形,由几何关系得土体质量W1和W2,即
(9)
由于P和W的方向均为竖向,根据力多边形可得
E1=E′xsecα1
(10)
P=E′y+W-E′xtanα1
(11)
根据破裂棱体cgmo的静力平衡条件,可得作用在下墙背的土压力E2为
(12)
式中
ψ=φ+δ2-α2
(13)
(14)
W″=γ(A0tanθ-B0)
(15)
根据几何关系可得
(16)
(17)
由dE2/dθ=0得
(18)
(19)
同样,根据式(18)可得2个θ根值,有效根即为下墙破裂面倾角θ,代入式(12)中可得下墙土压力E2.
3.2 第一破裂面的剪切角发挥系数
根据衡重式挡墙土压力计算修正模式及破裂角和墙背土压力计算公式,定义上墙第一破裂面上的剪切角ζ与土体内摩擦角φ的比值为剪切角发挥系数η=ζ/φ,且η∈[0, 1].按照递减原则取不同η值进行计算,结果见表4.

表4 有限元模拟结果与修正后理论计算结果对比
由表4可知,随着η的减小,α逐渐减小,β逐渐增大,θ变化不明显.β增大到一定程度将导致2个破裂面发生交叉,即可作为η取值的下限.本算例条件下η最小取值约为0.80.
进一步分析发现,破裂棱体cdegmo体积随η的减小基本不变,全墙土压力合力E变化不大;上墙第一、二破裂面间棱体cdeg的体积显著增大,下墙棱体cgmo明显减小,导致E1和P增大,而E2减小.当η=0.85时,修正后计算值与模拟值最接近,各项比值均位于[0.86, 1.02]区间内,平均值为0.97;此时,E1的模拟值相较于传统计算值增大37.5%,E2的模拟值减小27.4%,说明η值对上、下墙土压力分配影响显著.以η= 0.85时第一破裂面倾角β=45.4°为参考,在有限元模型中以该角度建立第一破裂面路径,沿路径提取15个节点的水平应力σx、竖向应力σy及剪应力τxy=τyx,根据Mohr应力圆可得各节点在第一破裂面上的法向应力σβ和剪应力τβ,从而求得ζ和η,η∈[0.51, 0.96],且η的平均值为0.83,与0.85取值接近.
3.3 多因素正交试验分析
采用正交试验对影响η值的多因素进行综合分析.根据衡重式挡墙特点,从路堤边坡形式、填料性质和挡墙尺寸3个方面选取6个因素,包括边坡高度、边坡坡度、内摩擦角、衡重台宽度、挡墙高度及上墙高占比,每个因素包含3个水平(见表5).

表5 正交试验因素及水平
基于正交试验设计,采用六因素三水平正交表,制定如表6所示的试验方案.首先,每组试验按2.1节方法建模计算,并获得模拟值.然后,由土压力计算修正模式,按照3.2节,以上墙和衡重台土压力修正后计算值与模拟值偏差最小为原则,确定η值.分析表明,相较于修正值,上墙土压力模拟值平均偏大3.1%,衡重台土压力模拟值平均偏小-2.4%,下墙土压力模拟值平均偏小-6.2%;相较于规范值,上墙土压力模拟值平均偏大59.2%,衡重台土压力模拟值平均偏大7.8%,下墙土压力模拟值平均偏小28.0%.由此可见,采用修正模式获得的土压力值更接近模拟值,较规范方法有显著改善.

表6 正交试验方案及数据
采用极差分析法,将η值按各因素不同水平分别计算平均值并求极差,可直观判断各因素对η值的影响程度,结果见表7.由表可知,在6个因素中,路堤边坡高度h=0~8 m时,η由0.36增至0.83,其余因素的3个水平对应的η值较接近,波动范围较小.根据极差大小,可排列出各因素对指标η影响程度由大到小依次为:边坡高度、衡重台宽度、边坡坡度、上墙占比、挡墙高度、内摩擦角.

表7 极差分析
进一步根据方差分析法,取显著水平临界值0.05判断各因素显著性,结果见表8.由表可知,仅边坡高度的显著性水平小于0.05,说明边坡高度对η值影响显著,其余因素均不显著.显著性水平排序与极差分析结果基本一致.

表8 方差分析
因此,采用基于土体破裂面剪切状态的修正方法计算衡重式挡墙背土压力时,可根据边坡高度h来确定η值,由表7数据可得拟合公式为
η=0.841-0.478e-0.505h
(20)
根据式(20)确定的η拟合值,计算得到土压力值,与正交试验的修正值间存在一定偏差(见表9).由表可知,上、下墙背和衡重台的土压力值的偏差均在20%以内,平均偏差分别为0.2%、-1.0%和0.7%,说明整体偏差较小.

表9 η拟合值的土压力相对偏差 %
4 结论
1) 墙背土体在衡重式挡墙平动位移下达到主动极限状态,根据变形特征可分为随动区、破坏区和稳定区.3个区域土体存在明显变形差异,导致产生过衡重台缘的上墙第二破裂面和过墙踵的下墙破裂面,而破坏区范围的土体变形基本协调,规范方法假设的上墙第一破裂面难以形成.
2) 上墙第一破裂面剪切角发挥程度对破裂棱体的体积影响较小,全墙土压力合力变化不大,但会显著调整上、下墙土压力分配比例,引发上墙土压力增大和下墙减小的现象.计算表明,相较于规范值,上墙土压力模拟值平均偏大59.2%,下墙土压力模拟值平均偏小28.0%.
3) 通过引入上墙第一破裂面剪切角发挥系数η,建立基于土体破裂面剪切状态的衡重式挡墙土压力计算修正模式,较好地反映了土体破裂面特征及土压力在上、下墙间的分配关系.分析表明,η值主要受路堤边坡高度h影响,可采用关系式η=0.841-0.478e-0.505h确定.

