发动机喷嘴光学测量中光学畸变的修正方法

丰雷, 丁星星

（1.海装广州局驻重庆地区第二军事代表室，重庆 402260；2.西南技术工程研究所，重庆 400039）

近年来，在发动机燃烧和喷雾研究领域，光学测试技术的应用越来越广泛，例如粒子图像测速技术、激光多普勒测速技术、光学层析技术以及高速摄影技术等，这些都是非接触的光学测量技术，能够比较准确地测量复杂流动现象。这些技术应用在测量发动机喷嘴内部流动及雾化情况时，由于透明固壁对光线的折射作用而导致测量结果存在误差，故而，使得光学测量技术在曲面形状的透明固壁上应用受到限制。

管壁形状对测量精度的影响可由Klein 的试验结果进行分析，Klein 等人运用光线追踪技术[1]分析了透明管壁对光线传播的影响，结果表明不同圆管壁厚对光学测量中光线的传播会产生一定的影响，测量区域内外不同介质也会对光学测量中光线传播产生影响。从光源发出的平行光线经过圆管的透明管壁后，光线不再保持平行而是发生偏折，即光线的波阵面发生扭曲，从而导致被测区域的成像性能降低，发生光学畸变[2]。光学畸变的主要原因在于光线在不同折射率材料分界面上传播过程中会发生折射[3]。因此，要想提高非接触的光学测量中被测区域的成像性能，就需要采取一定的光学修正措施，如改变透明曲面状固壁的外壁形状可使光学畸变得到较好改善。Benjamin 等人[4]就是通过直接改变圆管的外壁形状，达到了减小光学畸变的目的，该方法简单实用，能够解决圆管的透明管壁带来的光学畸变问题。但是，Benjamin 等人的工作仅限于修正圆管的光学畸变，并且是简单的圆管，对于其他类型曲面形状透明固壁内的流动情况就不能实现较好的光学修正。本文以Benjamin 的研究工作为基础，进行扩展性研究，使其更具普遍性，以探讨解决在任意曲面形状透明固壁带来的光学畸变问题。

一、理论基础

目前，光学分析的基础理论主要有量子光学、物理光学（波动光学）和几何光学[5]。这些理论都有不同的适用范围。本文将应用物理光学（波动光学）和几何光学理论对光学畸变问题进行分析。早在1690年惠更斯[6]就提出：光线总是垂直波阵面，即光线的方向余弦总是与波阵面的空间导数一致的，如图1 所示。所以，当光线从一种介质入射到另外一种折射率不同的介质[7]，出射光偏折的程度表征了出射点处波阵面倾斜程度。

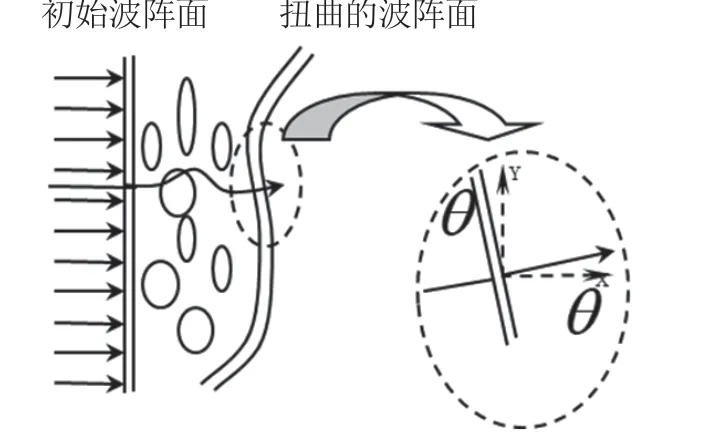
图1 光线在介质中的传播过程[4]

同样地，还可引入费马原理[8]中光程的概念对波阵面进行描述，理想情况下平面光源发出的光在折射率相同的透明介质传播时波阵面应该仍然保持为平面。如果波阵面发生扭曲，那么在一个几何平面上各点的总光程（OPL）应该不同，即同一几何平面上各点的总光程不同，就意味着波阵面发生扭曲。为了描述波阵面的扭曲程度，引入一个光程偏差（OPD）的概念，即各点总光程与平均光程之间的差值。如果波阵面未发生扭曲，那么一个几何平面上各点的光程偏差应该为0。总光程和光程偏差进行数学描述为：

式中，OPL 为A、B 两点之间的总光程；OPD 为几何平面上一点的光程偏差；OPLave为几何平面上各点的总光程的平均值；n（s）为沿光传播路径各个位置的折射率。

二、光学修正

与Benjamin 等[4]在圆管光学修正中所作的假设类似，本文假设平面光源与z=0 平面重合；光源平面上各点发出的光平行Z 轴传播，如图2 所示。调整实际测量装置的坐标方位可以使光源平面以及光源发出的光的传播方向与上述假设一致，所以所述的假设具有普遍性。从平面光源发出的光在流体、任意曲面状透明固壁下以及外界空气传播过程，如图2所示。光源平面上一点（x0，y0，z0）发出的光对应的光线为Ray1，首先传播到透明固壁的内壁（即与流体接触的壁面）（x1，y1，z1）处，经第一次折射后进入透明固壁内，对应如图2 中所示的光线Ray2。此时x1、y1和z1 满足以下关系：

过透明固壁内壁点（x1，y1，z1）作切平面P1，此切平面代表了内部流体与透明固壁的分界面。沿用圆管光学修正中光线的表示方式，用单位向量r1表示光线Ray1 的方向，用向量r2表示光线Ray2 的方向。在平面P1上根据斯涅尔[9]折射定律可得，向量r1、向量r2以及（x1，y1，z1）处法线向量N1共面，并且所在平面与切平面P1 垂直，根据向量的关系有下式成立：

式中，n1和n2 分别表示内部流体的折射率以及透明固壁的折射率；θ1为入射角，即（x1，y1，z1）处法线向量N1与向量r1之间的夹角；θ2为折射角，即（x1，y1，z1）处法线向量N1与向量r2之间的夹角。

根据式(5)和式(6)两个方程并不能确定向量r2。为此假设向量r2为单位向量，即|r2|=1，再通过迭代计算得出可能的单位向量r2。合理利用向量r1、向量r2以及（x1，y1，z1）处法线向量N1位置的逻辑关系，就可确定精确的单位向量r2。

进入透明材料内的光继续传播直到透明材料外壁（x2，y2，z2）处，经第二次折射传播到外界大气中，如图2 所示光线Ray3，用单位向量r3表示。

图2 光在流体、任意曲面状透明固壁下以及外界空气传播示意图

进入透明材料内的光继续传播直到透明材料外壁（x2，y2，z2）处，经第二次折射传播到外界大气中，如图3 所示光线Ray3，用单位向量r3表示。

图3 透明喷孔光学测量装置

为减小光学畸变，光学修正后光线Ray3 必须保证与Ray1 平行。采取的修正措施依然是改变透明固壁的外壁的形状，为此需要计算透明材料外壁在（x2，y2，z2）处的法线向量N2以及x2、y2和z2。由于光线Ray3 与Ray1 平行，所以有：

三、计算结果及分析

根据2 节中提到的方法，本文编制了迭代计算程序，求解某透明喷嘴喷孔外壁各点的坐标位置及其法线向量，其用于测量的透明喷孔及试验装置如图3 所示，其喷孔为圆管形状。考虑到圆管形状的特殊性，假设单位向量r1=（1，0）T，管内流体为折射率为1.33 的水，管壁的材料为折射率1.49 的亚克力，管外介质为折射率为1 的空气。管内径为60 毫米，总光程为M 取值为从点（0，0）发出的光线传播到点（40，0）的总光程值，即取值为54.80 毫米。求解得到管子外壁各点的坐标位置及此处外壁的法线向量后，进行插值便可得到外壁的外形。进行光学修正后，圆管的外形变成如图4 中所示，其中虚线代表圆管原外形。

图4 光学修正后圆管的外形图

据比较，修正后的方法的结果与使用Benjamin等人[4]的修正方法得到的结果一样。由此说明本文所述光学修正一节中提到的修正方法可靠，能够用该修正方法修正任意曲面状透明固壁引起的光学畸变，使从透明固壁中传播出来的光与光源发出的光平行，即波阵面几乎不发生扭曲，减小光学畸变，如图5 所示。

图5 光学修正后光线的传播图

但是管壁传播出来的光线和光源发出的光线并不共线，所以测量还是有误差的。图6 给出了Y 轴上不同位置的光源发出的光线经管壁的两次折射后，光线Ray3 与光线Ray1 在Y 轴方向的位置偏差。可见光源发出的光越是远离轴心，光线Ray3 与光线Ray1 在Y 轴方向上的偏差越大。对此的修正方法可以采用光的可逆性，将修正后管子的一半反对称地置于测量区域与记录装置之间，如图7 所示。可见经此处理后光线Ray3 与光线Ray1 在Y 轴方向的位置几乎减0。

图6 光线Ray3与光线Ray1之间在Y轴方向的位置偏差

同样地，对于任意曲面状透明固壁，经此方法修正后，从透明固壁中传播出来的光和光源发出的光并不共线，所以测量还是有误差的。但是根据光的可逆性，只需将修正之后的透明固壁反对称地放置在所测区域与记录装置之间，就可保证传播出来的光和光源发出的光共线，从而大幅提高测量结果的精度。图8为利用光学修正一节中提到的方法对该透明喷嘴喷孔进行的光学修正后的效果图，同时图中也显示了经过光学修正后光源发出的光线的传播途径。从图7 可以看出，经过光学修正后，由管壁传播出来的光线和光源发出的光线平行，波阵面几乎不发生扭曲，光学畸变程度减小。

图7 出射光线和光源发出的光线共线示意图

图8 对球面固壁进行光学修正后光的传播示意图

四、结束语

本文首先举例说明光学测量过程中，曲面的折射作用对光学测量的影响。分析得出如不采取修正的手段，光在内部流体和曲面状透明固壁之间传播后会发生偏折，引起波阵面发生扭曲，造成光学畸变。该光学畸变极大地降低光学测量的成像性能，降低光学测量的精度，限制了光学测量的使用区域。为此，本文对光学修正方法进行修正，并进一步地将该光学修正方法扩展到适用于测量固壁为任意曲面状透明固壁的内部流动。之后将所设计的修正后的光学修正方法应用于圆管，其结果与圆管光学修正方法的结果吻合良好，所以本文设计的扩展光学修正方法是有效的，并具有实际意义。虽然经过光学修正之后，波阵面的扭曲减少，但是由于从透明固壁传播出来的光与光源发出的光并不共线，所以由此引起误差仍然存在。不过根据光的可逆性可知，如果在所测区域的透明固壁外壁面和光学记录装置之间再额外添加一块与测量区域固壁形状完全一样的透明固壁，并反对称放置，则经过该额外添加透明固壁传播出来的光线将与光源发出的光线完全共线。

通过本文所提出的光学修正方法能够大幅提高各种光学测量的精度，并将这种修正方法的应用范围扩大到任意曲面的透明固壁。