角域多信息熵融合算法的EHA柱塞泵滑靴副状态评估方法
孙红梅, 王 杰, 王志伟, 刘思远
(1.北京电子科技职业学院, 北京 100167;2.燕山大学 河北省重型机械流体动力传输与控制重点实验室, 河北 秦皇岛 066004;3.先进锻压成形技术与科学教育部重点实验室(燕山大学), 河北 秦皇岛 066004)
引言
EHA采用闭式回路容积控制的静液传动方式,通过伺服电机直接调节泵轴转速控制其输出流量,实现变功率传输,是航空航天、机器人及轨道交通等重要领域的新型作动器系统[1]。EHA柱塞泵是该执行器的核心动力元件,在变转速极端工况下,其运行状态好坏直接关系到EHA整机的性能。因此,对EHA柱塞泵进行有效的健康状态评估对于EHA整机的安全稳定运行至关重要。
近年来,国内外在柱塞泵健康状态评估研究领域对普通柱塞泵的研究成果颇丰。在国外,CASOLI P等[2]提出了一种基于振动信号检测柱塞泵的健康状态解决方案。 BEDOTTI A等[3]采用数据采集和特征提取相结合的数据驱动方法,基于循环平稳性理论对加速度信号进行分析,准确识别泵的故障。MO J O等[4]开发了流固耦合和自定义函数技术,研究阀型对柱塞泵性能改善的影响。在国内,陈远玲等[5]基于Archard方程和流-热-固耦合方法,建立一种适用于高速高压条件下的航空柱塞泵配流副摩擦磨损预测模型来提高配流副磨损寿命。洪晓艺等[6]提出基于局部均值分解信号重构和支持向量机的柱塞泵故障诊断方法,提高柱塞泵故障诊断效率。魏晓良等[7]研究了一种融合振动信号频谱分析和卷积神经网络的诊断方法,能准确地识别出柱塞泵的空化故障等级。经调研发现,绝大多数研究是在柱塞泵定转速工况条件下开展的。
另外,多信息融合方法也常用于机械装备健康状态评估研究,李志远[8]采用多传感器信息融合的方法评估了柱塞泵的健康状态,得到了较好的效果。刘洋等[9]针对薄壁机器人轴承提出了基于信息融合的评估方法。袁岳等[10]运用多维信息融合对变压器的运行状态进行了评估。
有研究表明,变转速工况下旋转机械的故障特征与定转速工况相比完全不同,基于定转速工况的评估方法在变转速工况下并不适用,因此,若要对EHA柱塞泵进行有效的状态评估就必须探索新的评估理论和方法。
本研究模拟了EHA柱塞泵恒压变转速极端工况,人为制造了滑靴外边缘偏磨磨损故障,并开展了状态评估研究。结合阶比分析与信息熵理论提出“角域信息熵”新概念,将时域振动信号反映出的能量表征信息转化成角域信息熵;在角域尺度下提取奇异谱熵、功率谱熵、能量熵、特征空间熵、边际谱熵5种信息熵表征参数构建评估指标体系;结合BP神经网络和D-S证据理论构建基于角域多信息熵融合的滑靴磨损状态评估模型;通过状态评估测试试验,验证新方法的有效性及评估效果。
1 滑靴外边缘偏磨磨损机理
柱塞泵滑靴周向运动引起的离心力矩以及随缸体旋转所产生的摩擦力矩,在柱塞腔高低压油液切换过程中均会对滑靴相对斜盘表面产生倾覆作用,使滑靴底面与斜盘表面形成一定的夹角,滑靴外边缘处油膜变薄,滑靴与斜盘极易发生直接接触而导致滑靴副磨损。变转速极端工况条件使滑靴倾覆加剧,滑靴倾斜角度增大,动压效应产生的抗倾覆力矩对滑靴的平衡作用减弱,滑靴副局部最小油膜厚度变薄,滑靴与斜盘的接触应力增大,增加了滑靴发生外边缘偏磨磨损故障的概率[11-12]。
设滑靴在周向运动产生的离心力为FωS,滑靴与油膜之间产生的黏性摩擦力为FTS,离心力与黏性摩擦力产生的离心力矩和摩擦力矩分别为MωS和MTS,对滑靴进行受力分析,如图1所示,可推导出滑靴所受离心力和离心力矩分别为[13]:
FωS=mSrω2
(1)
MωS=FωSlSG
(2)
滑靴所受摩擦力和摩擦力矩分别为:
(3)
MTS=FTSlG
(4)
式中,mS—— 滑靴质量
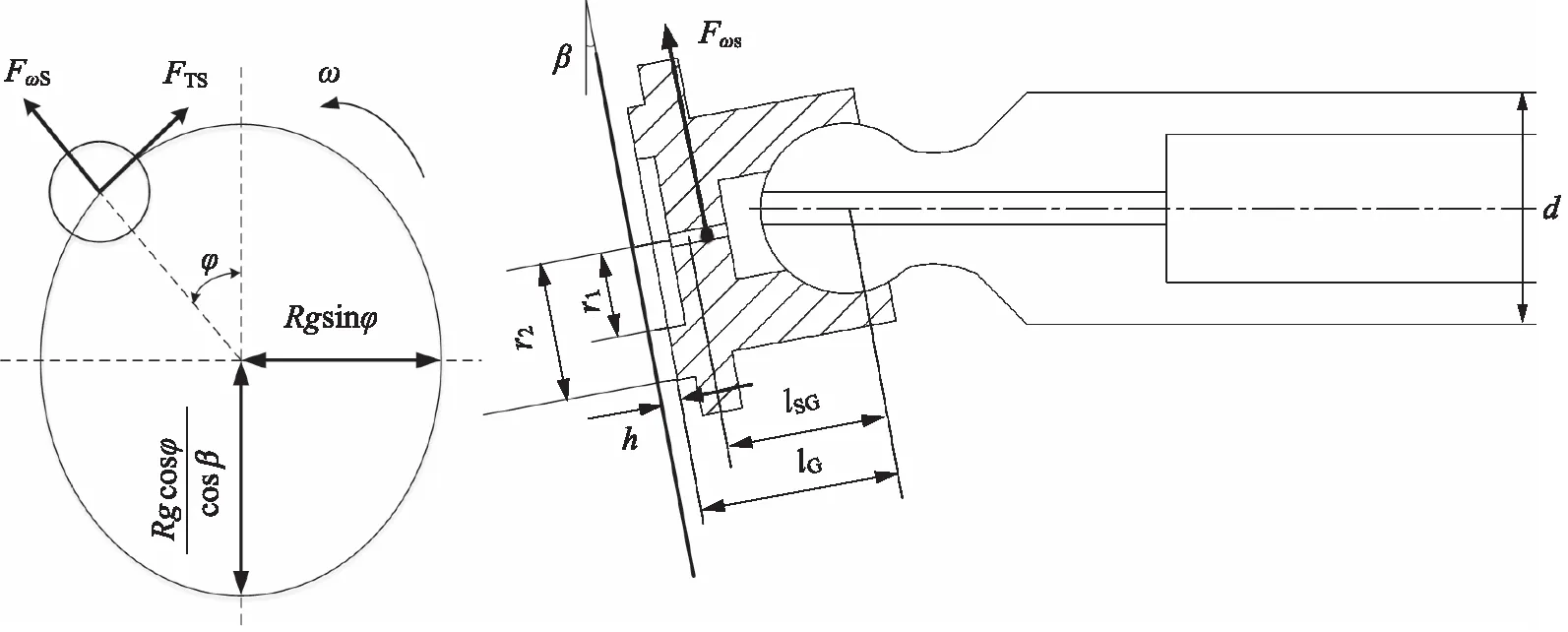
图1 滑靴受力分析Fig.1 Force analysis of slipper
r—— 滑靴底面任意一点与滑靴中心的半径
ω—— 滑靴球窝中心点运动角速度
r1—— 滑靴密封带内径
r2—— 滑靴密封带外径
μ—— 油液黏性系数
R—— 柱塞的分布圆半径
h—— 滑靴底面油膜厚度
lSG—— 滑靴中心到柱塞球头中心的距离
lG—— 滑靴底面到柱塞球头中心的距离
由于滑靴倾覆作用使滑靴对斜盘的压紧力偏离滑靴轴线,在此力所引起的摩擦力作用下,滑靴在运动中会绕自身轴线做旋转运动,转动的快慢取决于旋转摩擦力的大小,因此,外边缘偏磨磨损程度沿滑靴底面周向的差异性不大,实际磨损情况如图2所示。由此,可将外边缘偏磨磨损形状近似假设为圆周形。

图2 滑靴外边缘偏磨磨损Fig.2 Slipper outside edge wear diagram
2 角域信息熵及表征参数
信息熵是对信号或系统状态不确定性程度定量描述的一种有效测度指标,因此可以用信息熵对旋转机械健康状态进行度量。
当给定信息系统K=(U,A)P⊆A,设U为一论域,P为U上的一个等价关系,令U/P={X1,X2,…,Xn},基于U/P构建的概率分布为:
P(Xi)=|Xi|/|U|,1≤i≤n
则属性集P的知识熵,也称信息熵[14]为:
(5)
目前,在应用信息熵进行旋转机械故障诊断和状态评估研究时,表征参数提取一般为定转速周期性时域信息,而对于变转速非周期性的时域信息则需要转化成周期性信息才能进一步处理,因此,信息熵的概念和表征参数需要重新定义。
2.1 角域信息熵
针对变转速工况等时间间隔采样信息不确定程度难于表达的问题,将时频阶比分析方法引入到信息系统的熵理论中,提出能够量化描述等角度采样信息系统不确定性的“角域信息熵”物理量,并由此可以得到相应的奇异谱熵、功率谱熵、能量熵、边际谱熵和特征空间熵5种表征信息。
将原始时域信息转化为角域信息的处理流程如图3所示,具体实现步骤为:首先对原始振动信号做EEMD分解和Hilbert包络解调,并实施降采样处理;利用小波族带通滤波方法对降采样后的信号进行滤波,并利用式(6)进行阶比重采样,采样阶比为:
(6)
式中,θ—— 相邻的两个采样点之间参考轴转过的角度。阶比可表示为基准轴每转一周发生的循环振动次数。
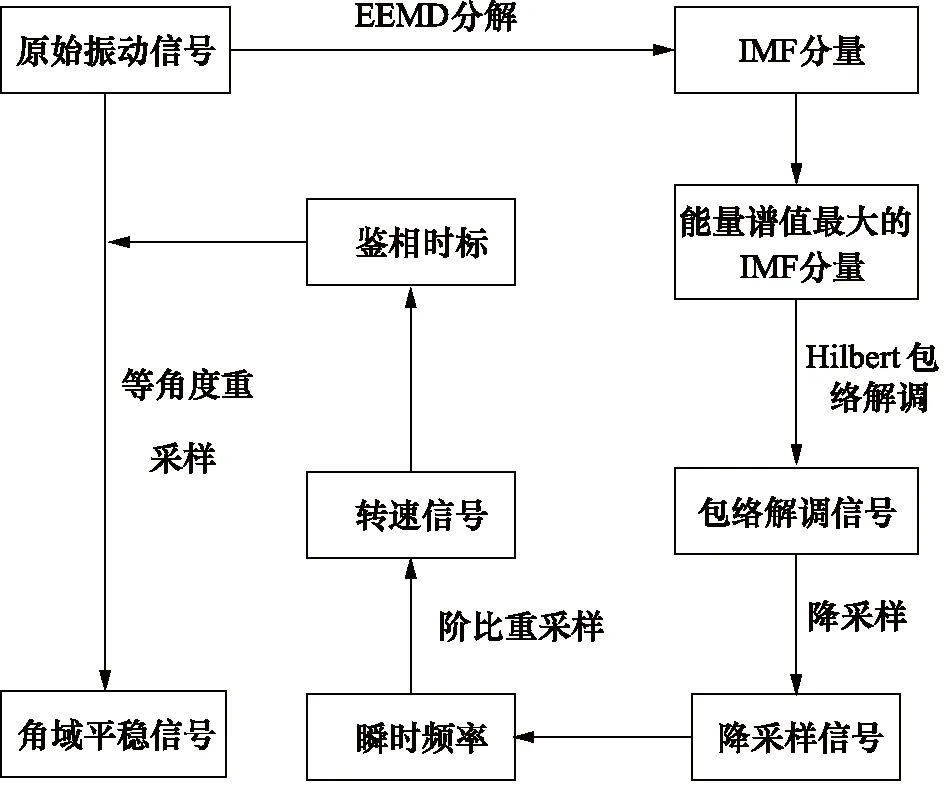
图3 信息处理流程图Fig.3 Flow chart of information processing
通过式(7)求解转速拟合曲线的积分方程获得鉴相时标Tm:
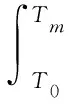
(7)
式中,t—— 时间
k—— 段数序列号
m—— 时标序号
Δθ—— 等角度采样的采样间隔
T0—— 速度拟合曲线的初始时间
其中,Rt(t)=ak+bk+ckt2。ak,bk,ck为拟合方程的多项式系数。对式(7)进一步推导,可得到等角度采样的鉴相时标Tm序列方程:
(8)
用上述方程求得的鉴相时标对原始振动信号进行式(9)的Lagrange插值重采样,将等时间间隔的非平稳信号转化成等角度间隔的平稳信号。

(9)
式中,ti—— 信号x(t)数据中时间坐标小于等于Tm的最近时间点
2.2 奇异谱熵
给定角域信号离散时间序列x=[x1,x2,…,xN],以(M,1)的模式窗口将x顺序分为N-M段模式数据,这些数据构成了一个模式矩阵:
其中,M为选定分析空间的长度。
对矩阵A进行奇异值分解。假设计算结果的奇异值为δ1≥δ2≥,…,≥δM,则{δ1,δ2,…,δM}构成了振动信号的奇异值谱。由此可定义角域信息的奇异谱熵为:
(10)
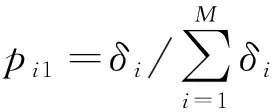
2.3 功率谱熵

(11)
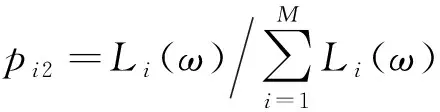
2.4 能量熵
设E=[E1,E2,…,Ej,…,Em]为给定角域信号x=[x1,x2,…,xN] 在m个尺度上的小波能量谱,因此在多尺度域上形成了对信号能量的一种划分。
其中第j尺度下信号能量为该尺度小波系数的平方和:
(12)
其中,n1为采样点长度;k=1,2,…,n1;Dj(k)为第j尺度的小波重构系数。因此可以定义角域小波能量熵为:
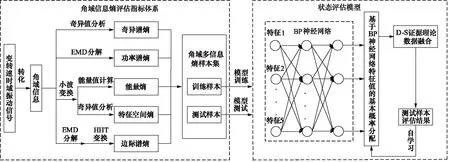
图4 角域多信息熵融合的状态评估方法Fig.4 Multi-information entropy fusion state assessment method in angular domain
(13)

2.5 特征空间熵
将给定的角域信号x=[x1,x2,…,xN]经过连续小波变换,得到m个尺度下的小波分解系数D=[D1,D2,…,Dm],由此可与角域信号x构成一个m×n的小波分解系数矩阵Dm×n。根据信号奇异值分解理论对Dm×n进行奇异值分解得到奇异值谱{δj},由此角域空间特征熵为:
(14)
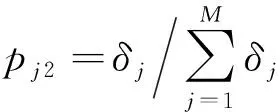
2.6 边际谱熵
将给定的角域信号x=[x1,x2,…,xN]经过EEMD分解为N个子频带分量{c1,c2,…,cN},由此可通过希尔伯特变换求得第i个分量的瞬时幅值函数ai(Tm)和瞬时相位函数φi(Tm),如式(15)~式(17)所示:
(15)
(16)
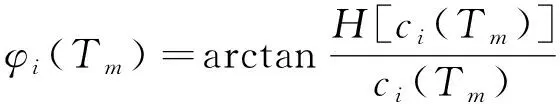
(17)
由瞬时相位函数可求出瞬时频率:
(18)
则原始信号x=[x1,x2,…,xN]的Hilbert谱表示为:
(19)
则其对应的边际谱为:

(20)
由此定义边际谱熵为:
(21)
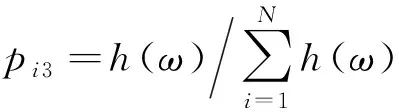
3 角域多信息熵融合的状态评估方法
建立角域多信息熵融合的状态评估模型,并给出具体求解方法和状态评估流程,如图4所示。详细步骤如下:
(1) 采用本研究提出的“角域信息熵”新概念将试验采集的变转速工况时域振动信号能量表征信息转化为角域信息;
(2) 提取角域尺度下的奇异谱熵、功率谱熵、能量熵、特征空间熵、边际谱熵5种信息熵表征参数构建评估指标体系;
(3) 采用BP神经网络对5种信息熵表征参数进行概率分配,并通过D-S证据理论方法进行特征信息决策融合,建立基于滑靴磨损机理的柱塞泵状态评估模型;
(4) 设计试验方案,利用测试样本验证评估模型的有效性和检测评估结果的准确性。
4 试验分析
本试验依托于燕山大学河北省重型机械流体动力传输与控制重点实验室,在柱塞泵恒压故障模拟及状态检测试验台上完成。试验以国产CY型轴向柱塞泵作为被试泵,采用定压油源系统,利用变频器调节电机转速模拟EHA柱塞泵的变转速工况,泵端盖装加速度传感器采集滑靴外边缘偏磨磨损故障振动信号,试验台如图5所示。

图5 液压泵故障模拟及状态检测综合试验台Fig.5 Hydraulic pump fault simulation and state detection comprehensive test bench
采样频率为10 kHz,采用斜坡信号类型,以3 s为周期进行电机升降速控制,前半段由1500 r/min下降至900 r/min,后半段由900 r/min上升至1500 r/min,1个周期内的转速n时域波形如图6所示。
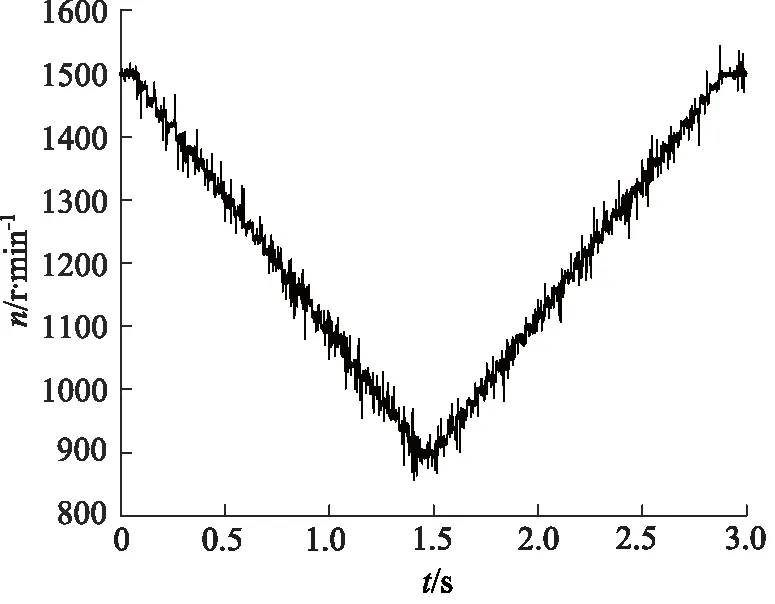
图6 转速信号模拟的时域波形图Fig.6 Time domain waveform of rotating speed signal
人为制作滑靴外边缘全周偏磨磨损故障,设计出如图7所示的滑靴外边缘磨损轮廓。根据滑靴副设计理论[15],可将H设定为一定值(H=0.5 mm)。依据柱塞泵滑靴外边缘偏磨磨损机理知识,设计和加工出单柱塞滑靴不同磨损程度的3种故障样件,可将磨损程度由小到大进行排列并根据磨损量C的取值进行阶段划分:正常样件对应正常阶段(C=0 mm),磨损1(C=1 mm)对应失稳阶段(C∈(0 mm,1.2 mm]),磨损2(C=1.5 mm)、磨损3(C=2 mm)对应失效阶段(C∈(1.2 mm,2.5 mm]),采用4种不同状态的滑靴描述故障状态的发展过程,如图8所示。采用每间隔3 s截取1段信息制作1个样本数据的方式,构建评估指标敏感性分析样本集以及状态评估模型训练样本集。

图7 滑靴外边缘磨损轮廓示意图Fig.7 Wear profile of outside edge of slipper

图8 滑靴外边缘偏磨磨损样件Fig.8 Wear condition of the slipper outer edge
采集滑靴在4种工作状态下的泵端盖振动信号,时域波形如图9所示。由图可知,转速降低,加速度a的振动幅值相应减小,随着滑靴磨损程度的增加,振动幅值也随之增大,可见,振动信号的时域波形只能定性反映磨损变化的特征,无法定量描述滑靴磨损故障状态的发展程度。
5 状态评估
5.1 评估指标的敏感性分析
每种状态信号截取30段信息。利用角域信息熵新概念和5种表征参数提取方法,计算滑靴在4种工作状态下共120组表征参数的特征值, 将3种磨损与正常状态特征值比较,分析表征参数对滑靴磨损程度的敏感性,其结果如图10所示,其中η表示样本数。由图可知,5种表征参数对滑靴不同程度的磨损都有明显的区分且敏感性较好。随着磨损程度的增加,5种表征参数特征值分布区域均有明显的减小趋势,其中功率谱熵和特征空间熵对滑靴磨损程度的敏感性表现更为明显。
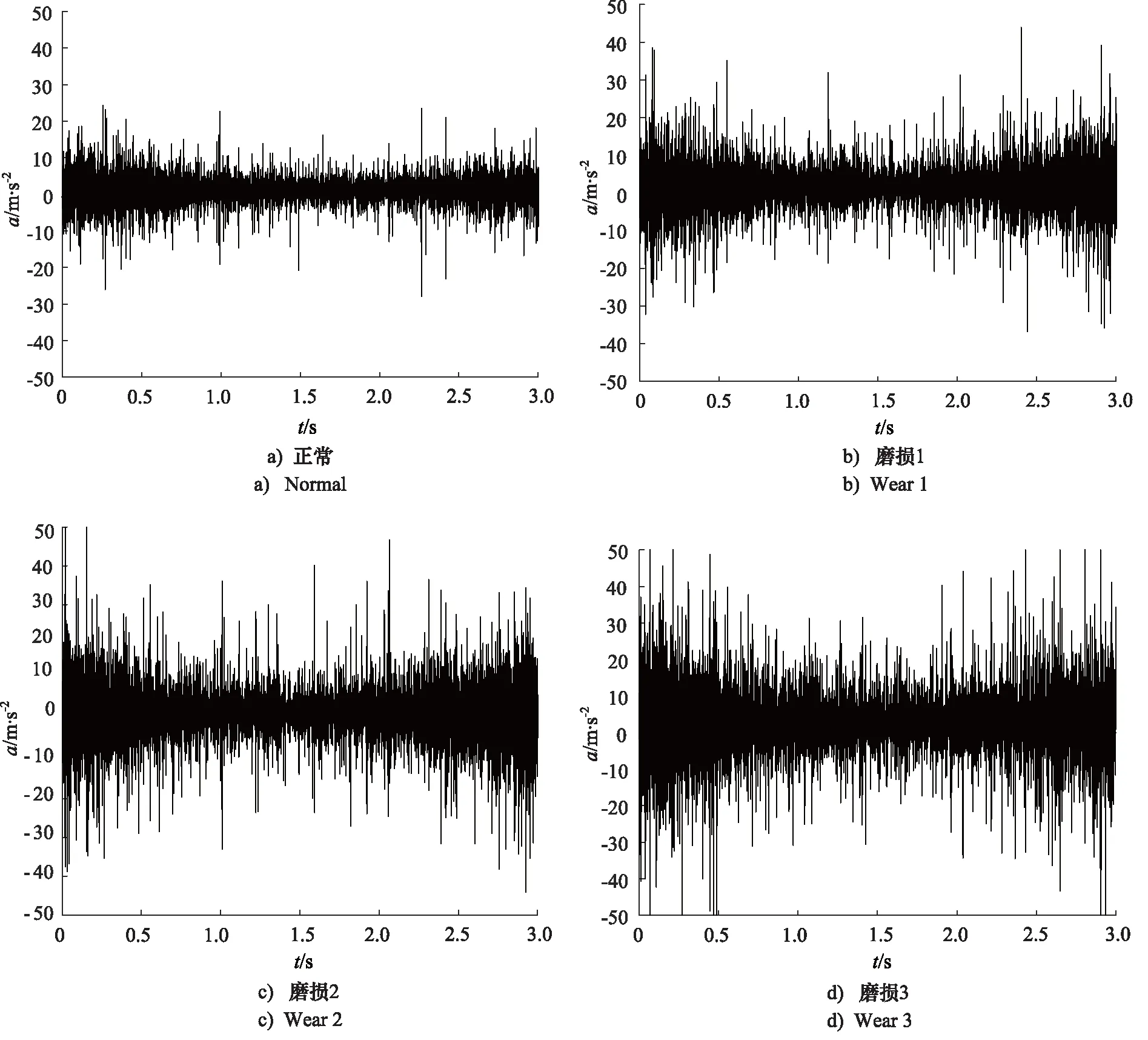
图9 振动信号时域波形图Fig.9 Time domain waveform of vibration signal
通过计算可得出滑靴不同磨损程度角域信息熵表征参数平均特征值, 如表1所示。可看出随磨损程度的增加,各表征参数平均特征值有明显的减小趋势,且磨损程度越大表征参数平均特征值越小,从而反映出的故障特征信息量越大,越容易确定故障程度。由此可知,角域信息熵5种表征参数对柱塞泵滑靴外边缘偏磨磨损故障均具有一定的敏感性,均可作为滑靴磨损故障程度的评估指标。
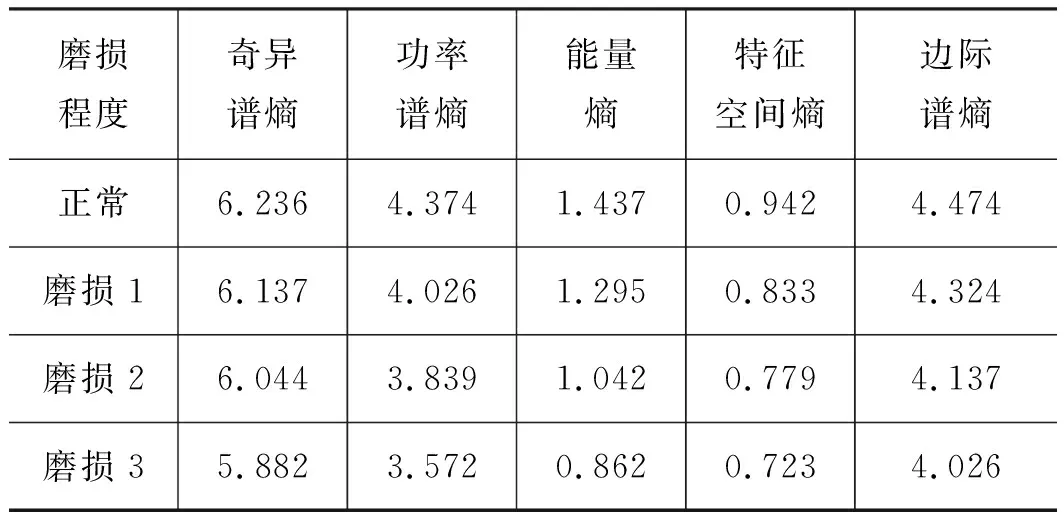
表1 角域信息熵平均特征值Tab.1 Angular entropy characteristic mean value
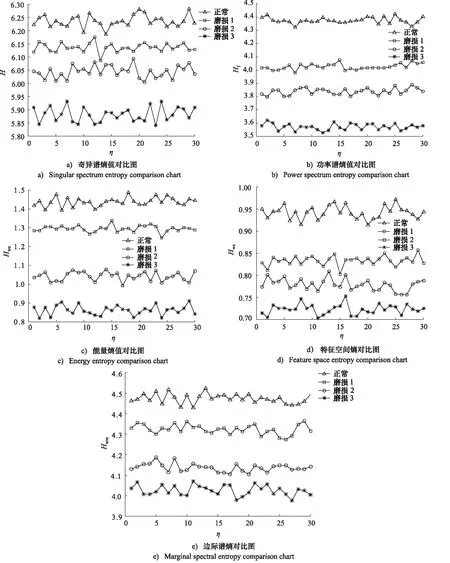
图10 角域信息熵特征值分布Fig.10 Charactersic value distribution of energy entropy in angular domain
5.2 状态评估模型的构建
将基于BP神经网络的基本概率分配识别定为4种模式,分别为:正常(A1)、磨损1(A2)、磨损2(A3)、磨损3(A4)。奇异谱熵、功率谱熵、能量熵、特征空间熵、边际谱熵的特征向量集都有4个特征向量,故隐藏层神经元数目h可取10,从而构造BP神经网络结构。运用逐层训练算法对训练样本网络参数初始化,信号正向传播,获得每层的连接权值和偏置。取损失函数为式(22)确定训练误差,误差反向传播,依次调节每层的权值和偏置,当损失函数值小于收敛阈值0.01时网络停止迭代。
(22)
式中,dk—— 实际输出
yk—— 理想输出
通过预设训练样本的方式进行概率分配,每种模式截取2000组信息作为训练样本,输入BP神经网络结构中进行5种特征向量的基本概率分配,计算公式为式(23),其结果见表2~表6。
(23)
式中,r—— 输出层节点
Ai—— 待评估故障模式
y(Ai) —— BP神经网络输出结果
由表2~表6看出,5种信息熵特征值都能较好表达故障程度,其中奇异谱熵、功率谱熵和边际谱熵对故障程度的区分效果明显,而能量熵和特征空间熵对故障程度的区分效果稍差,但依然能区分出滑靴磨损故障程度。采用基于D-S证据理论的角域多信息熵特征决策层融合算法,D-S证据理论的合成规则为式(24),融合后的可信度分配为式(25)。将表2~表6的基本概率分配信息进行组合,构建出能够对滑靴外边缘偏磨磨损程度进行有效区分的状态评估指标体系。
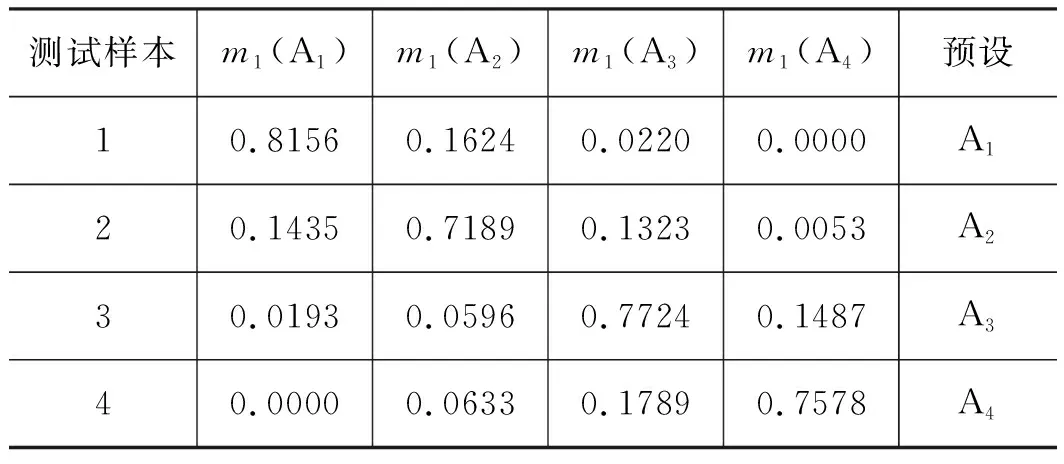
表2 奇异谱熵特征值的基本概率分配Tab.2 Basic probability distribution of singular spectraentropy eigenvalues
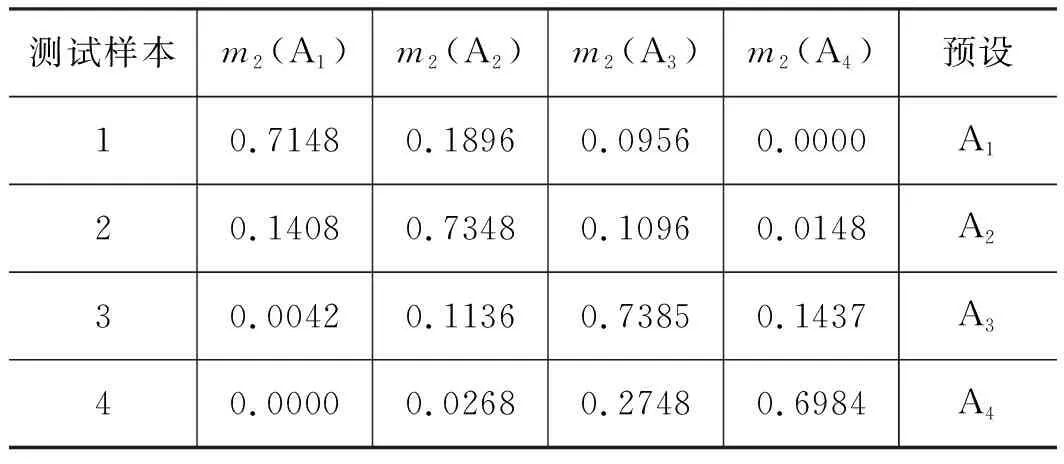
表3 功率谱熵特征值的基本概率分配Tab.3 Basic probability distribution of power spectrum entropy eigenvalues
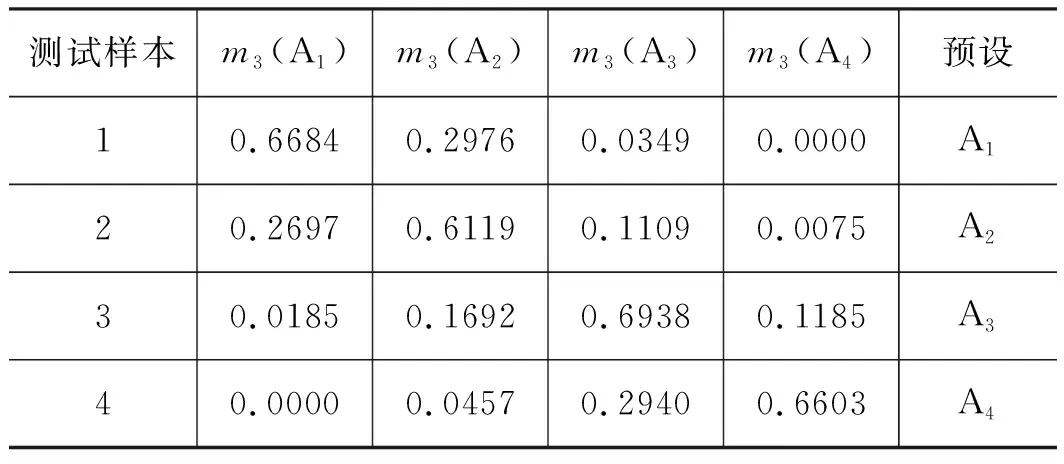
表4 能量熵特征值的基本概率分配Tab.4 Basic probability distribution of energy entropy eigenvalues
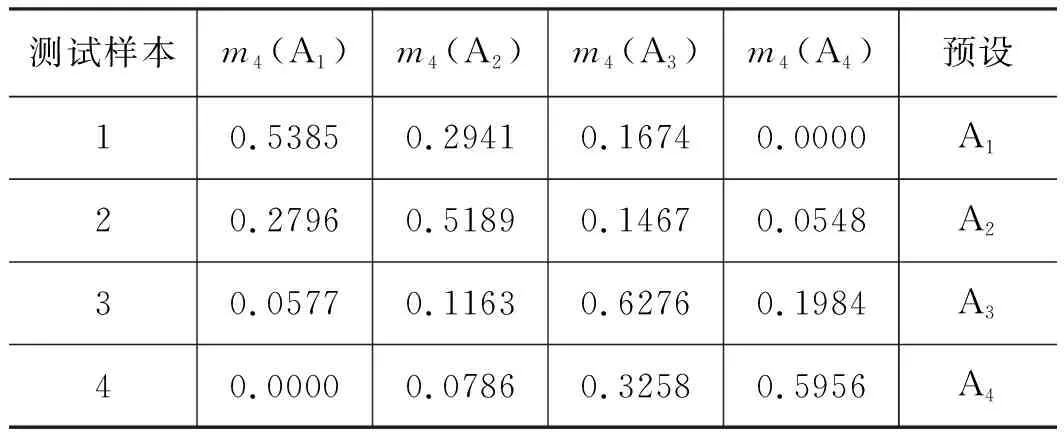
表5 特征空间熵特征值的基本概率分配Tab.5 Basic probability distribution of eigenvalue of eigenspace entropy
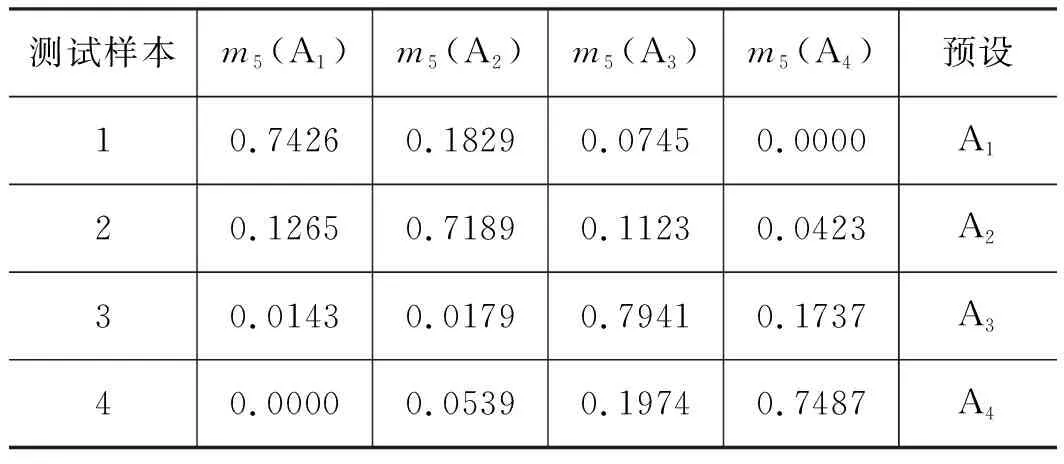
表6 边际谱熵特征值的基本概率分配Tab.6 Basic probability distribution of marginal spectrum entropy eigenvalues

(24)
式中,Mi—— 2Ω上的概率分配函数
Ω —— 样本空间
(25)
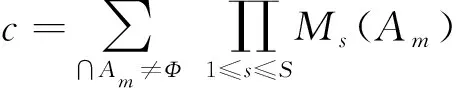
5.3 状态评估结果分析
滑靴4种工作模式截取800组数据作为测试样本,测试样本数据信息与训练样本信息保持一致,输入模型中进行状态评估测试试验,得出评估结果,如表7所示。
从表7可以看出,对应失稳阶段的磨损1模式状态评估准确率最高,其值为95.75%;正常阶段模式的状态评估准确率也高达94.45%;对应失效阶段的磨损2和磨损3模式状态评估准确率相对较低,分别为92.72%和91.45%。依据滑靴磨损机理,随磨损量的增加滑靴密封带将变窄,油膜厚度变薄,磨损率将显著增加。由于失效阶段模拟的这2种模式磨损程度均较大,从而导致角域信息熵特征值对这2种状态的区分能力变弱。

表7 状态评估结果Tab.7 Information entropy fusion evaluation results
从以上评估结果来看,本研究提出的角域多信息熵融合状态评估模型,可以实现在变转速工况下对柱塞泵滑靴外边缘偏磨磨损故障状态进行有效评估,且评估准确率较高,平均可达93.5%以上。
6 结论
(1) 本研究提出“角域信息熵”新概念,给出角域信息熵表征参数的提取方法,在柱塞泵变转速工况条件下对滑靴外边缘偏磨磨损故障振动信号进行5种表征参数的特征提取及表征参数对磨损程度的敏感性分析,证实磨损程度越大表征参数特征值越小,反映出的故障特征信息量越大,越容易确定故障程度,证实了5种表征参数提取的有效性。
(2) 本研究提出一种适合柱塞泵变转速工况的角域多信息熵融合状态评估新方法,通过提取5种角域信息熵表征参数建立滑靴外边缘偏磨磨损故障状态评估指标体系,结合BP神经网络基本概率分配算法和D-S 证据理论的决策融合算法构建出柱塞泵滑靴磨损状态评估模型。
(3) 设计了滑靴外边缘偏磨磨损故障模拟试验,采集了柱塞泵变转速工况下滑靴磨损故障振动信号,通过状态评估测试试验,验证了所提出状态评估模型和求解方法的有效性,且获得了较高的评估准确率。本研究可为EHA柱塞泵其他关键 摩擦副的状态评估方法研究提供参考依据,为建立EHA柱塞泵健康状态评估系统奠定理论基础。

