Application of Computational Methods for Hydrodynamic Pressure Caused by Supercritical Ship in Shallow,Finite or Deep-depth Waters

,-,-,-

(1.Department of Basic Courses,Naval University of Engineering,Wuhan 430033,China;2.Changjiang Institute of Survey,Planning,Design and Research,Wuhan 430010,China)

Abstract: The navigation safety, ocean or coastal engineering stability due to the waves and hydrody⁃namic pressure generated by a supercritical ship have received considerable attention. Because of the different hydrodynamic characteristics in different water depths, there are also differences among the computational methods.Computer programs implementing three computational methods for ship hydro⁃dynamic pressure in shallow, finite or deep-depth waters are developed and tested, such as analytical method, finite difference method and boundary element method. Meanwhile, Computational Fluid Dy⁃namics (CFD) method is also used to calculate the hydrodynamic pressure caused by a supercritical ship. Finally, by combining the computer programs implementing three computational methods with CFD method, the characteristics of hydrodynamic pressure caused by a supercritical ship in shallow,finite or deep-depth waters can be obtained accurately and analyzed systematically,which can provide a more systematic and comprehensive understanding for the engineers and researchers to choose the most appropriate method for related research.

Key words:CFD;supercritical ship;hydrodynamic pressure;finite difference method;shallow water;finite-depth water

0 Introduction

With the development and application of such fast types of ships as fast ferries, sealift naval ships, warships and so on, their role in the future will continue to grow. When a ship sails fast in seas, a canal, or a channel, if its depth Froude numberFh＞1 (Fh=V/gh, whereVis the ship speed,his the water depth,andgis the gravitational acceleration.),it is named a supercritical ship,the waves produced on the free surface and the hydrodynamic pressure fluctuations produced in the water will have a greater influence on ocean or coastal engineering, especially, in shallow water or coastal domain[1]. Moreover, compared with subcritical ships, the supercritical ships’high-speed characteristic makes them popular, and thus the interest for ocean and coastal applications is pro⁃gressively rising, and there are also potentials for military application. For example, the hydrody⁃namic pressure caused by supercritical ships can be better used for coastal defense of a country,such as warship detection, and pressure mine[2-4]. Thus, the studies of the hydrodynamic pressure field caused by supercritical ships will play a more significant role in the future.In this study,focus⁃ing on the computational methods’research of bottom hydrodynamic pressure field caused by su⁃percritical ships in different water depths,and analyzing the strengths and limitations of these com⁃putational methods will help researchers and engineers to choose the most appropriate method for calculation and analysis for different water depths.

Over the past several decades, numerous investigations have been done on the hydrodynamic studies of subcritical ships.On the basis of the linear potential flow theory,Tuck et al[5-8]used slen⁃der ship theory to calculate the waves and bottom hydrodynamic pressure of subcritical ships in shallow water. Gourlay[9-12]applied mathematical and computational techniques to predict the ship squat in several types of shallow water. Deng et al[13-15]obtained the hydrodynamic pressure charac⁃teristics caused by a subcritical ship in shallow water. On the basis of nonlinear theory and finite difference method,Jiang[16-17],Chen[18-20]and Huang et al[21]calculated the ship waves and wave resis⁃tance of subcritical and supercritical speeds in shallow water. Deng et al[22]further applied these mathematical and computational techniques to obtain the hydrodynamic pressure caused by super⁃critical ships in shallow water. On the basis of linear potential flow theory and boundary element method, He et al[23-24]calculated the ship waves in finite-depth water. Tezdogan[25]and Terziev et al[26]used CFD method to predict the squat and resistance of ship in restricted water. In addition to these methods, Tafuni et al[27]used smoothed particle hydrodynamics to study the bottom pressure generated by a boat in shallow water. Ma et al[28-29]developed nonlinear corrections of linear poten⁃tial-flow theory to calculate the sinkage and trim caused by a ship sailing at low speed in finitedepth water. Evidently, most of the above studies focused on the ship waves, sinkage or resistance,which belong to the near field of hull.However,studies on the bottom hydrodynamic pressure field,which belongs to the far field of hull, are limited. Notably, the studies on the bottom hydrodynamic pressure field are not only useful for coastal and ocean engineering, but also have great importance in military field, Bielański[2-4]used boundary element method for determining the pressure signa⁃tures caused by a merchant ship and a motorboat sailing at low speed in different water depths.

Computer programs implementing three computational methods for ship hydrodynamic pres⁃sure in shallow,finite or deep-depth waters are developed and tested,such as analytical method,fi⁃nite difference method and boundary element method. The three computational methods have been presented in our previous literatures[13-15,22], so this paper mainly focuses on the fourth CFD method and the application of computational programs implementing three computational methods.Accord⁃ing to the computational programs and CFD method for ship hydrodynamic pressure,the advantages and limitations of each method are presented, and the characteristics of bottom hydrodynamic pres⁃sure caused by supercritical ships can be obtained and analyzed systematically.

1 Computational case

As shown in Fig.1, the water width isw, and its depth ish; when a supercritical ship sails along the water center-line,a Cartesian coordinate system is moving with the ship,its originOis lo⁃cated at the hull center,itsx-axis points to the ship bow,itsy-axis points to the sidewall,andz-ax⁃is is vertically upward.

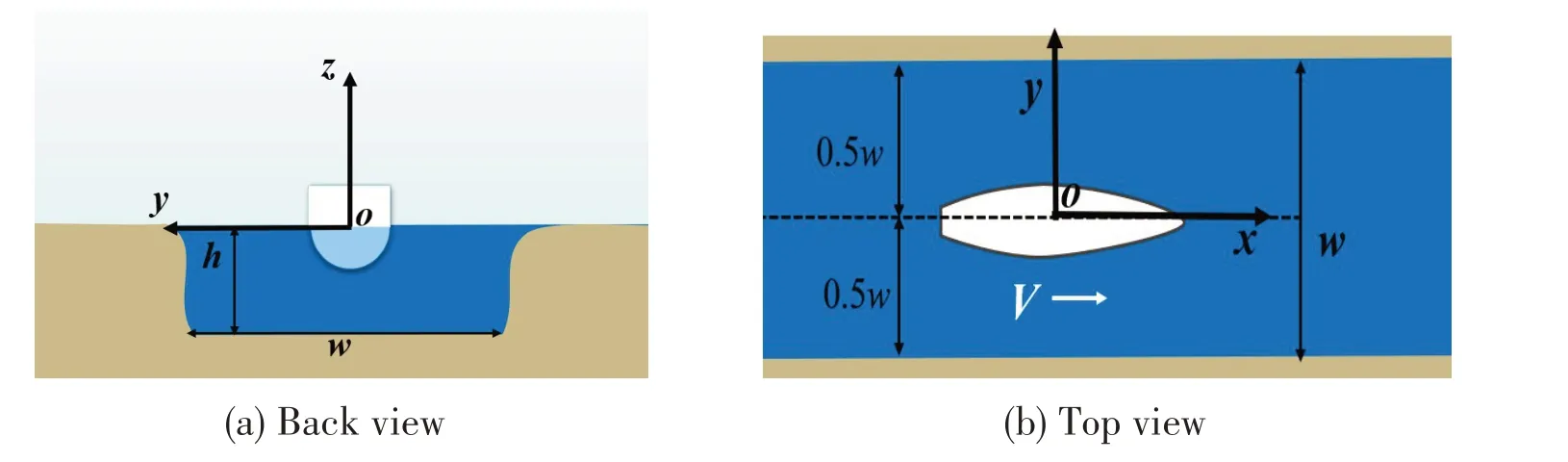
Fig.1 Cartesian coordinate system

Based on analysis of the experimental re⁃sults[30-31],the hydrodynamic pressure character⁃istics of supercritical ship in different water depths are different, thus, their corresponding computational methods may also be different.The Wigley and experimental ships are used for the computational methods’research, namely, analytical method, finite difference method,boundary element method and CFD method. These two ships’main dimensions are the same, as shown in Tab.1,and the Wigley hull is expressed as:

Tab.1 Main parameters of the Wigley and experimental ship models

whereLis the ship length,Bis width,anddis draft.

However, because of the main difference of two ships’stern shapes, as shown in Fig.2, for ef⁃fective research, an increase in the length of Wigley hull by 0.1 times at stern represents the stern effect of experimental hull[13].

Fig.2 Wigley and experimental ship models

2 Computational programs

2.1 Analytical method

Supposing that the fluid is incompressible and inviscid, the flow satisfies Euler equation and the mass conservation equation are

The integral functionQof open water is shown in Fig.3, which shows an attenuation func⁃tion with increasingk. However, the integral func⁃tionQof restricted water has strong singularity,which is difficult to solve analytically, and the fi⁃nite truncation method can be used for integration whenk→+∞，MATLAB is used for program⁃ming. Nevertheless, on the basis of the previous analysis[13], forw＞3.0L, the sidewall boundary has a slight influence on the hydrodynamic pres⁃sure, so the water ofw＞3.0Lcan be regarded as open water, and the hydrodynamic problem can be solved by using the integral functionQof open water.

2.2 Finite difference method

For some supercritical speeds in shallow water,such as a supercritical ship sailing at near critical speed,the first term of Eq.(4)is not large compared with its third term,so its third term should be considered,then the finite difference method can be used to solve nonlinear Eq.(4).

The rectangular computational domain chosen for calculations has an upstream boundary of 4Lfrom the bow, a downstream boundary of 4Lfrom the stern, a sidewall boundary of 1L-2.25Lfrom the plane of symmetry,and a bottom boundary of 0.1L-0.5Lfrom the keel.Then,this computational domain can be divided into a uniform square mesh.For most supercritical speeds,the mesh spacing in thex-andy-directions is Δx= 0.05Land Δy= 0.05L,which can meet a high-precision,that is,for the case of the water ofw=4.5L, there are 14 400 grids in one plane of the computational do⁃main. However, the closer the speed to the critical one, the harder it is to converge, making the grids alongy-direction denser, capable of meeting a high-precision result, that is, Δyis less than Δx.of the central difference scheme,thex-direction is marked withiwhiley-direction is marked withj.

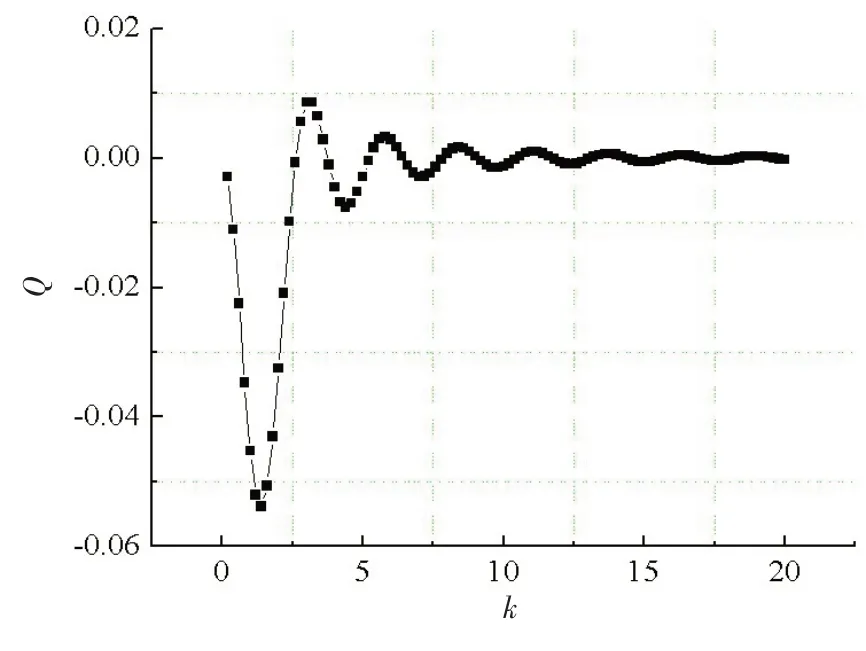
Fig.3 Curve of integral function Q changing with k

Therefore,nonlinear Eq.(4)is discretized as:

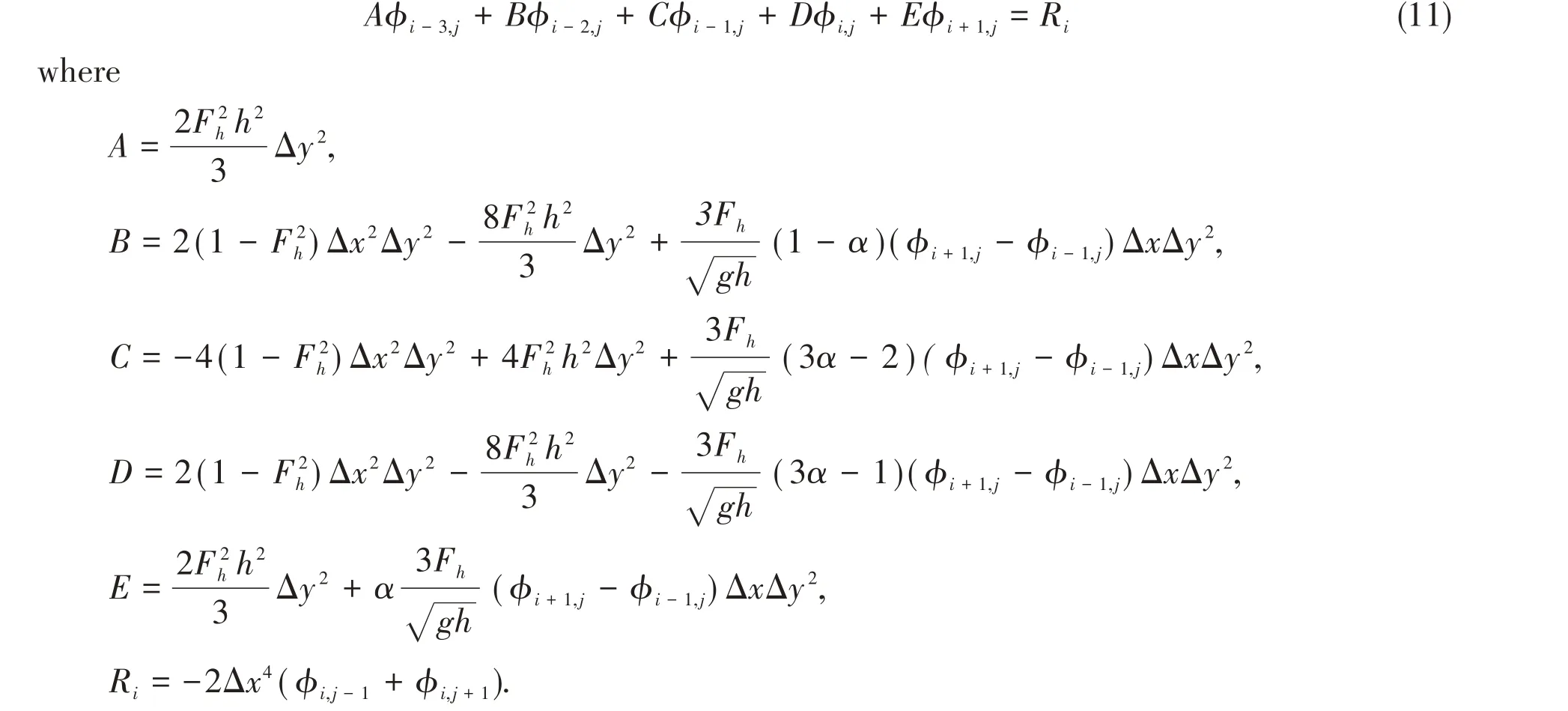
The boundary conditions are the same as those in Eq.(6)to Eq.(8),which can be discretized in⁃to the difference equations on every mesh point. Then, combining with Eq.(11),φcan be solved,andCpcan be obtained.

2.3 Boundary element method

When the water depth is not shallow,but finite,the flow parameters do not satisfy the shallowwater assumption,then the boundary element method can be used.Based on the potential flow theo⁃ry,by using the velocity potentialΦ,Eq.(3)can be simplified,

Furthermore, based on Eq.(13) and Eq.(14) by using the source image method to represent the free surface and bottom effects,then,Eq.(15)forG,which represents the superposition of the source and its numerous mirror images of the free surface and bottom,can be obtained,

Eq.(16) consists of double integral and single integral, and it has the characteristics of singu⁃larity, oscillation and infinite limit, how can this equation be solved? Firstly, the double integral of Eq.(16)can be simplified to single integral by Laguerre and exponential integral methods,and then,the singularity and infinite limit of single integral can be solved by residual truncation method.Meanwhile,the singularity and oscillation of partial derivation in Eq.(16)can be eliminated by Rom⁃berg integral method,which can meet a super-linear automatic convergence[33].

2.4 CFD method

With the development of computational fluid dynamics, a CFD solver can be used to calculate the ship hydrodynamic pressure,such as STAR-CCM+.The physics models chosen for calculations are viscid, three-dimensional, implicit unsteady flow, and Euler multi-component liquid, then, by using thek-ωSST turbulence model, the continuity equations and Reynolds-averaged Navier-Stokes equations are solved by the finite volume method while the free surface is captured by the VOF method[34].

The computational domain is the same as that of the finite difference method, and has a top boundary of 0.5Lfrom the free surface. Furthermore, the inlet and outlet conditions are the velocity inlet and pressure outlet, respectively; meanwhile, the unsteady method requires a downstream damping zone to prevent wave reflection from it.

For the mesh generation, it is necessary to ensure that there are more than 80 grids per unit wave length, meanwhile, there is sufficient mesh density around the boundaries. For the above pur⁃poses, by increasing the number of grids in a certain proportion, a large number of numerical re⁃searches on mesh convergence were carried out[35]. Finally, six sets of meshes with base sizes of 0.1L, 0.075L, 0.058L, 0.05L, 0.042Land 0.0375Lwere selected for calculation and comparison to show the mesh influence on the calculation results, as shown in Tab.2. It can be seen that, with the mesh size decreased, the number of grids increases by about 200 000, 400 000 and 600 000, and the number of cells of Mesh F is about 2.5 million more than that of Mesh A. With the applications of trimmed mesher and prism layer mesher,the number of prism layers we choose is 2,its thickness is 0.000 83L,thus,there are sufficient grids around boundaries,such as,the free surface,the ship sur⁃face,and so on.Then,the computational domain is divided into an unstructured mesh.

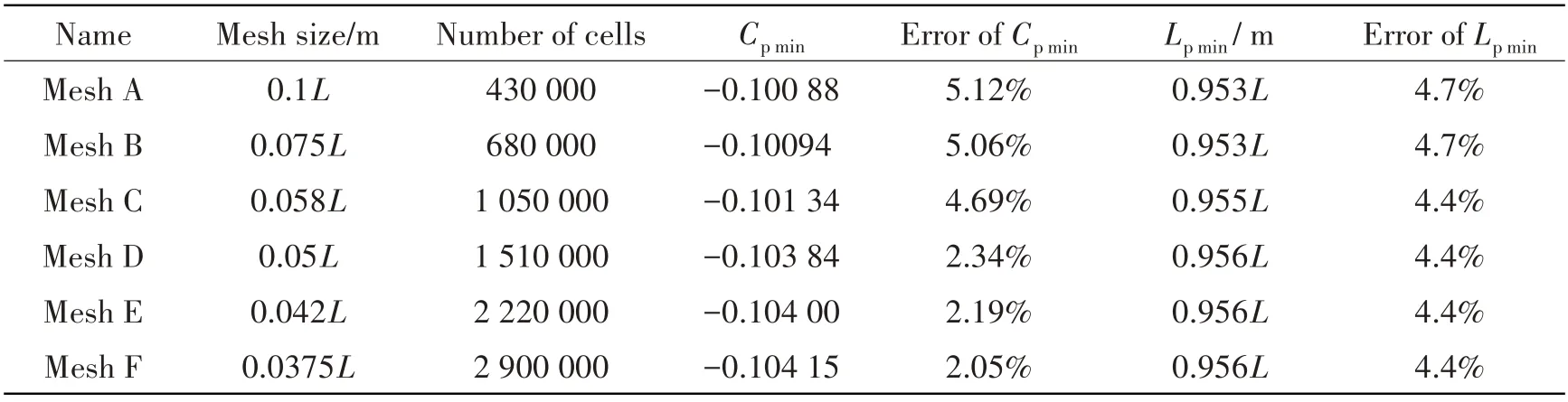
Tab.2 Mesh convergence analysis(h=0.1L,Fh=1.56)

For the selection of time step,an implicit unsteady solver is used to model time marching.The selection of time step is mainly dependent on the ship length and its speed,thus,Δt= 0.01L/Vis se⁃lected for the time step, and the second-order temporal discretization scheme is used[35]. Mean⁃while,the convergence time is mainly dependent on ship speed and computational domain,general⁃ly,for a supercritical ship sailing in waters ofw＞3.0L,the simulation meets the convergence crite⁃ria by running for 900Δt, that is, the iterative residual is lower than a given value, some forces act⁃ing on the hull, such as longitudinal and vertical hydrodynamic forces, are stable, and the pressure field around ship does not change significantly.However,for a supercritical ship sailing in narrower channel,the simulation needs to run longer for convergence,because of the boundary reflection.

For the water ofw=4.5Landh=0.1L, the bottom hydrodynamic pressure field caused by a su⁃percritical ship sailing atFh=1.56 is calculated on the basis of the six sets of meshes.The longitudi⁃nal pressure curves of the transverse distancey=0.5Lare shown in Fig.4, and the calculatedCpminandLpminare shown in Tab.2,Cpminis the negative pressure peak, andLpminis the distance from the midship(x/L= 0)to theCpminposition,they are both important characteristic parameters in the stud⁃ies of hydrodynamic pressure. For the water ofw=4.5Landh=0.2L, the bottom hydrodynamic pres⁃sure caused by a supercritical ship sailing atFh=1.38 is calculated based on Mesh A and Mesh D.The comparisons of the bottom hydrodynamic pressure contours are shown in Fig.5.When the mesh is denser, Tab.2 shows that the error ofCpminbecomes smaller while Fig.4 and Fig.5 show that the characteristics of the bottom pressure of different meshes are approximately the same. Thus, the mesh independence can be satisfied,we choose Mesh D for calculations,the corresponding mesh di⁃visions are shown in Fig.6.

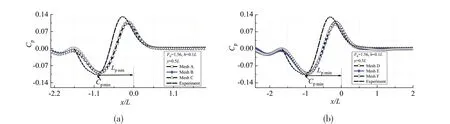
Fig.4 Comparison of longitudinal pressure curves based on different meshes(w=4.5L)

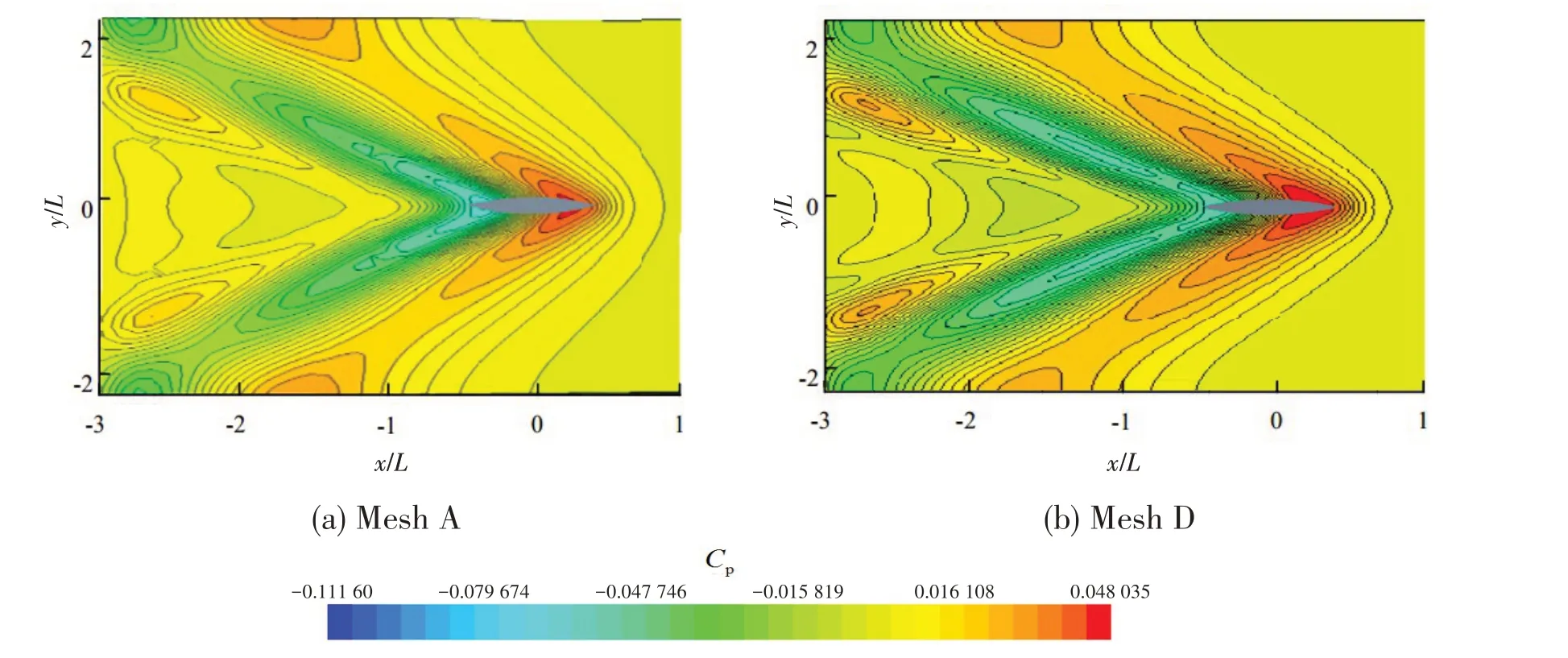
Fig.5 Comparison of the bottom hydrodynamic pressure contours(w=4.5L,h=0.2L,Fh=1.38)

Fig.6 Mesh D(w=4.5L,h=0.1L,y ≥0)

3 Results and discussion

For different Froude numbers of a certain depth, analytical method (Method A), finite differ⁃ence method (Method B), boundary element method (Method C) and CFD method (Method D) are used to calculate the ship hydrodynamic pressure in shallow, finite or deep-depth waters.,then, the calculated results are compared with the experimental results. Thus, the advantages and precision of each method under different water depths are shown, which is important to give the discrimina⁃tive codes such as ship speed, water depth and width, and useful for programming high-precision computer programs.However,due to the larger-depth water,the existing ship cannot reach a higher Froude number,so the relevant experiments cannot be carried out,the results’comparisons of high⁃er Froude number are not shown.

Furthermore, the computer programs with three computational methods are used to calculate the ship bottom hydrodynamic pressure in shallow, finite or deep-depth waters. As shown in Fig.7,according to the discriminative codes for input parameters such as speed, water depth and width, a certain computational method is automatically called and run, and then, the output calculated re⁃sults, such as pressure curve and negative pressure peak, will be verified by the experimental re⁃sults or the CFD method’s results, and the calculated precision is tested. Thus, the accurate analy⁃sis of ship hydrodynamic pressure field is carried out.

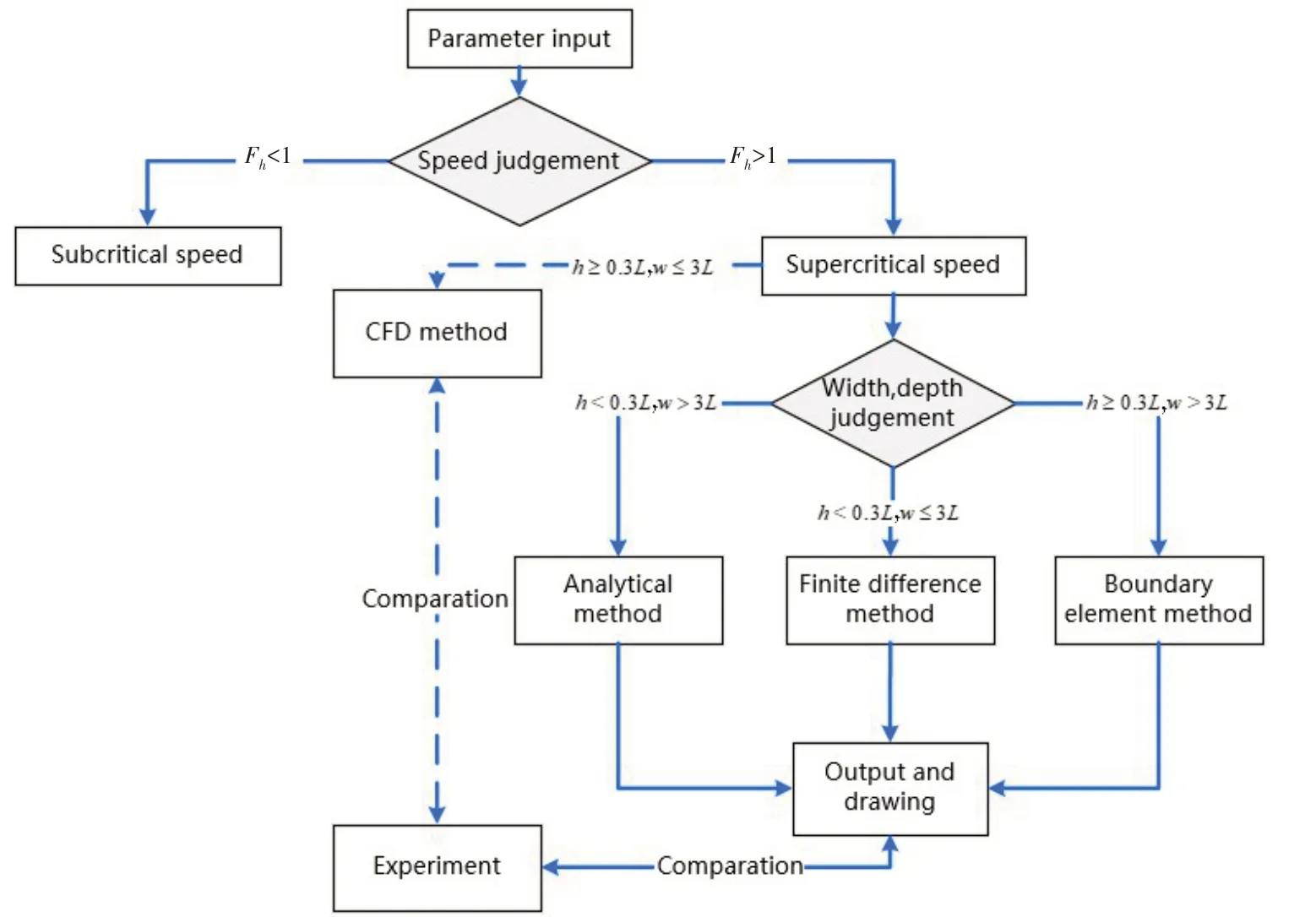
Fig.7 Computer programs implementing three computational methods

For different-depth waters ofw=4.5Lorw=2.0L, the comparisons of the longitudinal pressure curves andCpmincalculated by these computational methods are shown in Fig.8 to Fig.16, the bot⁃tom hydrodynamic pressure characteristics change with the water depth and the Froude number can be analyzed, and the advantages and limitations of each method in different-depth waters can be shown.

(1)For shallow water

For shallow water ofh= 0.1Landh= 0.2L, when the water widthw= 4.5L, the sidewall ef⁃fect is very weak, Fig.8 and Fig.9 show thatCpmincalculated by Methods A and B are closer to the experimental one at most supercritical speeds,because Methods A and B are based on shallow-wa⁃ter equation.

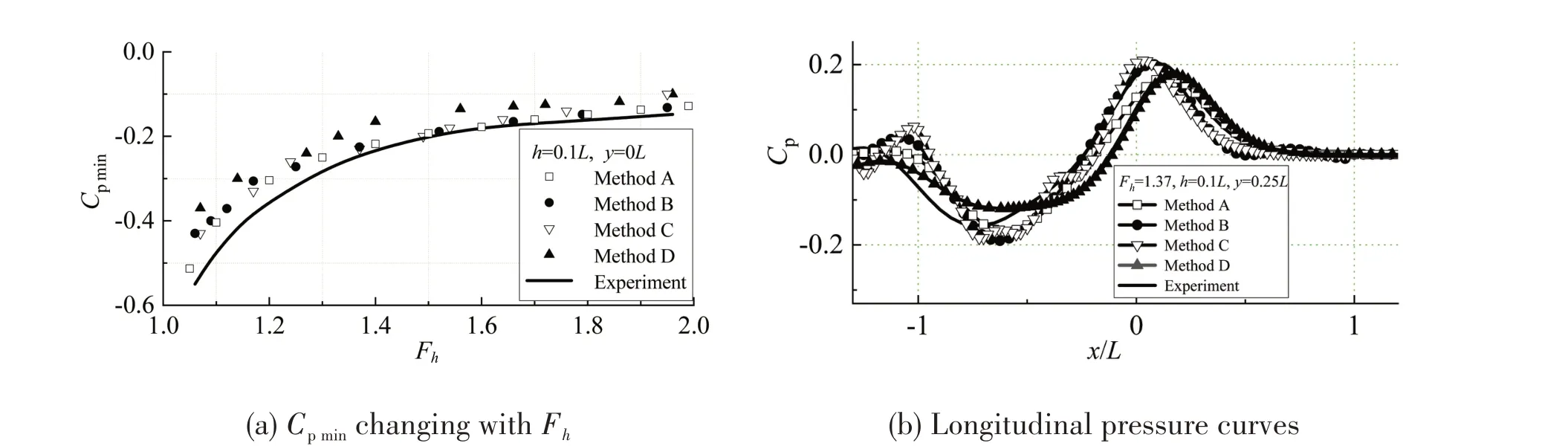
Fig.8 Comparisons of results of computational methods with h=0.1L

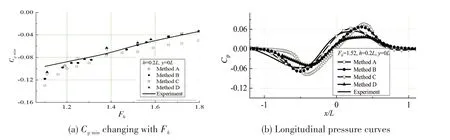
Fig.9 Comparisons of results of computational methods with h=0.2L

Therefore,Methods A or B can be used to obtain the ship hydrodynamic pressure field of shal⁃low water, and the calculated results ofh= 0.1Landh= 0.2Lare shown in Fig.10 and Fig.11. By comparing Fig.10(a) and (b), and comparing Fig.11(a) and (b), it can be seen that the results of dif⁃ferent transverse distances are in good agreement with the experimental ones,and the backward po⁃sition of the negative pressure peak is more backward with the increase of speed.

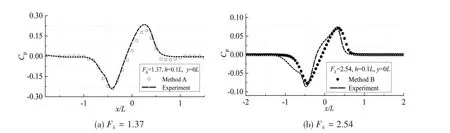
Fig.10 Comparison of longitudinal pressure curves(h=0.1L)

Fig.11 Comparison of longitudinal pressure curves(h=0.2L)

However, for the shallower water ofh= 0.1L, as the Froude number gets closer to the critical speed,the dispersion effect,nonlinear effect and time-varying effect are more obvious,then the dif⁃ference between the calculated results and experimental results becomes more obvious. Thus, fur⁃ther researches near the critical speed are needed in the future.

The water width ofw＜3.0Lis of restricted water, wave interactions will occur between the ship and sidewall boundary, and impose significant nonlinear effects on the bottom hydrodynamic pressure field. Because of the reflection effect between the ship and sidewall boundary, when writ⁃ing the computer programs,the discriminative codes are given to determine whether the water width is less than 3.0L. Ifw＜3.0L, the computer gives the instruction to call the finite difference method(Method B)to run.And then,the calculated result of Method B is compared with the results of CFD method(Method D),as shown in Fig.12,which represents that there are two negative pressure peaks in the distance fromx/L=-4.0Ltox/L= 0Lin the water ofw=2.0L, while there is only one negative pressure peak in the same distance in the water ofw=4.5L.

Furthermore, Fig.12 shows that the longitudinal pressure curves andCpminofw=4.5Lobtained by two methods and experiment are approximately similar,and the longitudinal pressure curves andCpminofw=2.0Lcalculated by Method B are approximately the same with those by Method D, which shows that Method B can accurately calculate the pressure reflection of the sidewall boundary.

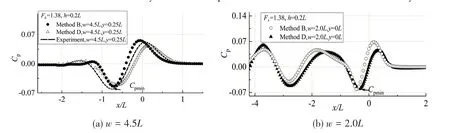
Fig.12 Comparison of longitudinal pressure curves(w=2.0L and 4.5L)

(2)For finite or deep-depth waters

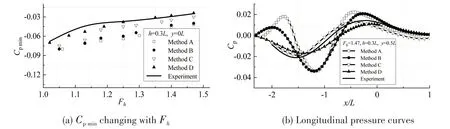
Fig.13 Comparison of the results of computational methods(h=0.3L)

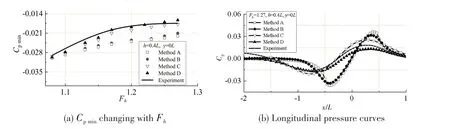
Fig.14 Comparison of the results of computational methods(h=0.4L)

As shown in Fig.13 and Fig.14,for the water depthh= 0.3Landh= 0.4L,the flow parameters do not satisfy the shallow-water assumption,the water is of finite-depth.Fig.13 and Fig.14 indicate that the longitudinal pressure curves andCpmincalculated by Methods C and D are more consistent with the experimental ones than those calculated by Methods A and B, because Methods C and D do not average the perturbation velocity potential along the water depth,and do not use the shallowwater assumption.Therefore,for finite-depth water,Method C is chosen to calculate the ship hydro⁃dynamic pressure field and compare the results,as shown in Fig.7.

Take the water ofh= 0.3Lfor instance,using the computer programs to calculate.As shown in Fig.7, ifh= 0.3Landw= 4.5L, the boundary element method (Method C) can be used. And then,the calculated result of Method C is compared with the experimental result, as shown in Fig.15,which shows that the calculated results are very close to the experimental ones, and the results of different transverse distances are in good agreement with the experimental ones. Certainly, for the deeper water, the bottom boundary is much farther from the hull, Method C can also be chosen for calculations,which may achieve accurate results.

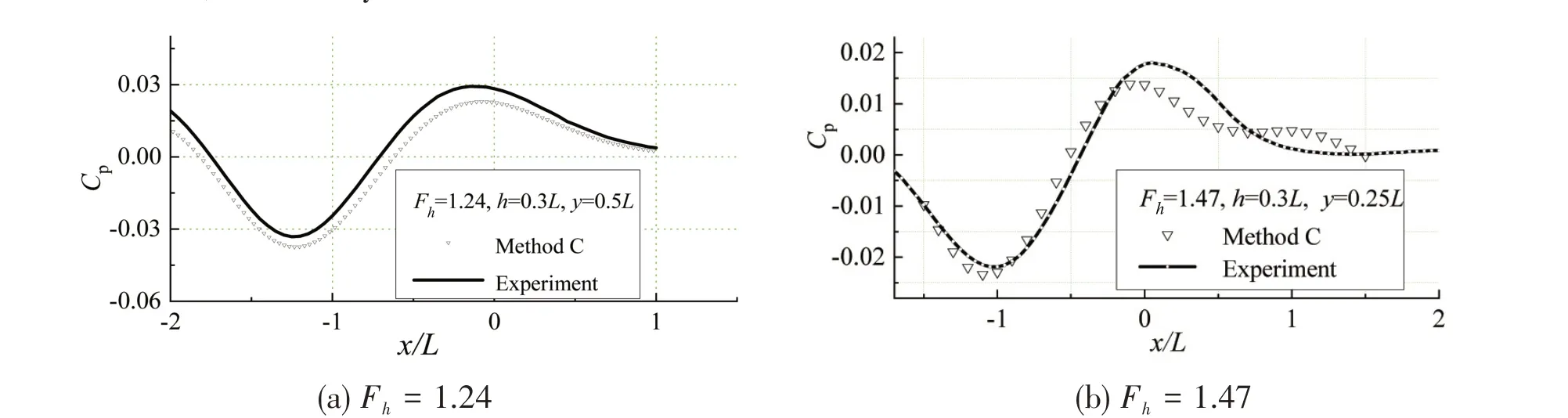
Fig.15 Comparison of longitudinal pressure curves(h=0.3L)

According to Figs.8-15, the results calculated by CFD method are more likely to be of highprecision.When the water is deeper,as shown in Fig.16,the results calculated by CFD method are also in good agreement with the experiment.

Fig.16 Comparison of longitudinal pressure curves(h=0.4L and 0.5L)

However, based on a great number of researches and calculations for CFD method, it is con⁃firmed that the shallower the water,the denser the boundary mesh needs to be,and the hull degrees of freedom need to be considered. This may be the reason why CFD method’s precision is not high enough forh=0.1L.Thus,the further research for the shallower water is needed.

4 Conclusions

The computational methods of the bottom hydrodynamic pressure field caused by supercritical ships from shallow to finite-depth water,and from open to restricted water are investigated.By com⁃parison, the advantages and limitations of each method are shown and analyzed, and the computer programs implementing three computational methods with high-precision are developed and tested for calculating the ship bottom hydrodynamic pressure in shallow,finite or deep-depth waters.

Then, by combining the computer programs with CFD method, the hydrodynamics pressure caused by supercritical ships in shallow, finite-depth, deep, open and restricted waters can all be obtained and analyzed. It can be seen that| |Cpmindecreases with the increase ofFhfor the sameh,which means the higher the Froude number , the smaller the bottom hydrodynamic pressure coeffi⁃cient generated by ship.| |Cpmindecreases with the increase ofhfor the sameFh, which means the deeper the water, the smaller the bottom hydrodynamic pressure coefficient generated by ship.Meanwhile, whether it is shallow water or finite-depth water, theCpminposition is no longer below the midship, but near below the stern, which is quite different from that of a subcritical ship[13], be⁃cause of the dispersive effect.

Meanwhile, the computer programs combined with CFD method can give a more systematic and comprehensive presentation to researchers and engineers, and can help them to choose the most appropriate method for studying supercritical ships in waters with different depths. Further⁃more, these computational methods are helpful for the studies of the more complex waters, and can also be expanded to calculate ship wave,sinkage,trim,resistance and so on.