悬索桥的动力特性及爆炸荷载下的动力响应分析
王 雅
(山西路桥集团试验检测中心有限公司 太原市 030000)
桥梁是城市重要的交通枢纽,爆炸将对桥梁的结构安全产生严重影响。为此,以山西某在建自锚式悬索桥为例,运用ANSYS有限元分析软件,对其在爆炸冲击波下的动力响应进行研究,并分析了爆炸参数对冲击波荷载作用的影响。
1 工程概况
该桥为建在城市主干路的三塔双索面自锚式悬索桥,该桥的跨径布置为50+80+168+168+80+50=596m,采用组合梁和混凝土梁的混合主梁形式,中跨、边跨465.6m范围内为钢-混凝土组合梁,桥宽50.5m,吊索间距为6.4m。混凝土主梁和主塔均为C50混凝土材料,钢梁为Q345钢,主缆和吊索材料均为镀锌平行钢丝。
2 模型建立
为贴合实际工程情况,笔者运用ANSYS分析软件建立实体模型,根据材料及模型的复杂程度,主梁选用Solid185和Solid186单元模拟建立;因主塔为变截面不规则混凝土实心结构,采用Solid186单元划分网格才可实现,采用LINK180单元模拟主缆和吊索,且将其设置为仅受拉,以反映其柔性特征。该桥截面形状多样,根据设计图纸,借助CAD作出不同截面形状,导入ANSYS中形成实体模型。截面模型如图1所示。

图1 全桥实体模型图
3 模型验证
桥梁的动力特性是其固有属性,是结构计算动力响应的基础[1]。通过自振特性模拟计算,得到该桥的前两阶频率和振型如表1和图2所示。

表1 前2阶动力特性
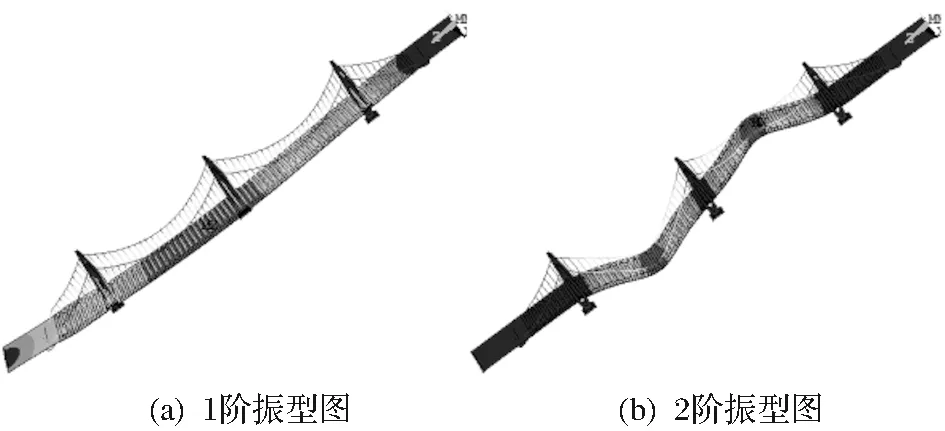
图2 前两阶振型图
张超等[2]考虑主塔刚度,通过Rayleigh法公式(1)来计算三塔自锚式悬索桥一阶反对称竖弯振动频率:
(1)
γ0是与边跨、主跨跨径相关的参数,按式(2)计算:
(2)
α为反对称竖弯振型的主塔刚度系数,按式(3)计算:
(3)
代入本桥相关参数可得,γ0=3.43×10-7m-4,α=8.5×10-7m-2,求得fv=1.0442Hz。
对比解析解和数值模拟解,两者偏差较小,仅为3.3%,说明数值模型建立正确,可依此模型进行爆炸冲击波下的动力响应分析。
4 动力响应分析
为研究爆炸对悬索桥的影响,因该桥为对称结构,将炸药爆心设置在全桥桥面对称中心上空15m高处,炸药量取800kg,计算对称爆炸荷载作用下结构的动力响应。
根据动量守恒,将爆炸荷载以初速度的形式施加在主梁节点,各节点初速度按式(4)表示。
(4)
其中,m为单位桥长质量(kg/m);v0为初速度(m/s);b为桥宽(m);ir为反射比冲量。
根据文献[3]可得式(5),其中,W是炸药量(kg);R是爆心与测点的距离(m)。
(5)
代入该桥单位桥长及桥宽,可得初速度计算公式如式(6):
(6)
考虑到计算时长,在ANSYS中设置分析时间t=200s,分析步设置为100步。通过数值模拟,得到下面4个时刻全桥的挠度变形云图如图3所示。
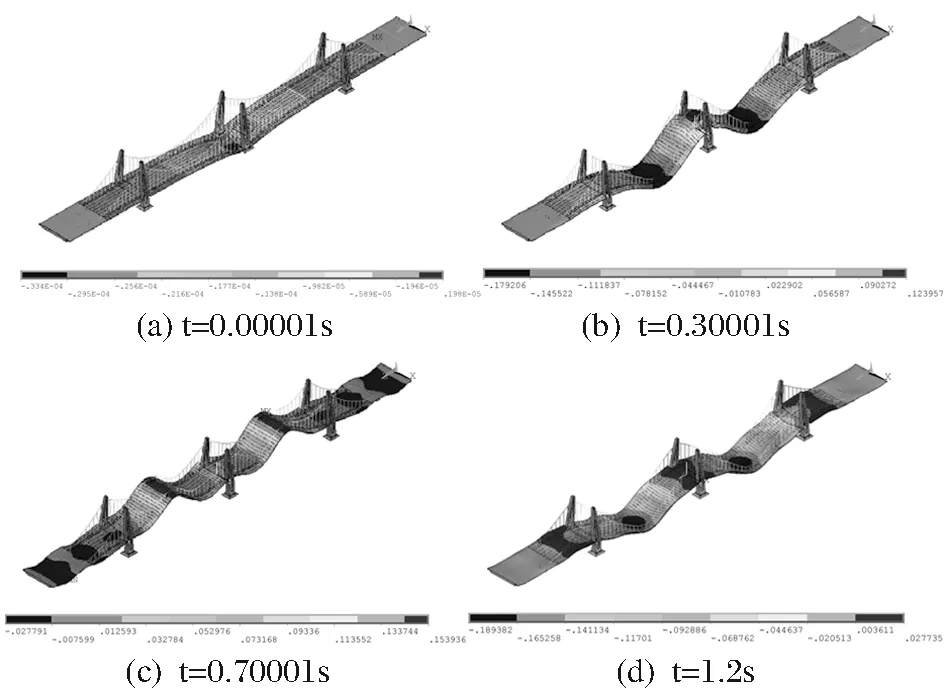
图3 部分时刻挠度变形云图
在对称荷载作用下,悬索桥经过1.2s左右从非稳态阶段(节点变形幅度大,衰减迅速)变为稳态阶段(在成桥状态平衡位置上下波动),变形由中心向两侧扩散,两侧锚固跨变形很小,在1.2s时第三跨跨中中心节点向下位移最大,为0.189m,由此可得此截面为最危险截面。此截面桥面中心节点位移时程曲线和弯矩时程曲线如图4、图5,在荷载作用初期,此节点内力和位移都急剧变化,正负弯矩及变形量接近稳态阶段的两倍。因反射波耦合作用,内力会存在突增现象,但整体仍为衰减趋势。

图4 第三跨跨中桥面中心节点位移时程曲线

图5 危险截面弯矩时程曲线图
在爆炸荷载作用初期,吊索轴力会存在无轴力状态,桥梁对称中心截面两侧的吊索轴力最大,最大值达到12.6MN,见图6;主缆最大拉力出现在此吊索两侧,最大拉力为82.9MN,见图7。

图6 桥梁对称中心两侧吊索轴力时程曲线

图7 主缆拉力最大处时程曲线图
5 爆炸荷载参数影响分析
(1)炸药量
目前精确制导常规炸药量为200~450kg,少数当量为800~1200kg[4]。炸药量不同时,爆炸威力不同,为探究此影响,模拟在爆炸高度为15m,炸药量分别为400kg、800kg、1000kg时该桥的动力响应。

表2 不同炸药量下各构件的内力与变形
爆炸高度一定,炸药量由400kg增加到1000kg时,主梁内力与变形最大值均有明显增加,吊索轴力最大值仍在全桥中心截面两侧吊索处,且轴力增幅高达74.9%,主缆拉力最大值增幅最小,仅为16.4%。
(2)爆炸高度
除炸药量以外,爆炸高度对冲击波荷载也有影响,为探究炸药在不同高度下该桥的动力响应,分别模拟了800kg炸药在全桥桥面中心正上方10m、15m、20m时各构件的内力与变形情况。

表3 不同爆炸高度下各构件的内力与变形
炸药量为800kg时,高度由10m增加到20m时,主梁内力和变形最大值均有明显减少,内力降幅为11.3%,吊索轴力降幅最大,高达26.6%,主缆变化幅度最小,减小了4.8%。
上述5种工况下,主梁最大内力均出现在第三跨跨中截面,最大变形也在此截面桥面中心节点处,进一步验证了对称爆炸荷载下最危险截面为第三跨跨中。炸药量和爆炸高度变化时,主梁和吊索变化较明显,主缆变化幅度最小,因为爆炸参数不同时,对主缆的线型和水平力影响微乎其微,所以其拉力没有大幅变化,但是附近的吊索会受到较大冲击波作用,影响显著。
(3)爆心在横桥向不同位置
考虑到实际可能发生的爆炸情况,将500kg炸药设置在近地面(距离桥面1m高度处),分析其爆心在该桥第三跨跨中截面桥面对称中心、右幅第2、第4车道中心桥面1m高处时爆炸下的动力响应,各构件内力与变形值对比如表4。
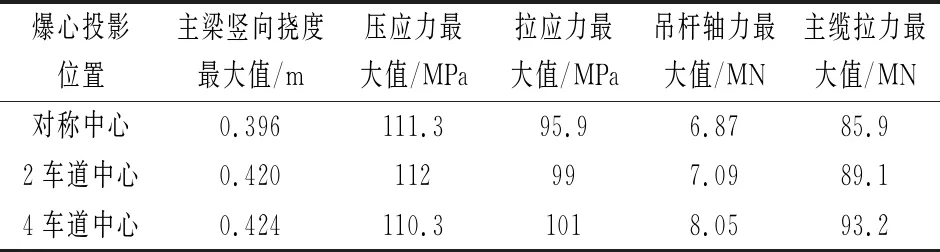
表4 爆心位置不同时各构件内力和变形最大值
由表4可见,在本文研究的工况下,沿横桥向随着爆心偏离桥梁中心轴线位置越远,除主梁最大压应力外,其余各构件的内力和变形最大值均有所增加。具体分析如下:由于爆炸高度和炸药当量相同,爆炸冲击波作用在爆心投影位置时的瞬时最大压应力基本不变;当爆心偏移桥梁中轴线,与缆索区的距离缩短,冲击波对爆心附近吊杆的作用显著增强,再结合弯扭耦合的作用,导致第三跨跨中两侧吊杆轴力和附近局部主梁位移最大值增加;上述三种工况下,主缆的线型和水平分力变化不明显,主缆拉力最大值的增幅不明显。
6 结语
以某座在建自锚式悬索桥为例,运用ANSYS软件分析其自振特性及其在爆炸冲击荷载下的动力响应,并分析爆炸参数及爆心位置对动力响应的影响。
(1)对比该悬索桥一阶反对称竖弯的数值解和解析解,两者偏差仅为3.3%,可得该数值模型的正确性。
(2)以800kg炸药为例,得到在对称爆炸冲击波下最危险截面为第三跨跨中,且各构件内力最大值均出现在非稳态阶段,故此阶段为该桥抗爆设计工作的重中之重。
(3)炸药量的增加与爆炸高度的减小,会使得主梁和吊索内力显著增加,但因对主缆线型和水平力影响较小,主缆内力变化不明显。
(4)500kg炸药在横桥向不同桥面位置近地面处爆炸时,随着与桥梁中心线距离的增加,除主梁最大压应力外,其余各构件的内力和变形最大值均有所增加。

