电驱动测井绞车电缆张力模糊控制方法研究

李炳林，杨双业，樊勇利，秦羿涵，夏 辉，王 议

(1. 西南石油大学 机电工程学院，成都610500；2. 宝鸡石油机械有限责任公司，陕西 宝鸡721002；3. 中油国家油气钻井装备工程技术研究中心，陕西 宝鸡721002)

电驱动测井车是油气田开采中的重要设备，电缆张力是测井仪器升降过程中最重要参数。恒张力控制可以使测井仪器稳定运行，防止电缆拉断等井下事故发生，确保测井数据准确率，提高测井作业效率[1-2]。例如，在水平井测井过程中，测井仪器和电缆固定在井下钻具上随着钻杆一起下放和上提，要求测井绞车提供合适的张力使得电缆始终处于张紧状态，避免电缆发生打卷破坏[3]。国内的电缆张力控制多数依靠绞车工的经验，通过观察显示器上参数进行手工操作，不断地修正电机转速来控制张力。这种控制方法属于无反馈和检测环节的开环控制，存在很大误差和不确定性，严重还可能出现误操作，导致安全事故的发生[4-5]。由于测井工况复杂，电缆在缠绕过程中绞车的半径还不断发生变化，电缆张力控制系统比较复杂，常规的PID控制方法参数单一性，易出现振荡，不能满足对电缆张力控制系统的实时调控要求，难以满足对张力控制的响应速度和控制精度要求，且存在不确定性[6-7]。本文以7 000 m电驱动测井车为对象，将模糊PID控制算法以PLC语言的形式写入了S7-1200 型PLC的CPU当中，张力计的张力信号传送给PLC进行自适应PID参数整定，控制电机的转速，实现电缆张力的自动控制。

1 测井绞车电缆张力控制系统的原理

智能化电驱动测井的恒张力绞车采用交流永磁同步电机驱动齿轮减速器及滚筒。永磁同步电机是1个多变量、强耦合的非线性系统，如果电机电流波动较大，恒张力控制的稳定性将大幅降低，电机电流闭环控制是恒张力控制的关键[8]。因此，电缆绞车高性能的张力控制系统采用双闭环控制方式，永磁同步电机采用空间电压矢量控制方式，通过检测的霍尔电流信号来进行负反馈PID调节，具有良好的动态响应速度、宽广的调节范围、优异的抗扰特性，从而为绞车张力的快速准确控制提供基础与条件。

张力闭环控制系统由张力控制器、变频器、张力计、PLC等组成，各部件之间由控制总线连接，如图1所示。在电缆张力自动控制模式下，根据测井工艺对电缆张力的要求，输入预设电缆张力值。随着测井工况的变化或电缆绞车滚筒转动，滚筒上缠绕电缆的层数和工作直径在不断变化，电缆线速度和张力也会不断变化。为保持电缆线恒张力，独立分离设置张力计作为张力反馈信号，模糊控制器将根据这个变化实时调整PID参数，调整后的参数传递给永磁同步电机的变频器，控制电机转速，使电缆张力恢复到测井工艺所要求的张力值[9-10]。这种张力模糊控制方式稳定性好，控制的精度高，调节容易，可消除传动误差和摩擦转矩。

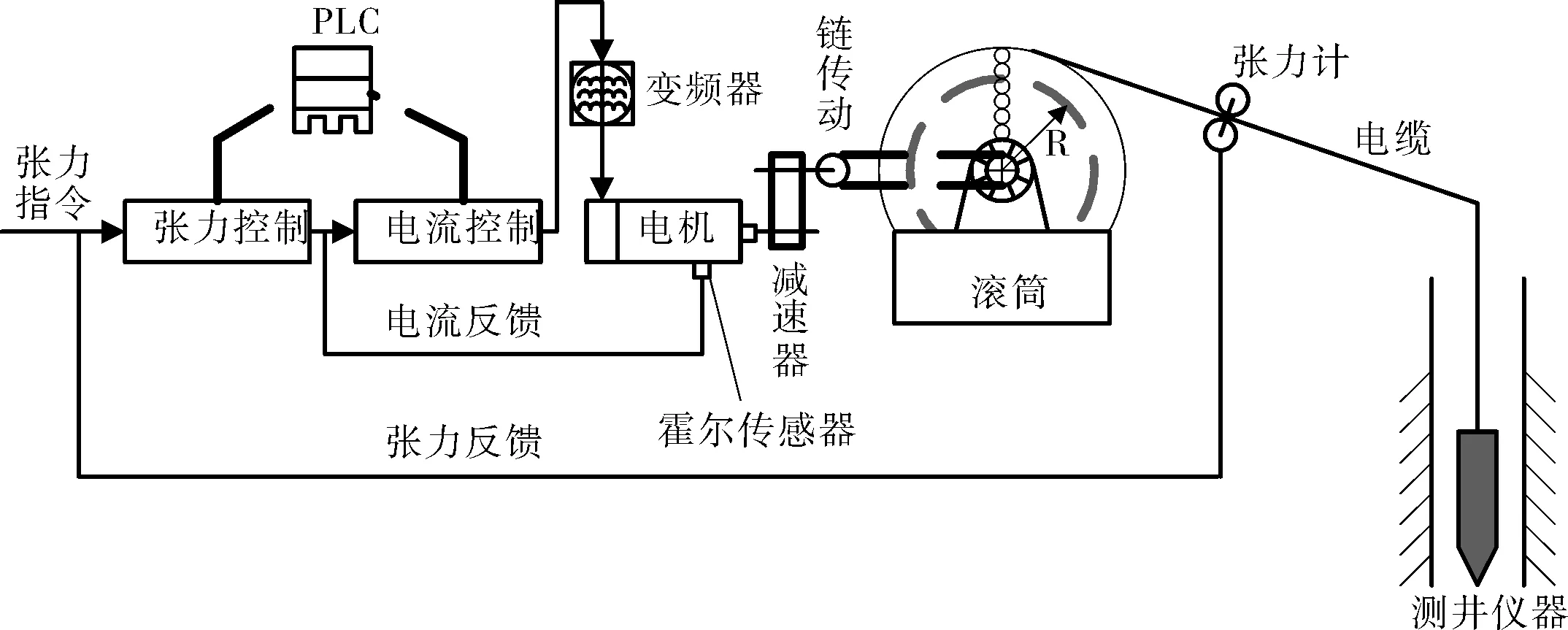
图1 电驱动测井绞车的电缆张力控制系统原理

2 电缆张力系统的数学建模

对测井绞车电缆张力的闭环控制，首先需要建立张力的PID控制数学模型[11-12]。电缆提升时，滚筒的动力学方程为：

(1)

式中：R为电缆缠绕滚筒后的实时半径；ωw为绞车角速度；F为电缆张力；Mw为驱动力矩；Mf为粘性摩阻转矩；Jw为缆绞车的等效转动惯量。

其中，绞车的等效转动惯量Jw主要由电缆和滚筒2部分组成，它随绞车直径的变化而变化。因绞车在运转过程的转速比较低，滚筒的粘性摩阻转矩Mf相比电机输出的驱动转矩比较小，可忽略。

在绞车某一层缠绕中的单位时间dt内，电缆速度为vc，电缆单位长度的质量为ρL，假设滚筒实际半径R不变，绞车的转动惯量变化率为：

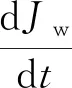
(2)

驱动电机转轴的动力学方程为：

(3)

式中：J为电机的转动惯量；f为电机的粘性摩擦因数；Me为电磁转矩；ML为负载转矩；ω为电机转速。

电机依次通过减速器和链传动将运动传递至滚筒，传动比为j，因此滚筒转速ωw为：

(4)

根据功率相等，从电机到滚筒的总传动效率为η，滚筒的驱动转矩为：

Mw=MLjη

(5)

联立式(1)～(5)，可得电缆张力与电机转速之间关系的控制方程(测井绞车系统的动力学方程)为：

(6)

由式(6)可知，Jw和Me都是与R相关的函数，绞车的实际半径R在电缆提升缠绕过程中不断变化，即，绞车张力控制系统是一个多变量、动态的非线性系统，难以建立精确的数学模型，因此采用近似模型[13-14]。假如在某一层的缠绕过程中，电缆半径变化很小，R可看作常值，将外部载荷F看做外界输入干扰。因此张力控制系统可以看做1个时变(随R的变化而变化)的一阶系统，其传递函数为：

(7)

测量张力的采样环节看做1个延迟环节，延迟时间为Ts，其传递函数为：

(8)

(9)

其中Kw和Cw为常数。

绞车张力PID控制的传递函数为：

(10)

以7 000 m电驱动测井车为研究对象，总缠绕33层，以电缆缠绕的中间位置第17层为近似模型，电缆缠绕17层时的滚筒半径R=0.435 m，其它相关参数为：η=0.87；j=120；J=0.46 kg·m2；f=0.097 N·m·s；Jw=390 kg·m2；ρL=0.526 5 kg/m；vc=0.694 m/s；代入式(9)可得系统开环传递函数为：

3 电缆张力的模糊PID控制

在电缆提升或下放过程重，因电缆绞车张力控制系统受多因素影响，具有不确定性和时变性，难以建立准确的数学模型。由于传统PID控制的参数整定方法存在局限性，如果使用常规PID控制器将导致控制实时性和控制精度较差[15]。模糊控制不需要建立被控对象的精准数学模型，它是基于大量人工操作经验的一种控制方式，因此引入模糊PID控制实现电缆张力的闭环控制，如图2所示。

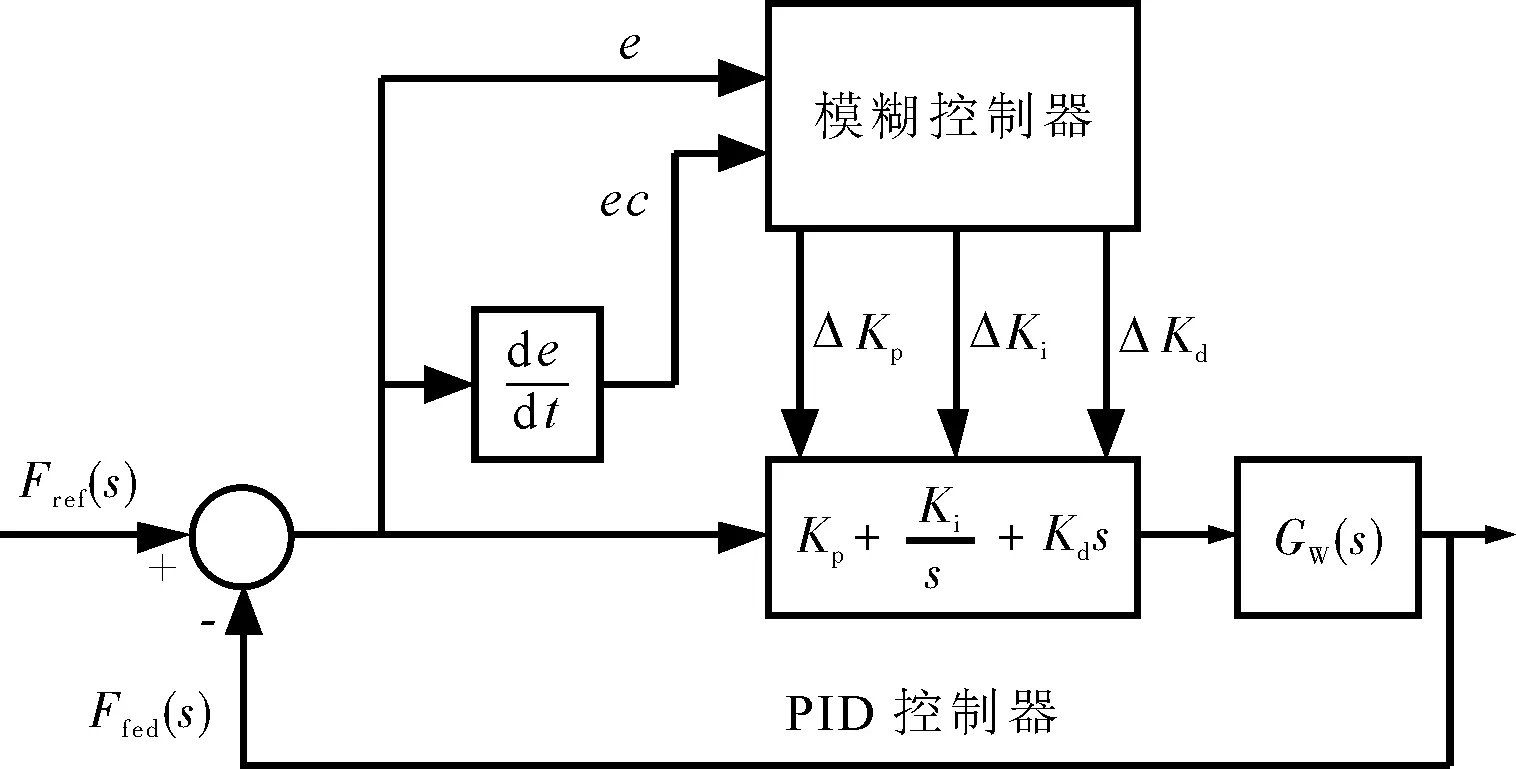
图2 电缆张力模糊PID控制原理图

3.1 模糊控制器设计

模糊控制器的基本结构通常由模糊化、知识库、模糊推理、清晰化4部分组成。

1) 确定输入输出变量。

控制系统输入输出总共有5个变量，以电缆目标张力和实际张力的偏差e，及张力偏差变化率ec作为输入变量，PID校正参数的变化值ΔKp、ΔKi、ΔKd作为输出变量。

2) 确定变量的模糊论域和模糊子集。

输入量e及ec基本论域为[-0.3，0.3]和[-3，3]，输出量ΔKp、ΔKi和ΔKd基本论域为[-1.5，1.5]、[-4.5，4.5]、[-0.15，0.15]。选择模糊状态时要兼顾简单性和控制效果，将输入输出变量的论域划分为{正大(PB)，正中(PM)，正小(PS)，零(ZO)，负小(NS)，负中(NM)，负大(NB)}七档，将E、EC、KP、KI和KD的模糊论域都定义为{-3，-2，-1，0，1，2，3}，对应的模糊子集均为{NB，NM，NS，ZO，PS，PM，PB}。e和ec的量化因子分别为：ke=10，kec=1，ΔKp、ΔKi和ΔKd的比例因子分别为：kp=0.5，ki=1.5，kd=0.05。

3) 确定变量的隶属度函数。

输出变量的隶属度函数反映张力控制系统的控制性能，考虑计算方便、形状简单、灵敏度高等特点，使用三角形隶属度函数。假设与{PB，PM，PS，ZO，NS，NM，NB}对应的高斯基函数的中心值分别为{-3，-2，-1，0，1，2，3}，宽度均为1。

4) 制定模糊规则表。

为准确获取模糊控制器的模糊控制规则，根据e和ec与系统阶跃响应之间的关系，分析PID控制器参数在对应阶段的整定取值大小，并结合绞车工对控制系统PID参数调节经验，总结出专家控制规则及其蕴涵的模糊关系，如表1所示。

5) 模糊推理和清晰化。

选用Mamdani模糊推理方式，依据KP、KI和KD的模糊规则表可将控制规则表述为：

R1： If (e isNB) and (ec isNB) then (KPisPB) (KIisNB) (KDisPS)

其余规则表示依次类推。建立模糊控制规则后，进行反模糊化，将控制器的模糊输出转换为精确的输出量，经过比例因子可以转化为实际作用于控制对象的控制量。清晰化常用的方法有最大隶属度法和加权平均法(重心法)。由于加权平均法具有计算直观且取值平滑的特点，即使对于输入信号发生微小变化的情况，输出也会发生响应，因此采用加权平均法。通过模糊推理和解模糊，得到ΔKp、ΔKi和ΔKd的模糊控制查询表。模糊控制器通过反模糊化计算出PID 3个参数ΔKp、ΔKi、ΔKd变化量，然后根据公式Kp=Kp0+kp×ΔKp，Ki=Ki0+ki×ΔKi，Kd=Kd0+kd×ΔKd求得PID的实际整定参数，其中ΔKp0、ΔKi0、ΔKd0为PID控制器3个调节参数的基准值。得到实际整定参数后，PID控制器便可实现对被控对象的实时控制。

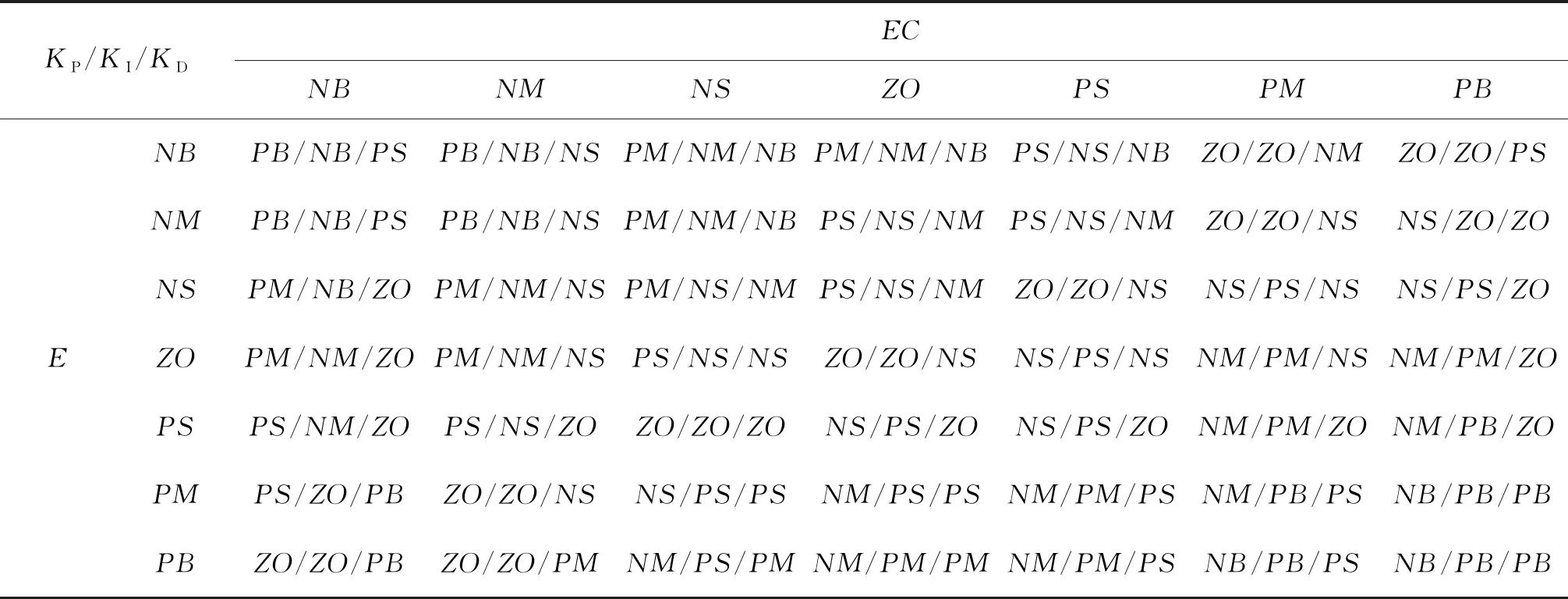
表1 KP、KI和KD的模糊规则表

3.2 模糊控制器的PLC编程实现

电缆张力模糊控制的PLC程序由2个组织块(OB1、OB2)、4个全局数据块(DB1、DB2、DB3、DB4)、3个函数(FC1、FC2、FC3)、1个功能块(FB1)构成，如图3所示。其中，OB1为主程序块，在OB1中编写程序调用功能；OB2为循环中断块，通过该块可以定期启动程序，而无需执行循环程序；在DB1中设置量化因子、比例因子、设定值等一些要用到的变量，在DB2、DB3、DB4数据块中分别输入ΔKp、ΔKi、ΔKd所对应的模糊控制查询表数据；FC1实现信号输入及采样，FC2实现误差和误差变化率的模糊化，FC3实现模糊控制查询表的查询功能；FB1为PID控制功能块。电缆张力控制系统模糊PID控制程序设计流程如图4所示。

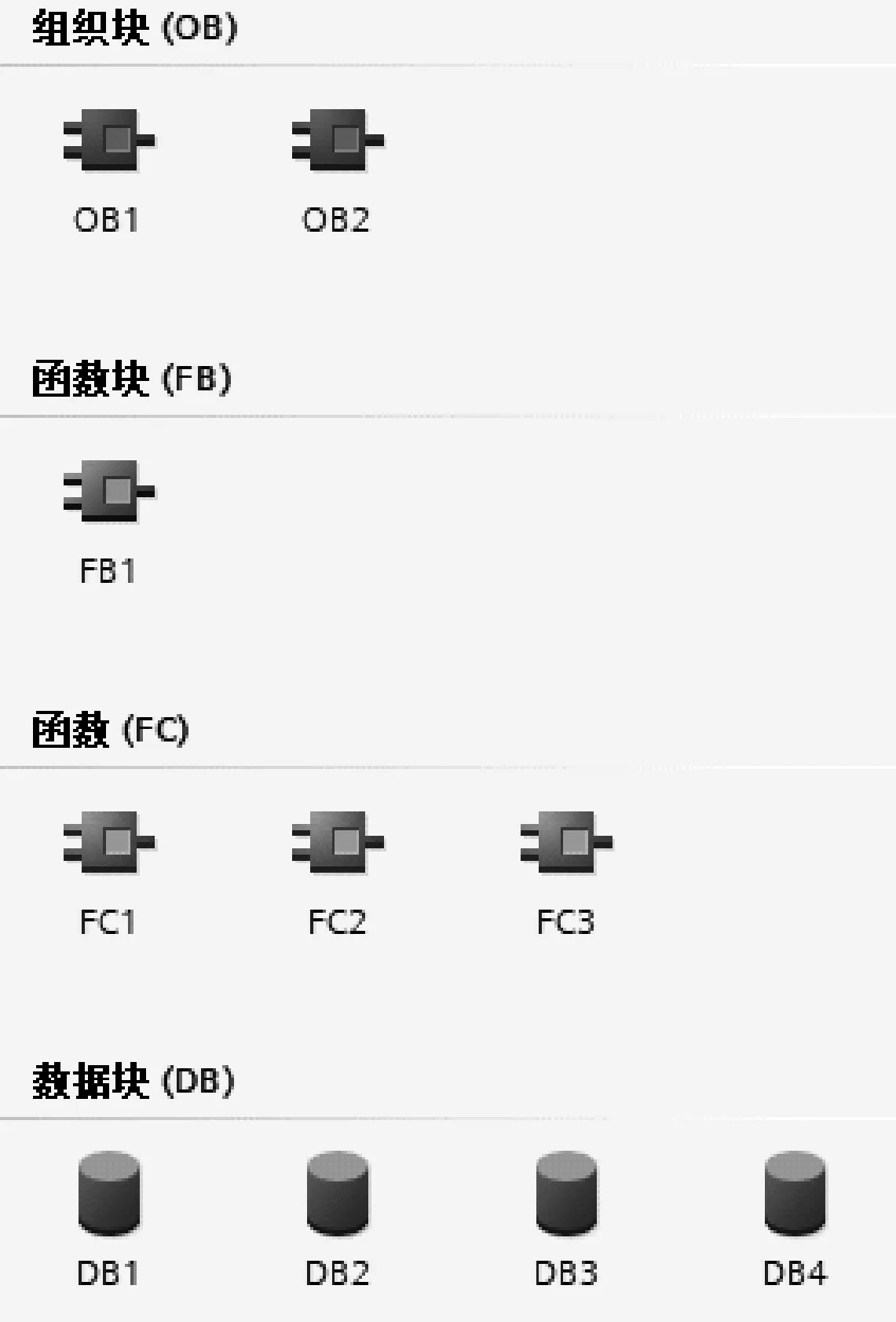
图3 模糊PID的程序结构图

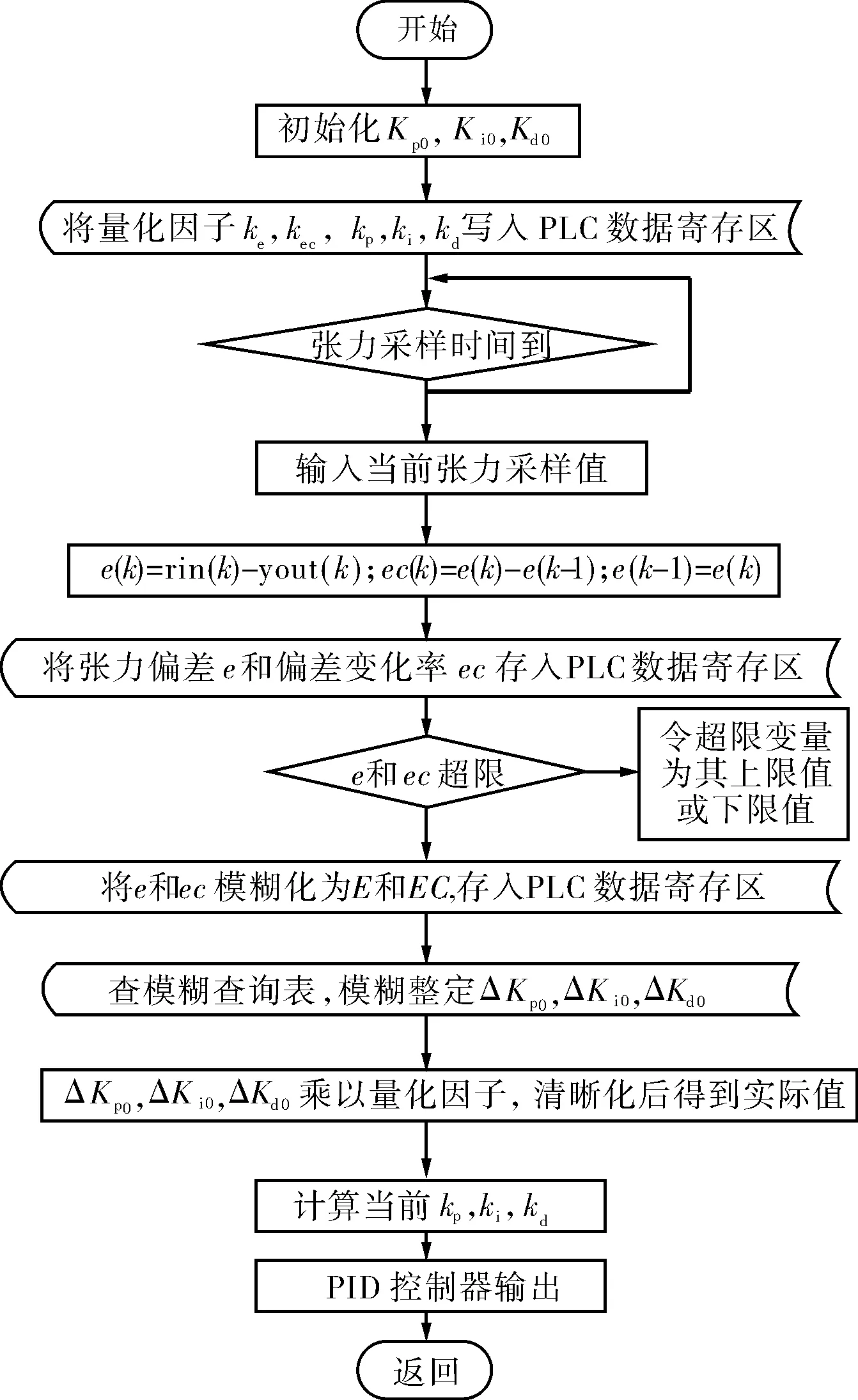
图4 模糊PID控制系统程序设计流程图

4 仿真与结果分析

在Simulink中，根据建立张力控制系统数学模型，搭建张力控制模型，用模糊工具箱做出模糊控制器，并采用阶跃输入信号对提出的电缆张力模糊控制算法的综合性能进行仿真分析，如图5。与常规PID控制比较，模糊控制算法的动态特性如图6所示。由图6曲线可得出，传统PID控制超调量为0.27，上升时间为3.8 s，达到稳定时间为15 s，且产生震荡。常规PID控制系统的超调相对较大，达到稳定时间较长，且系统发生多次振荡，不利于系统的稳定。模糊PID控制的超调量为0.05，上升时间为1.6 s，达到稳定时间为8.4 s。模糊PID控制系统的超调量较小，上升时间较常规PID控制系统短，虽然产生多次振荡，但较快进入稳定状态。说明所建立的电缆张力控制系统具有较快的响应时间和收敛能力，良好的稳定性。

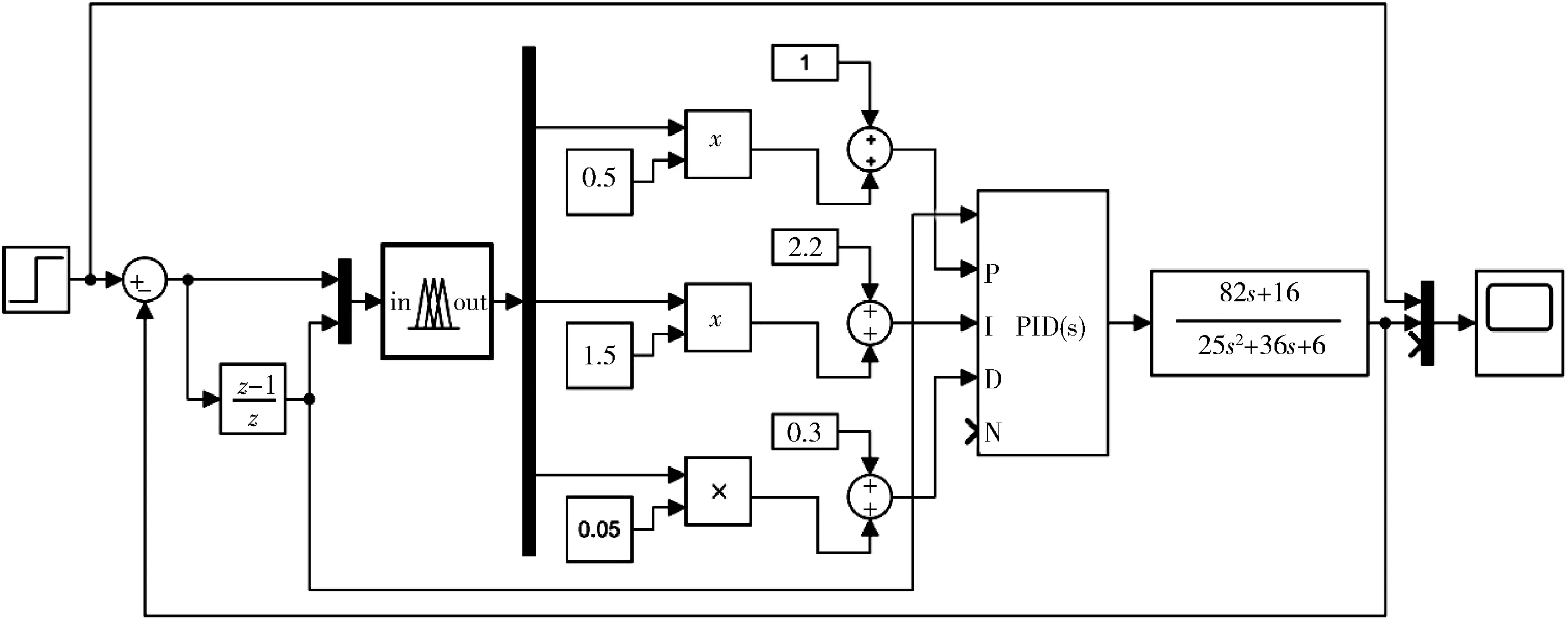
图5 电缆张力控制系统Simulink模型结构图

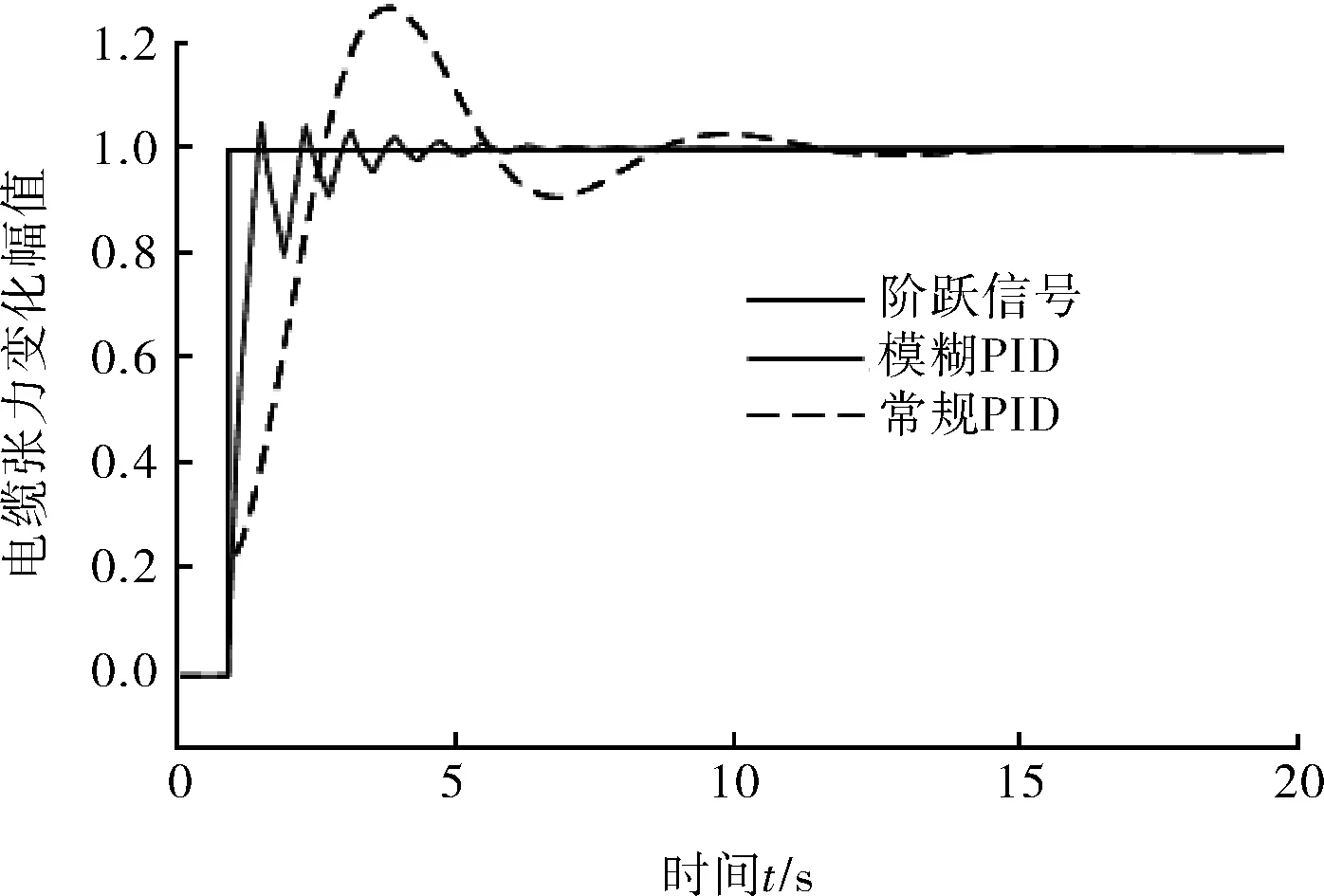
图6 电缆张力常规PID控制和模糊PID控制仿真曲线对比

5 结论

1) 电驱动绞车电缆张力的控制系统属于典型的非线性时变控制系统，通过建立绞车张力控制的动力学近似数学模型，应用模糊控制的原理，可实现电缆张力PID的参数自整定。

2) 仿真分析表明，模糊控制较常规PID控制具有更好稳定性和更高控制精度，验证了电缆张力智能控制算法的可行性。

3) 在PLC平台上设计模糊PID控制算法程序，为电缆绞车的张力智能控制工程应用奠定基础。