分数阶双参数Maxwell流体自然对流与传热传质的L1/有限体积法

赵金虎

（阜阳师范大学 数学与统计学院，安徽 阜阳 236037）

0 引言

非牛顿流体广泛存在于日常生活和自然界中，比如油漆、牛奶、泥浆、高分子溶液、聚合体、生物体的血液、细胞液等［1］.随着现代科技的发展，非牛顿流体力学的研究理论在许多工业生产和应用科学领域都有重要应用，并对工业的发展具有重大的现实意义［2］.粘弹性流体是非牛顿流体的一种，在剪切流场中，这种流体在外力作用下发生形变或流动，当外力消除后，它的形变会随时间恢复或部分恢复［3］.近年来，分数阶模型凭借灵活多变的非局部性质在非牛顿流体的粘弹性动力学表征方面获得广泛的应用［4-7］.Feng等［8］提出平行平板中非牛顿流体流动的隐式有限差分格式，验证分数阶线性方程组的稳定性和收敛性.Yang等［9］研究矩形微通道中分数阶Maxwell流体的电渗流动，使用谱方法有效解决该模型的控制方程组.Zhang 等［10］考虑矩形管中分数阶Maxwell 磁流体在变压强梯度下的二维流动，求得分析解和数值解，并作对比.Bai等［11］分析双向伸长板上的分数阶Maxwell流体的流动与传热传质，采用有限差分方法求解非线性方程组，收敛精度与数值特例进行验证.Rasheed等［12］讨论分数阶粘弹性流体流动过程中的化学反应作用，从数值结果分析反应物的存在对流动的显著影响.Ahmed［13］研究多孔介质方腔中纳米流体的对流作用，引用分数阶Darcy模型，模拟纳米混合物的波形流动.更多有关分数阶模型的应用，详见文献［14-19］.

在关于分数阶粘弹性流体流动与传热的数值理论研究中，很少有文献使用有限体积方法求解非线性的分数阶控制方程.鉴于此，本文拟结合有限体积方法与分数阶L1格式，用于求解分数阶粘弹性流体的自然对流与传热传质问题.分数阶双参数Maxwell模型与流动的动量方程相结合，建立强耦合非线性且含有多项时间分数阶导数的边界层控制方程组，最后获得数值解并进行分析.

1 控制方程

考虑竖直平板上粘弹性流体的自然对流与传热传质（受到热和浓度的浮升力作用），温度方程加入粘性耗散和放射吸热，浓度方程也包含热泳迁移和化学反应.除密度变化符合Boussinesq′s假设，流体的其他性质均设定为常数.平板分别控制在常数温度Tw和常数浓度Cw，且远离平板足够远处的温度T∞和浓度C∞非常小.在边界层流动中，粘弹性流体的本构关系采用分数阶双参数Maxwell模型［20］：

其中τxy是剪切力分量，ε是剪切应变，ε̇=dε/dt是剪切速率，G是剪切模量，λ=μ/G是松弛时间，α和β分别是剪切力和剪切应变的分数阶导数参数，∂α/∂tα是Caputo型分数阶导数算子［21］：

其中Γ(·)是Gamma函数.

强耦合的动量、温度和浓度的无量纲控制方程分别为

其中：u和v分别是x轴方向（沿着竖直平板）和y轴方向（垂直于平板）的速度分量，T是温度，C是浓度，Gr是Grashof 数，Gm是浓度的Grashof 数，Nr是浮升力比值，Pr是Prandtl 数，αf是热扩散系数，Ec是Eckert数，Ql是放射吸收系数，Sc是Schmidt数，ψ是热泳系数，γ是化学反应参数.本文由于篇幅有限，只建立分数阶的控制方程组，各无量纲参数的物理意义参见文献［22］.

无量纲的初始条件和边界条件为：

2 数值方法

本部分介绍求解分数阶控制方程组的有限体积方法.为获得单个控制单元上控制方程的数值积分，把计算区域划分为离散的控制系统，如图1所示，其中P为中心节点.然后，在单个控制体积以及有限时间步长Δt下对方程组进行积分.最后可以得到关于每一个节点P的离散差分方程.

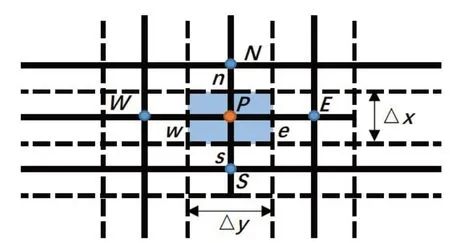
图1 网格系统的控制单元

从方程（3）开始，首项关于时间的导数通过向后差分格式进行离散，得到：

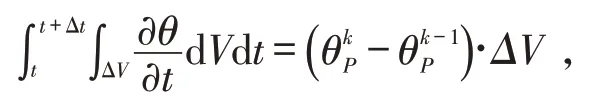
其中ΔV=Δx·Δy是控制单元的体积，Δx和Δy分别是空间步长.

对流项的体积积分通过高斯公式转化为面积分，并且采用一阶迎风差分格式进行近似：

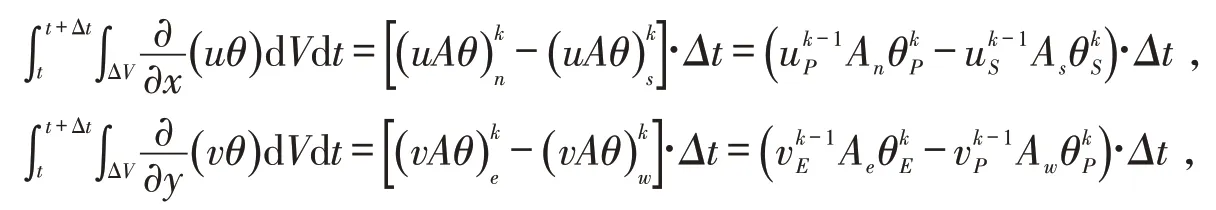
其中A表示控制体积的表面积，Aw=Ae=Δx，An=As=Δy.

右端的扩散项通过中心差分格式进行离散：

粘性耗散的二次项经过线性化处理后离散为：

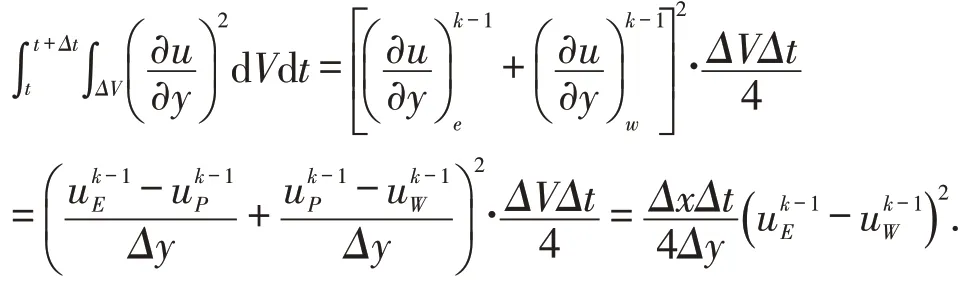
单项浓度采用半隐格式进行积分：

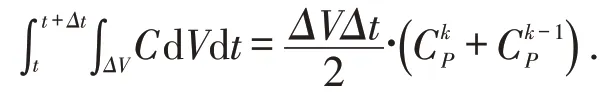
方程（2）和（4）中的整数阶导数采用相似的过程进行处理.特别地，方程（4）右端的热泳作用项的积分为：

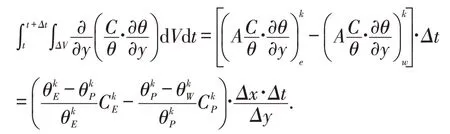
对于ω（0＜ω ＜1）阶的时间分数阶导数，本文引用L1近似格式进行离散［23］：

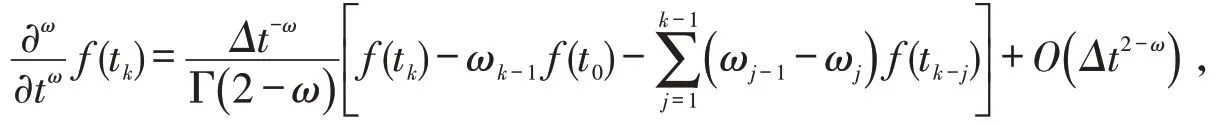
因此，方程（2）中的多项时间分数阶导数的积分结果为：

最终获得内节点P处的迭代差分方程：

其中φ可以代表速度、温度或浓度.例如，关于速度差分方程的各项系数为：

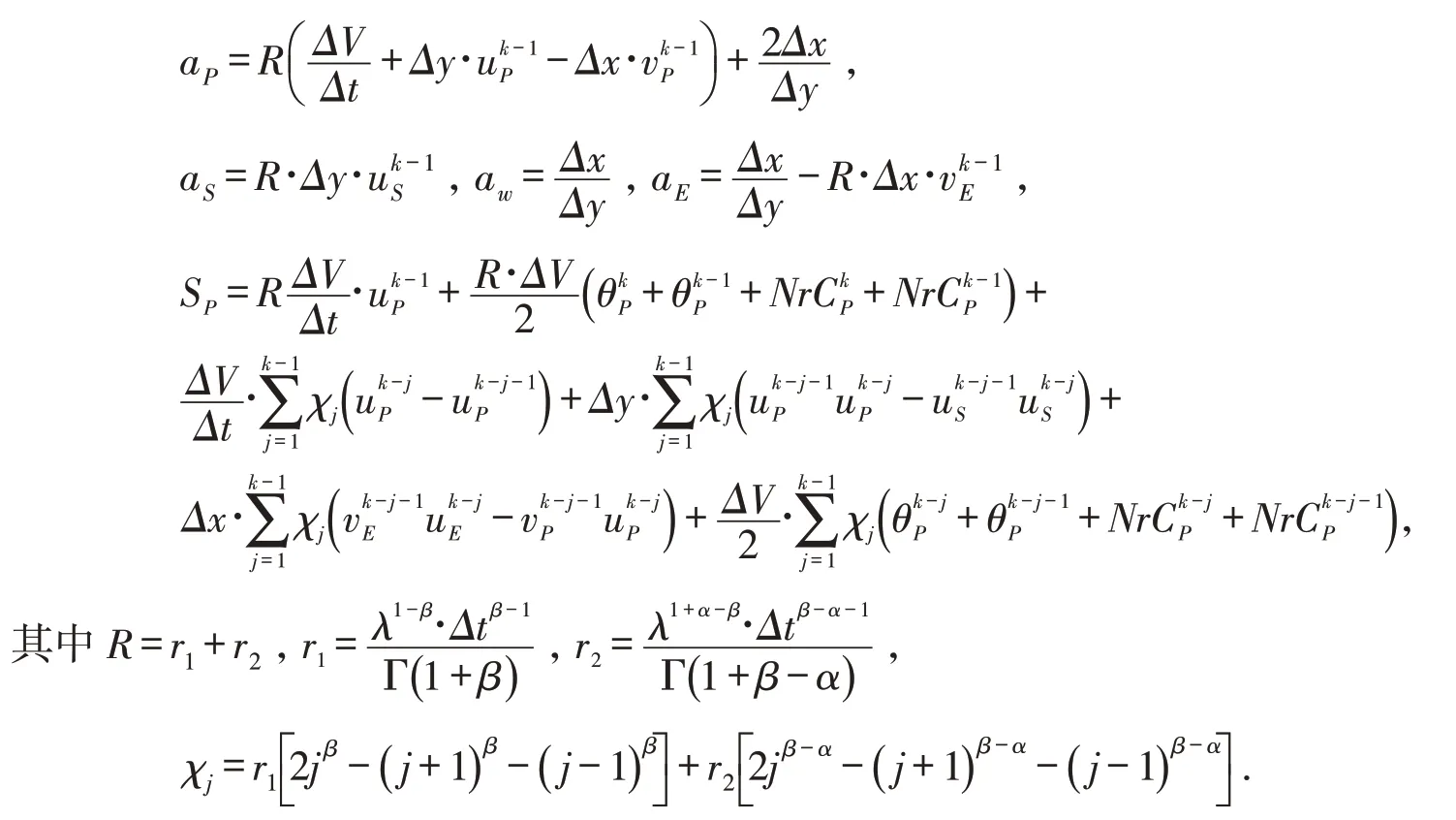
为获得y轴方向速度分量的数值解，对连续性方程（1）进行积分得到：

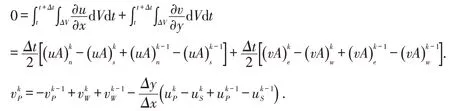
最后，获得内节点P的迭代差分方程组.迭代截断误差控制在10-4以内，计算区域的2个边界长分别为Xmax=1 和Ymax=20，其中Ymax对应于y→∞且位于速度边界层之外.为平衡数值解的精度和计算耗时，网格数选定为M=20，N=200，时间步长控制为Δt=0.1.图2给出当空间网格数分别加倍时，同一组参数下的速度分布吻合良好.结果表明，本文选取的网格步长适合计算.特别指出，本文提出的有限体积方法数值格式是条件稳定的，当网格步长的比值超过一定范围时，数值解不稳定.

图2 网格无关性验证

3 结果讨论

图3和图4给出分数阶导数参数α对数值结果的影响.图3表明，随着α的增加，垂直速度u增大，且边界层厚度也增加.α=0 表示分数阶二阶流体，具有最小的速度分布.这个结果表明，流体采用分数阶模型时，随着粘弹性的增强，表现出剪切增稠的特性.图4表明，温度分布随着α的增加而略微减少，这与图3中α对速度的作用刚好相反.

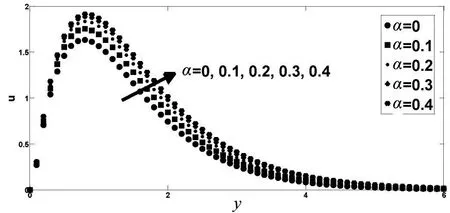
图3 不同α 下的速度分布

图4 不同α 下的温度分布

图5~7给出分数阶导数参数β对数值结果的影响.在图5中，随着β的增加，速度分布呈现明显减少的趋势，且边界层的厚度减少.这个结果与图3中α对速度的作用截然相反，这是因为分数阶模型中剪切力和剪切速率的分数阶参数异号，当分数阶参数小于0时表示的是分数阶积分.当β=1时表示单参数的Maxwell模型，该模型具有最小的速度分布和边界层厚度.图6和图7分别给出β对温度和浓度分布的影响.随着β的增加，温度和浓度均显著增加，且传热和传质边界层厚度也增大.

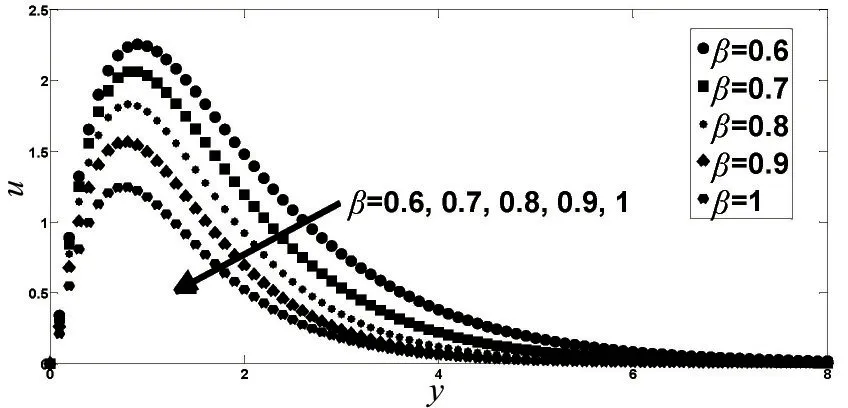
图5 不同β 下的速度分布

图6 不同β 下的温度分布

图7 不同β 下的浓度分布

4 小结

本文结合有限体积方法和分数阶L1格式，求解分数阶双参数Maxwell 模型的边界层控制方程组，结果表明，剪切力和剪切应变的分数阶导数参数对数值解的作用相反.对于本文建立的强耦合非线性的分数阶控制方程组，目前研究还很难求出解析解，所以无法给出稳定性和收敛性的证明，这些问题将在下一步的工作中解决.