高土堤加筋土工格栅受力状态及滑坡分析*

郑鑫超，段彦福，宋 玲

(1.西京学院 土木工程学院，陕西 西安 710123；2.西京学院 陕西省混凝土结构安全与耐久性重点实验室，陕西 西安 710123；3.石河子大学 水利建筑工程学院，新疆 石河子 832061)

0 引言

在实际工程中，高土堤典型的破坏形式主要是滑坡，所以对高土堤加筋土工格栅受力状态与滑坡关系的研究是非常有必要的。土工格栅加筋土堤、边坡在土工格栅受力和滑坡方面的研究，主要有数值模拟[1]、离散元法[2]和模型试验[3]，国内学者唐晓松等[4]采用双强度折减法对加筋土边坡稳定性进行了分析；胡幼常等[5]采用影响带观测的方法分析加筋土坡的稳定性；王志兵等[6]对膨胀土边坡渠道中采用土工格栅滑坡进行了分析；王家全等[7]、刘华北等[8]通过实验和理论研究分析了加筋土挡墙长期变形和内力特征；沈华章[9]通过本构模型及矢量和分析法，分析了边坡渐进性破坏过程。Yu等[10]通过模型试验，分析了动力作用下地震加筋边坡的内部稳定性；Balakrishnan等[11]采用离心模型试验对边缘回填土工格栅加筋土墙进行了试验研究；Costa等[12]对土工织物加筋土墙的时变特性的离心进行了评价。

从现有国内外研究内容和成果中可发现，就实体工程而言，多数学者对于土工格栅加筋土的研究没有结合实体工程；就研究方法而言，多数学者没有结合实测数据进行分析，导致高土堤加筋土工格栅受力状态与滑坡方向关系方面的研究较少，土堤中的土工格栅受力状态和受力分布大小与滑坡方向关系也尚不明确。因此，本文通过理论分析、数据监测、建立数值模型，分析高土堤加筋土工格栅受力状态对滑坡及滑坡方向的影响，拟为相关工程实际问题的解决提供参考和借鉴。

1 工程概况

土堤坡面材料主要为加筋绿色格宾，坡体内采用柔性土工格栅，级配碎石土填筑，由高30 m和高20 m的土堤组成，坡比均为1∶0.364，如图1所示。其中高30 m土堤体分3级填筑，如图1(a)所示，高20 m高土堤分2级填筑，如图1(b)所示，实体工程如图1(c)所示。

图1 土堤截面及工程实体Fig.1 Earth embankment cross section and engineering entity

2 土工格栅受力状态分析

2.1 格栅理论计算

3种土工格栅的设计抗拉应力分别为62，383，450 kN/m2。目前，解释土工格栅加筋与填土之间力学特性主要有2种观点：第1种观点认为土工格栅和填土之间相互独立，是1种组合材料；第2种观点认为土工格栅和填土是组合而成的整体。土工格栅与填土之间存在摩擦力，所以用摩擦理论进行分析研究[13-16]。本文选择使用第1种观点，通过式(1)可算得第i层土工格栅所受拉力Ti：

(1)

式中：Sx，Sy分别为拉筋之间水平间距和垂直间距，m，在计算时只考虑水平方向间距Sx，不考虑垂直方向间距Sy；σs为土工格栅的拉应力，kN/m2；As为土工格栅的截面积，m2；φ为填土的摩擦角，(°)。

由式(2)算得最大拉应力σhi：

(2)

式中：σhi为土工格栅最大拉应力，kN/m2；Ti为第i层拉筋的计算拉力，kN；K为拉筋拉力峰值附加系数，取1.8。

2.2 格栅拉应力大小

通过式(2)可得到3级土堤和2级土堤每1层土工格栅所受最大拉应力，如图2所示。图2(a)，图2(b)所示分别为2级土堤40层和3级土堤60层土堤土工格栅每1层从上到下的受力大小。由图2(a)，图2(b)可以看出，高20 m土堤的土压力呈直线增长模式，而高30 m土堤在第2级土堤处突然增大，这是因为3级土堤第1，2级填土土压力大小比较均匀，到第3级时累加，可得到随着土压力的增大土工格栅的拉力也增大。

图2 土工格栅拉应力Fig.2 Tensile stress of geogrid

2.3 土工格栅现场受力监测

高30 m和高20 m土堤数值模拟及其监测元件横断面布置如图3所示。根据分析计算选定有代表性的格栅加筋层安装一定数量的专用柔性位移计测量土工格栅的拉力，采用综合测试仪监测施工完工后土工格栅的拉应力沿土工格栅长度方向的分布情况。柔性位移计分别布置在3级土堤和2级土堤相应位置上，其中30 m高土堤布置于第9，20，30，39，50层土工格栅上；20 m高土堤布置于第9，20，30，39层土工格栅上。

图3 土堤数值模型及监测元件横断面布置Fig.3 Numerical model of earth embankment and cross-sectional layout of monitoring components

施工结束后结构自身的重力不变，作用在柔性位移计上土颗粒有所滑动，这种滑动造成柔性位移计位移，从而可得出土工格栅的受力大小。从连续观测数据看，每一次观测的数据变化不大，结构横截面中心处的土工格栅拉力最大，两边较小，原因有2个：1)土堤两侧填土水平位移时对土工格栅施加了拉力；2)土堤截面中心处的竖向土压力最大。

3 土工格栅受力数值分析

3.1 建立数值模型

按照与实体工程1∶1比例建立二维模型，3级土堤和2级土堤数值模型分别如图3(a)，图3(c)所示。该模型由4部分组成：第1部分为回填土层，第2部分为3种抗拉强度不同的土工格栅，第3部分为1.5 m厚的换填层，第4部分为自然土层。材料参数通过项目地勘报告，类似土样与土工格栅复合体的大型三轴试验结果得到[17]。4部分材料属性见表1，土工格栅截面和接触特性参数见表2。

表1 材料属性参数Table 1 Parameters of materials properties

表2 土工格栅截面和接触特性参数Table 2 Parameters of geogrid section and contact characteristics

3.2 监测点设置及模拟

为分析比较结构内部不同高度处土工格栅的应力大小，分别在高30 m土堤和高20 m土堤模型的土工格栅上设置与实体工程中相同的监测点，高30 m土堤模型的监测点从A1～A40如图4(a)所示，高20 m土堤模型监测点从B1～B20如图4(d)所示。

3.3 格栅受力模拟分析

结构中的土工格栅依靠Midas GTX NX软件设置接触面与填土产生作用，它们之间应力也依靠设置的接触界面传递，从而可以测得土工格栅的内力。图4(b)为高30 m土堤土工格栅应力，图4(e)为高20 m土堤土工格栅应力，由图4(b)和图4(e)可看出，每1层监测点越靠近土堤截面中心，土工格栅的内力越大，而靠近两侧土工格栅受力越小，这种情况的出现一方面与土压力重心处受力有关，另一方面是由于施工结束后重力作用下填土向两侧分散。模拟监测值与实际监测值的大小基本接近，说明模拟结果相对可靠，监测值也基本符合实际。

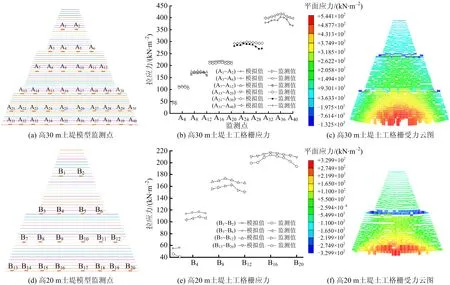
图4 土堤数据监测及受力云图Fig.4 Data monitoring and stress cloud map of earth embankment

从图4(c)和图4(f)可以看出，土工格栅应力由上到下增大，底部最大，这与实际监测的受力大小分布情况基本一致。

4 土堤滑坡方式分析

边坡和土堤的稳定性分析目前大多采用极限平衡法和强度折减系数法[4-6]，对土工格栅受力状态方面考虑较少。无论是自然滑坡还是地震滑坡，滑坡首先从结构的薄弱环节开始，所以从土工格栅受力状态的角度和数值模拟来分析土堤薄弱环节的滑坡，其滑坡形式有以下3种：第1种为从第1级开始滑坡，第2种为从第2级开始滑坡，第3种为从第3级开始滑坡，这3种由于土工格栅的局部断裂而造成的滑坡，其特征是某一层的土工格栅发生断裂导致，发生中间鼓起式的滑坡。因为高30 m土堤比高20 m土堤土工格栅受力更大，所以本文选择高30 m土堤为研究对象。

4.1 倾斜造成的滑坡

由于施工难度大，填土厚度误差体现在结构的倾斜度上，当土堤倾斜时两侧土压力不平衡，因此，土工格栅所受的拉拔力更大，倾斜程度不同，土工格栅受力的状态及力的大小分布情况不同，在长期土压力不平衡下，局部土工格栅可能提前进入疲劳期，导致土工格栅破坏，从结构整体来看土工格栅的受力状态为倾斜内侧最大，外侧最小。为研究不同倾斜度下土工格栅的受力以及受力状态对滑坡的影响，建立倾斜度分别为5°，10°，15°的数值模型，得到土堤应力云图及分布曲线如图5所示。其中模型的材料属性、网格大小、模拟条件与3.1相同。

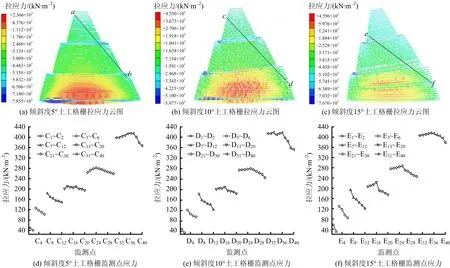
图5 不同倾斜度土堤应力云图及应力曲线Fig.5 Stress cloud diagram and stress curves of earth embankment with different inclinations

在施工过程中，由于施工工艺、测量、碾压等误差，容易造成土堤倾斜，首先假设倾斜度为5°，建立模型，通过静力分析得到土工格栅的受力状态如图5(a)所示，可以看出土堤偏移导致土工格栅的整体拉力从右向左增大，ab线左右的拉力有明显不对称，并且底部最大拉力向左偏移。为了监测在该种状态下模型中土工格栅的拉应力，在模型的历程分析中设置监测点C1～C40(监测点位置与图4(a)相同)，得到土工格栅监测点应力分布曲线如图5(d)所示，从具体的数值中可得到土工格栅受力同样为整体拉力从右向左增大。

为进一步分析在一定倾斜度下土工格栅的受力状态，建立倾斜度为10°的模型。在模型的历程分析中设置监测点D1～D40(监测点位置与图4(a)相同)，通过静力分析得到土工格栅的受力状态云图如图5(b)所示，可看到土工格栅的拉力同样从右向左增大。底部最大土工格栅的拉力继续向左偏移。图5(e)为土工格栅监测点应力分布曲线，通过与倾斜度为5°的土工格栅测点应力对比，发现二者变化规律基本相同。

为了解越倾斜是否土工格栅的拉力依然为左边大右边小，继续建立倾斜度为15°的模型，在模型的历程分析中设置监测点E1～E40(监测点位置与图4(a)相同)，以便于监测在该种状态下土工格栅的拉应力。对该模型依然进行静力分析得到土工格栅的受力状态云图如图5(c)所示，可以看出土工格栅拉力最大偏移斜率ef继续减小。从而可以得到随着土堤的倾斜度越来越大，土工格栅的拉力从左到右，从下到上呈1条斜线的趋势减少。

从图5(a)～(c)和图5(f)来看，随着倾斜度的增加，ab线、cd线、ef线的斜率越来越小，从右到左、从上到下拉应力越来越大，随着倾斜度的增大模型中监测点的拉应力同样从右到左、从上到下越来越大。当倾斜度不大时第1级有可能发生滑坡，随着倾斜度增大，第1级、第2级、第3级都可能发生滑坡，滑坡时倾斜方向区域以内黏聚力、摩擦角、土压力持续增大。传统的土堤设计为从上到下土工格栅的强度增大，但是通过对图5分析可知，在设计时土堤两侧的土工格栅强度也应适当增大。

4.2 工格栅渐进破坏造成的滑坡

当土工格栅在施工或者生产时产生局部损伤，该部分比较薄弱，在受到更大的拉拔力时被拉断，此时填土失去约束，土压力失衡，有可能发生单侧滑坡，此时塑性区贯穿作为滑坡的必要条件，该滑坡首先由小面积的滑坡再到大面积的滑坡。根据数值分析可得，滑坡有可能从第2级开始，也有可能从第3级开始，而滑坡由第几级开始，根据4.1中分析，完全取决于倾斜度。从第2级发生滑坡的滑裂带如图6(a)所示，从第3级发生滑坡的滑裂带如图6(b)所示。

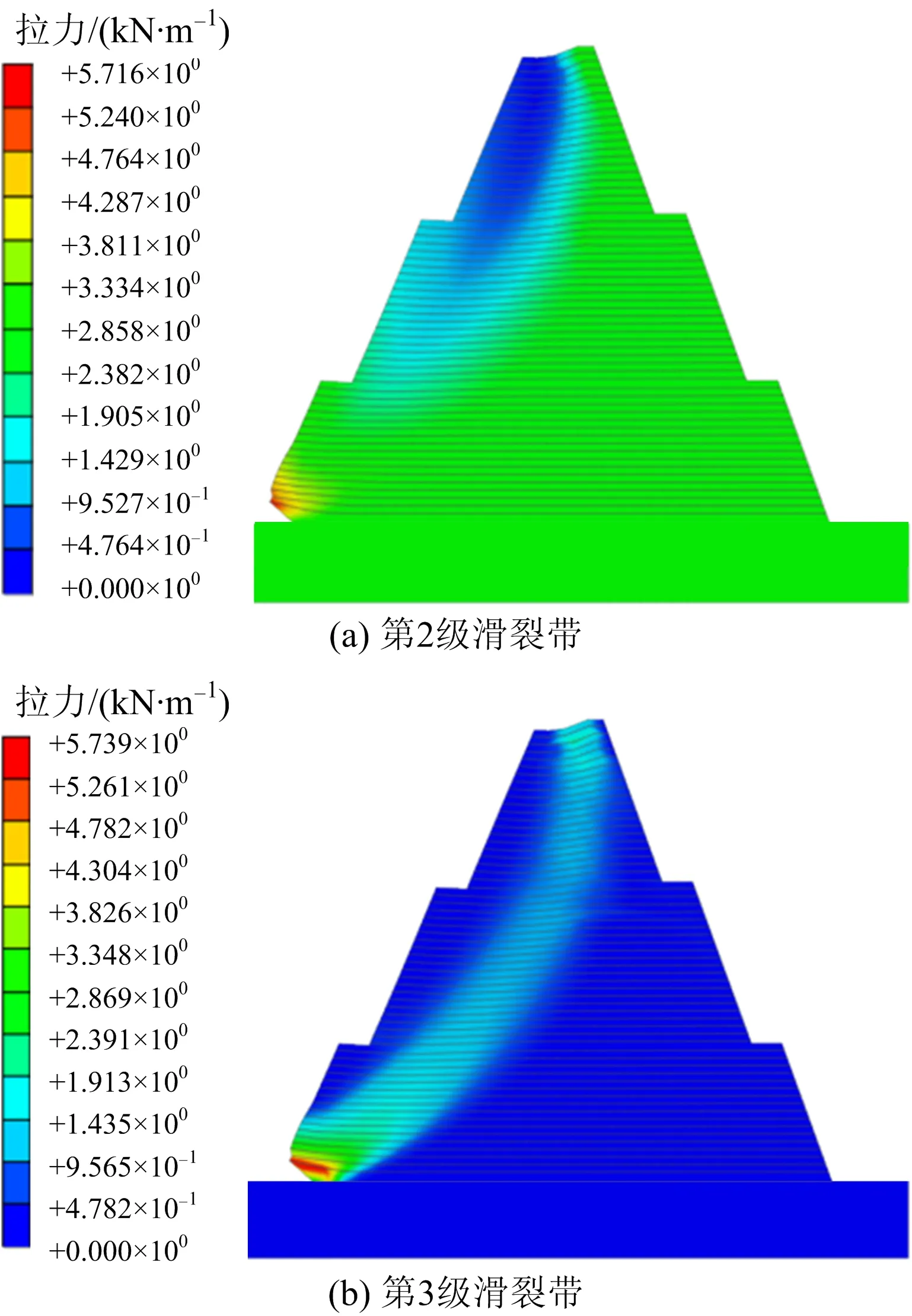
图6 滑裂带Fig.6 Fracture zone

根据毕肖普法滑坡分析法，结合渐进破坏规律，土堤不同部位的渐进破坏都会造成第1级、第2级、第3级坡脚处首先破坏而形成的塑性区，在塑性区填土的摩擦角和黏聚力减小，塑性区上、中、下部土工格栅拉力也持续增大，土工格栅在这种拉力的长期作用下，最终发生滑坡，第3级塑性区如图7所示。

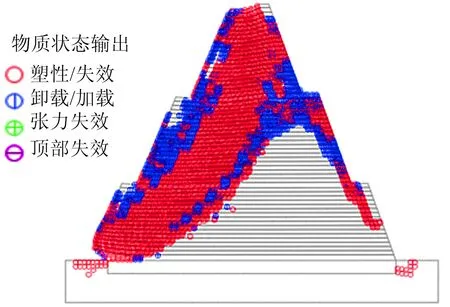
图7 第3级塑性区Fig.7 Third-order plastic zone

5 结论

1)通过理论分析、数据监测、数值分析发现，台阶底部两侧的土工格栅应力较大，而在实际设计中此部位土工格栅的抗拉强度与中间部分相同，此设计滑坡时每个台阶的坡脚处容易破坏，所以设计时每个台阶坡脚处土工格栅强度建议加强。

2)土堤随着倾斜度的增加，从右到左、从上到下拉应力越来越大，在倾斜时边侧某层的土工格栅有可能断裂，对提前预测土堤的滑坡方向和滑坡的趋势以及滑坡的破坏形态具有指导意义。

3)滑坡时倾斜方向区域以内黏聚力、内摩擦角、土压力持续增大，倾向方向区域以外相反。传统的土堤设计为从上到下土工格栅的强度增大，但是通过受力云图和监测曲线可知，土堤边侧土工格栅的拉力也较大，所以在设计时土堤两侧的土工格栅强度也应适当增大。