基于迭代校正的病例临床复杂度度量方法研究
陶丽, 王纯青, 张自力, 陈波
1.西南大学 计算机与信息科学学院,重庆 400715;2.重庆医科大学 附属第一医院,重庆 400700
随着信息技术的发展,包括医疗在内的众多行业涉及到对高维稀疏数据的学习和处理.比如,医院住院病人病案首页数据中包含大量的合并症、并发症数据,如何基于这些高维、稀疏的症状信息对病人病情严重程度进行评估从而实现住院费用预测,是当前我国能否成功推行以疾病诊断相关分组(diagnosis related groups,DRGs)为核心的付费制度面临的关键问题.
通过数据特征提取(feature extraction)实现特征降维、获得信息含量更加丰富的新特征是有效处理高维稀疏数据,提升特征利用效能的重要手段.在特征工程中,主成分分析(principal components analysis,PCA)[1]及其变种[2-11]是提取高维稀疏数据的主要信息或生成与目标相关性更高信息的主要方法.但是作为无监督的特征提取方法,主成分分析难以将提取的新特征与问题目标相关联,且降维后的新特征对于单个样本缺少可解释性,不太适用于本文例示的应用问题.线性判别分析(linear discriminant analysis,LDA)和核线性判别分析(kernel LDA)[12-13]也是处理结构化高维稀疏数据的常用方法.这类方法通过将数据投影到具有最佳分类性能的方向,实现数据降维.但是,这类方法适用于二分类或者多分类问题,不太适用于因变量为连续型(如住院费用)的特征提取.
本文受医疗管理领域的病例临床复杂度(episode clinical complexity,ECC)模型[14]启发,提出了一种基于迭代校正的高维稀疏特征提取方法.ECC模型是澳大利亚学者提出的根据病例诊断情况和个体特征构建治疗复杂程度新特征的方法[15].现有ECC模型在提取病例诊断复杂水平这一特征时,主要考虑了不同特征数(即不同诊断数目)对结果(即病例诊治费用)产生的影响,但对特征类型(即诊断类型)对结果的影响考虑不充分.本文提出的基于迭代校正的ECC改进模型(iteration-based ECC,IECC)可以在因变量的监督之下构建能够同时体现特征数目和特征类型差异的新特征.将IECC模型应用于重庆某大型三甲医院2015-2019年呼吸系统和循环系统病案首页数据的实验分析结果表明,本文所提方法得到的病人病情复杂程度的新特征与病人住院花费具有更强的相关性,说明IECC模型是一种适用于解决类似高维稀疏数据特征提取的有效方法.
1 相关研究
1.1 高维稀疏数据特征抽取方法
主成分分析(PCA)[1-6]能够把高维变量进行降维处理,从而实现主要特征提取.但实验结果同时表明,数据稀疏程度会对主成分分析这类方法的特征提取性能造成较大影响[8].
针对这一问题,一些研究者提出了面向稀疏数据的PCA算法[9-11].但是PCA族群的算法均属于无监督的特征提取方法,在特征提取过程中难以将提取的新特征与问题目标相关联,得到的新特征也缺乏可解释性,在现实应用中具有一定局限.
线性判别分析(LDA)[12]是另一类常用的有监督特征提取方法.文献[13]提出的核线性判别分析方法可通过计算特征空间内积将数据从高维映射到低维子空间,但这种方法存在计算开销巨大的弊端.同时,线性判别分析这类方法主要适用于二分类或者多分类问题,当目标类别具有非正态或多峰混合分布时,或者数据具有高维特征时,该方法表现不佳[16].
1.2 病例临床复杂度模型
病例临床复杂度模型ECC是澳大利亚评估患者诊疗复杂程度的一种常用方法[14].该模型从医疗资源消耗角度,以住院费用为监督,基于病例的合并症、并发症情况对其病情复杂程度进行度量.度量算法的核心步骤包括:① 建立合并症、并发症数目与住院费用的关系模型;② 通过测算有无某诊断时费用的相对变化测算该诊断的费用贡献,从而获得每个诊断的复杂程度(diagnosis complexity levels,DCL);③ 基于诊断复杂程度(DCL),综合某病例的所有诊断,得到该病例的临床复杂度评分(episode clinical complexity score,ECCS).
目前,虽然ECC模型已得到广泛应用,但是,ECC模型在度量病例诊断复杂水平时,主要考虑了病例的诊断数目对住院费用产生的影响,但对相同诊断数下不同诊断类型对住院费用的影响考虑不充分,有待进一步改进.因此,本文提出基于迭代校正的病例临床复杂度改进模型(iteration-based ECC,IECC),通过在费用估计和诊断复杂程度的度量过程中考虑诊断类型的影响,使得临床复杂度评分ECCS能够更好地反映资源消耗差异.
2 基于迭代校正的病例临床复杂度改进模型(IECC)
基于迭代校正的病例临床复杂度改进模型(IECC)主要包含3个步骤.
步骤1:住院费用与诊断数目关系模型学习
由于医疗资源消耗与诊断数目在临床中不符合线性关系,因此,模型沿用原ECC模型假设,采用如下非线性函数学习住院费用与诊断数目的关系:
其中:A表示ADRG组别,Ci(A)表示在组别A中诊断数目为i项的住院费用预测值;aA(aA>0)是组别A的基准费用系数;bA(bA≥1)是变异系数,表示组别A中增加1个诊断后费用的相对变化;r(0 步骤2:基于迭代校正的诊断复杂程度DCL估计 根据住院费用与诊断数目关系模型计算诊断x在A中的相对费用C(x;A): 其中:Ei(x;A)表示A内含有诊断x且诊断数为i的病例集合;|Ei(x;A)|表示Ei(x;A)集合的病例总数;Ci(x;A)表示在组别A诊断数为i的病例中诊断x对住院费用变化的相对贡献, 这里c(p)是集合Ei(x;A)中某一病例p的住院费用. 据此,可计算每个诊断x的诊断复杂程度: 现进一步考虑诊断类型对住院费用的影响.定义Cost(p,x)为病例p在未增加诊断x前的预测费用: 其中:n表示病例p的诊断总数;di表示病例p除诊断x外其他诊断按照DCL降序排序后排名第i的诊断. 诊断x的相对费用C(x;A)可采用Cost(p,x)进行修正: 修正后的诊断x的相对费用贡献可用于再次计算该诊断的复杂程度DCL,而再次计算后的DCL又可进一步修正诊断x的相对费用贡献,此过程将不断迭代,直到迭代次数达到阈值上限I或者相邻两次迭代后的DCL差值小于阈值θ为止,即 DCLi(x;A)-DCLi-1(x;A)<θ 步骤3:病例临床复杂度评分ECCS计算 基于各诊断复杂程度DCL,采用原ECC模型中对病例临床复杂度评分的计算公式,可得病例p的临床复杂度评分ECCS.ECCS的计算公式如下: 为验证本文所提方法的有效性,本文基于真实病案首页数据,将本文所提改进模型与经典ECC模型进行对比实验.验证方式是分别基于两个模型得到的住院病例预测费用与实际费用进行Pearson相关性分析[7],如果相关性越高,说明某个模型所构建的病例复杂程度评分越能够反映资源消耗程度. 本文使用的数据来自重庆某大型三甲医院.该数据集包含2015-2019年该医院呼吸系统和循环系统的病案首页数据,经过异常数据剔除等数据预处理后,共获得呼吸系统13个ADRG组(后文用E1-E13标识呼吸系统ADRG组类别)数据38 003条,循环系统19个ADRG组(后文用F1-F19标识循环系统ADRG组类别)数据66 482条.本文所用数据集的基本统计特征见图1和图2.如图1所示,大多数的病例同时存在多种诊断类型.如图2所示,同一大类疾病的每个ADRG组之间,其诊断类型数目存在较大差异. 图1 数据集中病例数与诊断数目分布情况 图2 数据集中各ADRG组别的诊断类型数差异 基于IECC模型和ECC模型的预测费用与实际费用的相关性分析结果如表1所示.结果表明,IECC模型预测费用与实际费用相关性在除“其他呼吸系统疾患”以外的所有ADRG组别都有不同程度的提升,这说明基于迭代校正思想同时考虑诊断类型和数目的IECC模型能够基于高维稀疏病例数据更好提取病例诊断复杂程度. 表1 IECC模型与ECC模型的对比分析结果 本文以住院病人诊治复杂程度估计为应用背景,提出了一种针对高维稀疏数据、基于迭代校正思想的特征提取方法.基于真实病案首页数据的对比验证实验表明,基于IECC模型所预测的住院费用与真实费用的相关性与ECC模型相比有明显提升,说明基于IECC模型提取的病例临床复杂度评分这一新特征能够更好地反映病例资源消耗程度,即本文所提模型具有有效性.本文所提IECC方法可为DRGs的成功实施提供有力支持,还可广泛应用于考虑资源消耗的手术术式度量等众多应用问题,具有较大的现实应用价值.3 实验及结果
3.1 数据集
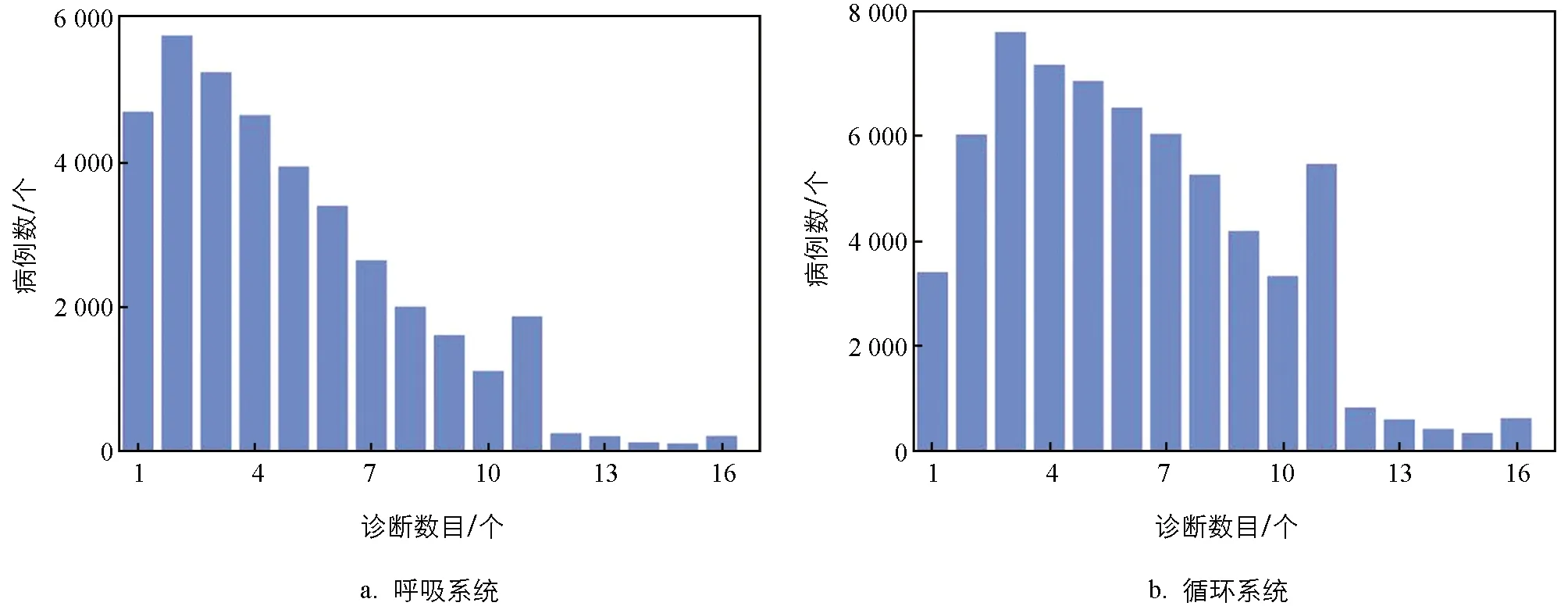
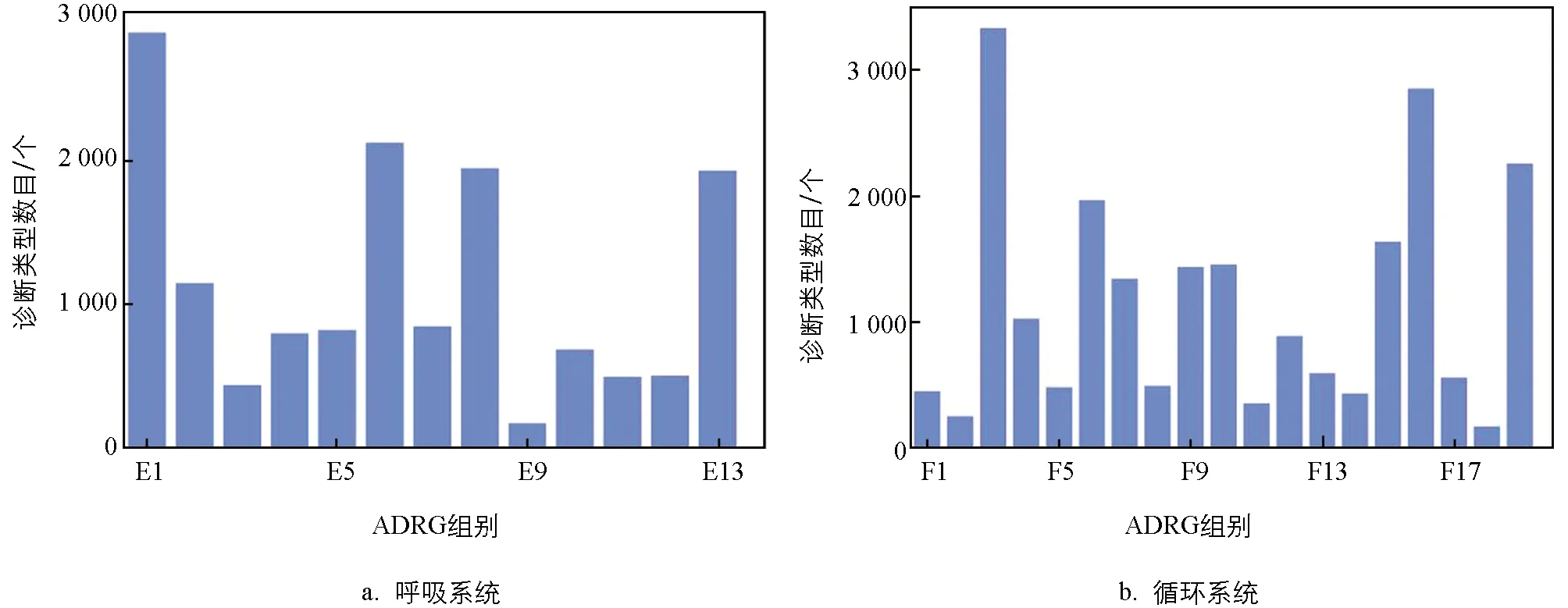
3.2 实验结果
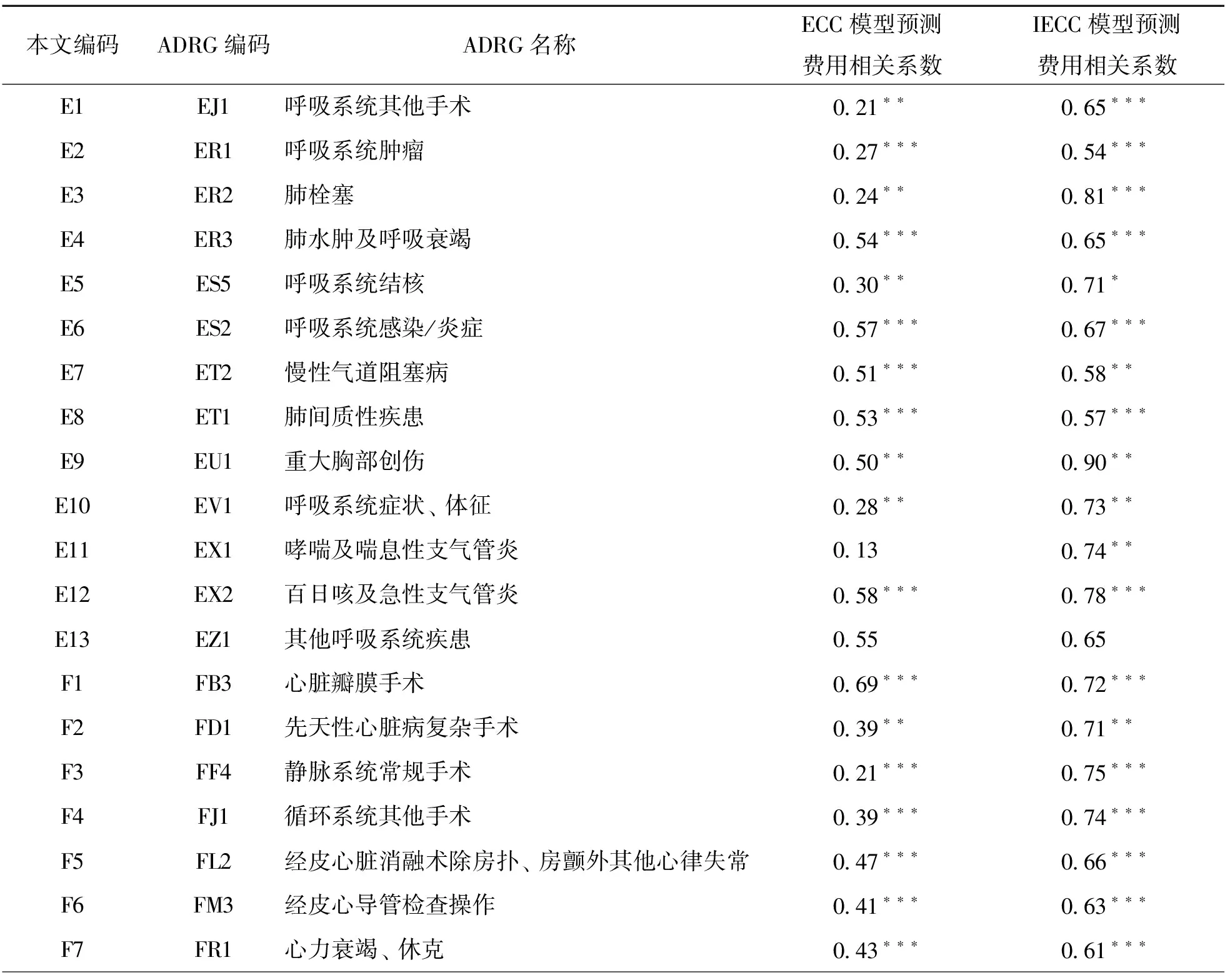
4 总结

