基于割点的社交网络影响最大化问题

杨书新，宋建缤，梁 文

1.江西理工大学信息工程学院，江西赣州 341000

2.长春理工大学计算机科学技术学院，长春 130000

近年来，信息技术的飞速发展带动了社交网络服务业的发展，如Facebook、Twitter、新浪微博和豆瓣等。We Are Social 和Hootsuite 在《2020 全球数字报告》中指出，普通网民平均每天要花费大约7 h 在社交网络上，社交媒体用户数更是突破38 亿。而微信这一个社交平台，全球每月就有11.5 亿用户使用它进行交互，产生了大量的信息。这些信息传播的速度之快、范围之广，使得社交网络上信息传播问题越来越受到学者们的关注。社交网络影响最大化问题作为信息传播问题中的一个重要问题，它蕴含着巨大的商业价值，如个性营销、谣言控制和链路预测等。

为了解决影响最大化问题，学者们给出了不少解决方案。现有方案主要分为贪心式和启发式两大类。贪心式虽然拥有精度保证，但较低的时间效率使这类算法难以应用于大规模网络。相比贪心式，启发式可以有效地解决时间效率低的问题，但现有的启发式算法对网络特征的挖掘不够充分，没有结合节点特征和结构特征看待影响最大化问题。面临时间效率低和网络特征挖掘不够充分的两大问题，本文综合考虑节点特征和社交网络拓扑结构，提出了CVIM（cut-vertex-based influence maximization）启发式算法。本文的主要贡献：（1）将割点相关理论应用到信息传播问题中，提出了基于割点的影响最大化算法CVIM；（2）在四个开源数据集上验证了CVIM 算法在社交网络上的实用性和有效性；（3）对CVIM 算法在社交网络上多方面的表现进行了分析。

1 相关工作

影响最大化问题进入学术界是在2001 年，Domingos 和Richardson提出用马尔科夫随机场来模拟信息传播过程，并给出了一个启发式的解决方案，给学者们打开了一道新的大门。紧接着，在2003 年，Kempe 等人将影响最大化问题定义为一种top-的离散最优化问题，即找出影响传播范围最大的个种子节点。此外，他们还提出了两种基本的传播模型，线性阈值模型和独立级联模型，并证明了在这两种传播模型下，影响最大化问题是一个NP 难问题。他们提出了一个近似比为(1-1/e)的Greedy 算法，可以得到影响最大化问题最优解63%的近似解。他们提出的这些方法和结论给影响最大化问题的研究奠定了基础。尽管Greedy 算法得到的近似解效果不错，但它的时间复杂度非常高。针对这一问题，学者们提出了一些降低时间复杂度、提高效率的方法。

根据影响最大化问题目标函数的子模性，Leskovec等人提出了CELF（cost-effective lazy-forward）算法。它的主要思想是：对于任意边=(,)，若节点在上一轮的边际收益小于等于节点的边际收益，则从当前轮开始，节点的边际收益不用计算。该算法比传统的贪心算法提高了近700 倍。为了进一步提高时间效率，Goyal 等人在CELF 算法的基础上提出了CELF++算法。与CELF 算法不同的是，CELF++算法先为任意节点记录了在当前迭代中边际收益最大的节点._，然后计算节点的边际收益。若._在当前迭代中选为种子节点，则在下一轮迭代中就不需要计算节点的边际收益。相较CELF 算法，CELF++算法节省了35%～55%的时间。

以上这些算法都是以贪心算法为基础提出的，因此都具有时间复杂度高的弊端。为了解决这一问题，学者们提出了基于启发式算法的一系列算法。Chen 等人提出的DegreeDiscount 算法，它的主要思想是：若节点的邻居节点中存在种子节点，那选择作为种子节点时，需要先将节点的度数进行定量打折，然后选度数最大的个节点。DegreeDiscount算法相比贪心算法提高了时间效率，但精度不高。因此，Chen等人基于节点局部区域的影响值近似估计全局影响值的思想，提出了PMIA（prefix excluding maximum influence arborescence）算法。它通过最大影响路径来构建最大影响子树（maximum influencearborescence，MIA），并通过调控子树的大小来达到时间效率和精度之间的平衡。尽管PMIA 算法在一定程度上平衡了时间效率和精度，但当网络图的密度较大时，会将影响限制在最大影响路径范围内，使得影响估计误差较大。根据面积密度公式，Ibnoulouafi 等人提出了节点密度中心性，并用节点密度中心性来度量节点的影响力。密度中心性考虑了节点的多层邻居的影响，因此比其他中心性的度量值更准确。但其本质仍然是用节点的度来计算密度，因此精度不是很高。

尽管贪心算法和启发式算法分别能得到较好的算法精度和时间效率，但它们都无法较好地平衡算法精度和时间效率。因此，曹玖新等人提出了一种综合启发式和贪心算法的MHG（mix heuristic and greedy）算法。它的核心思想是：先通过启发式算法选出候选种子节点集，再用贪心算法从候选种子节点集中筛选出种子节点集。MHG 算法的精度接近于贪心算法，并且时间效率要高于贪心算法，较好地平衡了算法精度和时间效率。但MHG 算法也同时拥有所选启发式算法和贪心算法的缺陷。如Cao 等人选择的PMIA 算法在图密度大时影响度量不准确，以及他们没有考虑边际收益问题。

为了得到好的算法精度和时间效率，学者们不再仅仅考虑节点的单一环境因素和单一特征。Zareie等人提出度量节点的影响力需考虑直接影响、间接影响、直接覆盖、间接覆盖四因素，他们采用多目标决策分析中的TOPSIS（technique for order preference by similarity to an ideal solution）方法综合考虑这四个因素，并提出了MCIM（multi-criteria influence maximization）算法。虽然MCIM 算法不仅考虑了节点与邻居的直接与间接影响，而且考虑了不同节点的邻居覆盖问题，但是它仅仅考虑了节点的度这一单一特征。Yang 等人则利用多目标决策分析中的VIKOR（vlsekriterijumska optimizacija I kompromisno resenje）方法综合考虑了节点的度中心性、紧密中心性和介数中心性三种特征，并提出了EW-VIKOR（entropy weighting VIKOR）算法，但EW-VIKOR 算法的精度与单一特征相比提升并不明显。

鉴于已有的影响最大化算法大多数关注于节点的特征（如度、密度等），很少关注社交网络的结构特征（如连通分量、桥等）。因为割点连接着图中的连通分量，是图的重要组成部分。并且文献[16-17]都证实了割点在网络中扮演着重要角色，在网络的连通性方面起重要性作用，它们一旦失效或被移除，网络都将可能瘫痪。因此，本文综合考虑节点特征和社交网络结构特征，提出了一种基于割点的影响最大化算法CVIM。

2 相关概念及形式化描述

在现实生活中，往往存在着一些关键角色，虽然它们可能不是主角，但它们是整个拼图中必不可少的一块（如中介、经纪人、交通枢纽等）。把这些关键角色映射到网络图上，他们就是网络图中的割点。在给出割点的定义之前，必须先提一下连通图和连通分量的基本概念。因为割点是图中的一种特殊的点，它与图的连通性有关。本文通过图例介绍了连通性的相关概念，详细情况见图1。

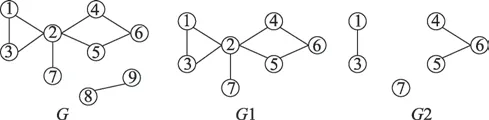
图1 图的连通性示例Fig.1 Example of graph connectivity

在图1 中，是一个无向图，同时也是非连通图。而1 是一个连通图，因为在1 中，任意两个不同的节点之间都存在可达路径。此外，1 是的子图，并且如果往1 中加上(8,9)这条边，1 就不是连通图。基于这些前提，则可以推断1 是的极大连通子图，同时也可以称1 是的连通分量。因为连通图的极大连通子图就是它本身，所以1 也是1 的极大连通子图，即1 是1 的连通分量，并且是唯一连通分量。2 是将1 中的节点2 以及与节点2 相关联的边删除后得到的无向图。从图中可以看出，2有3 个连通分量，1 只有1 个连通分量，去除节点2以及与节点2 相关联的边使得图的连通分量增加，满足这个条件的节点被称为割点，即节点2 是1 的割点。割点的定义如定义1 所示。

（割点）假设=(,)是无向连通图，若存在′⊂，且′≠∅，将′中的节点和与这些节点相关联的边都从中删除，可以得到两个或两个以上的连通分量，则称′为的点割集。若′={}，则称是连通图的割点。

给定一个无向连通图=(,)，对任意节点∈都满足C=(-{})-()，且C≥0。

其中C是节点对应的连通分量增加数，-{}是从图中去除节点以及它相关联的边后得到的图，(-{}) 是图-{} 中的连通分量数。如果C＞0，则节点是割点。在图1 中＞0，因此节点2 是割点，它连接着3 个连通分量。在信息传播过程中，一旦节点2 被阻塞，3 个连通分量之间就无法传递信息。但如果从节点2 开始传递信息，3 个连通分量都可达，传播范围变广。本文分别选取度数高的节点和割点进行信息传播对比，如图2 所示。

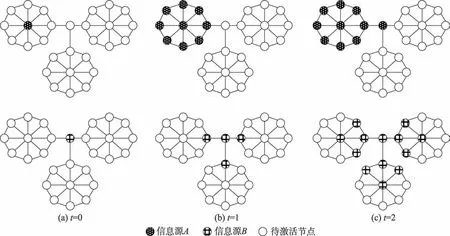
图2 信息传播对比（假设传播概率为1）Fig.2 Comparison of information spreading(Suppose probability of propagation is 1)

在图2 中，信息源是度最高的节点，信息源是割点。子图（a）～（c）分别是信息源和信息源在=0、1、2 时的传播状态图。很显然，信息源虽然在传播前期因为邻居节点多而占据优势，但是到了=2 时，信息源因为它所处的关键位置而比信息源传播得更广。因此，割点作为种子节点是可行的。但是在实际网络中存在的割点也不占少数，尤其是大规模网络。因此本文提出用割点所对应的连通分量增加数来度量节点的影响力，并且综合考虑节点的特征与网络的结构特征。种子集的求解式如式（1）所示：

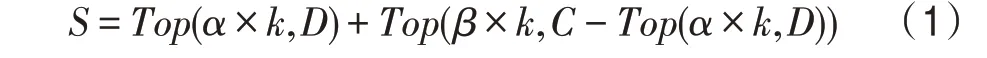
式（1）中，是大小为的种子集，和是调节参数，其中+=1。和分别是以度值和连通分量增加数筛选出的候选种子集。(×,)表示从候选种子集中选出前×个种子，-(×,)是候选种子集与前×个种子集合的差集，防止最终筛选出的种子出现重复。

3 CVIM 算法

为了解决影响最大化问题，本文提出先计算网络图=(,)中节点对应的连通分量增加数，然后根据节点度数排序挑选出影响力最大的×个种子节点，根据节点对应的连通分量增加数排序挑选出除之前挑选出的种子之外的×个种子节点。CVIM算法的流程图如图3 所示。

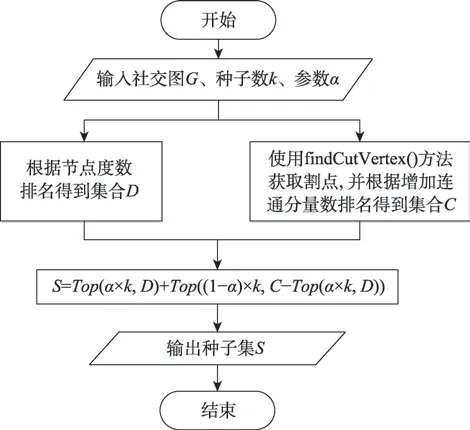
图3 CVIM 流程图Fig.3 Flow chart of CVIM

传统的求解割点的算法是删除一个节点，然后使用DFS 算法遍历图，如果图的连通分量增加，则删除的节点是割点。这种求解割点的算法需要使用||次DFS 算法，而本文使用的算法仅仅需要将所有的节点和边访问一次即可，即时间复杂度仅为(||+||)就能找出图中所有的割点，并求出其所对应的连通分量增加数。图4 是一个割点求解实例。

图4（b）所示为从节点出发深度优先搜索遍历子图（a）所得的深度优先生成树。子图（b）中的实线代表树边，虚线代表回边（即不在生成树上的边）。观察深度优先生成树的结构，可以发现有两类节点可以成为割点。这两类节点的具体情况如下：

图4 割点求解实例Fig.4 Instance of getting cut-vertex

（1）对于根节点，若它有两棵或两棵以上的子树，则该根节点是割点。因为深度优先生成树中不存在连接不同子树中顶点的边，所以，如果删除根节点，生成树变成森林。

（2）对于分支节点（即非根节点，也非叶子节点），若它的子树的节点都没有指向节点的祖先节点的回边，则节点是割点。因为如果删除节点，它的子树和生成树的其他部分将不再连通。

对于根节点，可以直接判断它的孩子节点个数，处理十分简单。但是对于非根节点，判断节点之间是否有回边就显得有些困难。本文采用[]和[]分别记录节点在深度优先遍历过程中被遍历到的次序和记录节点或它的子树追溯到最早的祖先节点的次序。这样，只需将所有的节点和边遍历一次，就可以更新所有节点的和值。这两个值的计算公式如式（2）所示：

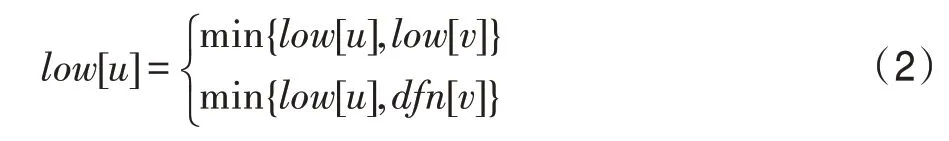
式（2）分为两种情况：（1）(,)是树边；（2）(,)是回边，并且不是的父亲节点。根据式（2），得到图3（a）节点∈{,,…,}对应的[]和[]值，详细数据如表1 所示。

表1 图3（a）中各节点对应的dfn 和low 值Table 1 dfn and low of nodes in Fig.3(a)

得到节点∈{,,…,}的[]和[]值之后，本文根据这两个值的关系判别节点是否为割点。判别节点是割点的条件如下所示：

（1）节点是根节点，并且有两个或两个以上的孩子节点；

（2）节点不是根节点，但对于(,)满足[]≥[]。

根据第3章中对割点相关概念的介绍，再加上图4的求解割点过程，下面给出割点以及其对应的连通分量数的求解算法()。

(,)

其中，第1～4 行是初始化阶段，初始化一个空栈，次序标记和子树数量，以及节点对应的连通分量增加数[]，并为节点设置[]和[]初值，然后将节点放入栈中。第5～17 行是迭代阶段，更新节点的[]和[]值。其中第9～15 行是当(,) 为树边时，先递增子树数量，然后递归求出[]用来更新[]的值。若节点是根节点并有两个或两个以上的子树时，节点对应的连通分量增加数量加1；若节点不是根节点但[]≥[]时，节点对应的连通分量增加数量也加1。第16～18 行是(,)为回边时的情况，最后返回[]。根据表1 和算法1，可以得出图1 中的割点为，并且对应的连通分量增加数为2。

算法1 获得了割点以及它所对应的连通分量增加数。基于此，本文给出求解种子集的算法CVIM。

(,,)

算法CVIM 中，第1 行先初始化种子集。第2～5行，根据节点的度排序，获取前×个种子节点。第6～12 行，先根据算法1 获取节点所对应的连通分量增加数，再根据它排序，获取剩下的-×个种子节点。最后返回种子集。

在算法1 中，找出连通图中的割点并记录它所对应的连通分量增加数的时间复杂度仅为(||+||)，而在算法2 中，获取节点度排序的时间复杂度为(||)，获取所有节点对应的连通分量增加数的时间复杂度为(||×(||+||))，因此，综合两个算法的时间复杂度为(||×(||+||))。

4 仿真实验

为了验证CVIM 算法求解影响最大化问题的有效性，本文在4 个真实的开源网络数据集上进行了仿真实验，这4 个网络数据集都下载自开源网站http://networkrepository.com。其中数据集anybeat 是从在线社交平台anybeat 上收集到的用户关系网络，数据集brightkite 是从基于位置的网络服务网站的开源API 获取到的友谊网络，数据集epinions 是从在线社交网站epinions 上获取到的信任关系网，数据集HepPh 是来自Arxiv 网站上的高能物理合作网络。数据集的基本信息如表2 所示。

本文实验采用传染病模型进行信息传播模拟，其中感染概率为0.1，恢复率为网络平均度的倒数，传播步长为网络直径（网络直径是网络的平均路径长度，代表了网络的一定特征。将传播步长设置为网络直径更贴近现实生活中的信息传播）。感染率和恢复率的取值都是基于传染病模型的信息传播仿真实验的常见取值，见文献[14]和文献[18]。

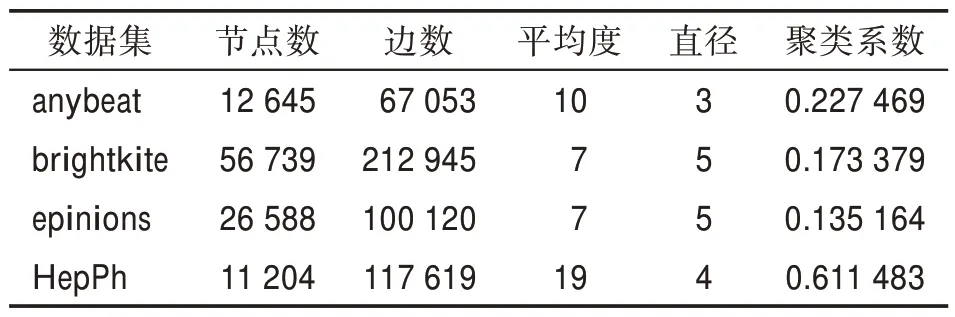
表2 实验数据集的基本信息Table 2 Basic information about experimental datasets

由于CVIM 算法是根据式（1）来选择种子节点，需要先确定式（1）中的参数和，然后才能从候选种子集和中筛选出种子节点。本文设计了实验来确定这两个参数，由于+=1，只要确定其中一个参数，另一个便可得知。因此，本文通过信息传播模拟，根据参数在不同取值时，获取到的种子节点的激活节点数来评估参数的优劣，实验结果见图5。

在图5 中，横坐标是参数的取值，纵坐标是种子节点最终激活节点数（即影响传播范围）。此外，本文考虑到种子集大小对结果的影响，还对比了在取不同值的情况下，参数对应的激活节点数的变化。根据图5 的实验结果，可以看出小于40 时，激活节点数大体呈上升趋势，因为种子集小时，度更能充分发挥它的前期优势；而当大于40 时，激活节点数先呈上升趋势，在参数=0.5 时，激活节点数达到峰值，取值大于0.5 时开始呈下降趋势，因为此时割点占据主导地位。这也印证了图2 表现出的现象。对于数据集anybeat 出现上升、下降、上升的趋势，是因为取值从0.5 到0.6 时，从anybeat数据集挖掘的种子节点间影响力重叠增加量最多（见表3，设置为100，以=0.1 时的种子间边条数为基准），导致激活节点数急剧下降，之后得到缓解，从而又开始上升，这是数据集的特殊性。而数据集brightkite 大体出现上升趋势，只有=100 这条曲线有上升、下降的趋势，这是因为该数据集的规模相对较大，而种子集大小就显得较小，从而激活节点数的峰值点滞后。数据集epinions 也出现了轻微的滞后现象，而数据集规模相对较小的HepPh 则没有出现滞后现象。综合4 个数据集的模拟结果，本文将参数设置为0.5，即参数也为0.5。

图5 参数α 对比Fig.5 Comparison of parameter α

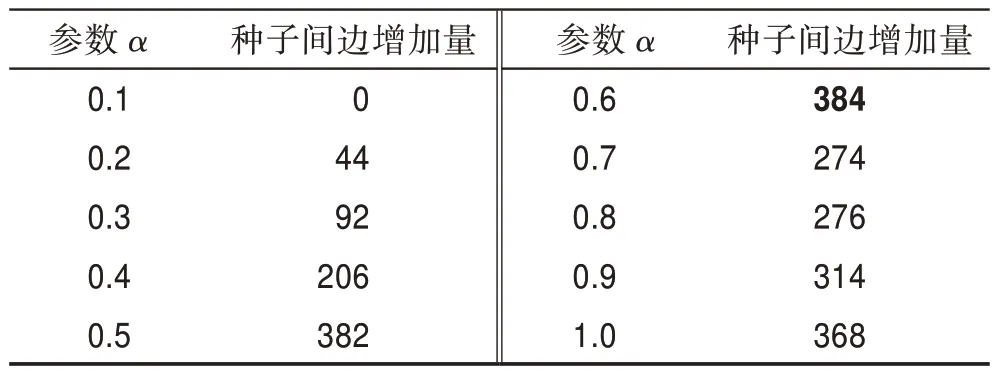
表3 anybeat数据集影响力重叠分析Table 3 Influence overlap analysis of anybeat dataset

参数取值确定之后，根据参数从候选种子集中获取了种子节点。为了验证CVIM 算法挖掘种子的实用性和有效性，本文分别根据算法运行时间和种子影响传播范围两个指标设计了算法对比实验。算法运行时间即指算法挖掘种子所花费的时间，种子影响传播范围则指用算法挖掘出的种子节点进行信息传播模拟，得到的激活节点数。算法运行时间对比实验中，种子数设置为100。参与对比的算法有：紧密中心性（closeness centrality，CC）、度中心性（degree centrality，DC）、密度（density）和混合多种影响因素的MCIM 算法。实验结果如图6 和图7 所示。

在图6 中，横坐标为5 种算法，纵坐标是各个算法挖掘100 个种子节点所耗的时间。从图6 可以看出，算法CC 挖掘种子所耗时间最长，这是因为算法CC 挖掘种子过程中需要反复地遍历路径，十分耗时，这一特点在网络直径较大的数据集brightkite 和epinions 上特别明显。算法DC 挖掘种子所耗时间最短，本文所提算法CVIM 与算法DC 基本持平，差距仅在0.3 s 以内。因为算法DC 仅需要统计节点邻居个数，极少时间内就能完成。算法CVIM 除了需要统计节点邻居个数之外，还要统计节点对应的连通分量增加数，因此比算法DC 多花了些时间。算法Density 虽然也是统计节点邻居个数，但它需要统计3级邻居，因此花费时间比算法DC 和算法CVIM 多。相比算法Density，算法MCIM 仅考虑了2 级邻居，在稀疏的社交网络上，去重操作花费时间并不多，因此一般情况下的运行时间比算法Density 少。但在聚类系数较高的数据集HepPh 上，算法MCIM 的去重操作需要花费不少时间，因此运行时间比算法Density长一些。算法CVIM 在4 个数据集上的运行速度比算法CC、Density 和MCIM 平均快9 089 倍、790 倍和280 倍。从图6 中的整体表现可以看出，算法CVIM拥有很高的时间效率，因此它在运行时间指标上具有一定的优势，更适用于大规模网络。

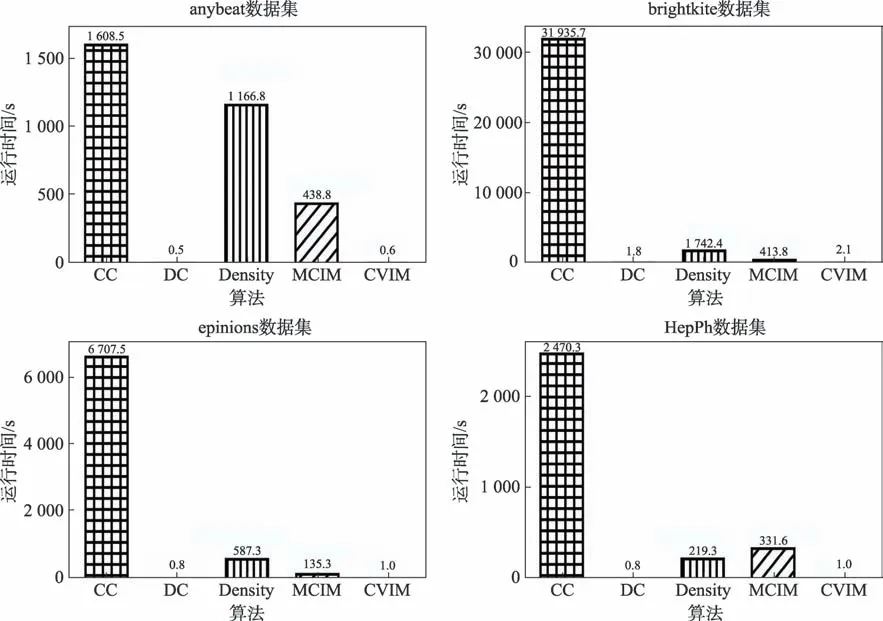
图6 运行时间对比Fig.6 Comparison of running time

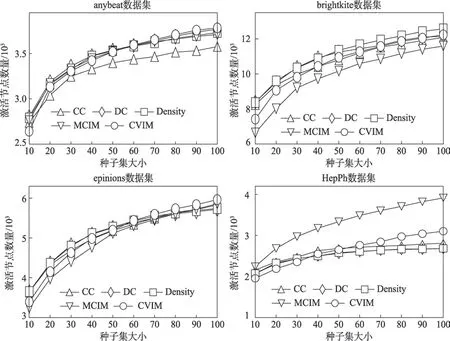
图7 影响传播范围对比Fig.7 Comparison of influence spreading

在图7 中，横坐标为种子集大小，纵坐标为激活节点数量，5 条曲线分别对应CC、DC、Density、MCIM和CVIM 五种算法。在4 个数据集中，种子集较小时，CVIM 算法处于劣势，但当种子集逐渐变大时，CVIM 算法也逐渐接近其他算法，尤其是在数据集anybeat和epinions 中后来者居上，占据优势地位。在数据集brightkite 和epinions 中，算法MCIM 表现一般，是因为这两个数据集的聚类系数相对较小，而在聚类系数较大的HepPh 中，表现突出（见表2）。算法CC 是根据路径长度度量节点的影响力，因此在网络直径较小的数据集anybeat 上，节点影响力的区分度比较低，筛选出的种子节点的传播效果较差。算法DC 和Density 都是根据节点的度评估节点影响力，不同点在于Density 将2 级和3 级邻居的度也作为评估因素，因此Density 比DC 占据微弱的优势。与算法DC 和Density 相比，算法CVIM 在种子集小时(＜50)效果一般，这是因为在种子集较小时，度占主导优势，但这种优势是短暂的，只有少数节点的度数特别大。在＞50 时，割点获取了主动权，实现反超。因为算法CVIM 考虑了网络的结构特性，使得算法CVIM 对网络的特征差异敏感度低，对网络的适配度较高。因此比算法MCIM 和CC 都稳定。综合4 个数据集上的实验结果来看，随种子集大小的增加，算法CVIM 对应种子的影响传播范围稳步扩大，受到其他因素的干扰较小，因此算法CVIM具有一定的优势。

为了进一步验证CVIM 算法的有效性，本文还设计了种子间紧密性实验，探究各算法所选种子是否存在“富人俱乐部”现象。“富人俱乐部”现象是复杂网络的一种结构属性，可以用来区分幂律拓扑。它表现为“富人”节点之间的连通性远远高于其他节点。即“富人”节点之间紧密性远远高于其他节点。本实验中的“富人”节点即指种子节点。该实验的设计思路：首先读取社交图，再读取各算法选出的种子节点，匹配种子节点间边的条数，若边的条数越多，说明种子间的紧密性越高，它们的影响力重叠量越大，“富人俱乐部”现象越明显。实验设置种子集大小为100，实验结果如图8 所示。

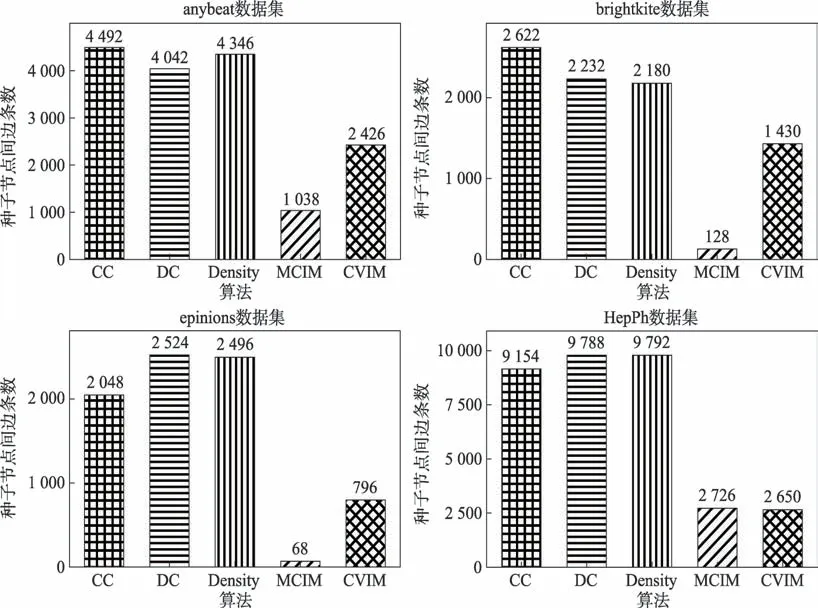
图8 种子富集性对比Fig.8 Comparison of seed enrichment

在图8 中，横坐标是五种算法，纵坐标是算法挖掘出的种子之间的连边条数。在4 个数据集中，算法CC、DC 和Density 挖掘出的种子，它们的紧密性偏高，进一步解释了图7 中这三种算法的表现一般的结果。算法CC 的种子富集性比算法CVIM 和MCIM 平均高2.4 倍和14.6 倍，算法DC 的种子富集性比算法CVIM 和MCIM 平均 高2.5 倍和15.5 倍，算法Density的种子富集性比算法CVIM 和MCIM 平均高2.5 倍和15.4 倍。算法MCIM 因为考虑了影响覆盖因素，所以种子间的紧密性较低。在数据集HepPh 中，算法MCIM 挖掘的种子紧密性高于CVIM 是因为该数据集的聚类系数明显比其他数据集高（见表2）。综合4个数据集上的表现，除去算法MCIM，CVIM 体现出了割点的优势，一定程度上消除了“富人俱乐部”现象。

5 结束语

由于割点在图论中扮演着不可或缺的角色，本文基于图论中的割点理论，提出了基于割点的影响最大化算法CVIM。它将连通分量纳入到评估节点影响力的指标中，并结合度的优势，筛选出了有效的种子集，从而求解了影响最大化问题。实验结果表明，CVIM 与部分具有代表性的算法相比，在影响传播范围和种子富集性指标上具有一定的优势，并且能有稳定的表现。但在现实生活中，挑选出的种子节点的影响力往往会因为时间、空间等因素而衰减，已有研究表明可以通过修改网络的结构，提升种子节点的影响力。因此，未来工作将从网络的结构出发，进一步分析如何减缓种子节点影响力的衰减或提升种子节点的影响力。