基本不等式教学中的几个问题情境

宁红国

（河北栾城中学，河北 石家庄 051430）

《普通高中数学课程标准（2017 年版）》要求要了解并会证明基本不等式；会用基本不等式解决最值问题。对于基本不等式的考查几乎每年高考都会涉及，难点在于变形化简构造成基本不等式的基本结构，还要注意“一正二定三相等”。对于基本不等式的证明，可以培养学生数形结合的数学思想。在应用的过程中，通过条件的转换和变式，培养学生形成类比归纳的思想和习惯，进而形成严谨的思维方式。

情境问题一：把一个物体放在天平的一个盘子上，在另一个盘子上放一砝码使天平平衡，称得物体的质量为a，由于天平不准确，天平的二臂长略有不同（其他因素不计），那么a 并非实际质量，不过，我们可作第二次测量，把物体调换到天平的另一个盘子上，此时称得物体的质量为b.那么物体的实际质量是多少呢？

情境问题二：某商场对商品价格进行了调整，有下面几种打折方式，问哪一种打折方式对顾客更有利：①先打8 折，再打4 折；②先打7折，再打5 折；③先打6 折，再打6 折；④先打a折，再打b 折；⑤先打折，再打折.引导学生分别计算打折数量：①0.8×0.4=0.32 ②0.7×0.5=0.35 ③0.6×0.6=0.36 ④打ab 折 ⑤打折，从中可以看出两次打折的数据差值越大，商品价格越低，顾客越有利.所以可猜想ab≤（）2，由于a≥0，b≥0，上式两边开方得（a≥0，b≥0），又体现基本不等式的应用.

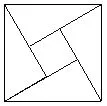
情境问题三：在一个正方形中，画出四个全等的直角三角形（如右图），其直角边分别为a、b，则四个三角形的面积和为2ab，正方形的边长为，由图形可得：四个三角形的面积和小于正方形的面积即2ab≤a2+b2，因为a≥0，b≥0，用去替换a、b，得出（a≥0，b≥0）.这种方法中体现换元法的应用.

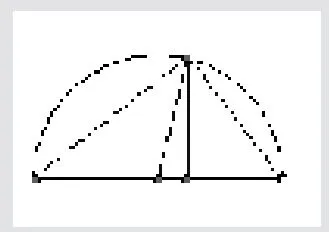
情境问题四：如右图，在一个半圆中，圆心为O，AC 为直径，B 是圆弧上一点，则∠ABC=90°，设AD=a、CD=b、BD=h 已知BD⊥AC，那么OB=，由垂线定理知h2=ab，由图形可知BD≤OB 即，从而得到基本不等式.

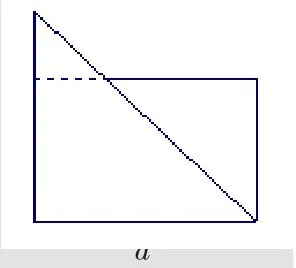
情境问题五：画出两个等腰三角形（如右图），直角边分别为a、b，且三角形的两腰重合，由图可知：两三角形的面积和大于以a、b 为边长的矩形的面积，即≥ab，然后同问题三的处理，可以看出当a、b 长度逐渐接近时，两图形面积逐渐接近，所以当a=b时取“=”，基本不等式成立.

基本不等式知识点作为高考中的重要考点,可以单独以填空选择形式考查,也可以与其他热门考点（三角，解析几何）结合以综合题形式进行考查,是求最值问题最有利的工具。因而，教学中要求学生正确应用基本不等式进行判断和计算，熟练掌握基本不等式的变形应用。我们在学习和教学的过程还是要重视基础，回归教材，突出双基。