一种基于模板匹配与隶属度解析的时序异常快速检测方法
龚汉鑫,齐金鹏,孔凡书,朱俊俊,曹一彤
(东华大学 信息科学与技术学院,上海 201620)
随着工业自动化、智慧医疗等行业的飞速发展,数据数量呈现出指数级的上升[1]。面向大规模时序数据的异常特征分析与快速检测技术在医疗等大数据领域的应用已成为热门研究方向[2]。传统的数据分析与检测技术需要读取整段原始数据样本,再进行后续的特征分析与统计量计算[3]。当面对数据量庞大且形式各异的异常数据时,传统方法的时间复杂度、检测精度等难以满足实际应用的需求[4]。目前,医疗病变数据分析采用常见的时域检测方法,主要在时域上简单分析病变数据的特征波形[5]。拟态法通过脑电信号波形的各种波形幅值、斜率和周期等参数[6]的差异来判定癫痫发作。该方法对于多种形态的医疗数据不敏感,准确率较低。类似于支持向量机(Support Vector Machines,SVM)的机器学习方法在数据分析中得到了广泛的研究,但该方法对于核函数选取主要依赖经验,SVM也不适用于将数据分成多类[7-8]。
时域分析方法对时序数据存在的局部信息不敏感[9],而支持向量机核函数选取依赖经验。针对上述问题,并为了满足大规模时序数据快速分析与异常状态检测等需求,本文提出了一种基于模板匹配与隶属度解析的时序异常快速检测方法。该方法首先采用滑动窗口理论[10]将待检测数据切分,实现对多突变点的时序数据特征提取,并探究最优的滑动窗口宽度W对检测精度的影响,以提高数据分析速度;然后,利用检测速度更快、准确度更高的TSTKS突变点检测算法[11],将多个连续窗口的波动量构建为波动向量。通过定义波动向量模板,并基于模板匹配[12]与隶属度解析[13]的方法实现对时序异常的特征分析与多异常状态的快速检测;最后,基于仿真训练集和测试集验证了本文所提方法的有效性,并基于脑电癫痫数据实现了数据异常的特征分析以及病变状态等快速检测等实验。实验结果表明,本文所提出的新方法能够通过对窗口的波动量进行标准化,提高算法的鲁棒性,可满足大规模数据不同病变状态的快速分析与检测等要求。
1 理论基础
1.1 概述
本文基于模板匹配与隶属度分析技术,提出了一种时序数据快速检测算法。如图1所示,该方法将TSTKS数据流突变点检测算法与滑动窗口理论相结合,在突变点检测基础上计算出窗口波动量;然后,根据多个连续波动量构建波动向量,提取整段数据特征。由于病变时序数据的波动向量与正常的波动向量有差别,故将待检测数据的波动向量中进行标准化,即归一化并二值化处理;最后,建立统一的基于病变信号波动向量标准模板集合,采用隶属度解析的方法,判断待检测波动向量与模板匹配的隶属度是否达到设定阈值,并由此判定待检测数据是否异常。

图1 基于模板匹配与隶属度解析的时序数据分析算法框架Figure 1. Framework of time series data analysis algorithm based on template matching and membership degree analysis
1.2 多突变点检测
本文针对大规模多突变点的时序数据,通过引入滑动窗口理论将其分成若干子段,然后采用TSTKS算法实现多突变点检测。时序数据是随着时间变化的数据,存在明显的时序性和彼此关联性,即任意t1和t2时刻的值是互不影响的,因此常被用于进行数据挖掘和突变点检测[14]。时序数据常见数学表达形式为
Z={x1,x2,…,xi,…,xn}
(1)
式中,xi代表某个数据流在i时刻对应的一个d维的数据向量;n为数据长度。当d取值为1,xi表示单变量;当d取值不为1,xi表示多变量。
采用基于元素个数的滑动窗口策略对时序数据Z切分,整段数据可被表示为
Sz={w1,…,wi,…,wk}
(2)
式中,wi=(xi+1,xi+2,…,xi+W);k代表整段时序数据滑动窗口的个数;W为滑动窗口内数据长度,可有效保证各个窗口数据量携带信息一致,以便更好地利用TSTKS算法进行数据异常检测。
1.3 归一化波动向量
本文利用滑动窗口切分整体待检测数据,并对各个分段数据分别应用TSTKS突变点检测算法。若在窗口中检测到数据突变点,则分别计算每个窗口内数据的波动量;若没有检测到突变点,则说明当前窗口数据波动量为零[15]。窗口波动量FW的定义为
(3)
式中,var(ZL)表示wi窗口内左半部分数据的方差;var(ZR)表示wi窗口内右半部分数据的方差;Z表示wi窗口内包含的全部时序数据;max(Z)和min(Z)分别表示时序数据的最大值和最小值。波动量不仅能够表示数据的波动特征,还可保留每个子段的信息。为了消除波动值之间数量级的差异,对波动量进行归一化处理[16],将所有特征统一到[0,1]区间。归一化计算式为
(4)
式中,FWmin为波动量序列中最小数;FWmax为波动量序列中最大数。然而时序数据具有复杂多变、海量的特点,单个窗口波动值无法快速获得数据的整体波动情况,不适合对大规模时序数据进行有价值信息的挖掘。因此,对于某段时序数据Z,应用TSTKS算法与滑动窗口理论得到每个窗口波动值,将m个连续固定宽度为W的窗口波动值NFi组成一个多维度的向量,称之为波动向量VN,如式(5)所示。
VN=[NF1,NF2,…,NFm]
(5)
波动向量的建立流程如图2所示。

图2 波动向量的构建Figure 2. Construction of wave vector
2 方法实现
本节围绕波动向量提出了基于模板匹配与隶属度解析的时序数据异常检测算法。通过与模板库中波动向量模板进行匹配分类,采用隶属度分析方法衡量模板匹配的相似程度,从而实现对数据快速检测分析。
2.1 基于模板匹配与隶属度解析的算法框架
在对时序病变数据构建波动向量的方法基础上,本文基于模板匹配与隶属度分析技术提出了一种时序数据异常检测算法。在已知数据特征或对应类别的前提下,在标准化波动向量的前提下预定义波动向量模板,建立波动向量模板库。通过时序病变数据反映的病情轻重缓急以及病变状态的不同,定义多个波动向量模板,例如针对病情是否发作可将正常状态的波动向量模板定义为[n1,n2,…,nm],而异常状态波动向量模板可被定义为[a1,a2,…,am]。
通过隶属度解析的方法对不同模板向量分别统计待检测向量各维度的隶属度。根据论域X为有限集时,记X={x1,x2,…xn},则X上的模糊集Ak可以表示为
(6)
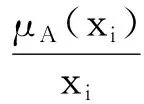
(7)
式中,σ为阈值。根据上述定义的波动向量VNWF,计算VNWF向量每个维度对应模糊集Ak的隶属度,然后通过比较不同的模板向量的隶属度值进行分析。
2.2 评价指标
为了对基于模板匹配与隶属度分析算法的性能进行评价,本文引用准确率(Acc)、查全率(Re)两个常用二分类问题指标作为评价指标。Acc是指对于给定的数据,匹配分类正确的样本数占总样本数的比例。Re指在所有的正类中被匹配为正类的比例。
(8)
(9)
式中,TP表示癫痫发作时正确匹配分类的样本数;TN表示癫痫未发作时正确分类的样本数;FP表示癫痫未发作被匹配成癫痫发作的样本数;FN表示癫痫发作被错误分成癫痫未发作的样本数。
3 方法验证
为了更好地说明基于模板匹配与隶属度解析算法对病变时序信号快速分析的优势,本文通过模拟时序数据采用不同宽度窗口,并根据波动向量模板与隶属度分析方法进行试验,以验证该方法的可行性。此外,本文选取实际脑癫痫数据进行多次实验,确定了最佳二值化阈值;设计并实现了基于脑电癫痫信号的病变特征分析,能够对不同病变状态进行检测。
3.1 仿真数据分析
当具有多突变点且时序数据长度n一定时,滑动窗口的宽度是关系突变点检测精度的一个重要参数。为进一步探究滑动窗口宽度W对突变点检测影响,多次对不同宽度W进行仿真实验。根据500次仿真结果,不同W下算法的检测指标如表1所示。

表1 窗口宽度变化500次突变点检测统计表
由表1可以看出,突变点检测的精度随着窗口W的增加呈现先增加后减小的趋势,这是由于当窗口宽度增大时,关键数据信息增加,检测精度提高。但当窗口过大时,窗口携带的信息过多导致数据分布差异被忽略,检测精度降低。时耗与窗口宽度大小呈现负相关关系,窗口越大,检测耗时越低。过大或过小的窗口都会导致突变点的漏检或误检,导致平均误差增大。
根据大多数病变特征信号相关概念可知,患者在未发病时的病变信号与正常人类似,其波动是比较平稳且有规律性的。在发病时,病变信号出现起伏剧烈,存在明显的波动,在疾病发作结束后到又逐渐恢复到正常波动。通过不同状态的模拟数据进行拟合,可在一定程度上表示真实时序病变数据,数据波动较大时代表异常状态。根据上述窗口试验,本文采用窗口宽度W为256进行突变点检测,其模拟时序数据检测效果如图3(a)所示。对模拟数据计算出的波动量进行归一化并二值化处理,预定义异常波动向量模板为[1,1,1,1]。采用模板匹配与隶属度分析的方法对模拟数据进行异常状态检测,其结果如图3(b)所示。
由图3可以看出,随着窗口更新,其异常概率增加,超出设定的0.5阈值警戒线,达到100%异常状态匹配概率。当时序数据在剧烈波动阶段时,异常状态匹配概率达到100%。剧烈波动结束后,异常状态的匹配概率随着窗口更新而降低并趋于0。该结果表明文中所提算法不仅能检测出时序数据的多突变点位置,其对时序数据异常状态的检测也有良好的效果。
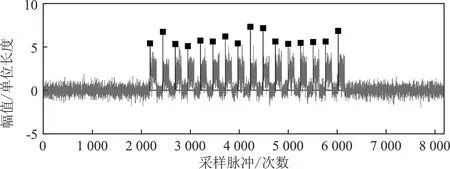
(a)
3.2 脑癫痫信号异常检测
为说明基于波动向量模板匹配与隶属度解析算法对病变信号检测性能,本文选取波士顿儿童医院癫痫数据库[17]进行实验。本文采用TSTKS算法与滑动窗口宽度W=256分别对正常脑电数据和癫痫异常脑电数据进行多突变点检测,结果如图4和图5所示。
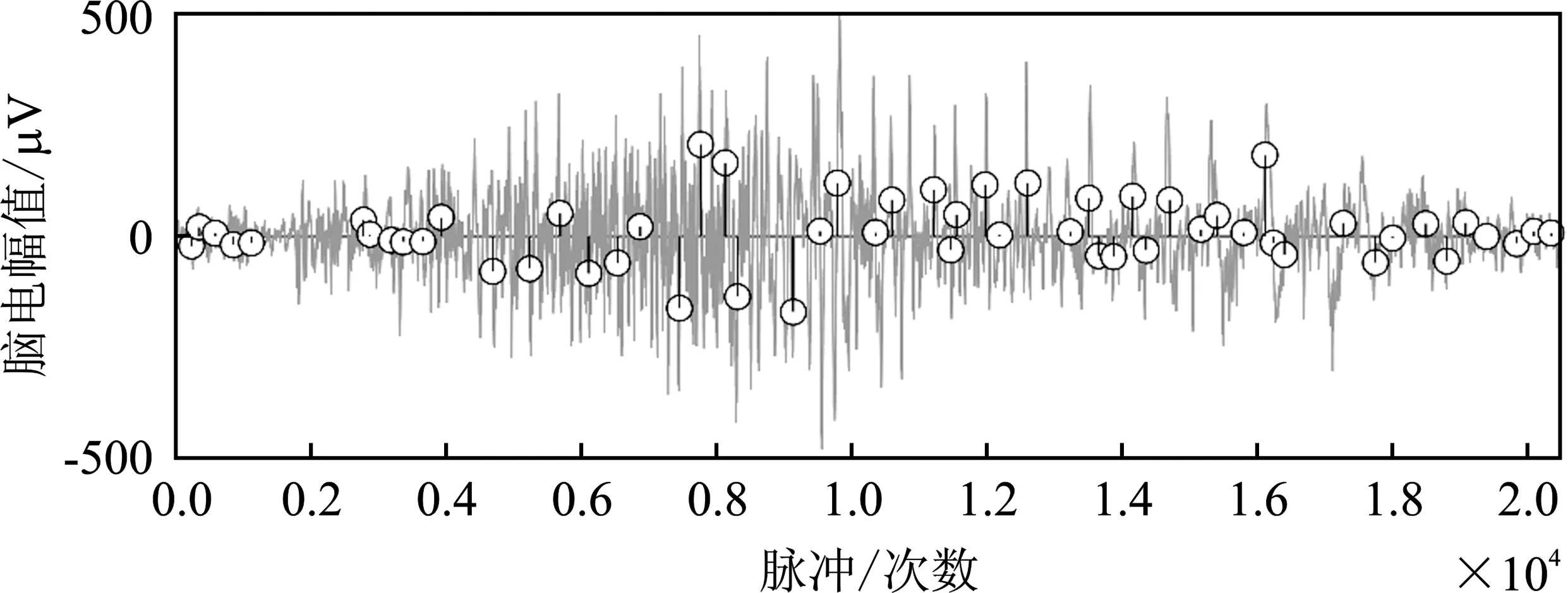
图4 癫痫发作时脑电数据突变点检测情况Figure 4. Detection of sudden mutation points in EEG data during epileptic seizure

图5 正常脑电数据突变点检测情况Figure 5. Detection of mutation points in normal EEG data
根据图4和图5的脑电信号对比可知,在未发病时,癫痫患者脑电信号与正常人类似,其波动是比较平稳且有规律性的。在发病时,癫痫患者脑电信号出现剧烈起伏。当癫痫发作结束,癫痫患者脑电波又逐渐恢复到正常。因此,采用滑动窗口与TSTKS算法对待检测脑电信号数据进行突变点检测,计算波动值并归一化,通过对归一化的波动值进行“好与坏”的分类,即将波动值进行二值化,忽略其数值的大小变化。根据对脑电数据的多次实验,本文拟定二值化阈值σ为0.185,将大于阈值的波动值映射为1,而小于或等于阈值的波动值映射为0。本文根据癫痫病变数据多次实验,选取连续4个窗口的波动值构建波动向量,定义正常脑电信号波动向量模板为[0,0,0,0],癫痫剧烈发作时模板为[1,1,1,1],并采用基于模板匹配与隶属度解析方法对脑电病变异常时序数据进行快速检测和诊断。波动向量模板匹配与隶属度解析结果如图6所示。
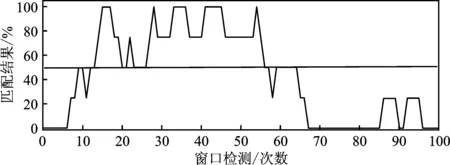
(a)
如图6(a)所示,第6次到第15次癫痫波动向量异常模板匹配结果呈现不断上升的过程,并超出警戒值0.5,表明处于癫痫发作的预警状态。在第15次到55次模板匹配时,匹配率基本处于75%以上,该实验结果表明在图4中,第3 000 s到3 040 s的癫痫病变脑电信号发生了剧烈波动。第55次到60次异常模板匹配的数值自50%逐渐下降,说明癫痫正处于发病结束阶段。由于还存在少部分痉挛,因此仍有脑电信号异常,导致第60次到第65次异常匹配结果为50%。而在癫痫发作结束后,第65次到95次异常模板向量匹配结果基本为0。第90次左右少数检测匹配率为25%,这可能是由病人活动如睁眼、脸部动作导致的神经信号变化。癫痫患者在发病时会有间歇性波动和眼部干扰,导致波动值较低,在总体数据检测过程中命中率会有一些波动,但通过对整体数据的匹配分析,本文提出的方法依然能够快速检测出患者是否处于发病状态。
为了说明该方法的性能和有效性,本文选取传统的相关系数模板匹配方法[18]和基于Manhattan距离模板匹配方法[19]进行对比验证,其实验结果统计如表2所示。

表2 3种模板匹配算法500次检测结果统计
由表2的平均指标结果表明,3种模板匹配方法都能够检测出癫痫异常状态,但基于隶属度分析的模板匹配方法在检测癫痫发作异常病变状态时更加有效。尽管该算法的时耗略高于Manhattan距离法,但是其在匹配准确率和查全率上都有更好的效果,说明该方法具有较好的检测性能。
4 结束语
本文基于模板匹配与隶属度解析技术提出了一种时序数据的特征分析与异常状态的快速检测方法。该方法采用滑动窗口理论实现时序数据分段与特征提取;采用TSTKS算法检测连续窗口的突变点,进而计算波动量的方式构建波动向量,并通过预定义的模板匹配与隶属度解析的方法实现数据异常的特征分析以及异常病变状态的快速检测。仿真数据和脑癫痫信号分析实验表明,本文所提方法是对原始数据的波动量进行分析,并将其二值化,实现了大规模时序数据分析方法的快速性、准确性和鲁棒性,能够满足大规模数据不同病变状态的快速分析与检测。

