基于Python语言的瑞利面波频散反演实行方案

吴为治，娄利，王鹏，王宾

(安徽省勘查技术院，安徽 合肥 230041)

0 引言

Python语言作为一种解释型的高级语言，其语法简单、代码可读性较高且易扩展移植，近年来迅速发展成为科学、工程研究领域内流行的编程语言。Python语言还具有功能强大且开源标准函数库以及第三方函数库，众多科学计算软件都提供有Python的安装调用接口，Github网站也提供Python软件包的开源以方便开发者搭建展开研究工作的平台。正是这样，调用高效完善的函数库，既能满足专业化研究的需求，又能进一步提高开发效率。彭一波等[1]提出利用Python 语言地震学数据处理软件包obspy进行背景噪声研究的工作方案，实现了两个地震台站之间噪声互相关格林函数波频散曲线的提取，并进行背景噪声源的时空性研究。这是利用Python语言建立地球物理研究平台一次成功的案例，然而其并未进行进一步频散反演。我们知道面波频散曲线含有丰富的地下层状结构信息,尤其对横波速度结构特别敏感，所以通过对频散曲线的反演可以得到地下层状介质的物理性质[2]。因此基于Python语言的频散反演方法的研究很有必要，可以为今后继续研究背景噪声成像、面波勘探提供开源的支持。

1 研究基础

1.1 频散正演算法

频散曲线的反演基于正演算法，面波频散的正演计算方法众多，如Knopoff算法[3]，广义反射—透射系数法[4]等，均能快速准确地求取面波频散。Python语言第三方函数库提供有disba软件包(https://pypi.org/project/disba)用于计算频散，该软件包使用Dunkin矩阵或者快速增量矩阵算法计算瑞利波相和群速度频散曲线；使用Thomson-Haskell方法计算勒夫波相和群速度频散曲线。GitHub上则有提供pysurf96软件包(https://github.com/miili/pysurf96)用来计算频散，其算法基于圣路易斯大学的CPS(computer programs in seismology)中surf96程序[5]，虽然需要Fortran编译环境，但稳定性更好。这里我们选择用pysurf96程序来测试(附录示例1)，选取一个简单的两层模型(表1)来正演瑞利面波的频散曲线(图1)。

表1 两层层状介质模型参数

图1 基于pysurf96计算的两层层状介质模型的瑞利面波频散曲线Fig.1 Rayleigh wave dispersion curve of two layered media model based on pysurf96

从图1中可以看出基阶瑞利面波相速度在低频部分接近模型半空间横波速度的0.9倍左右，高频部分接近模型上层横波速度的0.9倍左右；二阶面波相速度在高频部分趋近模型半空间横波速度；三阶面波相速度则在低频接近模型上层的横波速度。这与夏江海在《高频面波方法》中提到的现象一致[2]。同时，我们在测试不同速度模型中发现当地层模型中半空间的波速过低时，会无法得到某些频率的瑞利面波相速度，如使用软件包中surf96函数计算频散会报错，使用surfdisp96函数则需要先定义返回值为复数。这是因为频散方程在这些频率的根是复数，这里可以采用在原半空间的下方加上一层速度更高的层作为新半空间来计算频散。但这样会带来一定的误差[6]，最好是取频散方程复数根解的实部作为相速度来解决这一问题[7]。

1.2 频散反演理论和算法

频散曲线的反演是通过某种方式调节模型参数达到对实际频散曲线的最好拟合。这里我们构造目标函数:

Φ(m)=‖d-d(m)‖2,

(1)

即实际频散相速度d与速度结构模型m正演得到频散相速度d(m)的L2范数,来定义理论计算数据对实际数据的拟合程度。反演的过程实际上就是采用算法搜索调整m,使得目标函数Φ(m)为极小的过程,若m有多个,则取其目标函数值最小的那一个作为反演的最终结果。最初频散曲线反演方法主要利用半波长法、拐点法、渐进线法等。随着计算能力的进步，算法的开发，越来越多反演方法应用到频散反演中，尤其是启发式算法的出现，让反演效率和速度提升到一个新高度：凡友华等[8]使用的BFGS拟牛顿法引入到频散曲线的反演当中,提出了基于基阶模的拟牛顿法反演,在理论上进行了反演模拟;石耀霖等[9]以勒夫波为例讨论从面波频散反演地球内部构造的遗传算法;翟佳羽等[10]在蚁群算法引入集中度的概念并对层状介质模型以及实测数据的频散曲线进行反演,验证了方法的有效性。这些频散反演的方法大致可以分为以微分为基础的方法、枚举算法和随机算法。前面提到的BFGS拟牛顿法即利用了目标函数的一阶导数信息，应用于频散反演这种非线性化反演时,依赖初始模型的选择,容易出现不收敛的现象。遗传算法属于全局搜索方法，容易陷入局部极小值中,且反演用时较长、效率较低，但可进行优化。模拟退火法则是一种伪随机算法，通过用温度代表概率进行演算来搜寻最优解，更依赖初始模型和参数选择。

郭飞在Github上提供的scikit-opt(https://github.com/guofei9987/scikit-opt)软件包封装了多种启发式算法函数，并且在软件包的网络在线说明文档(https://scikit-opt.github.io/scikit-opt/#/zh/README)中给出了算法特性、详细的参数说明和使用案例。通过对提供的算法函数分析，其中可用于频散反演的有：遗传算法、差分进化算法、粒子群算法和模拟退火法。

2 算法设计和模型测试

首先需要实现频散正演的子程序，输入速度模型和需要计算的周期数数组，调用pysurf96程序包函数进行正演计算：如使用的是surf96函数，则要在模型下方增加一个更高速的半空间进行计算；如使用的是surfdisp96函数，则要取返回值的实数部分。然后实现输入不同模型时计算目标函数的子程序，最后在主程序实现文件数据的读写、参数的设定和反演算法的运算。其中，Python的numpy扩展库提供丰富的数组计算函数，为我们计算提供了方便，代码也显得更加简洁。例如在计算目标函数时需要进行L2范数运算，python语言可以用numpy.linalg.norm()方便快捷算出，省去了复杂数组计算的代码(附录示例2)。

a—差分进化算法;b—遗传算法;c—粒子群算法;d—模拟退火算法a—differential evolution algorithm;b—genetic algorithm;c—particle swarm optimization;d—simulated annealing algorithm图2 不同启发式算法反演的结果Fig.2 Results of different heuristic algorithms

可以看出深度越浅，横波速度结构反演的精度越高，例如图2a差分进化算法左图第一、二、三层反演的效果都很好，且无论是高速层还是低速层，都很好地反演出来。这是因为瑞利面波高频对浅层敏感；最后一层即半空间层的横波速度也都反演的较好。图2a右图则是反演得到模型的频散与实际频散曲线的差别，可以看出拟合很好。至于中间两层误差较大，我们可以利用disba软件计算瑞利面波的相速度敏感核进行探讨，图3是频率为2 Hz的瑞利面波相速度敏感核。从图中红线和黄线可以看出，纵波速度和密度的改变总体都对相速度影响很小；绿线的变化说明横波速度在0～20 m浅层变化对相速度影响大，30～50 m范围影响则较小，半空间层横波速度变化则又对相速度起一定影响。这从另一个方向解释了上述反演的结果，也可以看出各层反演得到速度结果的可靠性。

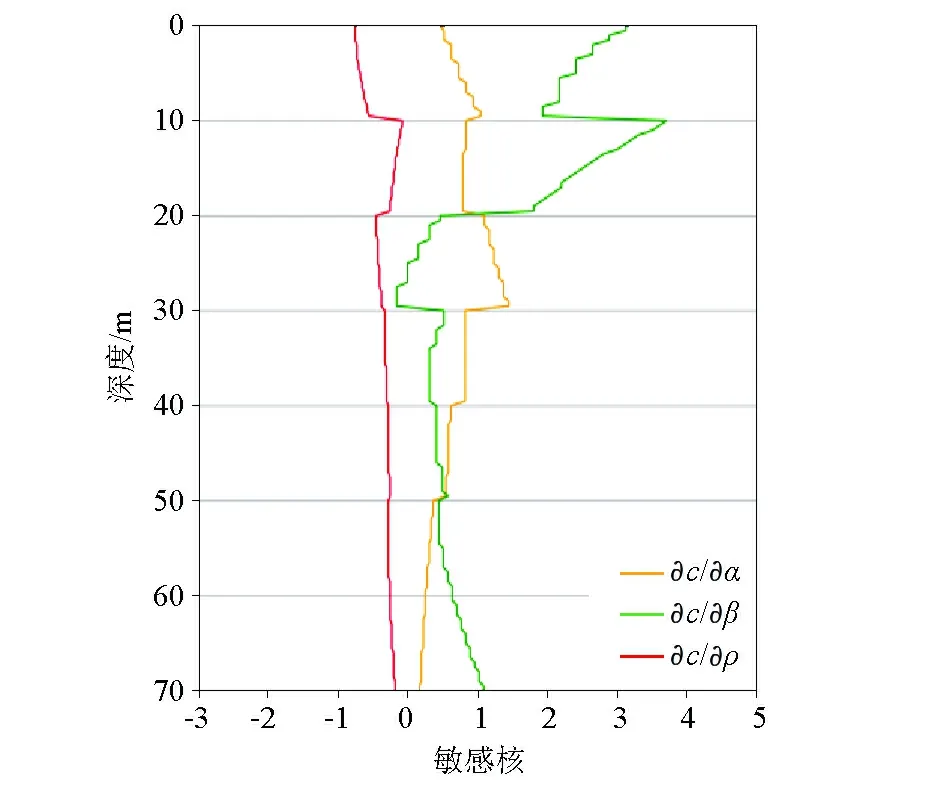
图3 频率为2 Hz瑞利面波相速度敏感核Fig.3 Phase sensitivity kernel of Rayleigh wave on 2 Hz

3 算法稳定性和效率

为了测试算法稳定性和运行效率，这里所有运算过程均使用单CPU核心并且没有其他计算任务在系统平台上运行，系统平台选择Ubuntu以避免其他后台程序干扰。测试使用的处理器为英特尔二代酷睿i5(i5-6200U)主频2.3 GHz，且并没有让GPU参与运算。算法种群规模、迭代次数等参数均使用默认值,且均不加入外部判断是否继续或跳出反演代码。测试结果如图4所示。可以看出差分进化算法拟合度最高，但算法耗时最长；遗传算法和粒子群算法反演耗时大幅度缩短，但拟合度较差；模拟退火法拟合度较好，耗时由于初始模型的选择，这里接近差分进化算法。考虑到默认的种群规模较大，差分进化算法实际使用可以考虑减少数值来提升计算效率。遗传算法和粒子群算法则可以加入合适判定增加反演迭代次数来提高拟合度的稳定性。模拟退火法效率十分依靠初始模型的选择，很适合已有初始模型的反演，但要注意模拟退火其他参数选择也很重要，否则容易出现迭代次数或者温度达到后跳出反演。

a—差分进化算法;b—遗传算法;c—粒子群算法;d—模拟退火算法a—differential evolution algorithm;b—genetic algorithm;c—particle swarm optimization;d—simulated annealing algorithm图4 不同启发式算法的效率和稳定性Fig.4 Efficiency and stability of different heuristic algorithms

scikit-opt软件包还提供多CPU 目标函数计算和GPU加速功能，能成倍提升反演计算速度，并且可以进行断点续行，能有效避免运算过程中部分函数出错导致程序崩溃问题。随着算力的提升，计算机科学的发展，能更好地进行地球物理学反演问题的研究。Zhang等[11]2021年应用大数据先行计算好区域模型的格林函数并储存，然后利于人工智能快速识别并反演震源破裂机制参数，在智能预警地震上取得了突破的进展。如今Python语言已有众多大数据和人工智能算法库支持，需要我们提供封包好的地球物理学正演和反演方法。引入大数据和人工智能，这将是未来地球物理研究重要的方向。

4 实例

前文中提到彭一波[1]在研究中利用obspy软件包提取了海拉尔盆地的两个地震台站间背景噪声互相关格林函数的频散曲线，这里我们对其频散曲线进行一个多层厚度5 km的速度模型反演(图5)。可以看出两个台站之间的地壳以及上地幔平均速度结构：区域的浅层横波速度较小,波速在3 km/s附近,这可能是因为沉积层较厚；在15～25 km处存在低速速层，莫霍面深度在40 km附近。这些与李英康[12]、李皎皎[13]等人研究结论一致。考虑到背景噪声提取的长周期面波频散可靠性较低，上地幔以及深部结构还需结合地震面波进行反演确定[14]。

图5 遗传算法反演海拉尔盆地面瑞利波频散结果Fig.5 Inversion of Rayleigh wave dispersion curve in Hailar Basin by Genetic Algorithm

5 结论及讨论

本文基于Python语言scikit-opt软件包进行瑞利面波频散曲线反演实行方案的研究，给出了频散正演算法在实际反演过程中所遇到频散函数解虚数问题的解决方法，搭建了瑞利面波频散反演地下层状速度结构的平台，为今后研究背景噪声成像、面波勘探提供开源基础。同时对比了scikit-opt软件包中不同启发式算法的效率和稳定性，并利用相速度敏感核探讨了反演结果的可靠性，为使用者在反演算法的选择上提供一些依据。最后对彭一波[1]在海拉尔盆地背景噪声研究提取的频散曲线进行了反演，得到了该区域的地壳和上地幔层状速度模型。

可以看出地球物理正演和反演算法的封包，能为广大研究者提供一个可靠且高效的平台，也为今后接入大数据和人工智能打下基础。本文只进行了基阶瑞利面波频散的一维速度模型反演，现在研究趋势是加入高阶频散进行二维、三维模型的反演，这是将今后继续研究的方向。

致谢：感谢R.Hermann、郭飞等人算法的开源共享。

附录

示例1：基于pysurf96程序包计算瑞利面波基阶频散脚本示例，通过修改mode数值可以计算高阶瑞利面波频散。

示例2：基于scikit-opt程序包中遗传算法反演一维层状速度模型脚本示例。脚本目录需包含三个文件：模型上下边界模型l.model和u.model；反演的目标频散文件m.disp。反演的速度模型结果写入本地文件fit.model。