基于雨课堂和BOPPPS模型的探索式数学分析微课教学设计——以泰勒中值定理为例

金玲玉，房少梅

（华南农业大学 数学系，广东 广州）

一 现状分析

数学分析课程作为各个高等院校数学系各个专业的专业基础课程，数学分析的课程内容是后续实变函数、复变函数、概率论等课程的基础，同时也是学生今后从事数学应用和理论研究的理论基础。数学分析课程一直是教学的重点课程之一，但是数学分析教学内容多，内容包含实数理论、极限论、一元微积分、多元微积分及级数理论等；学习时间跨度长，至少跨越三个学期，有些学校甚至是四个学期的课程。同时数学分析理论知识抽象难懂，学生普遍反映难学，具有一定的学习障碍和畏难情绪。传统课堂教学模式单一，教师以黑板板书或者ppt演示为主，以教师灌输被动式教学为主，同时由于课堂内容多，课堂互动少，学生学习的主动性不高，课堂缺少双向性和互动性。如何利用有限的学时，高效合理地开展数学分析教学，提高教学效果，培养学生的数学素质，这是摆在我们面前的一个重要课题。在迅猛的互联网和大数据发展的时代，我们可以将好的教学平台软件和先进的具有特色的教学方法有效地结合起来进行数学分析教学改革。

二 雨课堂教学特色介绍

清华大学在线教育办公室和学堂在线研发的雨课堂平台的出现，为教育教学带来创新和变革的机遇[1]。雨课堂以插件形式在ppt出现，学生和教师都只需要通过微信登陆，方便快捷[2]。同时雨课堂中多种手段，课堂现场答题、点名、投稿等功能促进师生之间的互动，同时还有板书功能和板书发送功能，可以有效地调整课堂节奏。雨课堂教学结合了板书和ppt的优点，又解决了互动问题。同时教师还可以在雨课堂发布课前预习、课后复习内容，还有设立课堂讨论等板块，这些功能都能很好地提高学生兴趣，改善教学质量[3]。师生通过简便的手机操作即可实现提升师生间的互动，让学生线上线下进行混合式学习，教学更为便捷。主要优势如下：

（一） 课前促动

通过雨课堂平台教师可以在课前提前发送学习资料[4]，推送视频、ppt、试题等资料。通过教师发送的学习资料，学生可以在课前进行有效的自主预习，对于本节课程需要的过往基础知识进行复习，初步学习本节的新的知识点，甚至在雨课堂上标注本节课的知识难点、疑点等。教师通过雨课堂的记录可以了解学生预习的难点和疑点以及学生已有的学习基础。这构成了课前师生的有效的双向互动。

（二） 课中互动

雨课堂设置了多种互动形式。学生通过手机微信扫码报道自动记录学生的考勤。雨课堂的随机点名功能使得教师可以抽查学生回答问题，提高学生在课堂上的关注度[4]。教师提出问题，学生也可以通过投稿功能发布自己的解题方案，教师和同学们可以一起评判解题方案的优缺点。雨课堂ppt可以穿插设置习题，在讲解例题后，可以发布题目让学生即时在手机上解答。雨课堂能自动总结汇集学生的解答正确率，这使得教师充分了解学生的知识的掌握程度。这些手段有效地增强了课堂教学过程中师生之间的互动。

（三） 课后互动

课后教师发布课后习题，学生在雨课堂上解答题目。雨课堂平台使得发布的内容多样化，可以是习题也可以是慕课小视频等。对于习题和试卷，教师可以设置答案，选择题和填空题系统将自动批改，并展示正确答案。学生也可以在讨论区发布自己上课的疑问，教师和学生都可以回答问题。雨课堂提供了教师学生课后互动的一个好的平台。

“雨课堂”的混合式教学模式是大数据下的一个新的创新，特别是大数据处理的优势，学生在雨课堂的学习情况可即时通过雨课堂数据分析后反馈给教师，以便教师根据学生的学习情况调整教学节奏，同时雨课堂提供了多种方式让学生进行参与式学习，这有效地调动了学生的积极性，培养学生的学习能力。这将传统的单向的教师传输模式打造成以学生为中心的双向互动教学模式。

雨课堂平台给予师生全新的体验，课堂效率得到有效提高。学生的学习能动性、师生的互动性得到有效改善，是一种多层次、多角度，互学互用的教学方法。

三 BOPPPS模式介绍

BOPPPS教学模式是加拿大不列颠哥伦比亚理工学院创建并推行的新的教学设计，主张以学生为中心，包含导入（bridge-in）、学习目标（objective）、先测（pretest/assessment）、参与式学习（participatory learning）、后测（post-test）/assessment）、总结（summary）六个教学模块。这种学习模式可以吸引学生注意力、激发好奇心，产生学习动力，并通过先测了解学生原有知识的掌握程度，后测确定学生本次学习的掌握度[5-6]。

引入：在BOPPPS教学中设置教学引入（bridge-in）环节。引入方式包含相关知识引入、实际案例引入[7]等多种引入方式。相关知识引入指通过已经学习过的相关知识引入到新知识。比如学习函数极限的时候，先从已学过的数列极限出发，由于数列是特殊的函数，通过数列极限定义引入到函数极限的定义。具体实例引入指采用具体的案例，数学的实际背景引入，比如说学习定积分时候，先从曲边梯形求面积，变速直线运动等具体实例引入。教学的引入可以提高学生学习的兴趣，加深学生对知识的理解和使用。

目标：教师明确本课程的教学目标。根据学校数学系各专业的人才培养目标设置教学目标。教学目标是教师设置教学过程的指南针。

前测：为了提高学生的参与度和关注度，了解学生的知识基础以便学生调整课堂节奏，可以在课前或者课堂布置测试，了解测试情况。借助现代化的教学软件可以方便学生和教师共同完成这个环节。

参与式学习：教师在教学课前、课中、课后多种方式设计参与式学习。比如教师将知识点分块，对一部分知识点采用教师布置任务，学生分组讨论并讲解，教师总结。或者对于比较难以理解的知识，在教师讲解完知识点后，学生分组讨论知识点的运用，引导学生采用不同的方法解决，并讨论方法的优缺点。

后测：课堂知识讲解完毕后，教师布置测试题目检查学生掌握知识情况，这同时助于学生加强知识的掌握度。

总结：将本次课的内容进行总结。对于重点和难点内容进行强调和梳理。

四 雨课堂和BOPPPS模式相结合的创新型教学模式——以泰勒中值定理为例

雨课堂作为一个教学平台可以很好地实现BOPPPS模式。BOPPPS模式的先测和后测都可以通过雨课堂平台进行发布。并且雨课堂的数据处理可以有效地提供学生先测和后测的结果给学生和教师。雨课堂的弹幕、课堂讨论、分组等功能可以完美地实现参与式学习。

本文基于雨课堂和BOPPPS模型，进行以学生为主体，探索式和创新式为主要导向的新的教学设计。泰勒中值定理是数学分析教学内容中重要的一个定理，但是学生很多时候觉得理论复杂晦涩难懂，是教学过程中的难点之一。下面充分运用雨课堂中多种手段结合BOPPPS模式和探索式教学[8]，以及泰勒中值定理本节的知识特点，给出泰勒中值定理教学设计。

（一） 课前准备（与BOPPPS模式的先测相结合）

在雨课堂发布复习和预习任务，复习柯西中值定理、微分的定义和微分在近似计算中的作用，并预习泰勒中值定理的内容。泰勒中值定理是微分在近似计算的一个推广，同时泰勒定理的证明是需要使用之前学习过的知识点和定理。课前预习和复习可以让学生初步理解泰勒中值定理的由来，复习泰勒定理需要用的知识点。设计柯西中值定理、微分及近似计算的相关习题并发布在雨课堂上（先测）。通过雨课堂数据，教师可以了解学生知识基础，预习的进度，以及预习中提出的疑惑，这些方便教师在授课过程中有针对性地教学。如果测试结果比较差，教师需要在课堂上再次复习柯西中值定理等知识。如果学生测试结果好，预习做得比较好，可以稍微加快讲解的进度。

（二） 课堂教学过程

1.教学目标。

知识技能目标：理解并能证明泰勒中值定理，掌握泰勒中值定理的应用。

思想方法目标：培养学生观察、类比推广、验证的数学思想方法。

情感态度目标：透过现象看本质，通过本质特征得出新的现象。培养学生探索创新精神。

2.问题导入（包含参与式学习）。

复习微分的近似计算，如果函数f(x)可微，则

f(x)=f(x0)+f'(x0)(x-x0)+o(x-x0)

f(x)≈f(x0)+f'(x0)(x-x0)

误差是o(x-x0)。微分近似是以直线代替曲线近似，一次函数近似逼近f(x)的思想，但是误差比较大。我们实际上处理的函数大多数都是初等函数，很多初等函数计算比较复杂。但是初等函数是由基本初等函数的有限次四则运算、复合形成的。基本初等函数中熟悉、容易计算的函数是整数阶幂函数。所以近似计算中常用多项式逼近函数。微分计算是通过一次多项式来逼近函数。泰勒中值定理实质上是一个用n次多项式逼近的n阶可导函数的近似表达式。

为了引导学生思考如何提高近似的精度，提问：

（1）可否通过二次函数逼近，n次函数逼近？这样能不能减少误差，提高精度，精度是多少？

（2）如果能够提高精度，对于函数可导性要求有没有提高？

这里可以通过雨课堂投稿的方式，开启弹幕功能和投稿功能，让学生积极地参与课堂活动，促进师生互动，启发学生进行思考，引导出结论。在函数的可导性增强的条件下，用n≥2次多项式逼近函数f(x)，误差减小，误差估计为o((x-x0)n)。透过现象看本质，培养数学素养。

（1）为什么采用n次多项式近似逼近。用熟悉代替不熟悉的，复杂的事情简单化。多项式最熟悉、计算最简单。

（2）误差减少，精度得到提高。函数的条件要求应该增强。在研究过程中，定理的条件增强的前提下，定理的结果也得到提升。

3.泰勒公式的推导。

泰勒公式本质是运用n次多项式逼近函数f(x)。将泰勒公式的推导及证明分三部分来进行。

第一部分，观察逼近的一次多项式和函数f(x)的本质特征，可以设置雨课堂课件中的选择题。此处设置雨课堂选择题既可以引导学生找出问题的本质特点，也可以通过此种方式提高学生的课堂参与度。观察一次多项式p1(x)=f(x0)+f'(x0)(x-x0)的特点，具有（ ）

A.p1(x0)=f(x0) B.p'1(x0)=f'(x0) C.p1''(x0)=f''(x0)

通过此选择题使学生明白近似多项式p1(x)和函数f(x)在x0处相等，且对应的一阶导数也相等。对比预测近似多项式pn(x)和函数f(x)在x0处相等，且对应的n阶导数也相等。此处培养学生观察和类比的数学方法。

第二部分，根据预测的特点，采用待定系数法求出pn(x)。设：

计算pn(x)的各阶导数，带入x=x0上面表格中等式，引导同学们一起计算系数an并得出：

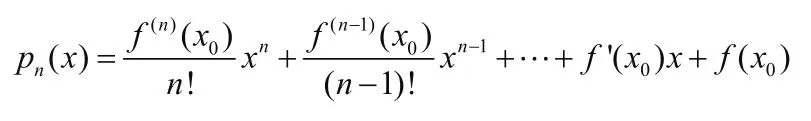
这部分内容训练了同学们的计算能力。第三部分是泰勒中值定理的证明。从近似计算中误差估计的角度出发看，验证探索找到的泰勒多项式pn(x)的确是近似逼近f(x)，且误差为o((x-x0)n)。即验证余项：

证明讲解中注意以下问题：

（1）分别采用柯西中值定理和洛必达法则这两种不同方法进行证明，引导学生注意方法的差异。

（2）如果将函数f(x)的n阶可导条件加强为n+1阶可导，可以得到余项（误差）的精确表达式。近似估计式变成一个恒等式[6]。

ξ介于x到x0之间。

（3）泰勒公式是拉格朗日中值定理的推广。当x0=0时，泰勒公式又称为麦克劳林公式，麦克劳林公式使用最为广泛。

4.泰勒公式的应用（后测）

（1）泰勒公式在计算中的应用：

①近似计算中的运用：

②极限运算中的运用：

（2）泰勒公式在证明中的应用：

此类题目核心在于右边是多项式，所以需要尝试将左边用泰勒公式展开为多项式加余项。

5.总结

（1）教学内容的总结

总结本节课的主要内容，泰勒中值定理的各种形式，泰勒中值定理的证明，泰勒中值定理在近似计算、极限计算、证明中的应用。

（2）数学思想的总结

从微分近似以直线（一次多项式）代替曲线（一般函数曲线）出发到以曲线（熟悉的n次多项式）代替光滑曲线（任意n阶可导的曲线）的数学思想，学会先观察，数形结合，找到事情的本质特点，类比推广、大胆尝试，谨慎验证的数学方法。这些方法可以用到其他问题的研究上。学数学知识的同时要善于学习数学方法，培养数学素质。

五 应用反思

泰勒中值定理的教学设计，从微分的近似应用出发，引导学生观察微分近似的本质特征，图像（以直代曲）和代数（一次多项式）近似替代可导函数两个方面的特点，抽象出事情的本质特征。从解决实际的应用的需求，提高误差的精度出发，引导学生尝试解决问题，找出近似逼近函数的n次多项式，并验证结果。采用了问题驱动、对比教学、数形结合等教学方法，促进学生积极地参与学习，主动学习。在学生从发现问题，抽出问题的本质特征，尝试提出解决问题的方法并证明方法的正确性的过程。这个教学设计式融合了BOPPPS模式和探索式学习的特点，教学过程通过雨课堂作为媒介，有效地促进了师生的互动交流，BOPPPS模式中先测和后测环节的实施等。

在数学分析的教学过程中，实行基于雨课堂和BOPPPS的探索式学习，是大数据环境和教学改革创新相结合的一个模式。这个模式充分利用雨课堂平台，实现了BOPPPS的以学生为中心，参与式学习、探索式学习为核心的新的教学模式。该模式可以提高数学分析教学效率、有效地促进师生互动，学生的主观能动性得到大大的提高。