Pasternak地基中盾构施工对斜交管线的影响分析

■熊晨超，陈 飞，王春国

（义乌工商职业技术学院，浙江 义乌 322000）

地铁隧道施工会引起土体扰动现象，土体扰动会引起土体周围区域的地下管线变形。而城市地下存在大量市政工程和工业用的管线，纵横交错的地下管线给隧道施工带来极大的挑战。实际施工过程中地下管线网布局极其复杂，不会是纯粹的管隧平行或管隧垂直状况，为深入研究复杂的管隧位置关系对地下管线的影响规律，本文专门研究斜交于盾构隧道的地下管线的性状变形规律，为进一步研究实际盾构开挖下复杂状况的地下管线网提供有效依据。

一、管隧斜交时管线受力机理

当管线和隧道斜交时，计算模型见图1。

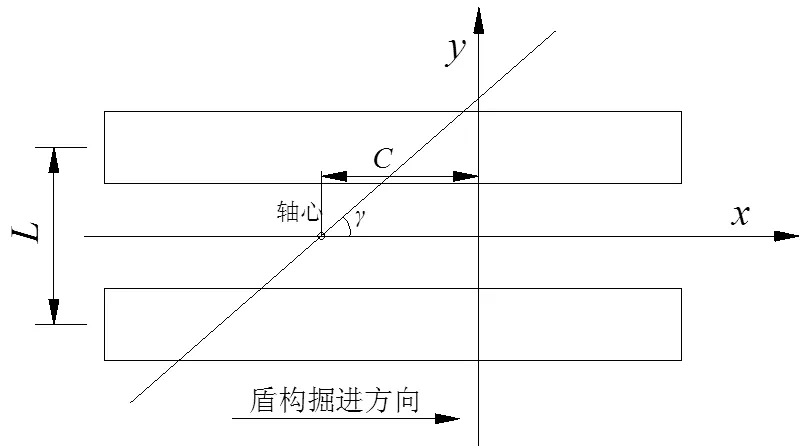
图1 管隧平行计算模型

假设管线无限长且斜交于x轴，夹角为γ，x轴为双线盾构中轴线，双线盾构开挖面在x=0位置处，管线与x轴的交点到y轴的距离为C。隧道轴线方向与x轴方向平行，掘进方向为负；管线轴线方向也与x轴方向平行，以向右为正；z轴与地面垂直，以向下为正。

二、管隧斜交时的管线受力与变形计算

（一）管线竖向位移计算

设管线计算点的横坐标为x=x0，则其纵坐标为y=(x0-C)tanγ。结合文献[1]的内容，可得到单线盾构施工中管隧斜交时，连续管线计算点所受位移大小：

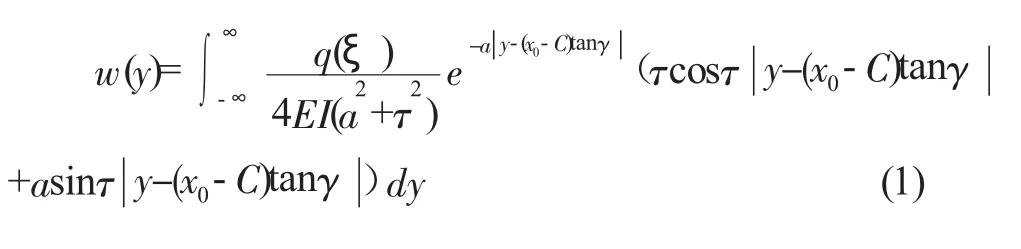
在单线盾构穿越引起管线沉降的基础上，可得出双线隧道穿越后造成管线竖向位移的计算公式。两者叠加后，即可计算出双线平行盾构隧道施工引起的总的管线竖向位移隧道w为：

（二）管线弯矩及应力应变计算

对于无线长梁，在Pasternak地基上一点作用集中荷载P，管隧斜交时，管线在隧道开挖影响区域范围内的任意一点的弯矩计算式为：

三、算例分析

（一）标准工况算例

标准工况说明：工程为双线盾构隧道施工，在双线隧道中轴线正上方有一地下管线斜向穿过，管线走向与盾构轴线夹角γ=45°。管线材质为钢筋混凝土管，规定隧道在黏土中开挖。具体计算参数如下。隧道参数：h=15m，R=3m，L=13.2m；管线参数：计算点C=0m，d=0.8m，z0=6m，EI=480000 kN·m2；土体参数：E0=3.0876 MPa，μ=0.3。假设ηf=0.5%，根据魏纲建议 ηl/ηf=0.0283h+0.6933得到ηl=0.56%，并假定右侧隧道先开挖，af=0.3R，al=0，b=0，y=0。其他参数与单线隧道开挖情况一致。

图2和图3所示分别为管隧斜交工况下离开挖面不同距离时双线隧道和先行隧道施工后管线竖向位移的曲线图。如图2和图3所示：(1)先行隧道施工引起管线的最大竖向位移值随着C值的变小而变大，且最大位移值所处管线位置随C值的减小而偏向开挖面后方，这是由于地下管线随着C值的减小而靠近开挖面后方，而开挖面后方10 m内土体工后沉降尚未稳定；（2）不同C值工况下双线隧道施工引起地下管线的竖向位移曲线变化规律与单线隧道一致，最大竖向位移值随着C值的变小而变大，且双线隧道的影响范围更大。

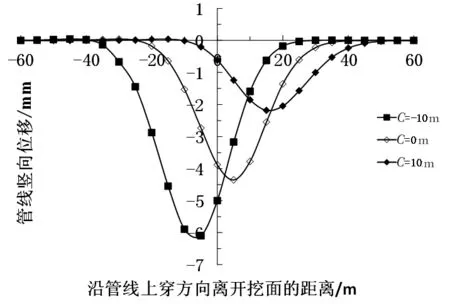
图2 先行隧道施工引起的地下管线竖向位移

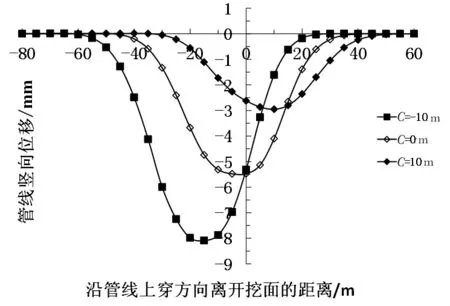
图3 双线隧道施工引起的地下管线竖向位移

图4 所示为管隧斜交工况下离开挖面不同距离时先行隧道施工引起的地下管线弯矩图。如图4所示：(1)C=0 m时管线弯矩曲线有一处正弯矩峰值、两处负弯矩峰值，其中在离开挖面后方管线长度为-10 m处管线受到的最大负弯矩为-20.59 kN·m，在离开挖面前方管线长度为25 m处管线受到的负弯矩峰值为-3.99kN·m；在离开挖面前方管线长度为10 m处管线受到的最大正弯矩为29.04 kN·m；(2)不同C值工况下单线隧道施工引起地下管线弯矩曲线变化规律相同，管线最大正负弯矩值均随C值的减小而增大，且其所处位置随C值的减小而偏向管线后方。本研究同时计算得到离开挖面不同距离时双线盾构引起的管线弯矩曲线 (见图5)。如图5所示：(1)不同C值时双线隧道施工引起地下管线弯矩曲线变化规律与单线隧道并不相同，C为-10m和0 m时管线弯矩曲线有两处正弯矩峰值、两处负弯矩峰值，且C=-10 m时管线正负弯矩峰值均大于C=0 m时管线正负弯矩峰值。(2)C=10 m时管线弯矩曲线有一处正弯矩峰值、两处负弯矩峰值，这是由于在管线-10 m到10 m位置处，先行隧道施工引起的负弯矩值均大于后行隧道施工引起的管线正弯矩值，曲线仅在管线0 m位置出现拐点。

通过比较图4和图5，发现单线盾构和双线盾构引起的管线弯矩峰值均随C值的减小而增大，其所处位置也在不断地靠近管线后方；双线盾构引起的管线最大正负弯矩值均要小于单线盾构引起的管线最大正负弯矩值，这与管线竖向位移变化规律不同。

图4 先行隧道施工引起的地下管线弯矩图

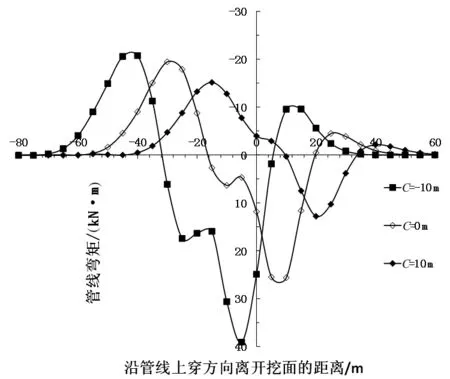
图5 双线隧道施工引起的地下管线弯矩图

（二）管隧斜交角度的影响

当地下管线与隧道斜交时，管线与隧道轴线的斜交角度是反映管线与隧道相对空间位置的一个主要参数。取管隧斜交角度分别为30°、45°、60°，研究地下管线受盾构隧道施工影响的性状。图6所示为先行盾构施工引起的地下管线位移曲线与斜交角度的关系，如图6所示：(1)γ为30°、45°和60°时管线最大竖向位移值分别为4.88 mm、4.36 mm和4.08 mm，管线最大竖向位移值随着斜交角度的增大而减小；(2)管线竖向位移曲线影响范围随着γ的增大而减小；(3)管线最大竖向位移值均位于离管线零距离点5 m位置处，即单线隧道引起的管线最大竖向位移所处位置不随γ值变化而变化。图7所示为双线盾构施工引起的地下管线位移曲线与斜交角度的关系。由图7可知：(1)斜交角度的变化对地下管线竖向位移曲线形状影响较大，γ为45°和60°时地下管线沉降曲线符合正态分布规律 (即V形)，γ为30°时地下管线沉降曲线呈W形分布；(2)双线盾构施工引起的地下管线位移曲线影响范围随着斜交角度的增大而逐渐减小；(3)γ为30°、45°和60°时管线位移最大值分别为5.51 mm，5.48 mm和5.47 mm，即双线盾构施工引起的地下管线最大位移随着斜交角度的增大而逐渐减小。

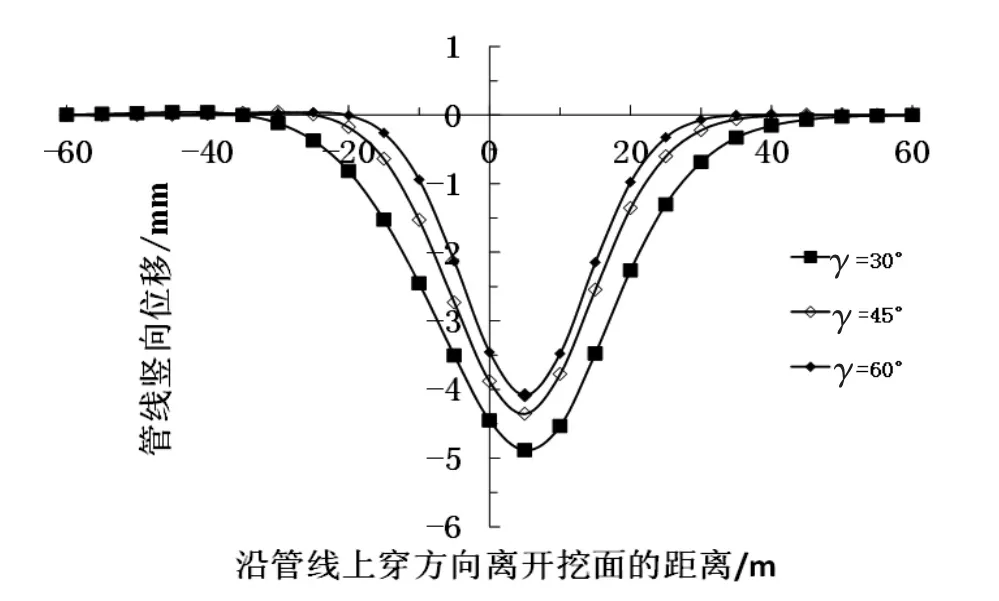
图6 不同斜交角度下先行盾构引起的管线位移曲线图

图7 不同斜交角度下双线盾构引起的管线位移曲线图

图8 所示为先行盾构施工引起的地下管线弯矩曲线与斜交角度的关系。如图8所示：(1)γ=30°、45°和60°时管线最大正弯矩分别为33.37 kN·m、29.04 kN·m和28.63 kN·m，管线最大负弯矩分别为-22.92 kN·m、-20.59 kN·m和-18.11 kN·m，管线最大正负弯矩值均随着斜交角度的增大而减小；(2)管线弯矩曲线影响范围随着γ的增大而减小。图9所示为双线盾构施工引起的地下管线弯矩曲线与斜交角度的关系。如图9所示：(1)γ为30°、45°和60°时管线最大正弯矩分别为31.67 kN·m、25.66 kN·m和 24.04 kN·m，管线最大负弯矩分别为 -21.66 kN·m、-19.45 kN·m和 -16.89 kN·m，管线最大正负弯矩值均随着斜交角度的增大而减小；(2)γ为30°、45°和60°时管线弯矩曲线均有两处正弯矩峰值和两处负弯矩峰值，且管线弯矩曲线影响范围随着γ的增大而减小。通过比较图8和图9，可以发现单线和双线盾构引起的管线最大正弯矩值所处位置均随着斜交角度的增大而偏向管线零点位置，这是由于随着γ值的增大，管线与隧道轴线的夹角越接近垂直状态，管线最大弯矩因此越靠近隧道轴线位置。

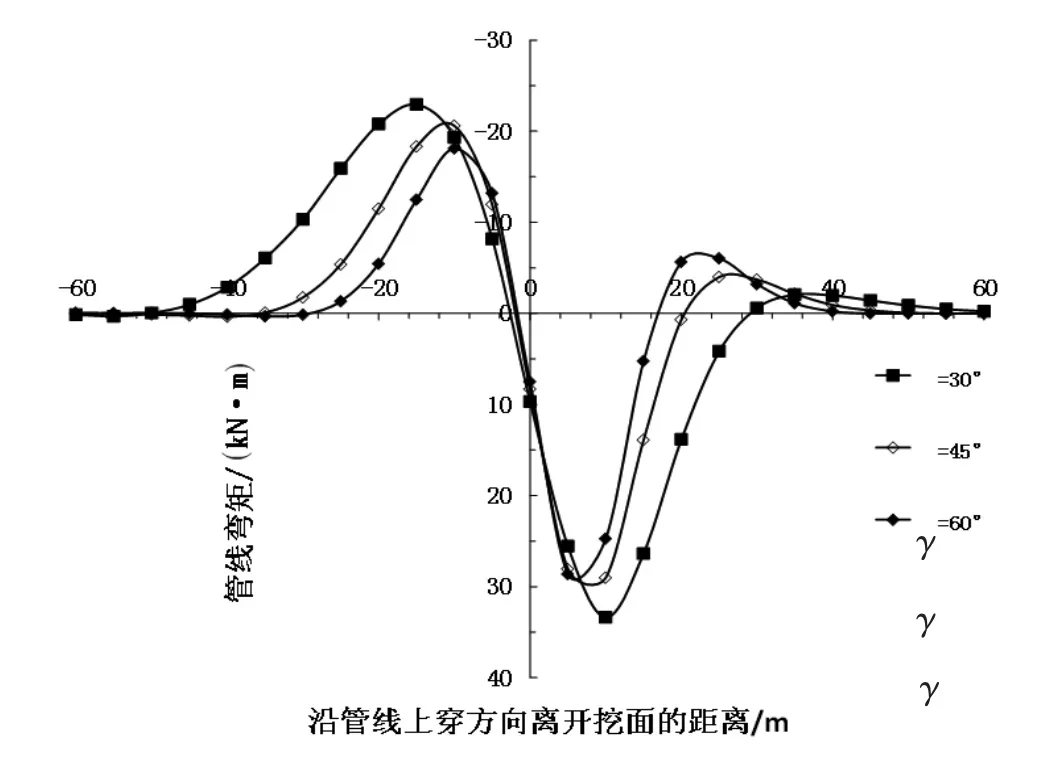
图8 不同斜交角度下先行盾构引起的管线弯矩曲线图

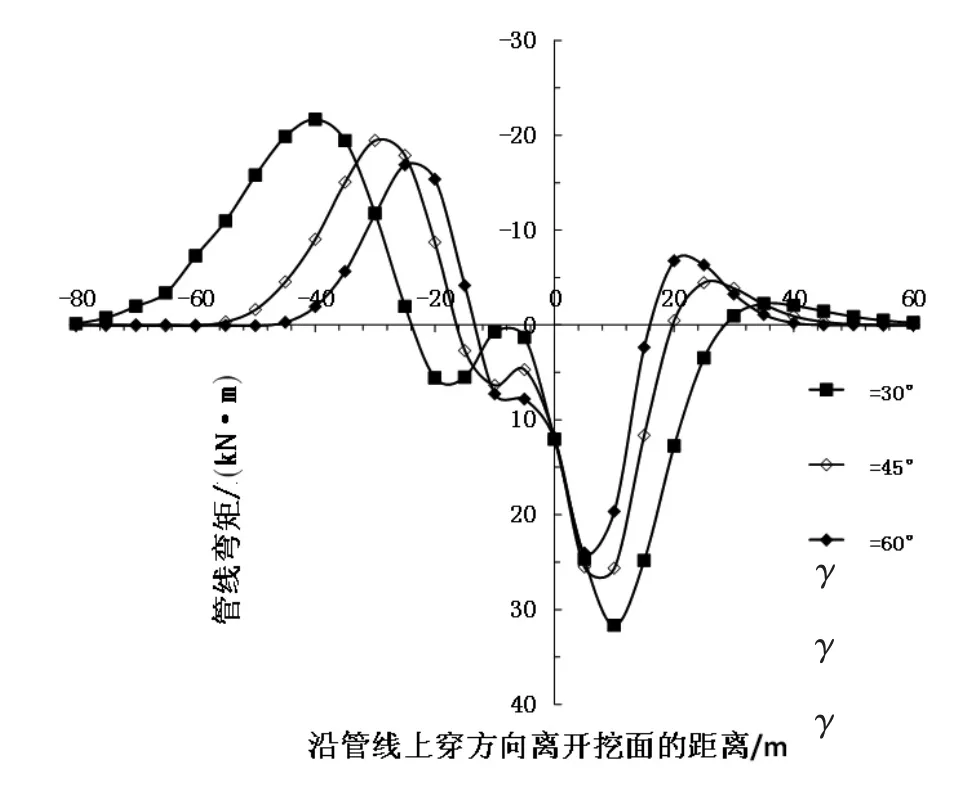
图9 不同斜交角度下双线盾构引起的管线弯矩曲线图

四、结论

1.本研究采用盾构法隧道统一土体移动模型三维解，结合文献[1]建立的双线盾构中土体损失引起的土体沉降计算方法，基于Pasternak地基模型，推导出管隧位置斜交时，盾构隧道施工引起的管线弯矩、应力、应变和变形的计算公式，通过算例分析，表明本研究方法的合理性，为隧道开挖引起地下管线的受力和变形的预测提供帮助。

2.算例分析表明：管隧斜交工况下离开挖面不同距离时先行隧道和双线隧道施工后管线竖向位移曲线变化规律相同，最大竖向位移值均随着C值的变小而变大，而其所处管线位置均随C值的减小而偏向开挖面后方，且双线隧道的影响范围更大；不同C值时单线隧道施工引起的地下管线弯矩均有两个负弯矩峰值、一个正弯矩峰值，且管线零位置后方引起的管线负弯矩峰值均要大于管线零位置前方引起的管线负弯矩峰值；不同C值时双线隧道施工引起的地下管线弯矩曲线与单线隧道时并不相同、有两处正弯矩峰值，两处负弯矩峰值单线隧道，且其影响范围也更大，但两者的弯矩最大值均随着C值的变小而变大。

3.单线隧道施工引起的管线最大竖向位移值、最大正负弯矩和影响范围均随斜交角度γ的增大而减小，且最大竖向位移所处位置不随γ值变化而变化；双线盾构引起的管线最大正负弯矩值、弯矩影响范围均随着斜交角度的增大而减小；斜交角度的改变对双线盾构引起的地下管线竖向位移曲线影响较复杂，呈现“W”形和“V”形两种情况，随着γ的增大，曲线形状从“W”形向“V”形变化。