基于粗糙集理论和优劣解距离法的邮轮舱室舒适性评价
姚竞争, 王同山, 陈哲,3*, 于珍珍
(1.哈尔滨工程大学船舶工程学院, 哈尔滨 150001; 2. 山东交通学院船舶与港口工程学院, 济南 250357; 3. 山东科技大学先进制造技术中心, 青岛 266590; 4. 招商局金陵船舶(威海)有限公司, 威海 264205)
近年来,随着国民经济的发展和生活水平的提升,邮轮旅游业在近几年迅速发展[1]。邮轮作为以娱乐性为核心的旅游载体,舒适性要求也不断提高。邮轮舱室舒适性指标数目较多、数据分散较大,且相当部分数据需要通过乘客主观感受取得,容易受到乘客主观性影响而缺乏精确性。在实践中常常采用粗糙数来应对数据的不确定性,例如,周勃等[2]在对室内环境进行评价时,引用粗糙集理论,约简化了不必要的属性,为室内环境设计提供了参考依据。
粗糙集理论(Rough set)具有处理不精确、不一致、不完整信息的优势。由于研究中的一些指标依赖于评价者的主观评判,并且带有一定的不确定特点,采用粗糙集进行评价能够减少主观评价带来的偏差[3]。但仅依赖于粗糙集,难以形成完善的评价体系。优劣解距离(technique for order preference by similarity to an ideal solution,TOPSIS)法对数据散布、样本量多少、指标多少没有具体的要求,且数学计算量较小,具备比较直观的几何意义。TOPSIS法作为一种常见的传统的多准则决策(multi-criteria decision making,MCDM)评价方法,在一些领域被广泛应用,如机械、医疗、工业和经济等,并在多领域被证明是可靠且有效的评价方法[4],但TOPSIS法在处理不确定问题中,过分依赖评价者主观评价结果,容易造成错误的结果。
目前,国内外对邮轮舱室舒适性的研究多以单一指标或具有关联性的指标作为研究对象,且研究方法的选择易受主观因素的干扰,对实验结果有一定的影响。例如,薛斌[5]对舱室舒适性研究中,只研究了舱室内振动、噪音对舒适性的影响;Massimiliano等[6]将个性化的主题客房作为邮轮舱室舒适性影响指标,影响指标过于单一,忽视了其他指标对舒适性的影响。柳化松[7]提出了一种基于层次分析(analytic hierarchy process,AHP)和模糊综合评价(fuzzy comprehensive evaluation,FCE)的模糊层次分析的邮轮舱室舒适性评价方法,但该评价方法对指标权重依赖于评价者的主观判断,影响评价结果。
现运用粗糙集和TOPSIS法相结合,提出一种较为客观的邮轮舱室舒适性评价方法,与其他评价方法相比,该方法不易受主观因素的影响,不受样本数量的限制,不仅适用于少样本问题,对多样本问题同样适用,且最终结果可得到较为直观的表达。利用粗糙集理论确定邮轮舱室舒适性指标的权重,再通过TOPSIS法计算评价方案与最优值的接近度,不仅克服TOPSIS法权重计算的主观性问题,还能对评价结果进行直观排序。
1 概述
邮轮舱室舒适度的评价涉及噪声、振动、光照、舱室空间等多方面因素,属于多准则决策(MCDM)问题。多准则决策问题是一种复杂的方案选择性问题,针对此类问题,常见的解决方案有5种,如表1所示[8]。
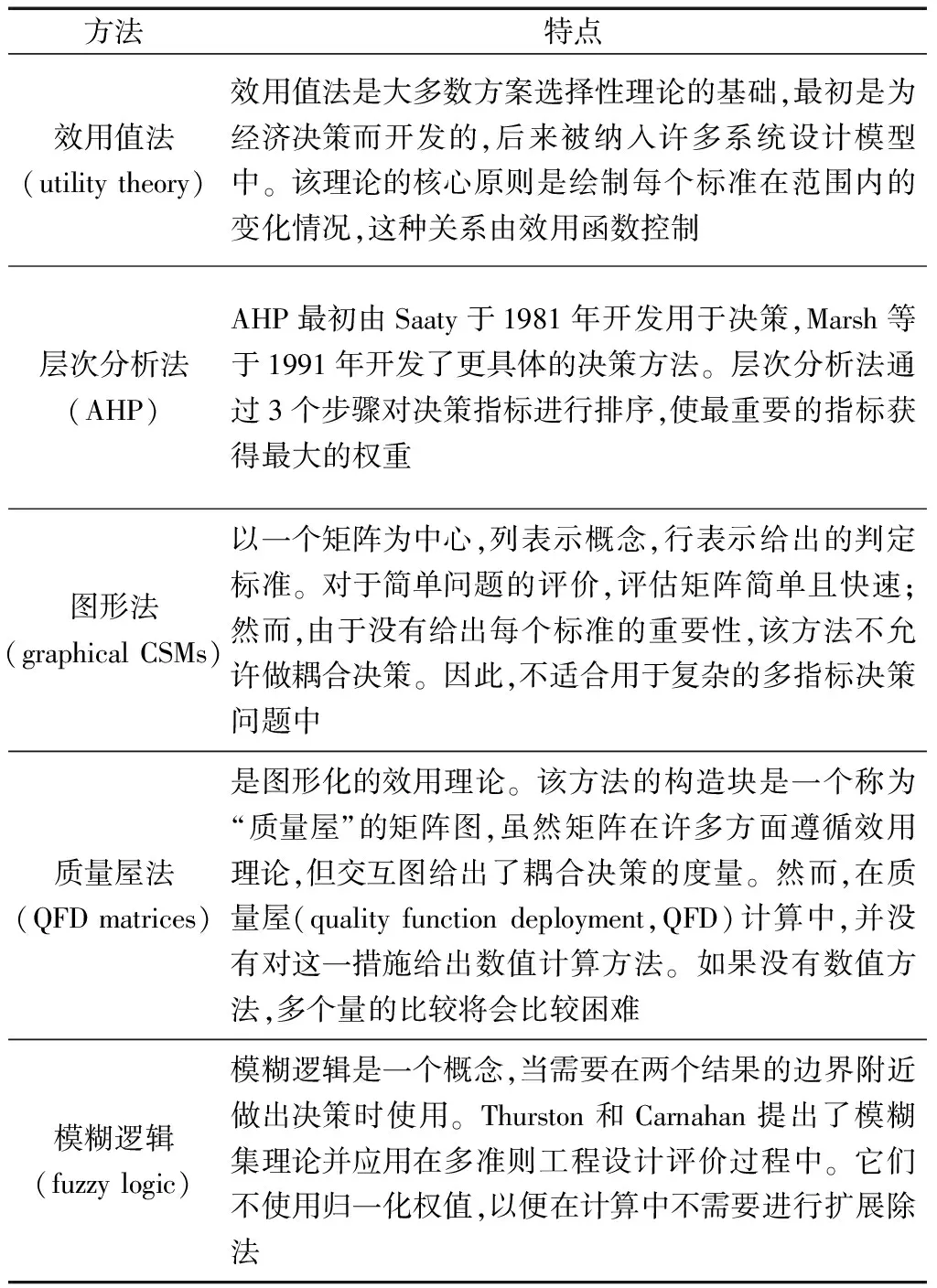
表1 5种常见的MCDM问题解决方案[8]Table 1 Five common solutions to MCDM problems[8]
在表1所示的5种评价方法中,模糊理论作为一种常见的评价方法,由于其在处理主观的、不确定问题中具有优势,自20世纪60年代Zadeh[9]将模糊集引入应用于MCDM问题的解决后,就备受推崇,多种形式的改良型模糊集在实际不确定决策项目中应用[10-11]。但模糊集本身存在主观性,依赖于对外界条件的假设,容易受主观因素影响[12]。相比较而言,粗糙集只依赖其内部信息,无需引入外界条件,在数据处理方面更具有优势。
1.1 粗糙集
粗糙集最早由波兰数学家Pawlak提出[13],该理论能够对不精确、不一致、不完整信息与知识进行分析和处理,广泛应用于各种不确定环境中。在船舶优化、故障诊断领域,也有一定的应用研究[14-15]。董素贞[16]在对船型优化研究中,将粗糙集应用于船型空间缩减的优化过程中,既保证了整体优化,又提高了优化效率。Lu等[17]在运用粗糙集理论判定船舶在光学遥感图谱中的特征,并结合径向基函数(radial basis function,RBF)神经网络进行有效监视。在多指标决策中,粗糙集应用也非常广泛[18-19]。
粗糙集理论是一种数学工具,它利用给定数据中固有的信息,而不需要任何辅助信息或主观判断(如模糊集理论中的隶属函数)来分析数据。它使用近似空间、集合的上下近似等近似运算符来处理模糊性和不确定性。一般来说,粗糙集理论使用一组包含多值属性的对象来分析任何数据。这种对象结构称为信息表。
利用粗糙集理论的上下近似,定义了粗糙数和粗糙边界区间。在数学上,粗糙数的定义如下。


(1)
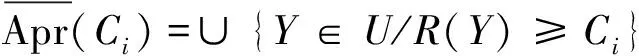
(2)
在一组有序数据中,信息表中的所有对象,数值等于或小于C的对象构成C的下近似,同一信息表中,数值等于或大于C的对象构成C的上近似,信息表中所有指标值不同于C的对象构成C类的边界区域,即
Bnd(Ci)=∪{Y∈U/R(Y)≠Ci}
={Y∈U/R(Y)>Ci}∪
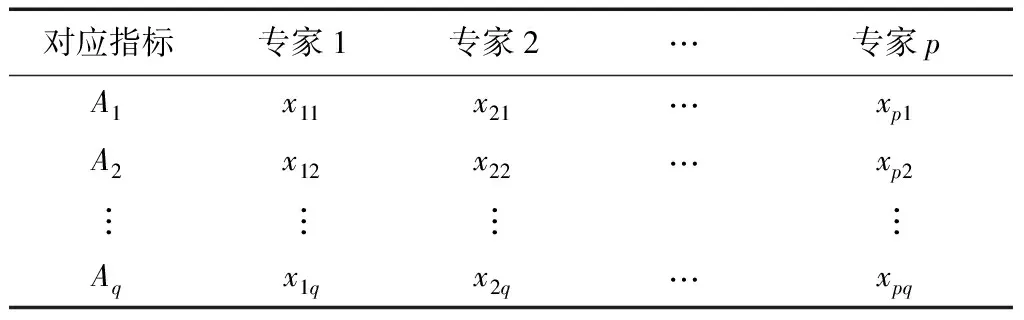
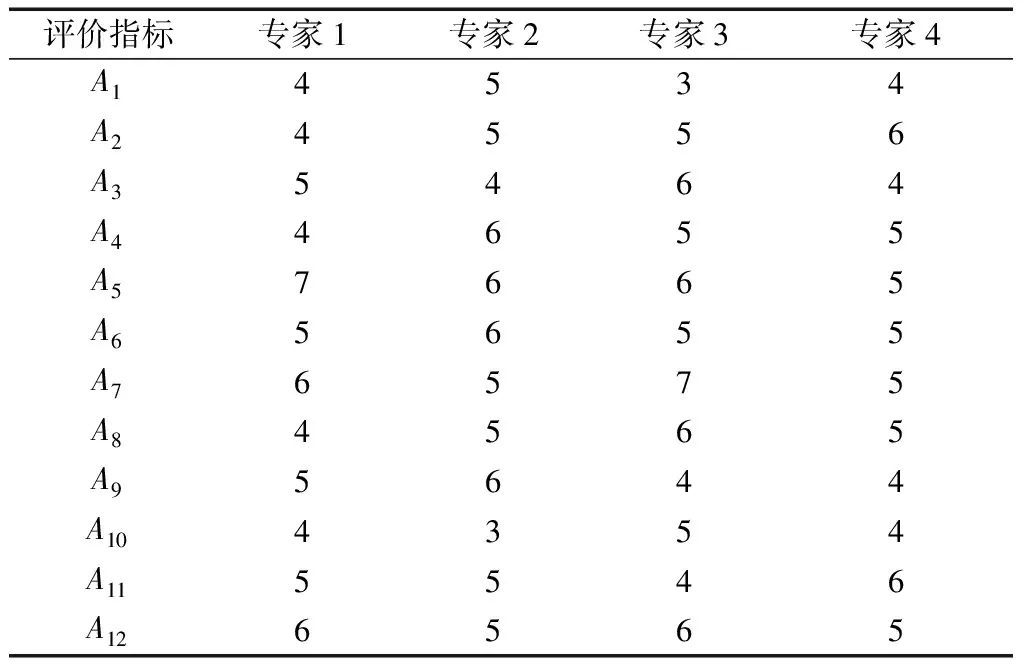
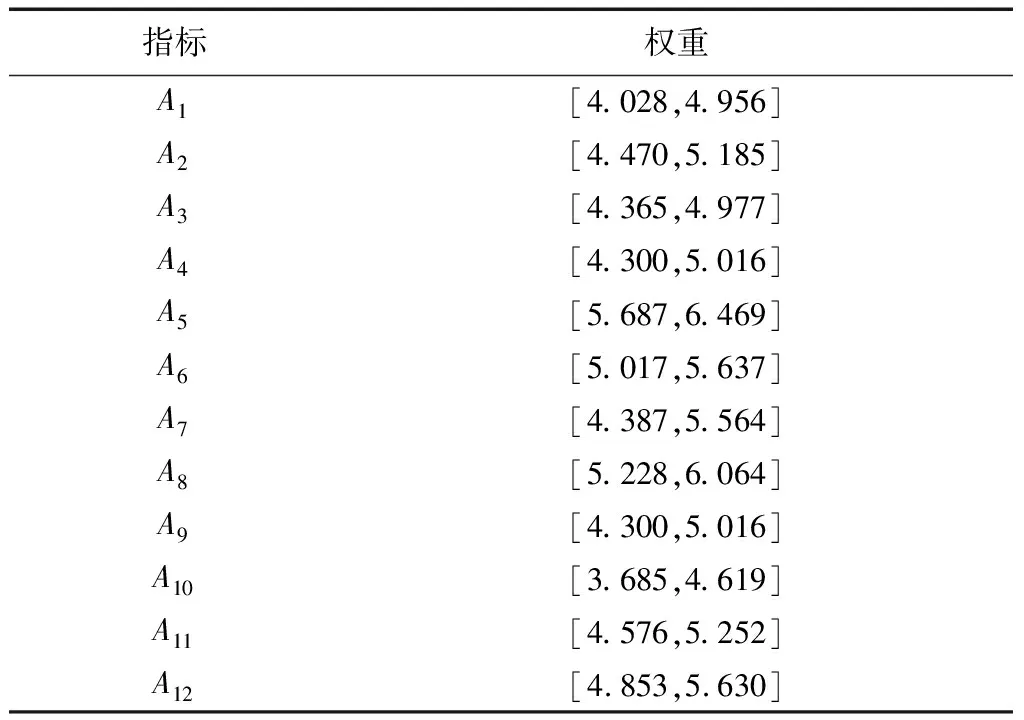
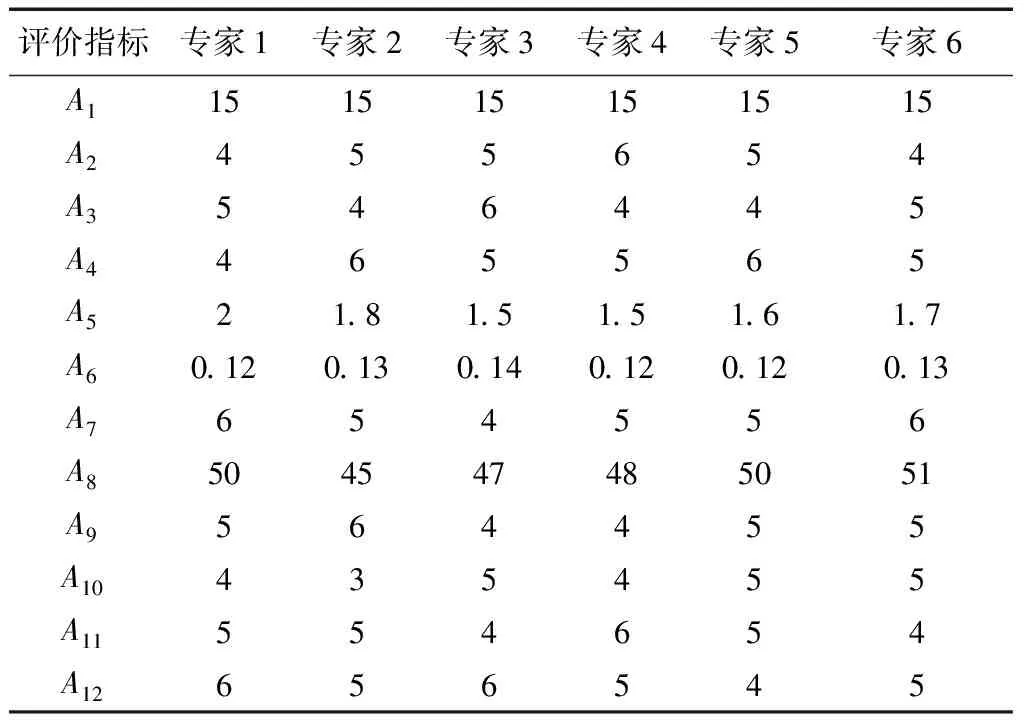
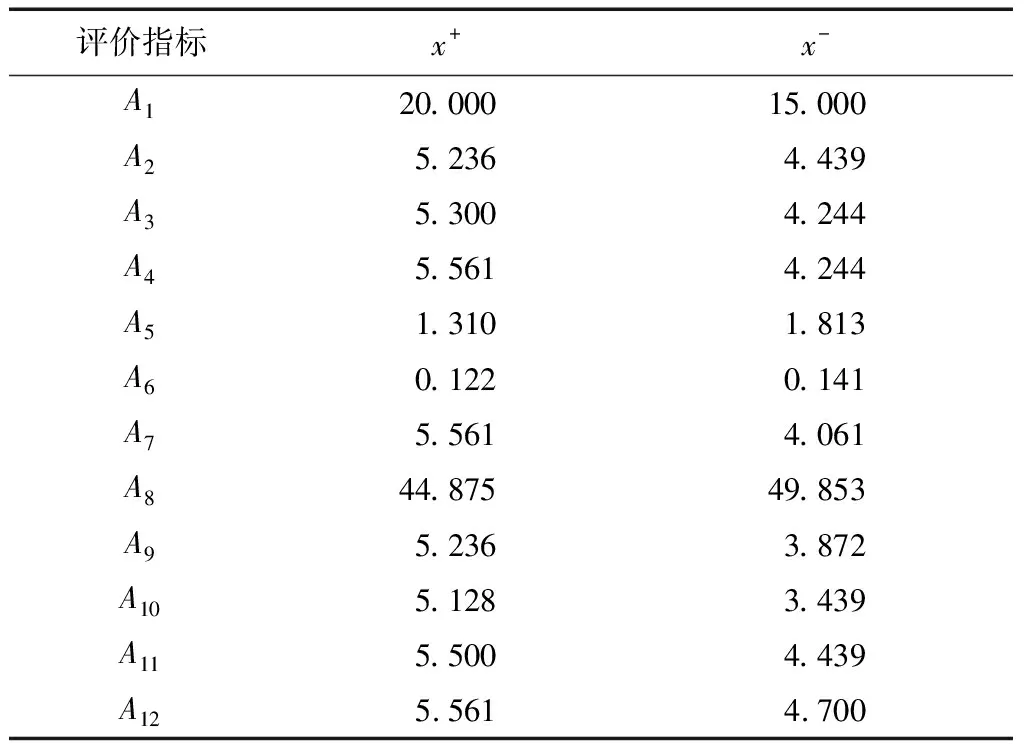
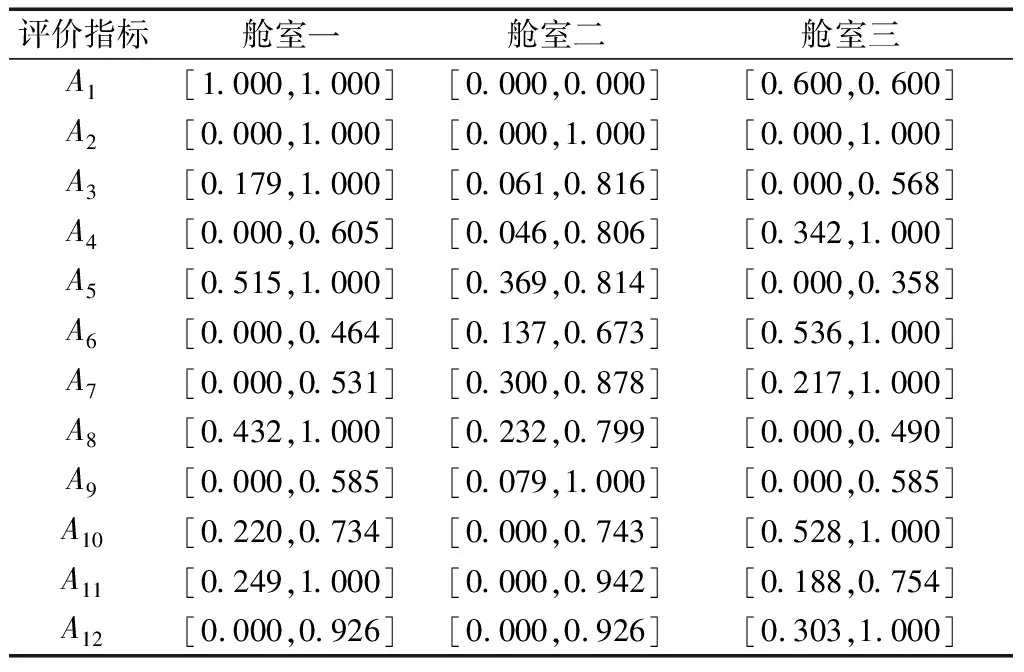
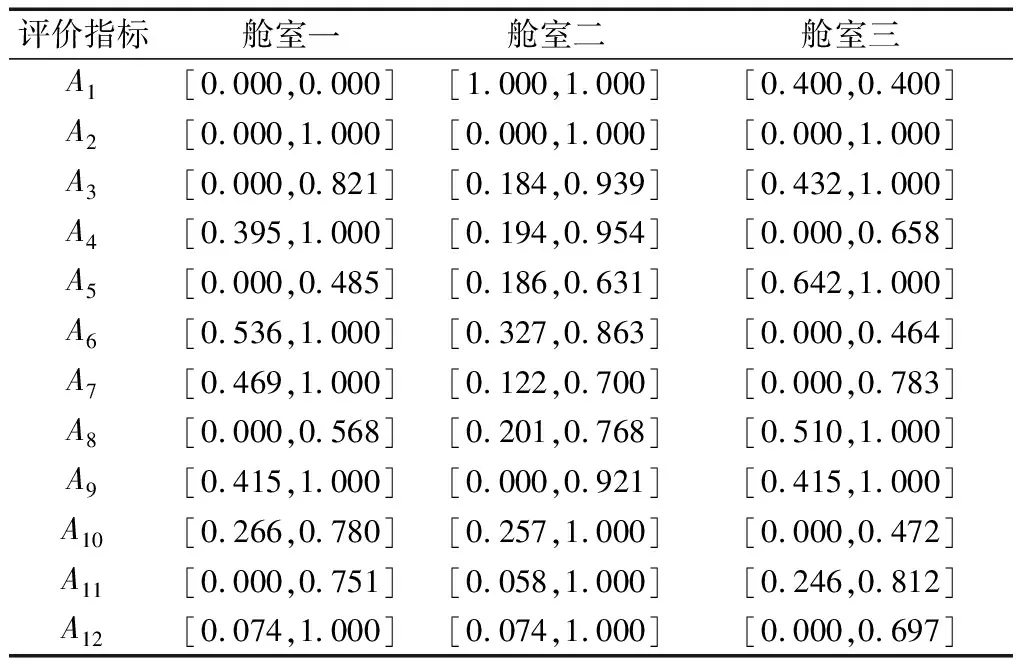
{Y∈U/R(Y) (3) (4) (5) 式中:ML、MU分别为Ci下近似和上近似包含的对象数。 所以粗糙数和粗糙边界区域区间可以用上限跟下限表示,粗糙数的公式为 (6) 粗糙边界区域的公式为 (7) 粗糙集作为一种处理主观不精确数据的方法,能够较好地应对主观数据处理问题,但难以独立解决MCDM问题。近年来,学者们采用三角形、梯形以及钟形分布数,网络分析法以及遗传理论等都与粗糙集理论结合被应用于MCDM决策评价当中[20-22]。但实际决策过程中却常因数据难以取得而无法进行[23]。在实际操作中需要结合传统的MCDM方法框架才能形成有效的评价模型。 运用传统多指标评价方法,结合粗糙集理论,是解决实际问题的较为有效的手段。多准则妥协解排序方法(vlseCriteria optimization and compromising resolution,VIKOR)和TOPSIS是目前解决MCDM问题最为常用的两种方法。粗糙集与VIKOR法或TOPSIS法结合的综合评价方法,被有效应用于生产生活中多个领域,取得了显著的效果。Tiwari等[18]提出了基于粗糙集和改良的VIKOR的评价方法,并运用该方法进行了试验台的设计评价,并通过对比验证了其科学性。周福礼等[24]在对汽车质量改善的研究中,综合考虑消费者抱怨等不确定因素,运用梯形模糊数结合熵权-VIKOR方法,建立质量改善模型,并运用实例证明该方法之有效性。在综合对比VIKOR与TOPSIS法后,TOPSIS法具有更好的区分度,也是解决MCDM问题的更优的选择[4]。 TOPSIS法作为一种多目标决策分析的有效方法,通过比较现有方案与正理想解的接近程度,评价现有方案的相对优劣。由于TOPSIS法对数据散布,样本量多少和指标多少没有具体的要求,且数学计算量较小,具备比较直观的几何意义。张远等[25]采用组合赋权-TOPSIS法对港口分货类竞争力进行评价,拓展了TOPSIS法的应用范围。Zhu等[26]综合运用粗糙集、层次分析法和TOPSIS法,对9款不同的汽车热交换机进行了对比,基于11个评价指标,取得了良好的效果。展现出该方法对多指标评价的有效性。 TOPSIS法是通过检验评估指标与最优解、最劣解的距离来进行排序的。TOPSIS法的步骤如下。 步骤1计算权重标准化值,构建关于权重标准化值的权重标准化矩阵。 (8) 式(8)中:Cmn为第m个方案的第n个评价指标的权重标准化值,Cmn=X′mnWn。 步骤2按照TOPSIS法,确定正理想解C+和负理想解C-。 (9) (10) 步骤3计算距离尺度。方案到正理想解C+的距离为S+;到负理想解C-的距离为S-。 (11) (12) S+为各评价方案与最优方案的接近程度,S+值越小,评价方案距离理想方案越近,方案越好。计算与正理想解C+的相对贴近程度,其相对贴近度CI为 CI=S-/(S++S-) (13) 步骤4进行排序。根据CI的值按从小到大或从大到小的顺序对各评价方案进行排列。CI表示该备选方案与正理想解的贴合程度,排序结果贴近度CI值越大,表示该方案越优。 研究将采用粗糙集结合TOPSIS法建立邮轮舱室的舒适度评价模型。 邮轮舱室的舒适度取决于诸多因素的综合影响。程远等[27]以设计更为人性化的舱室家具为切入点,运用色彩心理学、形态美学和人机工程学等理论,总结了色彩、功能、形态、材质、人机匹配等影响邮轮舱室舒适度的影响因子。舒适度作为主观的体验,依赖于人的器官,同一感官对应不同指标方便类比,形成体系。故从感官舒适性的角度出发,从视觉、触觉、听觉、嗅觉、味觉角度出发指定评价指标体系。舱室空间中不存在味觉评价指标,因此在将前4种感官以及4种感官未涉及的指标综合分成5类,即视觉舒适性、触觉舒适性、听觉舒适性、嗅觉舒适性和其他舒适性。将以上5个指标设定为一级评判指标(B1~B5)。参考程远等[27]在舱室家具方面的研究,胡敏[28]对豪华游艇居住舱室舒适度研究以及刘振明[29]结合多学科对豪华游艇居住舱舒适度的研究,对邮轮舱室舒适性进行详细的划分,总结了12个影响邮轮舒适性的指标,建立了邮轮舱室舒适度指标划分,如表2所示。 在表2中,12个舒适度指标(A1~A12)按照感官接收器不同分成5类(B1~B5)。指标形式表示该指标的属性,由于不同指标数据趋向理想状态的方向不同,因此指标形式包括效益型和成本型两种,后续数据的处理将根据不同类型的指标采用不同的计算公式。在12个指标中,有3个指标可以直接通过测量方式取得精确数据A5、A6、A8,而其他9个指标需要评判专家通过打分形式取得。目前多级量表的形式被认为是一种较理想的取得主观评判数据的方式[30]。因此,采用7级量表的形式取得主观数据,如图1所示。 表2 邮轮舱室舒适性指标Table 2 Cruise cabin comfort index 图1 指标舒适程度7级量表Fig.1 7-level index of comfort 传统的TOPSIS评价方法,是一种接近理想方案分析折中解法。运用解法中的正负向理想解,并通过方案趋近于正向理想解而远离负向理想解而对方案优劣进行评判。因此,传统TOPSIS法中需要通过确定的隶属度函数获得隶属度值,但在不确定问题研究过程中,受到主观因素以及一些不确定环境影响,模糊量集的隶属度函数确定困难,难以求解精确的隶属度值或求解的隶属度值准确性较差。因此,引入粗糙集作为解决主观问题的方法。 多指标综合评价包括指标权重确立和运用指标权重进行评价两个步骤,如图2所示。 图2 评价流程Fig.2 Evaluation process 根据人的感官体验确立本研究的评价指标后(表3),按照图2所示的评价流程进行评价。按照Part 1,首先确定各指标的权重,主要包括以下步骤。 步骤1基于7级量表专家评分。针对q个评价指标(A1~Aq),将所有指标运用七级量表的形式表示,让p位专家对所列指标进行主观评价。 步骤2建立重要性矩阵。在这个步骤中,对评价专家评价结果进行汇总,形成重要性矩阵,如表3所示。 步骤3建立粗糙数矩阵。运用粗糙集的上下近似等近似公式[式(1)~式(7)]运算来处理模糊性和不确定性数据。 步骤4确定权重。确定每个指标的权重。指标权重wj计算公式为 j=1,2,…,n (14) 式(14)中:m为备选方案的数目;n为指标数目。 表3 评价专家对于评价指标重要性评价表Table 3 Evaluation table for the importance of evaluation indicators by evaluation experts 确定各评价指标的权重wj后,可按照Part 2进行Rough -TOPSIS评价模型的构建。 步骤1专家根据指标对各个方案打分。专家对于舱室舒适度相关的主观评价指标进行打分。 同时,对于确定指标,采用测量的方式获取数据。并对指标数值汇总形成评价原始数据表。 步骤2建立评价粗糙矩阵。根据式(1)~式(7),将指标数据转化为粗糙数形式,形成矩阵,用M表示,M可表示为 (15) 步骤3确定正负理想解。根据矩阵M确定正理想解x+和负理想解x-。 x+={x+(1),x+(2),…,x+(j)} (16) x-={x-(1),x-(2),…,x-(j)} (17) 式中: 步骤4计算偏差系数。偏差系数是描述一个粗糙数与正理想解与负理想解之间的距离的度量。它也是一个粗糙数,公式为 (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) 步骤5对偏差系数进行归一化处理,公式为 (28) (29) (30) (31) 得到正态偏差矩阵d+′和d-′。 (32) (33) (34) (35) (36) (37) 最后根据式(38)计算各方案的CI并进行排序。CI表示该备选方案与正理想解的贴合程度,排序结果贴近度CI越大,表示该方案越优,方案之间排序可得。 (38) 研究中运用Rough-TOPSIS法对3个不同邮轮的同等级邮轮舱室进行评价并排序。3个舱室分别记录为舱室一、舱室二、舱室三。 邀请4位专家针对12个评价指标进行重要程度评分,将所有的指标运用7级量表的形式表示,其原始数据如表4所示。 表4 专家对案例中涉及指标重要性评价表Table 4 Expert evaluation of the importance of the indicators involved in the case 则根据上述公式有 则可得 将所有数据按照上述方法形成粗糙数矩阵后,根据式(14)可以求出权重wj,其结果如表5所示。 确定权重后,根据Part 2的方法首先确定3个评价舱室各指标的评价原始指标值。各指标中,A5振动、A6空气流速和A8噪声为测量数据,分别由振动分析仪、风速仪和声级计测量。由于决策专家共有6人,因此仪器测量数据取得了间隔时段的6次样本。再利用邀请6位专家根据舱室情况对剩余指标打分。以舱室一为例,仪器测量和专家评定原始数据如表6所示。 根据式(1)~式(7)将其转化为粗糙数形式。同理,将舱室二和舱室三的评定指标转换粗糙数形式,构建决策矩阵M,如表7所示。 根据成本型和效益性指标不同的判定方式,可确定正理想解x+和负理想解x-,如表8所示。 根据式(18)~式(25)计算偏差系数,建立偏差系数矩阵d+和d-,如表9和表10所示。 表5 各指标权重值Table 5 Weight values of each index 表6 舱室一评定指标原始值Table 6 Original value of cabin 1 evaluation index 表7 各舱室粗糙数形式矩阵MTable 7 Rough number matrix M of each cabin 表8 正理想解x+和负理想解x-的值Table 8 Values of positive and negative ideal solutions x+ and x- 根据式(28)~式(31),对偏差系数进行归一化处理,得到正态偏差矩阵d+′和d-′,分别用表11和表12表示正态偏差矩阵d+′和d-′。 表9 偏差系数矩阵d+Table 9 Deviation coefficient matrix d+ 表10 偏差系数矩阵d-Table 10 Deviation coefficient matrix d- 表11 正态偏差矩阵d+′Table 11 Normal deviation matrix d+′ CI越大,说明该舱室与正理想解的贴合度越高,舱室越优。由表可知,舱室二CI最大,与正理想解的贴合度最高,舱室二最优。 表12 正态偏差矩阵d-′Table 12 Normal deviation matrix d- ′ 表和CI值 在一般评价当中,评判专家趋向一般趋近于中立态度,故乐观性系数α一般取0.5。从图3可以看出,在α取值为0.1、0.3、0.5、0.7和0.9时,舱室一的评价结果始终优于其他2个,而且3个舱室的评价顺序始终为舱室一、舱室二、舱室三。舱室一的优势随着α的增加而逐渐明显,而舱室二和舱室三的差距则随着α的增加而减小。 图3 不同α值时方案敏感性比较图Fig.3 Sensitivity comparison of schemes with different α values 将Rough-TOPSIS法与传统的TOPSIS法以及常见的运用对称三角模糊数的Fuzzy-TOPSIS进行对比。在计算指标权重时,3种方法权重值范围如表14所示。尽管对称三角模糊数能够在一定程度上使确定数据形成区间范围,但该范围过分笼统。如对于指标A1,根据专家评判,其重要性权重均值为4,对应三角模糊数范围为[3,5]。事实上,该对称的范围很难反映出评判专家的真实需求。而粗糙数时基于粗糙集思想而计算球的,能够更好地表现决策者的主观意愿。 由表15可见,通过3种评价方式对相同的评价对象的评价,当α取0.5时,Rough-TOPSIS和Fuzzy-TOPSIS的结果一致,而传统的TOPSIS法在评价结果出现了不同。舱室设计评价排序的差异,主要是由于TOPSIS法具有主观性影响,而Rough-TOPSIS和Fuzzy-TOPSIS对指标数值模糊化处理,减少了主观性的影响。通过对实验船舱的比较,确定实验船舱中舒适度最优的舱室。也验证了该方法的有效性。 表14 各方法指标权重值Table 14 Index weight value of each method 表15 各方法评价结果排序对比Table 15 Rank comparison of evaluation results of each method 以邮轮舱室舒适性为研究对象,运用TOPSIS法对邮轮舱室舒适性进行研究,参考近几年的文献资料,从感官舒适性的角度出发,总结出12个影响邮轮舱室舒适性的指标因素,针对TOPSIS法权重具有主观性问题,采用粗糙集理论求出各指标的权重。通过对传统TOPSIS法、Rough-TOPSIS法以及Fuzzy-TOPSIS法3种评价方式对相同的评价对象的评价,验证了Rough-TOPSIS法对邮轮舱室舒适性评价的科学性与有效性。运用Rough-TOPSIS理论对3个邮轮舱室的舒适性设计舱室进行比较评价,最终确定舱室一为最优舱室,对于邮轮舱室舒适性设计和评价具有一定的指导意义。 Rough-TOPSIS评价方法为邮轮舱室舒适性的研究提供了新的研究思路,为以后邮轮舱室舒适性的设计以及舱室舒适度评价提供新的参考依据。 Rough-TOPSIS评价方法运用粗糙集理论求指标权重,能够减少主观评价带来的偏差;同时,Rough-TOPSIS法对问题样本数量没有限制,不仅适用于少样本问题,同样适用于多样本问题;不仅如此,Rough-TOPSIS评价方法对结果有较为直接的几何表达,对以后实际工程的评价提供了新的研究方法。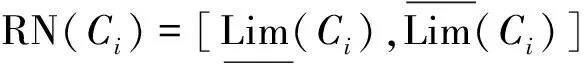
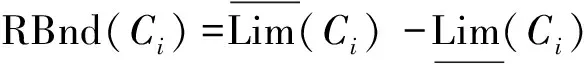
1.2 TOPSIS法
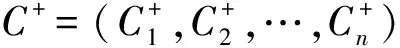

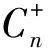

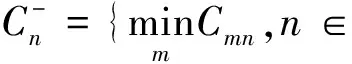
2 评价指标的确定


3 基于Rough-TOPSIS的评价模型

3.1 基于Rough set 的权重确定
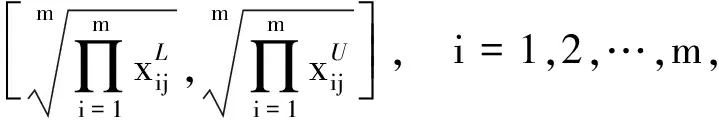
3.2 构建Rough -TOPSIS评价模型

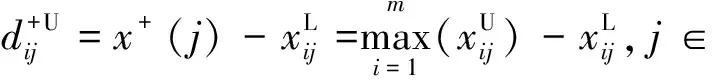




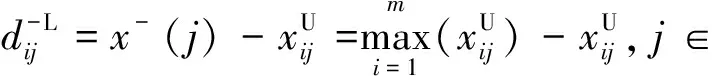

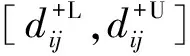

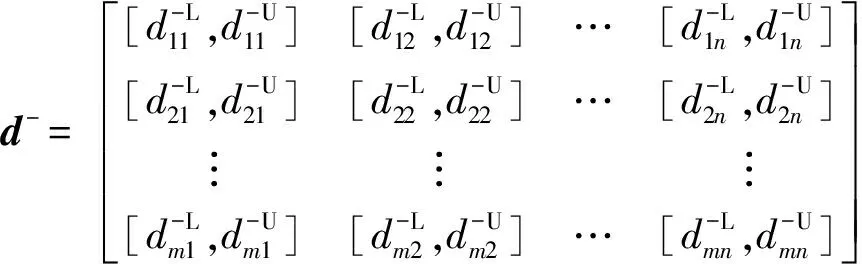
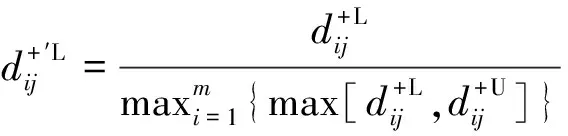

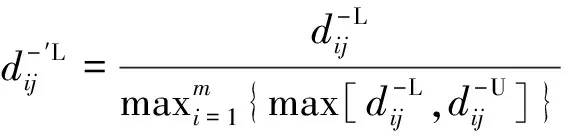
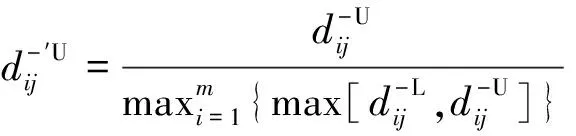

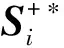

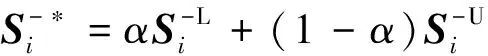

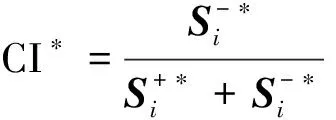
4 评价案例
4.1 基于Rough-TOPSIS法的决策
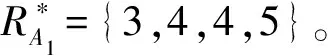

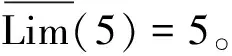



4.2 方案敏感性

4.3 方案有效性对比


5 结论

