水介质初始参数设置对水下爆炸载荷的影响*

郑永辉，魏继锋

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

随着数值计算方法的进步和计算能力的提升，数值仿真技术为解决水下爆炸机理分析、结构响应机制规律揭示等科学技术难题提供了有力的手段。在水下爆炸数值仿真研究中，研究人员已对水介质状态方程、人工黏性系数、网格密度等影响计算精度的因素开展了较为细致的探讨。

在进行水下爆炸问题计算时，需设定水介质的初始参数以设置流场初始压力。已有研究中，大多采用以下两种方式：一是认为水介质密度变化很小，可忽略不计，仅通过改变内能设置流场初始压力；二是认为流体静压力的增大导致水的密度增大，仅通过调整比容来设置初始压力。当采用前一种方式时，冲击波超压峰值随水深的增大略有减小，后一种方式下的变化趋势则相反。可以看出，初始参数的设置方式会带来水下爆炸载荷计算结果的差异，而对此的细致分析尚未见报道。

除直接设置水介质初始参数外，也可通过施加重力、采用程序提供的特定功能等方式实现流场压力初始化。这些方式简化了操作，但程序仍需提供水介质的初始参数使其具有一定的压力。以LSDYNA 提供的关键字INITIAL_EOS_ALE 为例，其说明文档指出，程序将采用一种迭代方法根据用户提供的压力计算介质的初始内能和比容。简而言之，该类方法其本质上也是对水介质的初始参数进行设置。

水介质初始参数设置本质上是对水介质参数随水深变化的规律的反映。本文中将首先从常用的状态方程中选定符合参考状态时参数的水介质状态方程；然后从热力学角度分析现有两种设置方式对应的热力学过程，并给出第3 种参数设置方式，同时以关键字INITIAL_EOS_ALE 为例，对程序给出的初始化结果进行分析；随后采用LS-DYNA 程序进行一维球形装药水下爆炸仿真研究，细致分析前三种初始参数设置方式对水下爆炸载荷特性的影响，并与已有研究成果进行对比；最后确定适当的初始参数设置方式。

1 水介质状态方程

数值仿真软件中常见的水介质状态方程为Mie-Grüneisen 状态方程和Polynomial 状态方程。Mie-Grüneisen 状态方程以冲击绝热线作为参考线，最终形式为：

式中：、、、、、和均为状态方程系数，e为质量内能增量，、、、、、和均为状态方程系数，、、、、、和均为状态方程系数。

与Mie-Grüneisen 状态方程类似，式（2）～（3）也存在与实际压力不符的问题。式（4）在=时，可满足= 0，e= 0 以及=。因此，宜选择Polynomial 状态方程式（4）作为水介质状态方程，具体参数见表1。

表1 水介质状态方程参数Table 1 EOS parameters of water

2 初始参数设置

2.1 设置方式及状态参数变化

根据水介质状态方程，设置初始压力时可改变参量和e。现今大多数仿真研究是通过改变e（方式Ⅰ）来进行流场初始压力设置。从热学角度看，方式Ⅰ中不同水深下的水介质参数按等容过程（d=0）变化，此时外界做功为零，流场的内能增量全部由外界传导的热量提供（d= d）。这表明采用方式Ⅰ时，流体静压力的增大单纯源于外界传热，与重力等外力做功等因素无关，这与实际深水环境以及加压模拟深水环境严重不符。

少数研究人员通过调整（方式Ⅱ）来进行初始压力设置。此时，内能变化为零（d= 0），即等内能形式，外界对流体做功与外界向流体传导的热量之和为零（d= d-d= 0），水介质被压缩后向外放出热量。为分析温度变化趋势，引入含温度的内能表达式：

式中：= 273 K。当0 ≤≤ 0.025 时，随的增大而逐渐增大（见图1）。在实际深水环境中，随着水深的增大，水温逐渐减小；在通过加压构造的模拟深水环境中，水温与环境温度基本相同，即温度可认为保持不变。因此，从温度变化趋势的角度来看，方式Ⅱ与实际情况有一定的差距。

热力学研究结果表明，温度到处相同是重力场的热平衡条件。据此，本文中提出第3 种初始参数设置方式，即假设水介质参数随水深按照等温过程（d= 0，方式Ⅲ）变化。对于该方式，Δ= 0，将式（5）代入式（4），可得等温过程对应的状态方程。显然，对于实际深水环境，方式Ⅲ只是一种粗糙的近似，不过理论上优于方式Ⅰ和方式Ⅱ；对于模拟深水爆炸试验，近似程度较高。

除上述设置方式外，数值仿真软件往往也具备根据重力和水深信息或者设定的流体静压力计算水介质初始参数的功能，只是用户往往无法直接获知其遵循的规律。现以关键字INITIAL_EOS_ALE 为例，通过读取不同水深下的流场压力初始化结果来初步了解LS-DYNA 程序中和e随水深的变化规律（方式Ⅳ），结果如图1 所示，可以看出，方式Ⅳ对应的热力学过程接近方式Ⅱ。

图1 中给出了4 种设置方式在不同水深条件时的压缩比、内能增量e和温度变化Δ的计算结果。方式Ⅱ和方式Ⅳ的计算结果几乎重合，二者均与方式Ⅲ较接近；方式Ⅰ的计算结果与其他3 种相去甚远。采用方式Ⅱ、Ⅲ、Ⅳ时，随水深增加而增大；采用方式Ⅰ时则始终为零；在同一水深处，的值从小到大依次为：方式Ⅰ、方式Ⅳ、方式Ⅱ、方式Ⅲ。采用方式Ⅰ和方式Ⅳ时，e随水深增加而增大，采用方式Ⅱ时e始终为零，采用方式Ⅲ时e随水深的增加而减小；在同一水深处，e的值从小到大依次为：方式Ⅲ、方式Ⅱ、方式Ⅳ、方式Ⅰ。采用方式Ⅰ、方式Ⅱ和方式Ⅳ时，Δ随水深增加而增大；采用方式Ⅲ时Δ始终为零；在同一水深处，Δ的值从小到大依次为：方式Ⅲ、方式Ⅱ、方式Ⅳ、方式Ⅰ。

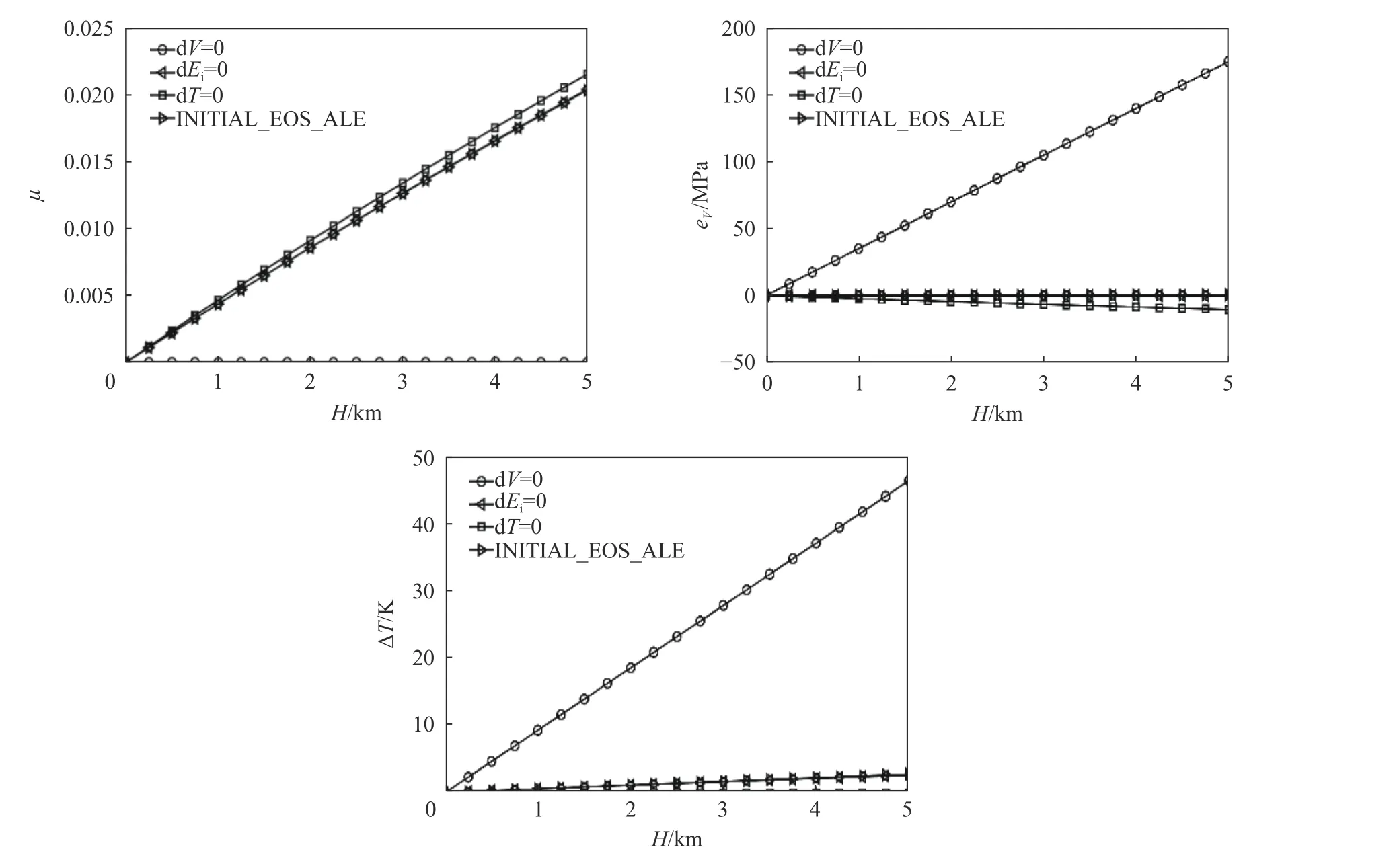
图1 不同设置方式下的μ、eV 和ΔT 值Fig. 1 Values of μ, eV and ΔT in different setting modes

2.2 流体可压缩性

流体的可压缩性决定流体内微弱扰动波的传播速度，即流体内的声音传播速度，因此常用声速来表示流体的可压缩性。声速的表达式为：

图2 中给出了4 种设置方式在不同水深条件时的声速。从图2 中可以看出，随着水深的增大，4 种方式下的水介质声速逐渐增大，即可压缩性均出现减弱，但减弱幅度不同，由小到大的排序为：方式Ⅰ、方式Ⅳ、方式Ⅱ、方式Ⅲ。可见，声速的变化与压缩比的变化情形一致。

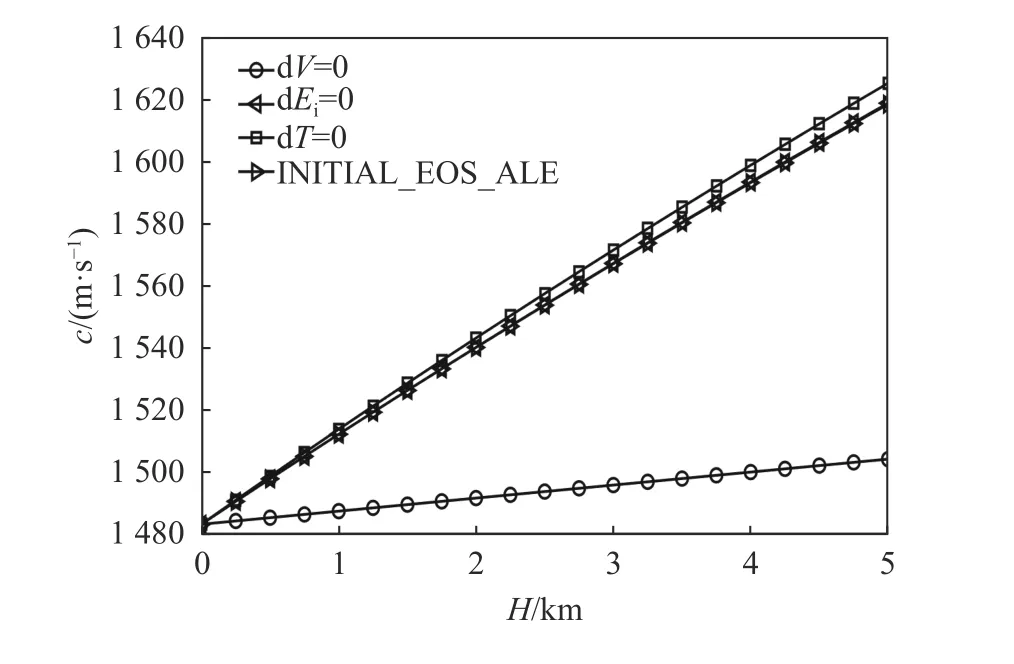
图2 不同设置方式下的声速变化Fig. 2 Acoustic velocity in different modes

3 初始参数设置对水下爆炸载荷的影响

3.1 数值仿真模型

建立了一维球对称水下爆炸数值仿真模型，并应用LS-DYNA 数值仿真软件进行计算。其中，炸药采用MAT_HIGH_EXPLOSIVE_BURN 材料模型以及JWL 状态方程，参数取自文献[17]。水介质的状态方程采用式（4），参数在表1 中列出。

炸药选用1 kg TNT，水深范围0 ～ 5 km，由于方式Ⅱ和方式Ⅳ对应的初始参数极为接近，因此只对比前3 种方式，各自对应的和e值取自图1。为保证计算精度，网格尺寸为装药半径的1/100；为减小边界反射冲击波对气泡脉动的影响，水域半径取237.2 m，大于水深为0 m 时声波在一个脉动周期内传播距离的1/2。

3.2 冲击波载荷特性

选取水深为5 km，爆距= 55（为装药半径），计算得到了3 种方式下的冲击波压力-时间曲线，如图3 所示，对应的冲击波到达时间、超压峰值Δ和正压持续时间列于表2 中。可以看出，3 条曲线并不完全重合，除方式Ⅰ外，其他2 种方式的仿真结果相差较小；方式Ⅲ、Ⅱ、Ⅰ的及值依次减小，而Δ依次增大。该规律与流体可压缩性结果基本一致，即流体可压缩性越弱，冲击波到达时间越短，冲击波超压峰值越大，正压持续时间越短。

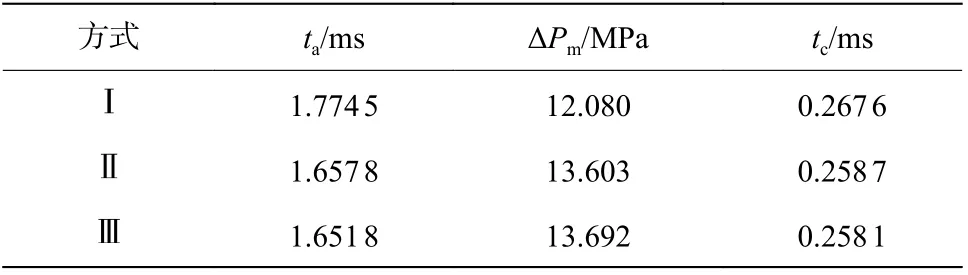
表2 H =5 km 及 R =55R0 时3 种方式下的 ta 、 Δ Pm 及tcTable 2 Values of ta , Δ Pm and tc in three modes when H =5 km andR=55R0

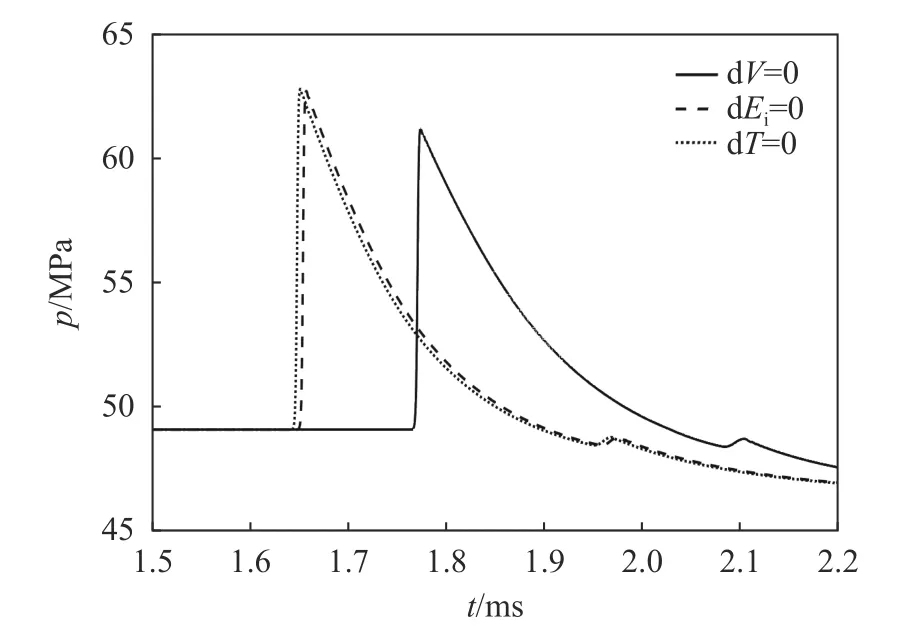
图3 H=5 km 及R=55R0 时3 种方式下的冲击波压力-时间曲线Fig. 3 Shock wave pressure-time curves in three modes when H=5 km and R=55R0

图4 中给出了= 55时3 种设置方式在不同水深下获得的冲击波超压峰值、冲量和能流密度，其中，和分别由下式给出；

图4 R=55R0 时不同水深下3 种方式所对应的冲击波载荷参数Fig. 4 Values of shock wave load in three modes when R=55R0

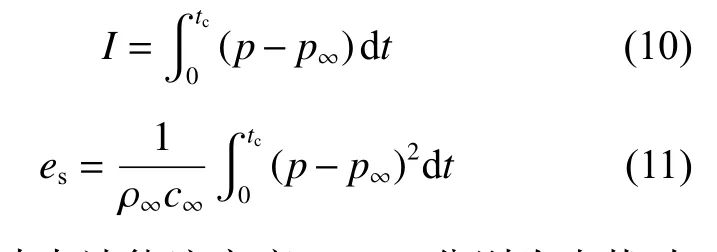
式中：为冲击波能流密度，ρ、分别为未扰动流体的密度和声速，为便于比较，统一取ρ= ρ=1 000 kg/m，== 1 483.2 m/s。

表3 中给出了冲击波载荷参数在5 km 水深处相对于0 m 的变化幅度。可以看出，随着水深的增大，采用方式Ⅰ时Δ逐渐减小，其他2 种方式则逐渐增大，且变化幅度略大于方式Ⅰ。对于和，3 种方式给出的仿真结果均随水深的增大而减小，方式Ⅱ和Ⅲ的变化幅度略小于方式Ⅰ。

表3 冲击波载荷在5 km 水深处相对于0 m 的变化幅度Table 3 Changing amplitudes of shock wave load when depth changes from 0 m to 5 km

3.3 气泡脉动特性

分析=5 km 时3 种设置方式下气泡的脉动曲线，如图5 所示，相应的气泡最大半径和第1 次脉动周期列于表4。可以看出，除方式Ⅰ外，其余两条曲线基本重合；方式Ⅲ、方式Ⅱ、方式Ⅰ对应的和依次增大。显然，该规律与水介质压缩比的变化一致。由于气泡脉动与水介质的惯性密切相关，当体积不变时，水介质密度的增大导致其惯性增大，在密度变化较小时惯性增幅有限，因此，3 种方式下气泡脉动曲线的差别并不明显。

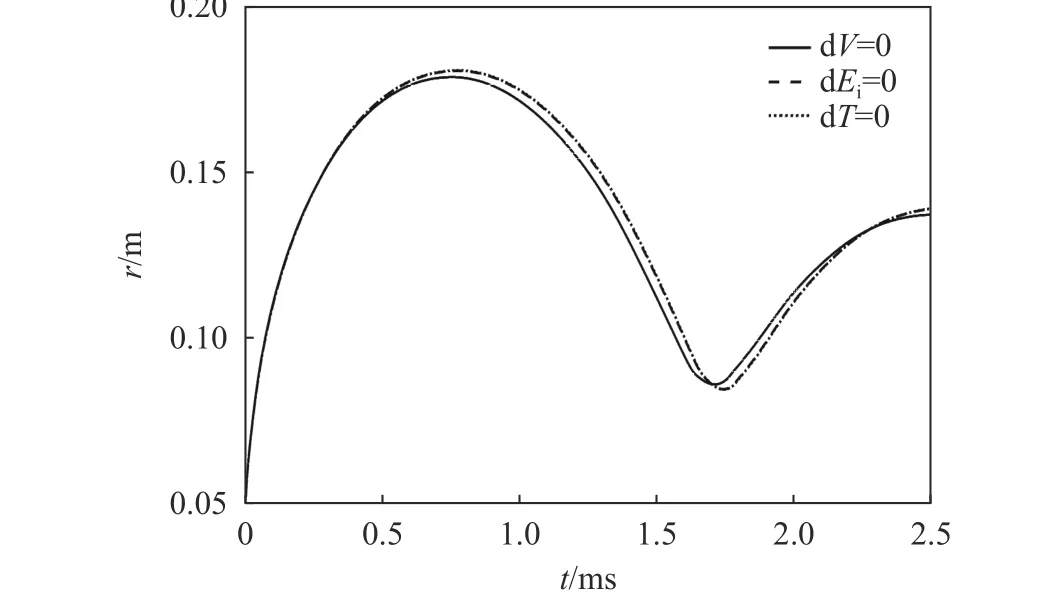
图5 H=5 km 时3 种方式下气泡的半径-时间曲线Fig. 5 Bubble radius-time curves in three modes when H=5 km

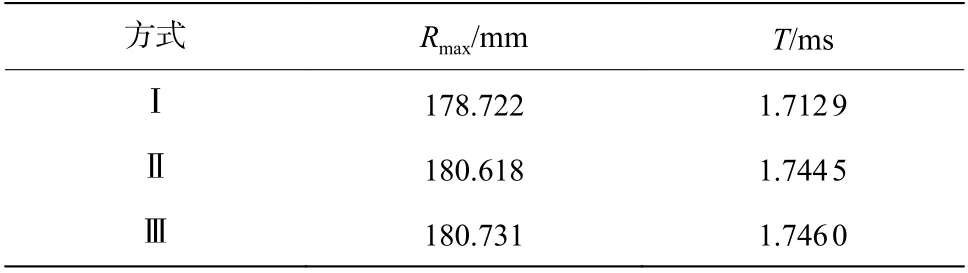
表4 H =5 km 时3 种方式下对应的 R max 和TTable 4 Values of R max and T in three modes whenH=5 km

4 对比分析

4.1 冲击波载荷对比分析

自20 世纪60 年代起，研究人员开展了较多的水深对冲击波载荷特性影响的研究。Baum 等在模拟深水爆炸容器中进行了深水爆炸试验，当1 ＜/＜ 7 时，Δ在0 ～ 4 km 的模拟水深范围内基本保持不变。Vanzant 等给出了14.75 g Pentolite 炸药在更大爆距范围内的试验结果，本文对其试验数据进行了线性拟合，结果表明，Δ随水深的增大而略有增大，且在较大爆距处的变化更明显，如图6 所示。钟帅等开展了0～150 m 模拟水深水下爆炸试验，指出Δ也随水深增大而略有增加。Slifko、Xiao 等也进行了类似研究，不过试验在大洋中进行，爆源和测点并不位于同一深度，而且爆距较大，与本文分析工况不符。

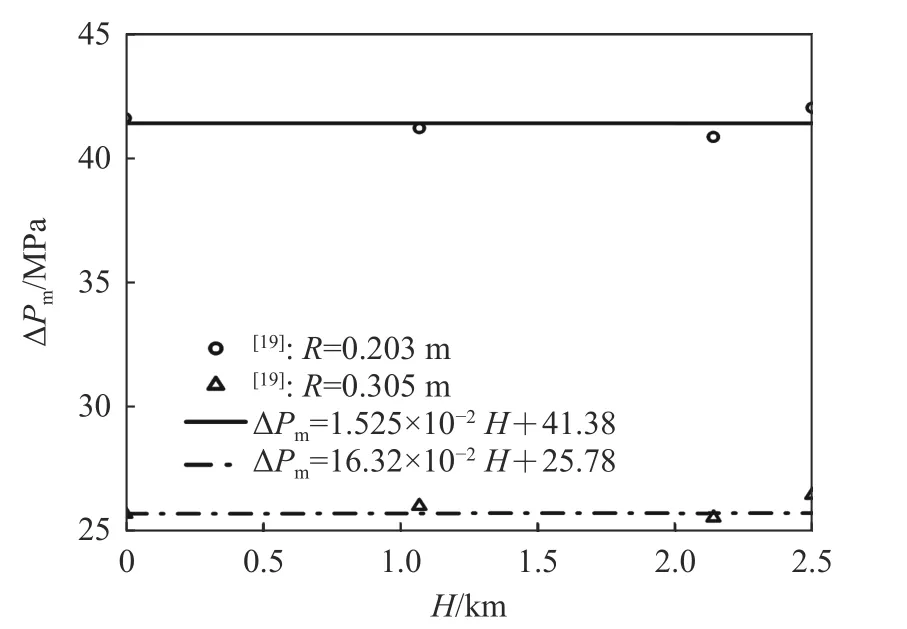
图6 Vanzant 等[19]的试验结果及线性拟合曲线Fig. 6 Test results from Vanzant et al[19] and linear fitting results

理论上，Baum 等从相似性和量纲理论出发，在浅水经验公式的基础上，给出了考虑流体静压力时Δ的计算式：

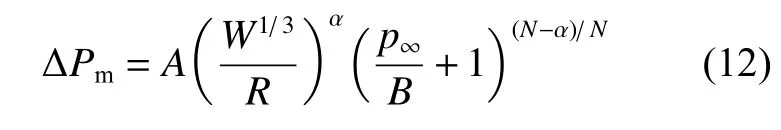
式中：和α 为常数，当6 ≤/＜ 12 时，=44.1 MPa，α = 1.5；当12 ≤/＜ 240 时，=52.4 MPa，α = 1.13；= 304.9 MPa 为Tait 状态方程中的常数；为几何指数，对于球面冲击波，= 3。

式（12）表明，Δ随水深的增大而缓慢增大；同时随着爆距的增大，α 逐渐减小，流体静压力对Δ的影响逐渐增大。

从前述研究中可以看到，随着水深的增大，采用方式Ⅱ和方式Ⅲ时Δ会逐渐增大。从图7 中可以看到，5 km 水深条件下当7≤≤ 65时，随着爆距的增大，水深对Δ的影响也在逐渐增大。图8为= 5 km 时3 种方式下Δ计算结果相对于式（12）的误差。综合来看，采用方式Ⅱ和方式Ⅲ获得的计算结果与试验值及理论值均较为吻合，方式Ⅲ的相对误差更小。

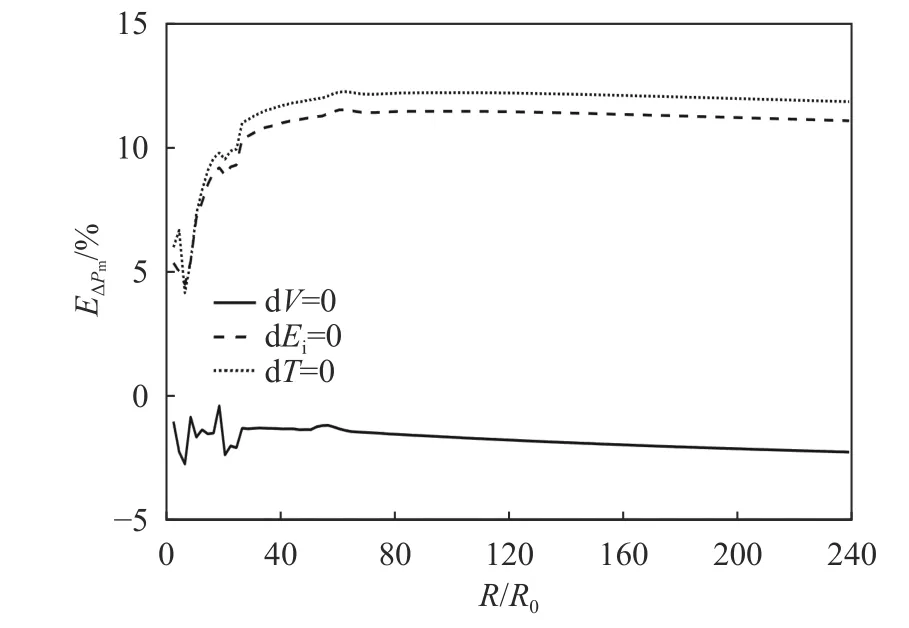
图7 ΔPm 在5 km 水深处相对于在0 m 处的变化幅度Fig. 7 Changing amplitudes of ΔPm when depth changes from 0 m to 5 km

图8 H=5 km 时ΔPm 相对于计算式(8)的误差Fig. 8 Relative errors of ΔPm between simulation results and calculation formulas when H=5 km

4.2 气泡脉动参数对比分析

Cole基于不可压缩理论模型推导了和与水深和装药量的关系，Swift 等基于试验数据给出了计算气泡脉动参数的经验公式：

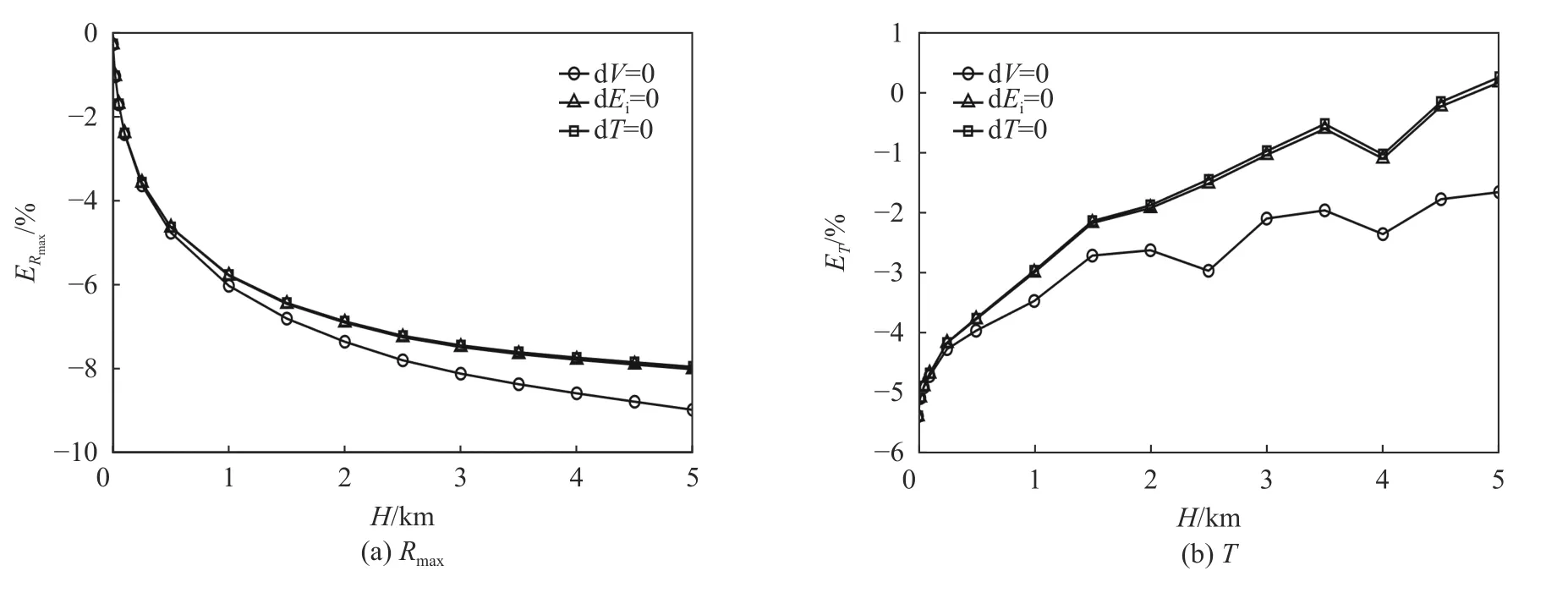
图9 气泡脉动参数相对于经验值的误差Fig. 9 Relative errors of Rmax and T between simulation and empirical formula

4.3 设置方式合理性探讨

从热力学角度看，2.1 节中已指出，采用方式Ⅰ时，流体静压力的升高单纯由外界传热引起，这与真实情形不符；采用方式Ⅱ和方式Ⅳ时，温度随水深的增大而略有增大，与实际情况有一定差距。采用方式Ⅲ时，水介质温度不随水深变化，与模拟深水试验条件吻合，与实际深水环境的吻合性较方式Ⅰ、Ⅱ和Ⅳ要好。从与已有成果的对比分析看，方式Ⅱ、Ⅲ的结果与已有成果吻合较好；相较而言，采用方式Ⅲ时载荷值的相对误差最小。综上分析认为，初始参数设置宜选用方式Ⅲ，方式Ⅱ和方式Ⅳ次之，在讨论水深影响时不建议选用方式Ⅰ。

5 结 论

分析了4 种水介质初始参数设置方式对应的热力学过程，并采用有限元数值仿真方法，深入探讨了初始参数设置方式对水下爆炸载荷特性的影响，并与相关试验与理论研究成果进行了对比分析，主要结论如下。

（1）根据参考状态下水介质参数，选择式（4）形式的状态方程作为水介质状态方程；其他常用状态方程均忽略了参考压力项，无法满足参考状态下的水介质参数。

（2）仅改变水介质内能增量e，流体压力源于外界传热，与实际环境不符；仅改变压缩比时，水介质温度随水深的增大而略有增加；LS-DYNA 中INITIAL_EOS_ALE 关键字给出的初始参数计算结果与等内能假定非常接近；与上述3 种方式相比，本文提出的等温假定更符合真实深水环境以及模拟深水试验条件。

（3）按等内能假定和等温假定设置初始压力时，水下爆炸载荷特性结果接近，与相关试验与理论研究成果吻合良好；综合分析实际深水环境以及模拟深水试验条件，在数值仿真计算的初始压力设置时，宜选用本文提出的水介质参数等温变化假定。