传感器切换代价约束下的调度方法

李召瑞，安 雷，吉 兵，朱世磊

（陆军工程大学 石家庄校区，河北 石家庄 050051）

0 引 言

传感器调度主要通过有针对性地分配传感器资源及探测时间区间，以达到提高目标跟踪精度、降低使用代价等目的。在传感器目标跟踪的实际应用中，调度信号延迟、伺服系统工作驻留、跟踪信息转交等因素频繁地切换会严重影响目标跟踪效能。在跟踪精度的同时，为降低切换频次，文献[2]将交接次数阈值代入到调度方案求解当中，但只能获得次优解；文献[3]为应对相控阵雷达跟踪中存在的时延问题，引入调度代价以确保任务优先级，但可操作性不强，容易丢失最优解；文献[4]则基于最大切换次数求解多基地雷达系统最优调度序列，但未考虑工作时长因素，仍然存在缺陷；文献[5]基于固定工作时长约束研究传感器调度方法，规定传感器只要达到工作时长就进行切换，没有考虑代价因素，与实际情况不符；相比之下，文献[6-7]中调度时刻由工作时长和代价函数共同决定，方法更加贴近实际。

针对上述问题，本文以多传感器跟踪多目标为应用场景，基于最小工作时长，提出一种以传感器切换代价为约束条件的长时调度方法。首先，基于POMDP建立多传感器系统跟踪多目标场景下的调度模型；然后，将交互式多模型算法（IMM）与模糊积分粒子滤波算法（FQPF）相结合，并以后验克拉美罗下界（PCRLB）为衡量指标，提出长时跟踪精度的预测方法，当传感器达到最小工作时长后，再根据跟踪精度预测结果来决策是否进行切换；最后，通过仿真实验验证调度模型和调度方法的有效性。

1 问题的数学描述

1.1 调度动作

1.2 系统状态模型及转移函数

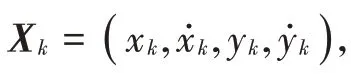
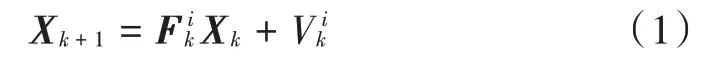
1.3 系统观测模型

1.4 目标优化函数

充分考虑不同传感器功能的差异性，将传感器的最小工作时长设为φ∈{ },,…,φ。假设其中传感器在时刻已工作满φ时长，则此时依据目标优化函数决策是否进行切换，若仍然调度进行观测，则在+1时刻继续决策；若时刻选择调度传感器(≠)，则该传感器必须工作满φ时长，直至+φ时刻重新决策是否切换传感器。

在此基础上，构建目标优化函数：

2 切换代价控制下的传感器调度方法

2.1 IMM-FQPF算法

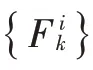
2.1.1 初始数据交互

2.1.2 模型滤波估计

2.1.3 模型概率更新

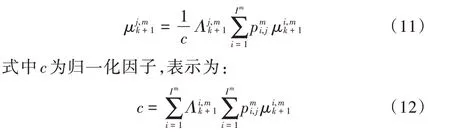
2.1.4 数据估计融合

根据目标在各模型跟踪下的状态、协方差及对应的模型概率，获得+1时刻的目标的运动状态及其协方差矩阵：

通过IMM-FQPF算法可以有效改善目标跟踪能力，便于长期跟踪精度的准确预测。

2.2 基于PCRLB的长时目标跟踪精度的预测方法

PCRLB是随机向量̂的Fisher信息矩阵的逆矩阵，它可以在目标跟踪中仅依据当前先验信息，预测下一步或多步时刻内未知状态的估计性能边界，常作为跟踪精度的衡量指标，其详细推导过程见文献[13]。在PCRLB的基础上结合IMM-FQPF算法，提出长时跟踪精度的预测方法。

1）初始化

4）计算目标状态转移先验概率密度函数

依据文献[15]，目标的状态转移先验概率密度函数为：

2.3 调度方法流程

3 仿真实验

3.1 对比不同策略，分析调度方法性能

在仿真中，为验证本文提出方法的有效性，同时选取无时长约束调度策略（Non Time Constrained Scheduling Policy，NTCSP）以及固定时长约束调度策略（Fixed Time Scheduling Policy，FTSP）进行对比，三种方法的目标跟踪精度对比结果如图1所示。

由图1可看出，阈值分别取40，50，60时，将本文方法与NTCSP、FTSP所得目标跟踪精度进行对比，目标跟踪精度的值用协方差矩阵的迹来表示。由于三种方法本质上都是调度满足跟踪精度阈值的误差最小的传感器进行跟踪，所以基本都能满足阈值要求。但在目标跟踪中，传感器的切换次数越多，产生的切换代价越大，而本文的优化目标是利用更小的切换代价，获得更高的跟踪精度，所以采取阈值与平均跟踪精度的差除以切换次数的数值作为指标，衡量不同方法在目标跟踪中的实际效能。为此，将三类方法在跟踪过程中的平均跟踪精度、传感器切换次数及跟踪效能指标进行对比，结果如表1所示。

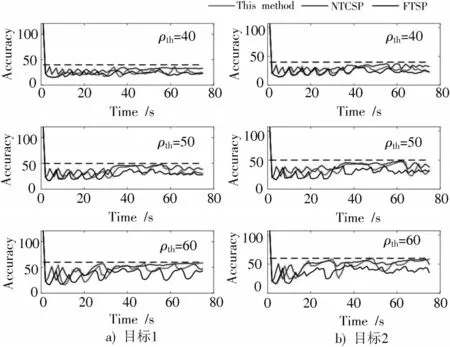
图1 不同阈值条件下的目标跟踪精度

表1 不同阈值条件下的目标跟踪效能对比

从表1中可知：FTSP的平均跟踪精度要略低于本文方法，但由于其规定传感器工作满固定时长后，必须切换其他传感器进行跟踪，导致切换次数明显偏高；而NTCSP不考虑工作时长约束，每一时刻都进行决策，切换次数最高。所以，在3个阈值条件下比较跟踪效能指标，所提方法明显优于NTCSP和FTSP。

在本节仿真条件下，利用所提方法跟踪目标得到的运动轨迹及调度序列如图2、图3所示（=50）。

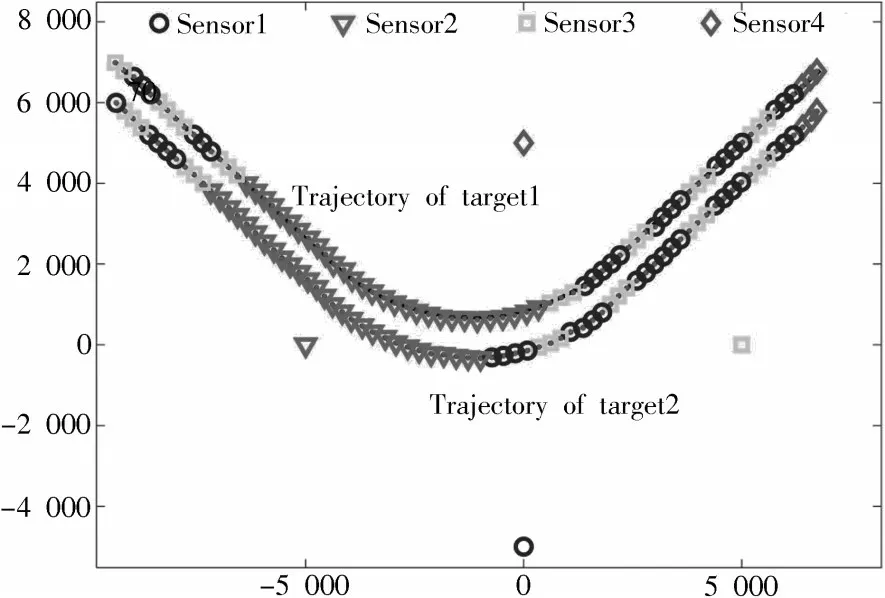
图2 目标运动轨迹

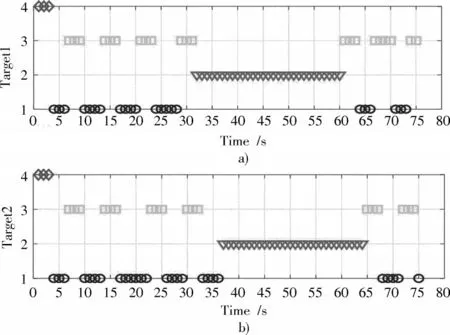
图3 传感器调度序列

3.2 阈值选取对目标跟踪效能的影响

从3.1节仿真实验可以看出，不同阈值条件下的传感器系统目标跟踪精度和切换次数存在显著差异。为进一步分析阈值选取在本文所提方法中对目标跟踪效能的影响，在[10，90]区间内间隔一共选取81个阈值进行200次蒙特卡洛仿真实验，其余参数设置不变。不同阈值下的平均跟踪精度结果如图4所示。由图4可知：当阈值小于40时，所提方法的目标跟踪精度受跟踪算法性能的限制，将会稳定保持在算法精度的最小值附近波动；反之，阈值设置的过大，所有的传感器都能满足要求，将会减弱阈值对跟踪精度的限制作用，而且由于跟踪精度会随着时间的推移保持稳定，所以随着阈值的不断增大，平均跟踪精度将逐渐趋向于跟踪算法精度的均值。

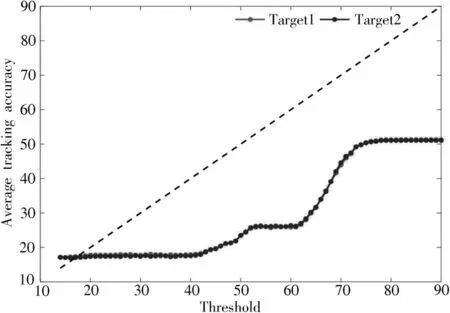
图4 不同阈值下的平均跟踪精度

根据目标函数的要求，在不考虑辐射代价的前提下，要利用更低的切换代价获得最佳的跟踪精度，不同阈值下满足其精度要求的时长曲线如图5所示。由图5可知，当阈值过低时，受跟踪算法性能的限制，每轮仿真时间内不能达到跟踪精度阈值要求的时间较大（当＞24时，满足阈值要求的时间等于74 s）。

图5 不同阈值下满足跟踪精度阈值要求的时长

不同阈值下的传感器切换次数如图6所示，当阈值过高时，一方面急剧增加的传感器切换次数会带来过高的切换代价，影响跟踪性能；另一方面过高阈值所带来的跟踪精度上升问题，也会使得目标跟踪失去意义。阈值小于40时，阈值的变化对传感器跟踪精度的影响较小，在满足阈值的前提下，基于降低调度代价的目的，会促使传感器切换次数保持在较低水平。所以，为保持更佳的目标跟踪效能，阈值建议在（24，40）区间内选取。

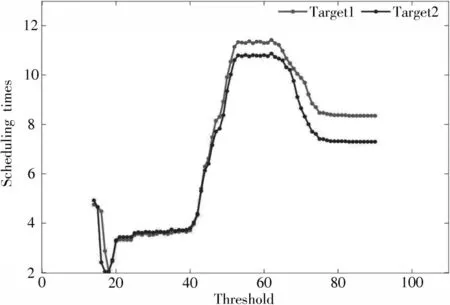
图6 不同阈值下的传感器切换次数

4 结 语

本文以多传感器跟踪多目标为应用场景，引入最小工作时长，提出一种切换代价约束下的传感器调度方法。该方法在保证目标跟踪精度的同时，可有效兼顾传感器切换代价，跟踪效果稳定，可依据实际任务需求，通过阈值对跟踪精度进行有效控制，进而减少不必要的调度，基本实现了利用更少的切换代价获得较好跟踪精度的目标。仿真实验结果表明，相比于NTCSP和FTSP，本文方法在满足跟踪精度阈值要求的同时，显著降低了传感器切换次数，能够有效克服切换代价对目标跟踪的影响，跟踪效能更优。