服务水平约束下多级供应链网络优化研究
何玲辉 (浙江育英职业技术学院,浙江 杭州 310018)
随着技术的发展和消费者需求品类日益多样化,供应链上企业之间的关联越来越重要,供应链上商品的流向和流量对整个供应链影响越来越大,最直接的影响就是整个供应链的成本变化和供应服务水平。本文以A企业所处的供应链做为研究对象,研究在以总运作成本最低作为决策总目标的情况下,不同客户端服务水平和不同的总仓到配送中心的服务水平情况下的供应链系统较佳决策方案。本文的研究不仅在于完善与丰富供应链优化的基础理论,而且为实践提供理论支持和依据,有助于解决供应链企业所面临的实际问题,为企业决策提供参考。
1 文献综述
对于供应链优化研究,大多数学者着眼于供应链节点——配送中心选址优化。黄丽霞引入免疫算法,选用MATLAB/APP作为研究平台,建立了相应的数学模型解决配送中心优化选址问题。沈俊宇针对冷链物流的特点及对国计民生的重大意义,对一级配送中心网络和二级配送中心冷链网络的配送中心选址问题进行了优化研究。王卫红用模糊综合评价法对农村电商配送中心选址问题进行了探讨。武方方基于大数据背景,从大感知数据、大交易数据、大交互数据角度对物流配送中心选址进行了优化研究;陈刚以军民融合作为研究背景,探讨了无人机配送中心选址问题。袁群基于不同选址方法对配送中心选址进行了研究。
有学者以供应链系统为研究对象进行研究。Chen和Lee以多级供应链为研究对象,对多级供应链的多目标问题进行了优化研究;赵志刚研究了基于回购契约的供应链协调模型。陈一鸣等(2020)用补偿模型来研究供应链最优协调策略。何玲辉从服务总成本和服务水平两方面均衡研究了供应链网络的优化问题,为企业决策提供了思路。
从以往的研究成果来看,国内外的学者对物流节点的选址研究比较多,很大一部分学者是用一些数学方法来解决供应链节点的选址问题。也有一些学者注意到供应链成本最小化和物流运输或者配送里程最小的综合问题,这些研究构成了本文的研究基础。但是怎样更有效地占领市场或者开拓市场,仅仅关注自己供应链运作成本最小是不够的,同时也要考虑供应链服务水平和顾客满意度。这方面文献不多,是本文研究的对象。
2 研究设计
2.1 分析框架
复杂的供应链网络的优化和设计一般是利用线性规划的数学模型转换成计算机程序来求出最优方案。本文首先建立相应的数学模型,然后采用供应链软件来进行数据处理,主要研究在服务水平约束下多级供应链网络优化问题。
2.2 模型介绍
本文事先做如下假定:
(1)客户的位置、需求是固定且已知的;(2)每个设施都能满足客户的全部需求;(3)每个客户的需求只能被一个设施全部满足;(4)存在设施备选集;(5)总仓没有固定运营成本。
约束条件:
(1)客户J需求一次性全部满足;(2)设施数量为P个;(3)每个地点的设施在W个规模下至多选1个;(4)提供服务的设施必须已经开放;(5)一定距离内满足客户需求不低于某个百分比。
目标函数为总成本最小,其中总成本包含四项:总仓到配送中心运输成本、配送中心到客户的运输成本、总仓到客户的跨级运输成本、配送中心运营成本。服务水平指的是一定条件下满足客户要求的供应链服务的数量占总客户订单数量的百分比,主要参数指标是满足客户流量(单位为件,下同)占总客户流量的百分比,模型中用百分比来表示。
目标函数:

符号说明:
W为备选配送中心集合;w为特定备选配送中心;I为配送中心集合;i为特定配送中心;H为总仓集合;h为特定总仓;d为客户j对产品的需求;X为是否建立配送中心;transSW为将产品从总仓h运送到配送中心i的运输成本;transWC为将产品从配送中心i运送客户j的运输成本;transSC为将产品从总仓h运送客户j的运输成本;whFixX为配送中心的固定成本;vol为配送中心i绑定给客户j单位产品消耗的空间量;whCap为配送中心的容量;Y为配送中心i是否运送货物到客户j;Z为从总仓h运送到配送中心i的产品数;V为总仓h是否运送产品到客户j。
其中:约束式(2)表示总仓与客户的对应关系;约束式(7)、式(8)、式(9)表示多级服务水平约束,约束式(12)、式(13)表示非负约束和0-1变量约束。
3 案例算法
3.1 案例背景
A公司是一家纸品流通企业,主营一种纸品,其销售网络遍布中国,在全国拥有57个配送中心,427家门店,拥有一个总的配送中心。随着业务的增长,企业拟在常熟建立总仓,采取总仓—配送中心—客户的三级供应链模式,此处设定总的配送中心的运营成本为0,每个配送中心的运营成本为200万元,配送中心到客户的单位运输成本为0.01元/(件*km),总仓到配送中心的单位运输成本为0.007元/(件*km)。
近几年,纸品企业的竞争越来越激烈,利润逐年下降,库存和压力成本逐步加大,基于企业的发展策略,现在需要设计并优化供应链网络以降低服务成本和提高服务水平。
模型所需要的信息选取该公司2020年度的订单信息作为订单基础数据,由于数据庞大,不在文章中一一列表,在软件运行之时会导入系统。
根据调研,本文确定送货卡车的平均行驶速度仅为60公里/小时。每天工作8小时,即一天行程为480公里。拟进行如下情景分析:
情景1:三级供应链的配送中心优化选址;
情景2:客户服务水平80%的三级优化选址;
情景3:客户服务水平85%的三级优化选址;
情景4:客户服务水平90%的三级优化选址;
情景5:允许跨级服务后的配送中心重新优化选址。
3.2 优化方案
(1)第一种情况:三级供应链的配送中心优化选址
把模型和数据输入软件系统,得出结果:选择8个配送中心,分别是辽宁、贵阳、乌鲁木齐、西安、长沙、苏州、常熟、济南。如图1所示,优化具体数据见表1。(以下所有图例中,·表示客户,★表示配送中心,—表示客户流量,→表示设施间流量)
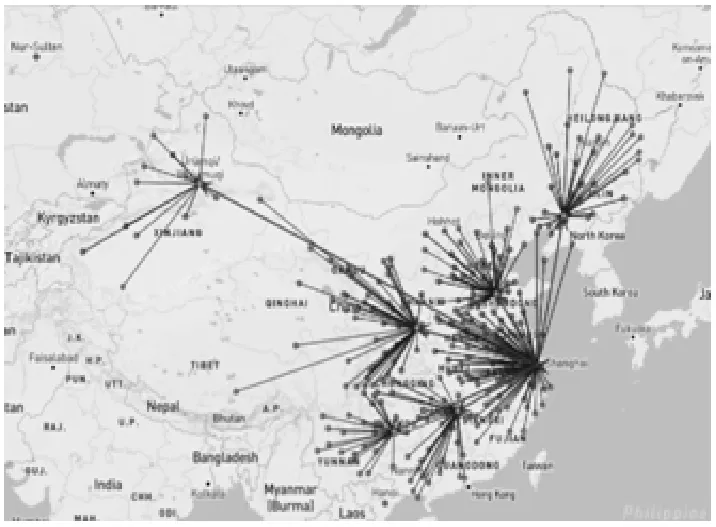
图1 三级供应链优化选址
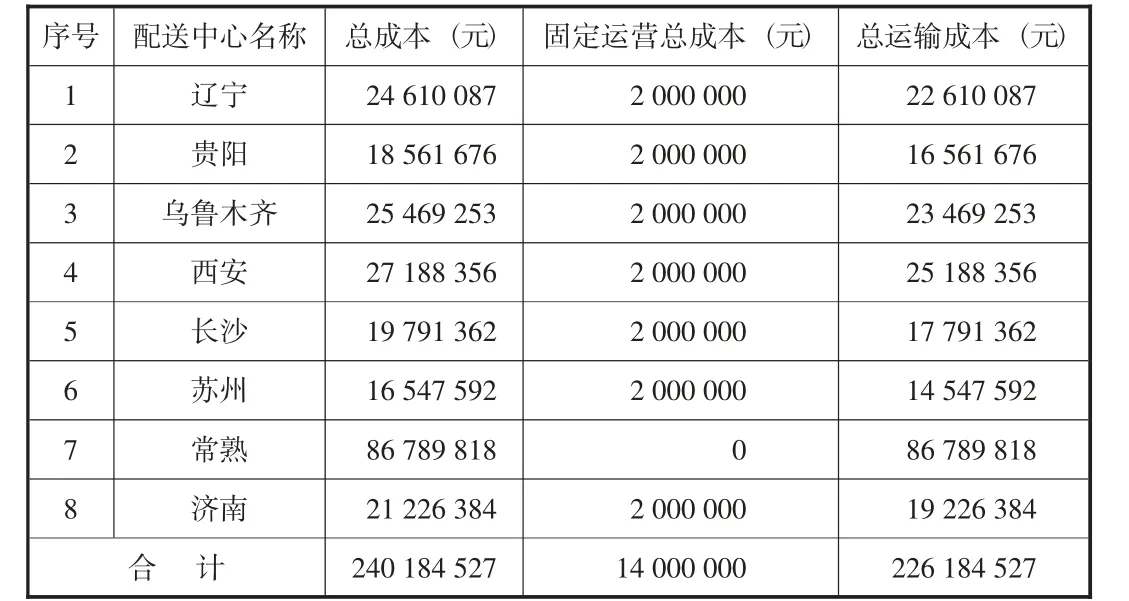
表1 三级优化选址情况一览表
最小总成本模型下,配送中心到客户一日达服务水平满足率54.7%,总仓到配送中心三日达服务满足率为83.6%。
(2)第二种情况:客户服务水平80%的三级优化选址
把模型和数据输入软件系统,得出:选择11个点:贵阳、太原、乌鲁木齐、西安、武汉、柳州、长春、无锡、常熟、大连、济南,具体情况见图2和表2。

图2 服务水平为80%的优化选址
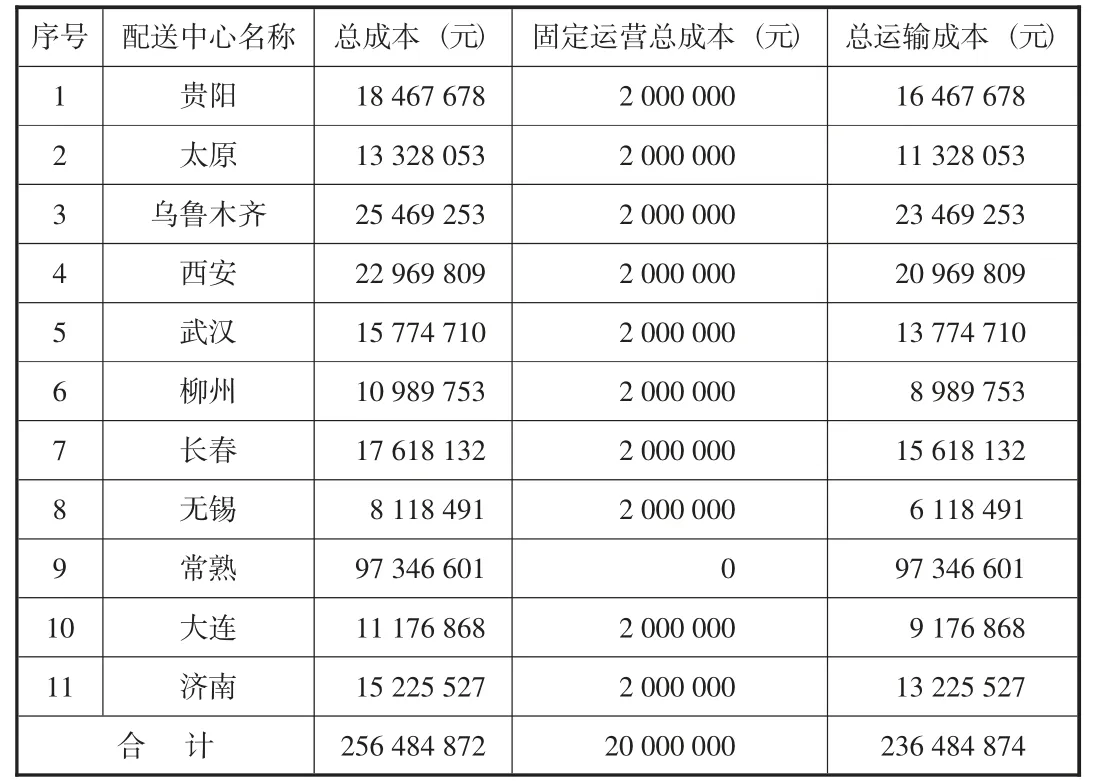
表2 客户服务水平80%的三级优化选址一览表
最小总成本模型下,配送中心到客户一日达服务水平满足率80%,总仓到配送中心三日达服务满足率为68.5%。
(3)第三种情况:客户服务水平85%的三级优化选址
把模型和数据输入软件系统,得出结果:选择开设12个点:贵阳、太原、乌鲁木齐、西安、兰州、武汉、柳州、长春、无锡、常熟、大连、济南,具体情况见图3和表3。

图3 服务水平为85%的优化选址

表3 服务水平为85%的三级优化选址一览表
最小总成本模型下,配送中心到客户一日达服务水平满足率85%,总仓到配送中心三日达服务满足率为62.8%。
(4)第四种情况:客户服务水平90%的三级优化选址
模型和数据输入软件系统,得出结果:
此时开设14个点:株洲、重庆、合肥、贵阳、太原、乌鲁木齐、锦州、西安、兰州、柳州、苏州、长春、常熟、济南,具体情况见图4和表4。
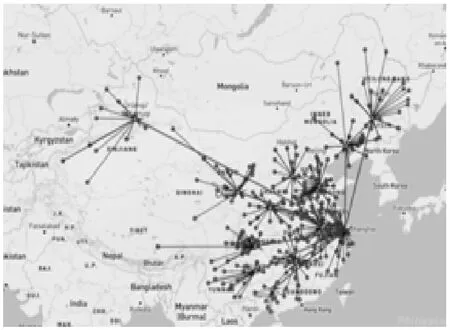
图4 服务水平为90%的优化选址

表4 服务水平为90%的三级优化选址一览表
最小总成本模型下,配送中心到客户一日达服务水平满足率90%,总仓到配送中心三日达服务满足率为61.5%。
(5)第五种情况:跨级服务的三级优化选址
所谓跨级采购,就是客户可以越过配送中心,可以直接从总仓订货(如图5所示)。模型和数据输入软件系统,得出结果:
此时开设7个点:辽宁、贵阳、乌鲁木齐、西安、长沙、常熟、济南,具体情况见图5和表5。

表5 跨级采购的三级优化选址一览表

图5 跨级采购的优化选址
最小总成本模型下,配送中心到客户一日达服务水平满足率54.7%,总仓到配送中心三日达服务满足率为55.4%。
4 总 结
以最小化总成本为目标,在以上5种不同的研究条件下,总成本和服务水平是不同的,所需要的配送中心的数量也是不同的,具体情况见表6。
分析:
三级供应链在以总成本为目标的选址条件下,配送中心位置及数量会产生变动。考虑服务水平时,优先满足客户端,则配送中心运营成本的增加(配送中心数量增多)、同时配送中心的选择更靠近客户端,一般伴随出站成本减少,入站成本增加,这样换取了客户端服务水平的提高;同时还伴随着总仓到配送中心服务水平的降低为代价。
如果可以考虑跨级服务,总成本具有进一步优化的空间。从实践来看,需要跨级采购的情况是采购量比较大的情况,这时跨级服务时采用整车运输,可替代运输成本较高的三级采购运输,这时,配送中心的数量会急剧减少,总成本也较大幅度地减少,最终的配送中心选址也会发生变化。
具体到本案例,企业可以根据自己的实际来选择最合适的潜在的配送中心作为自己的选址方案,如果只从成本出发考虑,可以允许跨级服务后重新选址方案,其他的情况按企业跟客户沟通或者合作情况来选择不同服务水平下的选址。

表6 5种情况下网络优化服务水平和总成本对比一览表
——HeightsTM用高效率和智能化提升服务水平

