基于分数阶广义积分器的电网同步技术

何宇 邓小龙 罗琦

0 引言

20世纪中后期以来,在能源短缺、环境污染和生态破坏等因素的主导和推动下,为适应能源发展战略,将多样性、复杂性和间歇性的可再生能源发电安全、有效地并入公共电网是一项极富活力又具有挑战性的课题[1-2]．作为以电力电子技术为基础的新一代功率变换设备,并网逆变器承担着将新型绿色能源发出的电能输送至电网的任务[3]．在逆变器的并网控制中,电网同步技术是整个并网发电系统的基石,已成为系统并网运行的关键技术之一[4]．

锁相环(Phase Locked Loop,PLL)是研究电网同步技术的基本工具,其提供的电网相位能够调整电网电压和并网电流之间的相位差,从而保障并网逆变器的可靠运行[5];PLL提取的电网频率、幅值在公共电网停止供电后可作为孤岛检测[6-7]的判断依据;PLL分离出的电网基波正、负序分量(Fundamental Positive- and Negative-Sequence Components,FPSC/FNSC)在电网电压发生跌落时，通过相应控制可用来实现逆变器的低电压穿越功能[8]．可见,PLL设计的优劣直接影响逆变器的并网质量．因此,基于并网逆变器的PLL技术值得深入研究．

在并网逆变器的发电系统中,基于同步旋转坐标系(Synchronous Rotating Frame,SRF)的PLL是基本的电网同步技术[9],在理想电网中具有十分突出的锁相能力,但在畸变不平衡的电网环境下无法准确捕获到电网FPSC的相位[10]．为能提取出纯净的FPSC,通常在SRF-PLL之前配置一个预滤器(Pre-Filter,Pre-F),如此构成的PLL称之为前置滤波器型锁相环[11]．常见的Pre-F-PLL有解耦双同步旋转坐标系型PLL[12-13]、自适应陷波器型PLL[14-15]、复数滤波器型PLL[16-18]和二阶广义积分器(Second-Order Generalized Integrator,SOGI)型PLL[19-24]等．文献[11-12]经论证指出,这些Pre-F-PLL关于相位的数学模型是一致的;文献[25]通过对比实验表明,这些Pre-F-PLL在控制性能上的表现基本无异．在Pre-F-PLL中,SOGI-PLL因其控制原理简单明了、控制算法易于实现和控制效果稳定可靠等优点被广泛采用,故本文以SOGI-PLL为载体对电网同步技术展开探讨．

目前对SOGI-PLL的研究主要致力于提高系统的控制性能．文献[19]在SOGI-PLL中引入了“慢频率适应器”,并用信号流图的方法论证了该算法可以加快系统的响应速度．文献[20]将两个SOGI模块串联在一起,构造出二重SOGI的正交信号发生器(实质上是一个四阶线性系统),认为基于此信号模块的PLL具备更强的抗干扰能力．文献[21]采用多个谐波消除模块级联的结构预先滤除电网中的各次谐波,提高了SOGI-PLL对谐波的抑制能力．然而,这些文献在对SOGI-PLL分析时,并未将前级SOGI模块和后级SRF-PLL结合起来研究,忽略了两者之间的影响,未能完整、全面地诠释出系统的控制性能．文献[22]在SOGI-PLL结构中加入了补偿环节,提出了固定频率的SOGI(Frequency-Fixed SOGI,FFSOGI)技术,即不再需要频率反馈环,从而可以提高系统的动态性能．但文献[23]指出,FFSOGI-PLL在非理想电网环境中无法精确提取出电网幅值．文献[24]利用共形映射法将SOGI拟合成一个分数阶系统,当电网频率发生波动时,改变引入的补偿参数,可使SOGI的阶数在2附近做自适应调整,解决了FFSOGI无法准确估计电网幅值的不足，但该算法中存在指数、对数、开方和反正切等运算,给数字控制器增加了大量运算负担．

为提高PLL系统的动态性能,本文提出一种基于分数阶广义积分器(Fractional-Order Generalized Integrator,FOGI)的PLL技术．所设计的前级FOGI模块的截止频率在相同性能指标下相比SOGI有了显著提高．为保证分析的全面性和准确性,将前级FOGI结构和后级SRF-PLL结合起来研究,同时保留了从后级到前级的频率反馈环．经三阶最佳设计法校正后,FOGI-PLL的动态指标明显优于SOGI-PLL．最后的仿真和实验结果表明,FOGI-PLL在数字实现时无需复杂的数学运算,且表现出比SOGI-PLL更好的动态行为．

1 三相SOGI-PLL的性能分析

这里以三相SOGI-PLL为载体进行分析与研究,该PLL的系统结构框图[12]如图1所示．

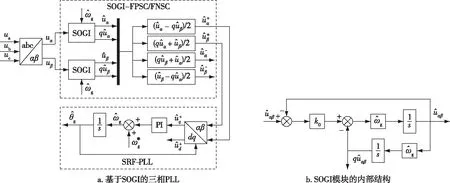
图1 三相SOGI-PLL的结构框图[12]Fig.1 Block diagram of three-phase SOGI-PLL[12]

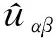
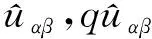
(1)

对照二阶线性系统的标准型,可得:

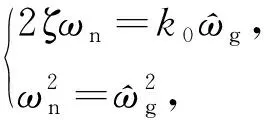
(2)

式中:ζ，ωn分别为系统的阻尼比和自然角频率．

将式(2)中的ωn消去,得:

k0=2ζ.

(3)

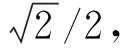
文献[25-26]通过推导得出整个PLL系统关于基波正序相位的等效开环传递函数G0(s)为

(4)

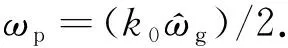
(5)

根据三阶最佳设计法[25-27],可得G0(s)的系统相角裕度γ为

(6)

式中:ωc为系统的开环截止角频率．

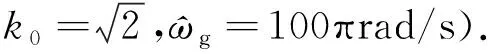
经典控制理论[27]指出:若期望某控制系统展现出一个优异的动态响应过程,要将其相角裕度设定在45°～70°．相角裕度超过70°,系统的稳定程度过好,动态收敛速度会变得十分缓慢;相角裕度低于45°,系统的稳定性会变差,且对参数的变化较为敏感．由图2可知,要使γ处于45°～70°,ωc的取值范围为39.17～92.02 rad/s．

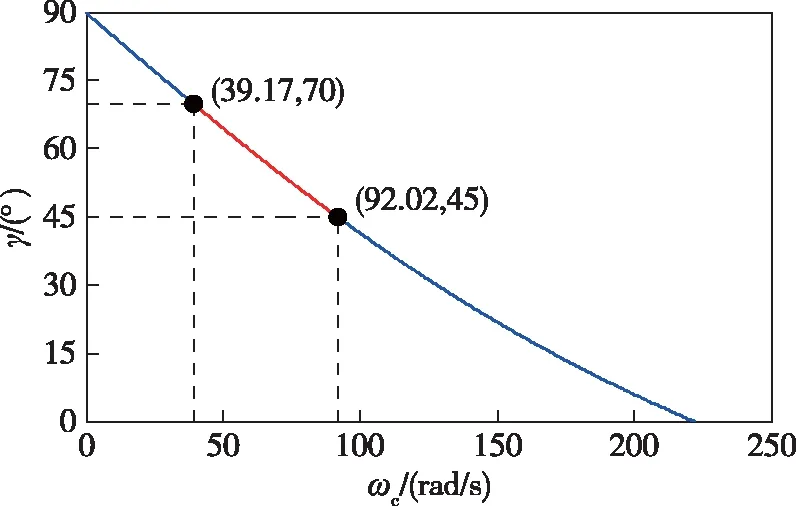
图2 ωc变化时G0(s)的相角裕度Fig.2 Phase margin of G0(s) with various ωc

为能具体分析SOGI-PLL的动态性能,利用Matlab/Simulink仿真得出了ωc分别为39.17、55、75和92.02 rad/s时SOGI-PLL在电网频率突变+5 Hz下捕获频率的动态响应曲线(如图3所示)．

图3 SOGI-PLL在不同ωc时的频率响应曲线Fig.3 Frequency response curves of SOGI-PLL with different ωc

根据图2和图3,表1列出了SOGI-PLL在不同ωc时的动态指标值．

表1中:ts为调节时间;σ为超调量．

由表1可以看到：开环截止频率越高,SOGI-PLL的调节时间越短,系统的响应速度加快;而系统的相角裕度在降低,其超调量会变大．由于PLL的响应速度和超调量对逆变器的电压、电流控制都存在一定影响[28-29],故在设计PLL时要朝着“速度快、超调低”的方向去优化．

表1 SOGI-PLL在不同ωc时的动态指标值

如表1所示,SOGI-PLL在系统相角裕度为45°～70°时的最小调节时间为61.2 ms,而相关文献[19,25-26]通过相应设计后同样在电网频率突变+5 Hz条件下的调节时间却能处于40～50 ms．事实上,这些文献都是以牺牲其他控制性能来换取快速的瞬态响应．如文献[19]将开环截止频率设置为30 Hz(即ωc=188.5 rad/s,相角裕度远低于45°),而实验得出的频率超调量高达60%,远高于经典控制理论对高阶系统超调量的建议范围18%～32%[27];文献[25-26]通过调节阻尼系数k0对参数ωp做了修改,拓宽了ωc的可选范围,使得PLL在较大的ωc下仍能取得一个合适的相角裕度,但k0的改变直接影响了前级系统的阻尼比——如文献[25]的ωp设置为332 rad/s，对应的阻尼比为1.06,高于经典控制理论对阻尼比的推荐范围0.4～0.8[27],降低了前级滤波结构的控制性能．综上所述,如何在不降低整个PLL系统的相角裕度且不影响前级性能的前提下具备一个快速的动态响应值得深入研究．

由式(3)、式(5)和式(6)可知,若要保障前级性能,标准型SOGI-PLL难以增大ωp,从而无法在满意的相角裕度下拥有较高的ωc．因此,有必要对前级的SOGI-FPSC/FNSC结构做出改进．

2 基于FOGI的三相PLL

为改善动态性能,本文提出基于分数阶广义积分器(Fractional-Order Generalized Integrator,FOGI)的三相PLL,其控制结构如图4所示．

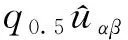
由图4可见,提出的FOGI-PLL分为前后两级:前级由FOGI模块和FPSC/FNSC模块组成;后级为SRF-PLL．前级的两个FOGI模块均可生成一对相位差为45°的斜交信号,这四个信号经FPSC/FNSC模块的线性运算后能够得到电网的FPSC和FNSC,其中FPSC的频率、相位等信息可被后级的SRF-PLL精确提取出来．

图4 三相FOGI-PLL的结构框图Fig.4 Block diagram of the proposed three-phase FOGI-PLL

SOGI使用两个一阶积分器来构造结构,而所提FOGI采用的是两个半阶的分数阶积分器．分数阶控制(Fractional-Order Control,FOC)是当前比较热门的前沿控制技术,作为整数阶控制的推广,能更全面、更准确地描述控制系统[30],已在工业机器人[31]、电力电子[32]、电力系统[33]和图像处理[34]等领域得到了成功应用．因此,将FOC融入到PLL中势必会获得一个更好的控制效果．

2.1 FOGI-FPSC/FNSC模块的特性分析

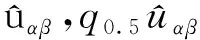
(7)

根据式(7),该模块对应的系统特征方程为

(8)

解得特征根为

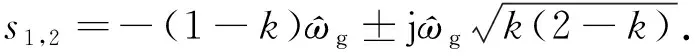
(9)

(10)

消去式(10)中的ωn,得:

k=1-ζ.

(11)

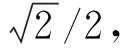
图5 D(s)和Q0.5(s)的Bode图Fig.5 Bode diagrams of D(s) and Q0.5(s)

假设电网电压uαβ的表达式(为不使后续推导复杂化,这里暂不考虑电网中存在谐波)为

(12)

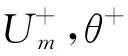
(13)

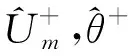
由以上对图5的分析可知:

(14)

由图4a中FPSC/FNSC模块的线性关系可得:

(15)

将式(13)代入式(15)并化简得:

(16)

综合式(12)、式(14)和式(16)可知,FOGI-FPSC/FNSC模块能准确分离出电网中的FPSC和FNSC．

2.2 FOGI-PLL关于基波正序相位的数学模型

2.2.1 前级关于基波正序相位的数学模型

由式(16)可求得:

(17)

将式(17)两端对时间t求导得:

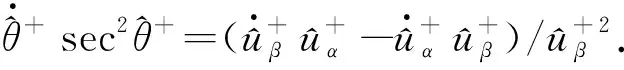
(18)

根据式(15),可将式(18)化为

(19)

由式(7)可得:

(20)

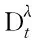
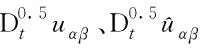
(21)

将式(12)、式(13)和式(21)代入式(20),再同式(16)一并代入式(19),并将结果整理得:

(22)

(23)

在式(23)中令:

(24)

则式(23)可转化为

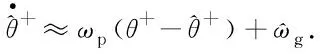
(25)

式(25)即为前级FOGI-FPSC/FNSC模块关于基波正序相位的时域数学模型,其复数域的结构框图如图6所示．

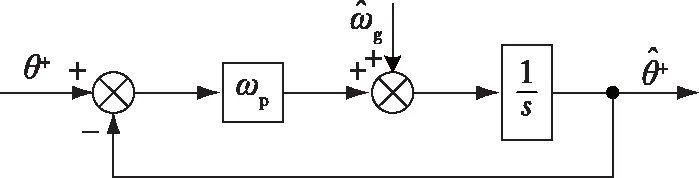
图6 前级的数学模型Fig.6 Mathematical model of the front-stage

2.2.2 后级关于基波正序相位的数学模型

后级是基本的SRF-PLL,在文献[9-12]都有详细介绍,这里不再赘述．SRF-PLL关于基波正序相位的数学模型如图7所示．

图7 后级的数学模型Fig.7 Mathematical model of the post-stage

2.2.3 整个PLL关于基波正序相位的数学模型

结合图6和图7,可得整个PLL系统关于基波正序相位的数学模型如图8所示．

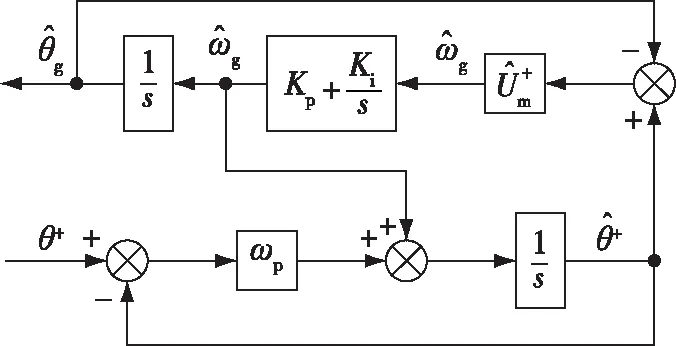
图8 FOGI-PLL的数学模型Fig.8 Mathematical model of FOGI-PLL

根据结构图的简化规则[27],可将图8等效变换为图9所示的单位负反馈控制系统．

图9 FOGI-PLL的等效数学模型Fig.9 Equivalent mathematical model of FOGI-PLL

由图9可得系统的开环传递函数G(s)为

(26)

由式(26)可知,该控制系统的型别为Ⅱ型,对电网相位这样的斜坡输入不存在稳态误差．

2.3 SOGI-PLL与FOGI-PLL的对比分析

根据式(3)和式(5)、式(11)和式(24),可得SOGI-PLL与FOGI-PLL的ωp分别为

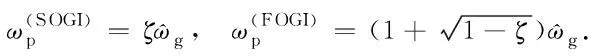
(27)

由于控制系统通常处于欠阻尼状态运行,即0<ζ<1,故在相同ζ下,有:

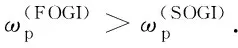
(28)

由式(4)和式(26)可知,SOGI-PLL与FOGI-PLL关于基波正序相位的小信号数学模型是一致的,因此它们属于同一类Pre-F-PLL,可在相同的研究基础上进行对比．由于研究的是三阶控制系统,为获取最大的相角裕度,这里采用三阶最佳设计法[25-27]对两者做对比分析．

在该设计方法下,开环截止角频率ωc为中频区的几何中心,且中频区宽度H和相角裕度γ为

(29)

根据式(29),图10给出了SOGI-PLL与FOGI-PLL取相同ωc和相同γ时的Bode示意图．

图10 SOGI-PLL与FOGI-PLL的Bode示意图Fig.10 Bode diagrams of SOGI-PLL and FOGI-PLL

图10中,ωz表示系统的开环零点．

由式(29)和图10可见：若SOGI-PLL和FOGI-PLL选用相同的ωc(使它们具备相近的响应速度),则FOGI-PLL的中频区宽度更长、相角裕度更大,而相角裕度的增大能促使系统的稳定性增强、超调量减小;若两者的相角裕度相同(使其超调量相近),则它们的中频区宽度相等,但FOGI-PLL拥有一个更高的ωc,而ωc的增大能加快动态响应．综上所述,合理提升ωp有助于改善PLL系统的动态调节能力．

为更具体对比SOGI-PLL和FOGI-PLL的相关数据,图11根据式(29)绘出了G(s)在ωc变化时的相角裕度曲线(取ωp=484.18 rad/s)．

图11 ωc变化时G(s)的相角裕度Fig.11 Phase margin of G(s) with various ωc

由图11可以看到,FOGI-PLL的ωc在系统相角裕度处于45°～70°时的可选范围为

85.38 rad/s≤ωc≤200.55 rad/s.

(30)

该范围明显超出SOGI-PLL中ωc的取值范围39.17～92.02 rad/s,因此,FOGI-PLL势必能解决SOGI-PLL在合适的相角裕度下响应速度偏低的问题．

2.4 FOGI-PLL的参数整定

三阶最佳设计法校正系统时,ωc需满足:

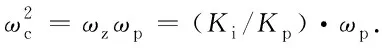
(31)

由式(26)可知,ωc的值由式(32)决定．

(32)

联立式(31)和式(32),可解得:

(33)

ωc的大小直接影响系统的响应速度,在高阶控制系统中,ωc与调节时间ts的关系[27]为

35°≤γ≤90°.

(34)

目前绝大多数PLL算法[16-17,19,25-26]的调节时间都能控制在50 ms以内,即ts≤50 ms,由式(29)和式(34)可求得(取ωp=484.18 rad/s):

155.84 rad/s≤ωc≤224.63 rad/s.

(35)

由式(30)和式(35)可进一步得到ωc的范围为

155.84 rad/s≤ωc≤200.55 rad/s.

(36)

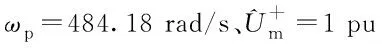
2.5 多重FOGI结构设计

为能彻底滤除电网中的各次谐波,本文仿照多重SOGI (Multiple SOGI,MSOGI)的构造[35],以提出的FOGI模块为基底,进一步设计了多重FOGI (Multiple FOGI,MFOGI)的结构,该控制结构的系统框图如图12所示．

图12 MFOGI结构Fig.12 MFOGI structure

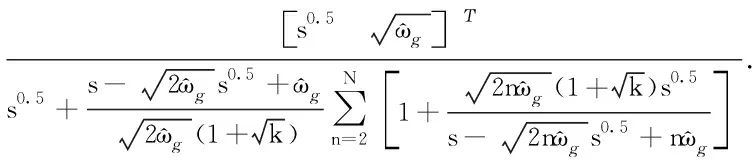
(37)

由式(37)可求得:

(38)

2.6 数字实现

分数阶微分/积分环节sλ(∀λ∈R)可采用基于滤波器设计的Oustaloup算法[30-32]在感兴趣的频段(ωb,ωh)作如式(39)所示的整数阶系统拟合．

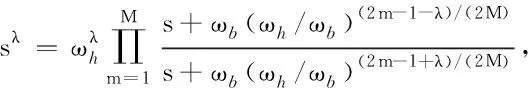
(39)

式中,M为Oustaloup滤波器的阶次．

为避免出现代数环和确保离散精度,采用三阶Adams-Bashforth算法[16,36]对文中出现的拉氏算子s进行离散化,具体实现方法如式(40)所示:

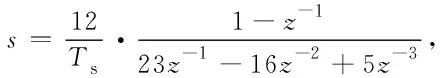
(40)

式中,Ts为采样周期．

3 仿真验证

为验证所提FOGI-PLL算法的正确性,采用Matlab/Simulink仿真对其进行测试．仿真时设置电网在0～0.1 s内为理想状态,即幅值为311 V、频率为50 Hz,且无负序、无谐波;0.1 s后,频率突变+5 Hz,且注入了20%的负序,并按国标[37]规定的最恶劣情况分别加入4%和3%的5次、7次谐波(使电网的THD达到5%)．仿真参数设为:k=0.293、Kp=170/311、Ki=10 147/311、M=3、ωb=2π·0.5 rad/s、ωh=2π·5 000 rad/s、Ts=50 μs．前级MFOGI结构中配置n=1、5和7．仿真结果如图13所示(图13e、f分别为FOGI-PLL与SOGI-PLL的对比仿真结果)．

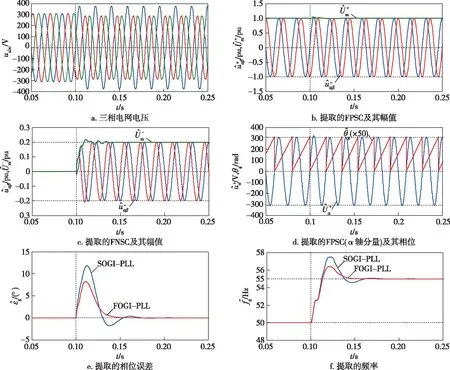
图13 仿真结果Fig.13 Simulation results

由图13a—c可知：电网变化后,分离出的FPSC除在电网电压突变的极短时间内略有波动外,其余时刻始终保持严格的正弦状态,其幅值稳定在1 pu不变;分离出的FNSC从零开始变化,并快速趋于稳定,稳定后同样呈现完美的正弦曲线,其幅值维持在预设的0.2 pu处不变．因此,FOGI-PLL能够成功分离出FPSC和FNSC．

由图13e、f的对比仿真结果可知,在近似的响应速度下,相比SOGI-PLL,FOGI-PLL在动态收敛过程中产生的超调更小,动态品质更好．具体的对比分析可见实验验证部分．

4 实验验证

为能更全面地展现FOGI-PLL在动态性能方面的优势,将该PLL与SOGI-PLL做了对比实验验证．控制芯片采用TMS320F28335 DSP,采样频率设定为20 kHz,DSP的内部变量(如电网的相位、频率和幅值等)由DAC7725数模转换芯片输出到Tektronix MDO3024示波器中观察．实验时设置电网的变化条件为“频率突变+5 Hz,并注入20%的负序、15%的5次谐波和10%的7次谐波”．FOGI-PLL的实验参数与仿真参数一致.SOGI-PLL的实验参数为:k0=1.414,ωc分别取78 rad/s(此时Kp=78、Ki=2 136)、125 rad/s(此时Kp=125、Ki=8 792)和170 rad/s(此时Kp=170、Ki=22 117),对应的γ分别为51.3°、31.3°和15.1°．两者前级分别采用MFOGI和MSOGI结构(均配置5次和7次滤波模块)．实验结果如图14所示．

图14 实验结果Fig.14 Experimental results

由图14a—c可见,电网变化后,FOGI-PLL在如此恶劣的电网环境中依然能够精确给出各信息:分离出的FPSC和FNSC在稳定时不含谐波,其幅值分别为1 pu和0.5/2.5=0.2 pu;提取到的相位误差在稳态时处于0°,捕获的相位无偏差地跟随基波正序变化;锁出的频率由50 Hz快速上升,最终无静差地稳定在55 Hz．因此,提出的PLL是一个稳定和无差的控制系统,可以实现准确的正负序分离、锁频和锁相,并能完全滤除电网中的主要谐波．

图14d—e展示了SOGI-PLL和FOGI-PLL在提取电网频率与相位误差上的对比结果．为能更具体对比两者在动态性能上的差异,表2根据实验数据列出了相应的动态指标值．结合表2、图14d和图14e可以看到:FOGI-PLL在ωc=170 rad/s(γ=51.3°)时的调节时间和超调量均符合前述设计要求;若SOGI-PLL的ωc与FOGI-PLL选为一致(170 rad/s),在电网突变后,SOGI-PLL虽能较快响应,但由于γ仅为15.1°,系统稳定性较差,其频率响应曲线和相位误差曲线均存在长时间振荡(尤其是频率响应曲线呈大幅度振荡,此时测量其调节时间已无实际意义),且频率超调量过大(达FOGI-PLL的2.7倍),虽降低ωc能在一定程度上缓解过高的超调,但无法在合适的超调下取得像FOGI-PLL这般的响应速度;若SOGI-PLL的γ与FOGI-PLL取为相同(51.3°),此时SOGI-PLL的稳定性较好,电网变化后的频率超调量与FOGI-PLL相近,但其调节时间和相位误差的超调均为FOGI-PLL的2倍以上,虽减小γ可以改善这两个指标,但无法在一个较快的响应速度下取得一个小的频率超调量．综上所述,FOGI-PLL能够兼顾响应速度和超调量,即可以实现小超调地快速响应,在控制性能上能表现出比SOGI-PLL更加满意的动态效果．

表2 SOGI-PLL和FOGI-PLL的动态指标

5 结论

为改善PLL的动态品质,在SOGI-PLL的基础上,提出了一种将二阶广义积分器改为分数阶广义积分器(FOGI)的PLL技术(FOGI-PLL)．通过理论分析、仿真验证和实验验证,可得出如下结论:

1) 制约SOGI-PLL动态性能的本质原因为前级SOGI结构的截止角频率ωp较低．该ωp值会导致SOGI-PLL无法在一个合适的相角裕度下获得很高的响应速度．

2) 所提FOGI结构的ωp在相同系统阻尼比下有了显著提高,这使FOGI-PLL取较大的开环截止频率时也能拥有比较满意的相角裕度．

3) 采用相同的方法(三阶最佳设计法)对SOGI-PLL和FOGI-PLL校正后,FOGI-PLL的动态指标明显优于SOGI-PLL．

4) 电网各参量发生突变时,FOGI-PLL能够稳定、快速和准确地完成电网正负序的分离、频率的提取和相位的捕获，展现出的动态行为比SOGI-PLL更优异．

5) 在恶劣的电网环境中,设计的多重FOGI(MFOGI)结构能有效抑制电网中的主要谐波．