两种轻型落锤式弯沉仪的参数标定与差异研究★

任 越,何博文，成林燕

(1.山西交通控股集团有限公司吕梁北高速公路分公司，山西 吕梁 033199；2.同济大学道路与交通工程教育部重点实验室,上海 201804)

轻型落锤式弯沉仪(LWD)是一种较新的路面结构无损原位测试仪器。LWD利用落锤从适当高度落下产生动力脉冲，在待测面表面产生相应的弯沉，测量的弯沉可用于反算确定测试结构层的层顶当量模量，评价结构层整体刚度。由于其冲击荷载较小，产生的弯沉也较小，常用于测试路基、粒料层等较为软弱的路面结构层。

国内段丹军等[1-12]将LWD应用于路基，通过对比LWD检测模量Ep和一系列的室内实验结果(如室内承载板试验、室内足尺寸路面灌砂法实验等)、室外现场试验结果(如室外承载板试验、贝克曼梁试验等)，建立了LWD检测模量Ep和压实度K的良好回归关系；将LWD所测弯沉和贝克曼梁弯沉良好地关联起来。国外也有较多研究和规范基于LWD的对粒料层和路基的压实质量控制方法，如美国ASTM标准[13-14]、美国明尼苏达交通部研究报告[15-16]、欧盟的LWD实施规范(CEN ICS 93.020)、美国印第安纳州交通部研究报告等。然而，关于LWD荷载的时间分布的研究较少，Sebaaly等[17]通过分析FWD数据，指出荷载时程曲线与弯沉时程曲线以及其余各弯沉传感器之间存在相位滞后的现象。由于相位滞后的存在，两种瞬时弯沉盆(荷载达到峰值时刻的弯沉盆和1号弯沉传感器达到峰值时刻的弯沉盆)与峰值响应产生的弯沉盆有很大不同，对层模量的大小有显著影响。这表明了时间分布是冲击荷载重要动态效应因素，与FWD相似的LWD的研究中需要加以考虑。另外，Sadaf发现不同种类LWD也会有差异，通过在梁验证测试仪(BVT)进行上述三种LWD测试和四点钢梁测试的对比试验，对三者的性能差异进行研究。结果表明，LWD 测试所得的钢梁峰值刚度kp-LWD(LWD荷载峰值Fpeak与测得弯沉dpeak之比)与四点钢梁测试的模拟静荷载刚度ks高度接近，由此认为仅采用LWD荷载峰值即可以较好地估计钢梁的刚度[18]。

综上所述，现有的国外研究缺乏对LWD进行动态效应的标定，包括动荷载时间和空间分布两方面的特征。同时，不同类型的LWD的参数也有显著的区别，包括荷载板类型、有无荷载传感器等，需要对其差异深入研究。为此本文对两种不同LWD(单点式和多点式)冲击荷载的动态效应进行了探究，通过建造试验坑进行足尺寸实验，标定了两种LWD荷载的时间分布，并分析了两者的差异，以期为今后LWD在粒料层施工质量控制的进一步应用奠定基础。

1 两种LWD检测设备的参数对比

实验所使用的仪器包含单点式轻型落锤式弯沉仪和多点式轻型落锤式弯沉仪各一台，分别为北京高铁建科技发展有限公司所产的GTJ-Evd型动态变形模量测试仪和德国TERRATEST公司所产的TERRATEST 9000 LWD。相关参数如图1所示。GTJ-Evd型LWD落锤高度固定为70 cm，下方缓冲装置为不可拆卸的长条状橡胶圈，落锤质量固定为10 kg，荷载板尺寸固定为直径d=300 mm，无附加弯沉传感器。TERRATEST 9000 LWD相较于GTJ-Evd型LWD，落高、锤重、荷载板尺寸、橡胶垫个数均可选。落高最大为90 cm，落锤可选质量为10 kg，15 kg，20 kg，荷载板直径可选100 mm，150 mm，200 mm，300 mm，缓冲橡胶垫可选个数为3个或4个，相互为并联关系，另有两个附加弯沉传感器。

为便于描述，根据有无附加传感器的特点将GTJ-Evd型LWD和TERRATEST 9000 LWD分别称为“单点式LWD”和“多点式LWD”。

2 实验方法

2.1 足尺寸现场标定实验用材

标定试验用材包括三种粒料材料和土压力盒。

粒料采用优质机制石灰岩碎石作为原材料，其材料性能、规格均符合规范要求[19-20]，经考虑设计了如表1所示的三种级配。

表1 粒料层各级配组成范围

A,B两种均为设计级配的级配碎石，C为混合石屑。考虑到级配碎石的最大粒径越大，其试验结果变异性越大，故设计A,B两种级配的最大粒径为13.2 mm。由室内标准重型击实试验[21]求得A，B两种级配的最大干密度分别为2.25 g/cm3和2.39 g/cm3，最佳含水率(质量分数)分别为5.10%和5.90%。

土压力盒及传感器设备可埋设于待堆填的粒料材料中，用于监测两种LWD在各阶段层顶测试过程中土压力的变化全过程，包含冲击应力的峰值、作用时间、应力时程曲线形状等关键信息。采用长沙翔昊电子科技有限公司所产的XHZ-4XX系列电阻式双膜土压力盒。工作面受力变形特征是平面位移，对不同性质的介质，有良好的适应性，适用于碎石材料，其量程为0.2 MPa，精度为0.2 kPa，尺寸为φ34 mm×25 mm。

考虑到LWD施加的冲击荷载作用时间极短(一般为20 ms以内)，配套传感器须提供较高的采集频率，所以采用东华测试所产的DH5922D动态信号测试分析系统，其最大可提供100 kHz的采集频率，实际监测LWD测试的过程中采用5 kHz即可满足要求，即每隔0.2 ms采集一点。

2.2 足尺寸试验坑的建造及粒料堆填施工

对于LWD荷载的时间和空间分布，采用足尺寸实验进行探究。在室内建造两长宽高分别为1 m,1 m,1.3 m的试验基坑(尺寸参考文献[22])，按图2所示进行逐层粒料堆填压实并在各层层顶中心点进行LWD测试。在图2所示位置各布设3个土压力盒编号为e1,e2,e3，其中e3用于测量竖向应力，位于LWD测点正下方2.5 cm处；e1,e2用于测量侧向应力，与e3的距离分别为10 cm,20 cm，3个土压力盒的位置应尽量保证共线。每次在土压力盒埋设前，在待埋设位置的土压力盒受力面垫少许细砂。每次堆填压实后在该层上进行LWD的测试试验，记录LWD测试过程中产生的附加压力。测试结束后，继续分别在两个坑的砂砾层上堆填A，B两种级配的粒料，并重复压实，LWD测试的试验步骤至五层压实测试完毕。

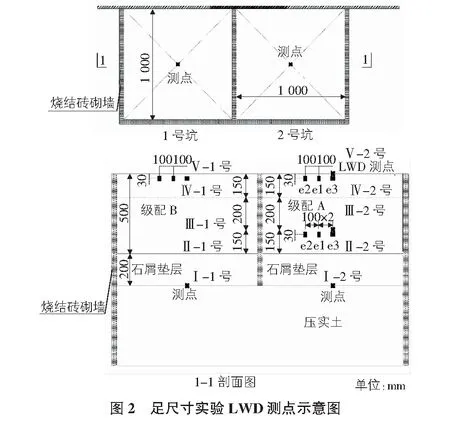
2.3 足尺寸现场标定实验方法

LWD所施加的荷载在时间分布上表现为极短时间内的冲击荷载。冲量可换算为作用力与时间的乘积：

(1)

其中，m为落锤的质量，kg;υ1为落锤接触橡胶垫时刻的冲击速度,m/s;P(t)为产生的作用力,kN;t为冲击荷载的作用时间,s。

常用的冲量引起的作用力P(t)的时间分布可近似处理为矩形、三角形、半正弦或半正弦平方分布,现引入“时间形状参数λP(α)T”对LWD作用荷载的本身形状进行描述,定义为:

(2)

其中，I为荷载作用的冲量，可通过P(t)函数对时间t积分得到，N·s;Td为冲击荷载的作用时间，ms;α为荷载折减参数,无量纲;Pα为α位荷载值，kN,其定义如图3所示,图3中Pm为荷载峰值，kN。对于任意荷载的时间分布,若存在唯一的荷载峰值Pm,t0取该值出现的时间点;若不存在唯一的荷载峰值(如矩形荷载),t0取Td/2。取t0±0.5αTd两时刻对应的荷载值Pα1和Pα2的平均值为Pα。

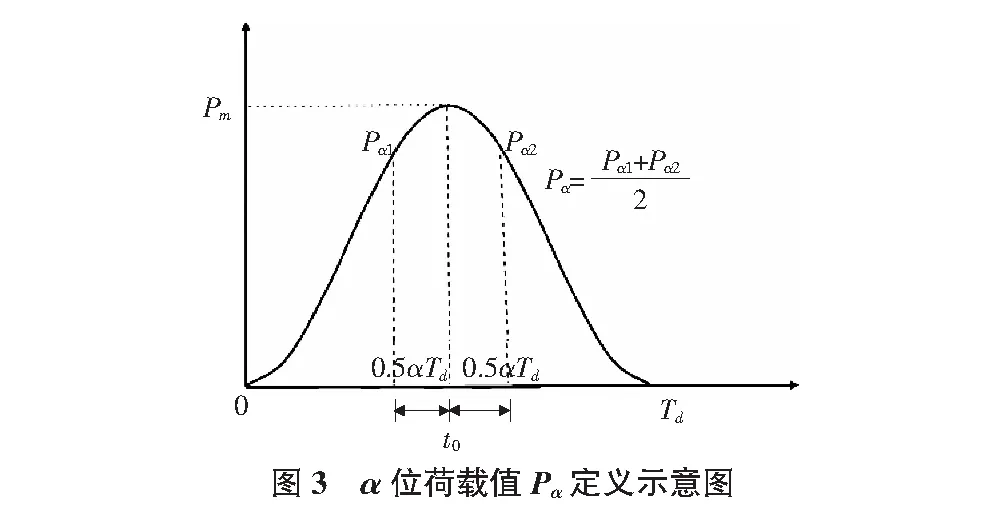
对于上述的几种对称荷载,有Pα1=Pα2。表2列出了α=0.05，0.1，0.15三种情况下上述几种荷载的时间形状参数λP(α)T。

表2 几种冲击荷载的时间形状参数λP(α)T

单点式LWD的测试荷载全过程未知，缺乏荷载峰值、荷载形状等关键信息。因此，为对单点式LWD关键参数如荷载的作用时间Td、时间形状参数λP(α)T进行标定，同时为对两种LWD冲击荷载的作用过程进行详细的比较研究，于1号坑级配B层顶中心点处进行了对照实验。

使用单点式LWD预压后在该点进行连续10次的单点式LWD独立试验，而后在相同位置更换为多点式LWD进行同样的10次独立试验，其落锤固定高度为85.7 cm，荷载板半径为15 cm，橡胶垫数量为4，落锤质量选用10 kg，未连接附加传感器。上述试验过程用传感器以5 kHz的频率进行全过程监测。

3 时间参数的标定

在两种LWD的10组弯沉数据中去除有明显误差的结果后，均各取与各自组内均值最为接近的6组结果进行分析。将选取的多点式LWD的6次竖向应力e3时程曲线应力产生起点平移至同一点，绘制图像如图4(a)中的线“1～6”所示，可以看出曲线有比较明显的震荡，这反映了LWD冲击荷载作用过程中仪器本身的自振；多点式LWD内置传感器所测得的荷载板上平均应力集度的时程曲线也绘制于图4(a)中，如21图4中的点“p1～p6”所示。图4(b)所示的是多点式LWD内置传感器所测得的荷载板上平均应力集度的时程曲线与半正弦、半正弦平方、三角形三种拟合荷载的对比图。

注意到图4(a)中竖向压力从产生到到达峰值所用时间与LWD仪器所得的荷载时程达到峰值的时间基本一致，而峰值大小有明显的差距，这可能反映了空间形状参数mq<1。将“1～6”等比放大至与“p1～p6”的峰值均值相同，二者各选取代表性的一组数据(如“2”和“p2”)求得决定系数R2=0.97，由此可以看出图4(a)，图4(b)的荷载形状较为相似，即土压力盒e3所测荷载形状对于实际路面荷载的还原度较高。下面就二者的时间参数Td和λP(α)T进行进一步的标定。

对图4给出的时程曲线图求面积，可以分别求得土压力盒实测与LWD仪器读得的冲量I，再将作用时间、峰值代入式(2)即可求得时间形状参数λP(α)T，列于表3中。此处表3中的平均值为除去最大值和最小值后的均值。

表3 多点式LWD的荷载冲量及时间形状参数λP(α)T

由表3可知，土压力盒所测得的荷载作用时间T与仪器所得荷载作用时间Td较为接近，误差约为1.3%，可认为仪器所测Td即可反映真实的路表荷载作用时间。α=0.05，0.1，0.15三种情况下，通过土压力盒所计算得的时间形状参数λP(α)T0与通过LWD仪器读数所计算得的时间形状参数λP(α)T1的误差均约为4.0%，这一结果也辅助证明了土压力盒所测压力时程曲线对于荷载时程曲线有较高的还原度。

图4(b)中三角形拟合荷载、半正弦拟合荷载、半正弦平方拟合荷载与LWD的实测荷载“p2”的决定系数R2分别为0.91，0.70，0.92，半正弦平方拟合荷载的R2最大，可见实际应用中可以采用半正弦平方荷载对多点式LWD荷载进行简化。

同样，用土压力盒所测结果对单点式LWD进行标定。单点式LWD的土压力盒所测6次竖向应力时程如图5中1～6所示，可以看出荷载形状较为稳定。出于简便应用的考虑，现对其进行分段拟合简化，采取的形式为“直线+直线+抛物线”的类梯形荷载，对于拟合形式确定的压力时程曲线，同样可以积分求得时间形状参数λP(0.05)T为1.160，最终拟合的压力时程曲线绘制于图5，如图5中“拟合”一线所示。

考虑到荷载曲线震荡带来的峰值不确定性，为提高拟合的精度，图5拟合压力时程曲线的峰值取Pm=52 kN，为第2次测试的压力峰值58.224 kN的0.89倍，作用时间取Td=14.1 ms。拟合后其与第2次曲线的决定系数R2达到了0.92，可见该拟合曲线准确度较高。

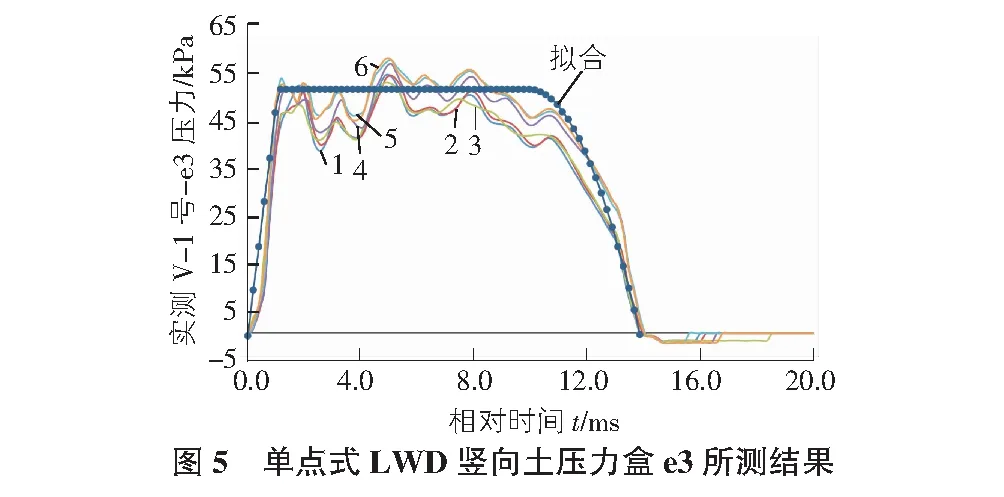
单点式LWD的6次土压力盒实测结果全部可用于求解时间形状参数λP(0.05)T。由于实测的压力时程曲线在分段2有一定的波动性，故采用上述图5的做法在计算λP(0.05)T前将实测峰值乘以0.89得到修正后的荷载峰值。作用时间T和冲量均由实测压力时程曲线图中求得，计算得到λP(0.05)T列于表4形状参数λP(0.05)T的均值为1.162，与表4中拟合压力时程曲线的形状参数1.160基本一致，该结果辅助验证了上述拟合的准确性。

表4 压力实测盒单点式LWD时程曲线的冲量及形状参数λP(0.05)T

据此，可由多点式LWD的仪器各层测试所读冲量近似换算出单点式LWD的各层冲量I；同时近似地认为各层上两种仪器的荷载作用时间Td之比为定值，由此换算出各层上单点式LWD的荷载作用时间。再根据标定的时间形状参数λP(α)T，代入式(2)可求出单点式LWD测试的各层荷载峰值Pm，结合图5中的拟合可以将单点式LWD的荷载时间分布P(t)完全确定。确定的荷载时间分布参数见表5。

表5 两种LWD各层荷载参数

由表5可知，单点式LWD的荷载峰值Pm明显小于厂家标定的7.07 kN，而粒料层上的作用时间Td也明显小于厂家所标定的(18±1) ms，且对于不同的路面结构该两参数不为固定值。

4 空间参数的标定

对于LWD荷载的空间分布，采用足尺寸实验探究了两种类型LWD的空间分布：

1)多点式TERRATEST 9000 LWD,板底为环空式(弯沉传感器从板底开孔中伸出),有两附加弯沉传感器,可记录完整的荷载时程曲线和荷载中心点处及两附加弯沉传感器处的弯沉时程曲线。

2)单点式GTJ-Evd型LWD,板底为一体式(荷载板与弯沉传感器一体),仅可测得荷载中心点处的弯沉峰值。

荷载中心点位置记为g0,多点式LWD的两附加弯沉传感器位置分两组:AC组,两传感器A点和C点距离g0分别为25 cm,40 cm;BD组,两传感器B点和D点距离g0分别为30 cm,45 cm。g0点及A～D四点共线。现利用多点式LWD的两附加弯沉传感器峰值,在模量反算过程中确定其荷载分布的空间形状参数mq,反算流程图见图6。

表6给出了多点式LWD于1号坑土基层上AC组的反算结果,LWD实测上述g0,A，C三个位置的弯沉峰值分别为Wg0,WgA和WgC,反算得到的理论弯沉峰值分别为W0，WA和WC。从峰值及其出现位置可以看出反算的精度较高。在该组反算结果中得到,多点式LWD于土基上的空间形状参数mq=0.35。

表6 1号坑土基层上多点式LWD的AC组反算结果

按照上述方法可以得到各堆填层的空间形状参数mq,汇总如表7所示。由表7可知,多点式的空间形状参数mq对于粒料层和粉质土分别为0.60和0.35,单点式的空间形状参数mq对于粒料层和粉质土分别为0.75和0.60。多点式的mq值小于单点式,这可能是两种仪器的荷载板类型不同造成的。

表7 各堆填层上的空间形状参数

相较于单点式的一体式荷载板,多点式的中心开孔式荷载板于板心处的直径约3 cm的开孔使得其在板心附近所施加的荷载小于单点式,故表现为更小的mq值。

5 结语

本文对LWD动态荷载的特征分空间分布和时间分布两方面进行了阐述，引入了“荷载时间分布形状参数λP(α)T”的概念对LWD冲击荷载的时间分布形状加以描述，空间分布方面采用“空间形状参数mq”描述圆形荷载的空间形状，并利用土压力盒时程曲线对两种LWD进行标定。结合冲击荷载作用的冲量和引入的“回弹高度比λh”，采用足尺寸现场实验对单点式和多点式两种LWD的荷载时间和空间分布形式进行标定，主要得到结论如下：

1)标定了单点式LWD和多点式LWD两种不同类型仪器的荷载参数，包括空间分布形状参数mq、时间分布形状参数λP(0.05)T、荷载形状。

2)厂商提供的单点式的荷载峰值Pm和作用时间Td参数明显偏大，不建议购置使用。如需使用，需要借助土压力盒重新标定单点式LWD时间分布参数。