深埋储层孔隙度迭代反演方法

田 军 刘永雷 徐 博 白建朴 李青霖

(东方地球物理公司研究院库尔勒分院，新疆库尔勒 841000)

0 引言

孔隙度是指示储层物性的关键参数之一，可用于精细油藏研究。岩石物理反演是定量预测孔隙度的主要手段，其思路是以岩石物理模型为基础，利用纵、横波速度等弹性参数反演孔隙度、泥质含量等物性参数[1-5]。现今的岩石物理反演方法主要以非线性岩石物理模型为基础，构建反演目标函数，并采用非线性算法求解，如蒙特卡洛法、模拟退火法等。但此类算法多解性强，且计算量巨大[6-8]。为此，近年来人们研究了线性反演方法。Grana[9]提出了对岩石物理模型线性近似的方法，并以此为基础，实现了三参数(储层孔隙度、泥质含量与饱和度)线性化反演，大幅降低了计算量与反演多解性，为在实际生产中推广应用奠定了基础。凌东明等[10]针对远离均值点模型近似结果偏差较大的问题，采用岩性约束相分段近似Xu-White模型，提高了储层物性预测精度。张佳佳等[11]以前人研究成果为基础，利用阻尼最小二乘算法直接求解线性化岩石物理反演问题，提高了三参数反演的计算效率。

现有的岩石物理线性化反演方法均为三参数反演，是将叠前弹性反演得到的纵、横波速度及密度作为已知量，求取孔隙度、泥质含量与饱和度三个未知量[9-11]。与纵、横波速度相比，密度对反射系数贡献较小，反演密度需要更大的叠前地震道集角度范围[12-13]。在储层深埋条件下，由于叠前地震道集反射角较小，导致密度反演结果不可靠； 在忽略密度项的情况下，岩石物理三参数反演方程为欠定形式，无法得到唯一解，从而限制了现有岩石物理线性化反演方法对深埋储层的预测。

在前人研究基础之上，本文提出一种基于迭代算法的储层孔隙度反演方法。该方法是在岩石物理模型线性近似的基础上，推导纵、横波速度与孔隙度、泥质含量的线性关系式，然后基于贝叶斯理论构建孔隙度迭代反演目标函数，再利用二分法迭代求解。该方法不依赖于密度项，适用于储层深埋条件的孔隙度反演。

1 孔隙度迭代反演方法

1.1 线性反演的局限性分析

岩石物理模型是岩石物理反演的基础，建立了储层物性参数与弹性参数之间的关系，可表示为

d=f(m)+e

(1)

其中

(2)

式中：d为由岩石纵波速度VP、横波速度VS和密度ρ组成的向量；f(m)为岩石物理模型函数，m为由孔隙度φ、泥质含量φ和含水饱和度SW组成的向量；e为误差向量。岩石物理反演以式(1)为基础求解模型参数m。在一般情况下，f(m)为非线性函数，需采用复杂的迭代算法求解，而此类算法多解性强，且计算量巨大，难以用于生产。为此，采用泰勒级数展开f(m)，保留一阶项得到线性近似式

d≅f(m0)+Jm0·(m-m0)+δ

(3)

其中

(4)

式中：Jm0为f(m)在已知点m0处的雅可比矩阵，在反演过程中可将m0设置为常值模型；δ为e的一阶近似。在实际应用中需根据目的层特征选择合适的岩石物理模型建模，得到适合的模型参数，进而计算f(m0)与Jm0。

令b=f(m0)-Jm0·m0，对式(3)重新整理，得到储层物性参数与弹性参数之间的线性关系式

(5)

式中：b(P)、b(S)和b(ρ)分别为泰勒级数展开后纵、横波速度和密度对应的系数项；δP、δS、δρ分别为泰勒级数展开后纵、横波速度和密度对应的误差项。现有的岩石物理线性反演方法均以式(5)为基础，构建目标函数求解[9-11]。式(5)为正定方程组，将叠前弹性反演得到的纵、横波速度及密度作为已知量，可以得到唯一的孔隙度、泥质含量与含水饱和度参数。但在储层深埋条件下，叠前道集反射角较小，无法达到反演密度需要的最小角度范围。若忽略密度项，则式(5)改为

(6)

式(6)包含两个方程、三个未知量，为欠定方程组，以此为基础进行岩石物理反演无法得到唯一解。因此，在储层深埋条件下无法得到可靠密度反演结果，导致常规岩石物理线性反演方法不适用。

1.2 孔隙度反演方程推导

式(6)为储层深埋条件下的纵、横波速度与孔隙度、泥质含量及饱和度的线性关系，雅可比矩阵系数项反映了不同物性参数对速度的贡献程度。在油、水两相饱和岩石中，孔隙度变化对速度影响最大，泥质含量次之，饱和度最小[14]，即纵、横波速度对饱和度变化不敏感。为此，将饱和度作为扰动项，则式(6)变为

(7)

由此可见，当给定初始饱和度时，式(7)为正定方程组，利用纵、横波速度即可反演唯一的孔隙度与泥质含量。因此，可以式(7)为基础，基于贝叶斯理论构建反演目标函数。

为公式推导方便起见，令

则式(7)简化为

d′=G·m′+δ

(8)

依据贝叶斯理论，后验概率密度分布函数正比于似然函数与先验分布的乘积[15]。假设误差项δ与先验模型参数m′均服从高斯分布，基于式(8)可构建后验概率密度分布函数近似式

P(m′|d′)≅λ×

(9)

(10)

的最小值。为此，令∂L/∂m′=0，得到反演方程

(11)

1.3 饱和度敏感性分析

利用式(11)求解孔隙度与泥质含量时，需给定饱和度项，即反演精度与饱和度准确程度相关。为验证反演结果对饱和度的敏感性，应用理论模型进行分析。

已知油、水两相流体饱和岩石孔隙度、泥质含量与含水饱和度曲线(图1a)，通过岩石物理正演得到纵波速度与横波速度(图1b)。在正演过程中，选用适用砂、泥岩储层的Xu-White模型[16]作为岩石物理模型。为进行极限测试，给定不同常值饱和度模型，利用纵、横波速度反演孔隙度与泥质含量，进而分析饱和度对反演精度的影响。

图2为不同饱和度模型的反演与正演结果。由图可见：当含水饱和度为1.00时，反演、正演结果均与模型曲线存在较大偏差(图2a)； 当含水饱和度为0时(与饱和度均值较接近)，反演、正演效果得到明显改善(图2b)； 当含水饱和度为0.50时(进一步逼近饱和度均值)，反演、正演效果进一步提升(图2c)； 当含水饱和度为模型均值(0.29)时，反演、正演结果与模型具有较好的一致性(图2d)。

图3为图2对应的反演结果绝对误差。由图可见，设定饱和度越接近模型饱和度均值，绝对误差越小，具体表现为：当饱和度为1.00时，孔隙度平均绝对误差为0.034，泥质含量平均绝对误差为0.106(图3a)； 当饱和度为0时，孔隙度平均绝对误差为0.013，泥质含量平均绝对误差为0.042(图3b)； 当饱和度为0.50时，孔隙度平均绝对误差为0.01，泥质含量平均绝对误差为0.033(图3c)； 当饱和度为模型饱和度均值(0.29)时，孔隙度平均绝对误差为0.003，泥质含量平均绝对误差为0.011(图3d)。因此，对于油、水两相的流体饱和岩石模型，反演结果对饱和度模型的精度要求低，给定合理的常值饱和度模型，即可保证相对反演结果的可靠性，说明反演结果对饱和度不敏感。

图1 油、水两相流体饱和岩石一维正演模型(a)储层物性测井曲线； (b)正演曲线各组分岩石物理参数为理论值[17]，根据实际工区特点取砂、泥岩组分孔隙横纵比分别为0.150、0.005

图2 不同饱和度模型的反演与正演结果(a)饱和度为1.00； (b)饱和度为0； (c)饱和度为0.50； (d)饱和度为模型均值(0.29)蓝色为模型曲线，红色为反演结果，绿色为利用反演的孔隙度、泥质含量与给定饱和度通过正演得到的纵、横波速度曲线

图3 图2对应的反演结果绝对误差(a)饱和度为1.00； (b)饱和度为0； (c)饱和度为0.50； (d)饱和度为模型饱和度均值(0.29)黑色实线为误差曲线，红色虚线为0值线

1.4 孔隙度迭代反演流程

由上述分析可知，反演精度取决于对真实饱和度均值的搜索，常值模型的饱和度越接近真实饱和度均值，反演精度越高。为此，本文采用二分法迭代求解式(11)，思路如下：

(1)分别设置初始模型的含水饱和度为0、1.00进行第一次反演，得到孔隙度与泥质含量，并基于岩石物理模型，结合反演结果正演纵、横波速度，并计算正演结果与实测结果的平均相关系数γ0、γ1；

(2)按二分法，对初始饱和度模型求平均，得到第二次反演所需的饱和度常值模型，即为0.50，并计算正演相关系数γ2，对比γ0，γ1，γ2，保留两项最大相关系数及对应饱和度进入下一轮反演；

图4 孔隙度迭代反演流程

(3)如果反演结果的精度满足要求，则终止迭代，输出最终反演结果，否则，求取平均孔隙度继续迭代，直到反演结果满足要求或达到最大迭代次数为止。

上述迭代反演方法可忽略密度项影响，仅利用纵、横波速度即可得到相对可靠的孔隙度(图4)。

2 模型试算

为验证孔隙度迭代反演方法的可行性与反演结果的有效性，利用一维正演模型(图1)进行测试。以正演过程采用的岩石物理模型为基础，利用纵、横波速度迭代反演孔隙度与泥质含量。

图5为一维模型孔隙度迭代反演结果，图6为

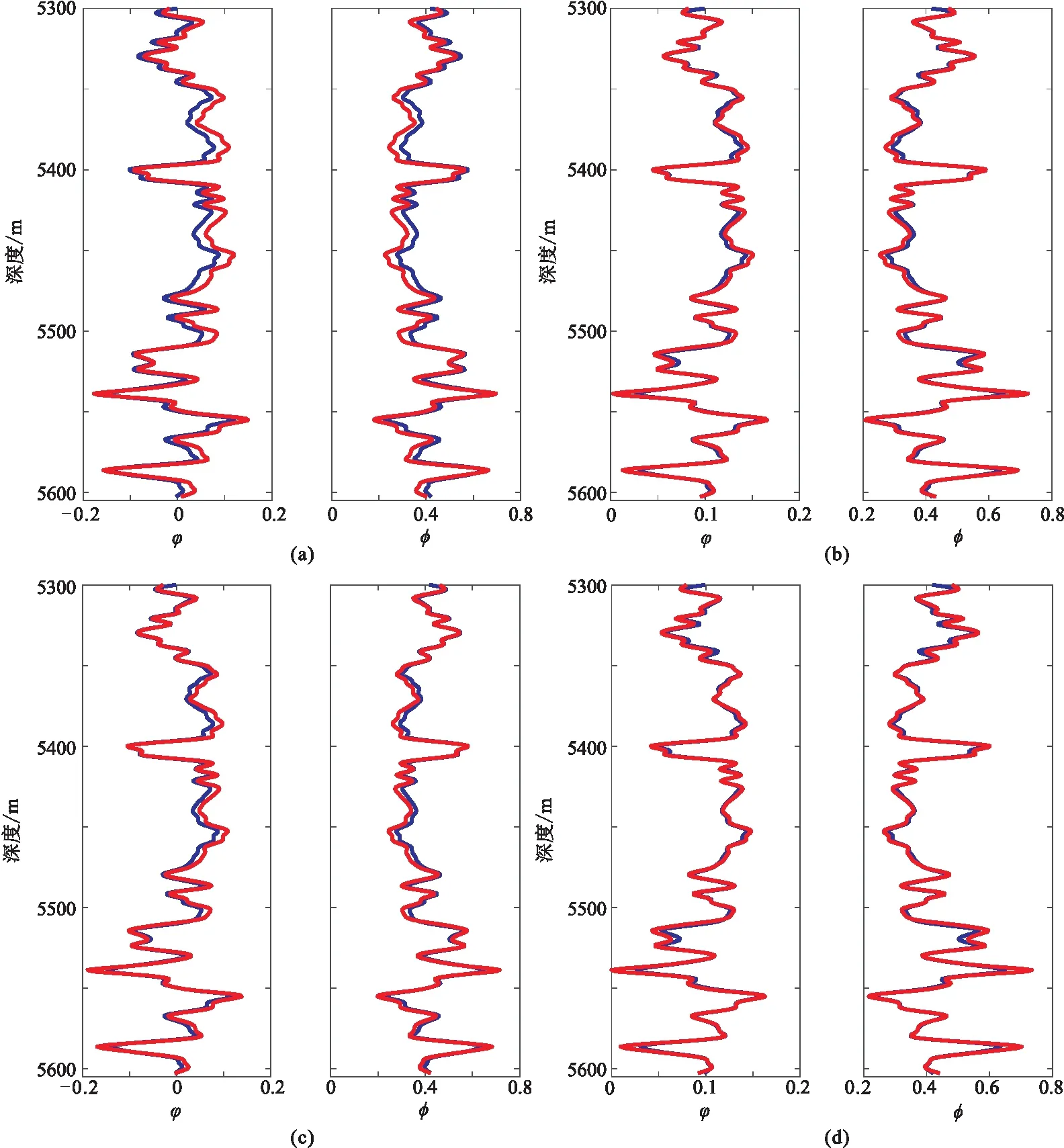
图5 一维模型孔隙度迭代反演结果(a)第一次迭代(由二分法得到的饱和度均值为0.500)； (b)第二次迭代(由二分法得到的饱和度均值为0.250)；(c)第三次迭代(由二分法得到的饱和度均值为0.375)； (d)第四次迭代(由二分法得到的饱和度均值为0.3125)红、蓝色线分别为反演曲线与模型曲线

图6 图5对应的反演结果绝对误差(a)第一次迭代； (b)第二次迭代； (c)第三次迭代； (d)第四次迭代黑色实线为误差曲线，红色虚线为0值线

图5对应的反演结果绝对误差。由图可见：随着迭代次数增加，饱和度均值趋于模型饱和度均值0.29，反演结果逐渐收敛(图5)； 孔隙度、泥质含量反演结果绝对误差接近0(图6)，并且收敛速度较快，2～4次迭代即可得到最优解。上述结果说明所提迭代反演方法可行、有效。

3 实际应用

M区位于塔里木盆地北部凹陷，研究目标为底水块状油藏，埋深大于5000m，目的层为砂岩储层，厚度约为100m，以滨岸相沉积为主。储层物性相对均匀，且地震资料品质较好，适合孔隙度迭代反演测试。该区W1井测井序列相对完整，包含纵、横波速度及密度数据，通过计算可得到孔隙度、泥质含量及饱和度。以W1井数据为基础进行岩石物理建模，选用适合砂岩储层的Xu-White模型[16]。

图7为M区岩石物理模型正演结果，可见实测曲线与正演结果较吻合，证明所建岩石物理模型有效。通过岩石物理建模，确定M区砂、泥岩组分孔隙横纵比分别为0.190、0.008，岩石物理基本建模参数如表1所示。

表1 各组分岩石物理基本参数

基于岩石物理建模结果，结合叠前同步反演得到的纵、横波速度等弹性参数，并将饱和度分别为1和0的初始含水饱和度模型作为输入，进行迭代反演，求取孔隙度与泥质含量(图8)。

图8为M区孔隙度与泥质含量迭代反演剖面。由反演结果可见一条高泥质含量条带(图8b)，且对应位置的反演孔隙度出现明显低值区(图8a)，稳定泥岩段上覆于巨厚块状砂体之上，与钻井成果及地质认识相吻合。因此，反演结果较好地表征了目的层段储盖组合。为了进一步验证反演效果，提取井点位置的反演曲线进行分析。

图9为W1、W2井井位处目的层段反演结果。由图可见，孔隙度、泥质含量反演结果与实测曲线的相对变化规律基本一致，但二者的绝对值在局部存在差异，其原因是迭代得到的常值模型饱和度与实际饱和度的差异所致。因此，反演结果对目的层段储层物性具有一定指示作用，对于纯油层或纯水层，反演精度高，但当流体性质存在纵向分异时，反演精度有所下降。

图7 M区岩石物理模型正演结果黑色线为实测曲线，红色线为正演结果

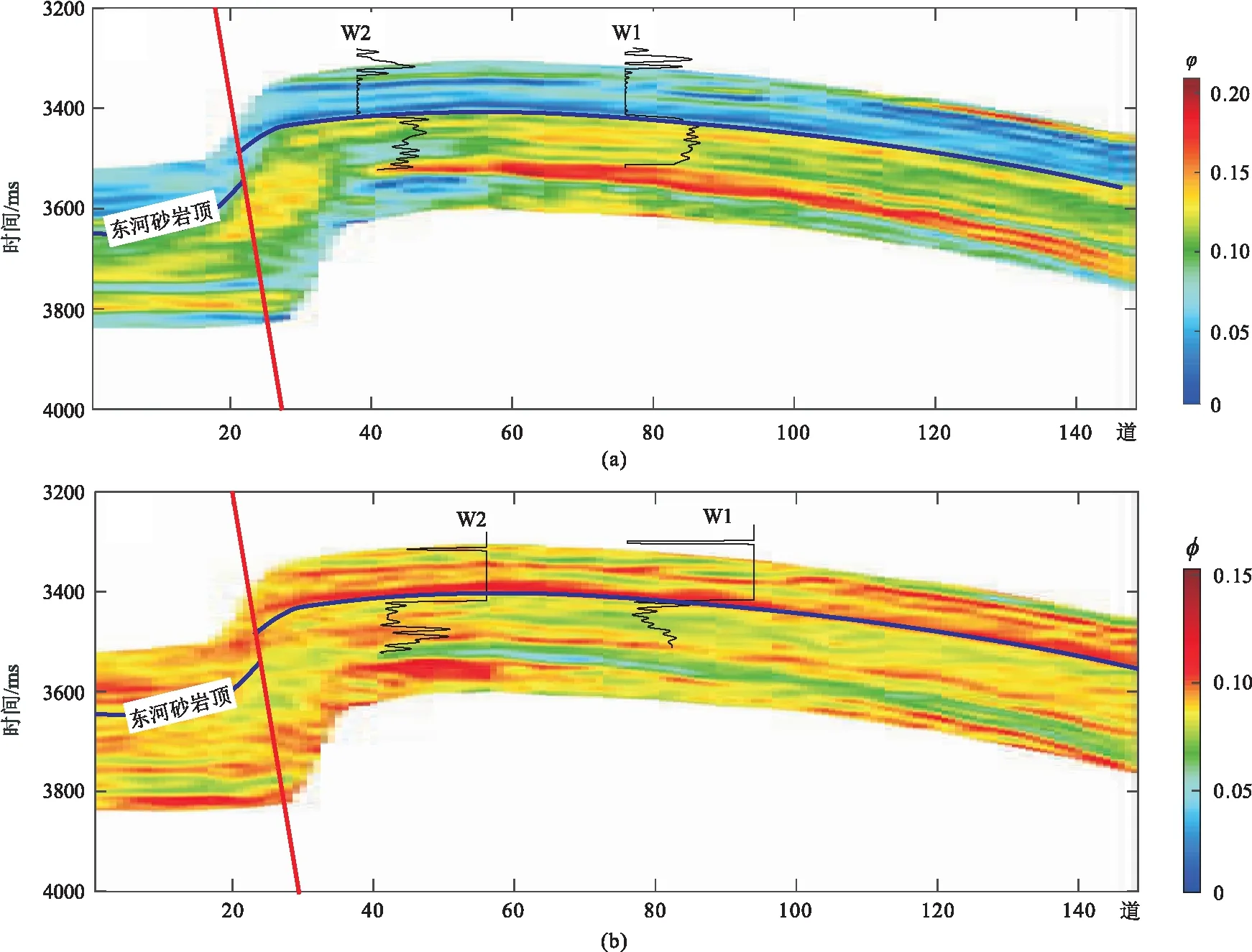
图8 M区孔隙度(a)与泥质含量(b)迭代反演剖面W2井揭示，在东河砂岩下段储层物性发生变化，泥质含量增加、孔隙度降低

图9 W1(a)、W2井(b)井位处目的层段反演结果

4 结论

本文以岩石物理线性近似模型为基础，推导了纵、横波速度与孔隙度、泥质含量的线性关系式，并基于贝叶斯理论构建反演目标函数，利用二分法求解，迭代反演了储层孔隙度、泥质含量。该方法不依赖于密度项，适用于储层深埋条件下的孔隙度预测，拓宽了岩石物理线性反演方法的适用性。理论模型与实际数据测试结果表明，所提方法具有一定可行性，且应用效果较明显。

针对油、水两相流体饱和岩石，本文方法反演结果对饱和度模型不敏感，应用迭代反演方法可以得到相对可靠的孔隙度预测结果。对于纯油层或纯水层，反演精度高，但当流体性质存在纵向分异时，反演精度有所下降。对于气层，反演结果对饱和度模型的精度要求较高，可能会降低孔隙度迭代反演方法的适用性。关于含气储层的孔隙度反演方法有待进一步研究和完善。