一种自动判定保留的奇异值个数的地震随机噪声压制算法

朱跃飞 曹静杰* 殷晗钧

(①自然资源部京津冀城市群地下空间智能探测与装备重点实验室，河北石家庄 050031； ②河北省战略性关键矿产资源重点实验室，河北石家庄 050031)

0 引言

受人类活动、仪器、环境、天气等多种因素影响，野外采集的地震数据往往含有各种噪声，严重影响速度分析和静校正、速度建模及偏移成像等处理的效果。因此，消除噪声以获取高信噪比地震数据一直是地震勘探面临的难题[1]。地震数据去噪一般依赖信号和噪声在频率、统计规律、振幅等方面的差异分离信号和噪声。地震噪声分为随机噪声和相干噪声。地震随机噪声的消除方法众多，大体上分为滤波类方法、基于变换的方法、降秩方法和深度学习方法等。

滤波类方法基于地震数据时间域分布特点构建滤波函数去除噪声，主要方法有中值滤波[2-3]、各向异性扩散滤波[4]等。基于变换的方法假设地震数据经过某个变换后的系数具有稀疏特征，选取较大的系数，通过阈值运算去掉小的系数，最后反变换到时间域实现去噪[5]，常用的变换有傅里叶变换[6]、Radon变换[7]、Wavelet变换[8-10]、S变换[11]、曲波变换[12]等。

深度学习去噪方法是目前的研究热点，基本原理是利用大量的样本数据的特征，通过多层卷积的方式提取数据的时域特征，然后采用深度学习的非线性逼近能力调整网络参数，从而建立一个复杂的去噪模型实现去噪。目前卷积神经网络[13]、残差学习[14-15]、生成对抗网络[16]、降噪自编码[17]等深度学习网络被用于地震数据去噪。深度学习方法需对不同的数据大量训练，因此计算量大。

多道奇异谱分析(MSSA)是一种基于奇异值分解的降秩去噪方法，通过奇异值分解将原始数据分解为信号子空间和噪声子空间，然后将噪声子空间的能量置为零(截断)，再通过反变换去噪[18]。MSSA用于多道时间序列分析，是单道奇异谱分析(SSA)的推广[19-20]。Read[21]率先将SSA拓展到多变量MSSA方法研究，基于线性同相轴的假设，利用相邻地震道的频谱相似性与可预测性组成低秩的Hankel矩阵[22]，噪声破坏了数据频率切片Hankel矩阵的低秩结构[23]，常用截断奇异值分解方法解决低秩近似问题。在地震信号处理领域，MSSA和Cadzow滤波是等效的但却来自不同的领域[24]，即Cadzow滤波源于信号和图像去噪，MSSA则源于分析由动力系统引起的时间序列，本文采用MSSA的名称表示这类方法。Oropeza等[25]利用MSSA同时对叠前三维数据去噪和重建，数值实验表明无法完全消除随机噪声，其去噪效果有很大的提升空间。Huang等[26]将阻尼算子引入传统MSSA中，提出了阻尼多道奇异谱分析(DMSSA)算法。通过融合软阈值移动平均算子和阻尼算子的优点，Oboue等[27]利用鲁棒阻尼降秩方法提高地震数据的信噪比。阻尼降秩方法已成为一种有效的去噪方法，可以从含噪和不完备的观测数据中恢复有效信号。

对于海量地震数据来说，基于降秩的方法需要将地震数据分成不同的块，然而每个块对应的奇异值个数不同，目前需要人工估计每个块的有效奇异值个数，计算效率低，无法实现产业化。为此，本文利用Akaike信息准则自动地确定地震信号的奇异值个数，然后基于DMSSA方法去噪。首先介绍了MSSA方法的去噪原理，然后给出确定有效奇异值个数的Akaike信息准则和经验方法，经验方法可以验证Akaike信息准则的有效性。模拟和实际数据实验表明，Akaike信息准则能够自动确定有效奇异值个数，避免了人工操作，有利于实现产业化。

1 算法原理

1.1 DMSSA方法[18]

假设一个含噪三维地震数据为D(x,y,t)，其中x=(x1,…,xm)、y=(y1,…,yn)表示空间坐标，t=(t1,…,ts)表示时间坐标，m、n为道数，s为采样点数。根据DMSSA理论，使用以下步骤去噪。

(1)通过离散傅里叶变换将D(x,y,t)从时间域变换为频率域数据F(x,y,ω)，其中ω=(ω1,…,ωj)为离散的频率序列，j为频率切片个数。

(2)在给定的频率范围内将不同频率切片数据排列成块Hankel矩阵。当频率为ωi(i=1,…,j)时，有

(1)

首先，将F(x,y,ωi)的每一行构造成Hankel矩阵

(2)

Rk表示由F(x,y,ωi)的第k行构造的Hankel矩阵，大小为v×h，v=

n/2

+1，h=n-v+1，

·

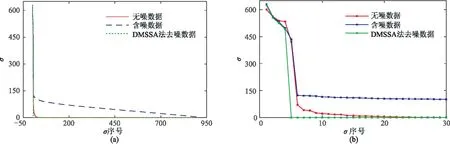
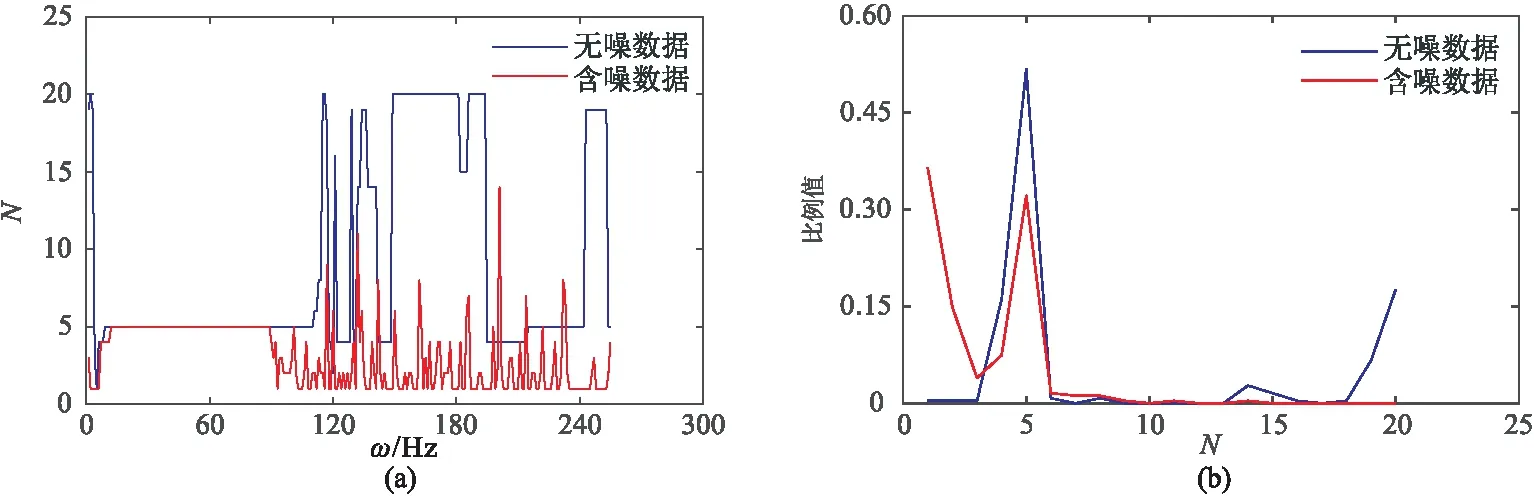
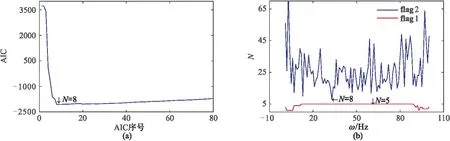
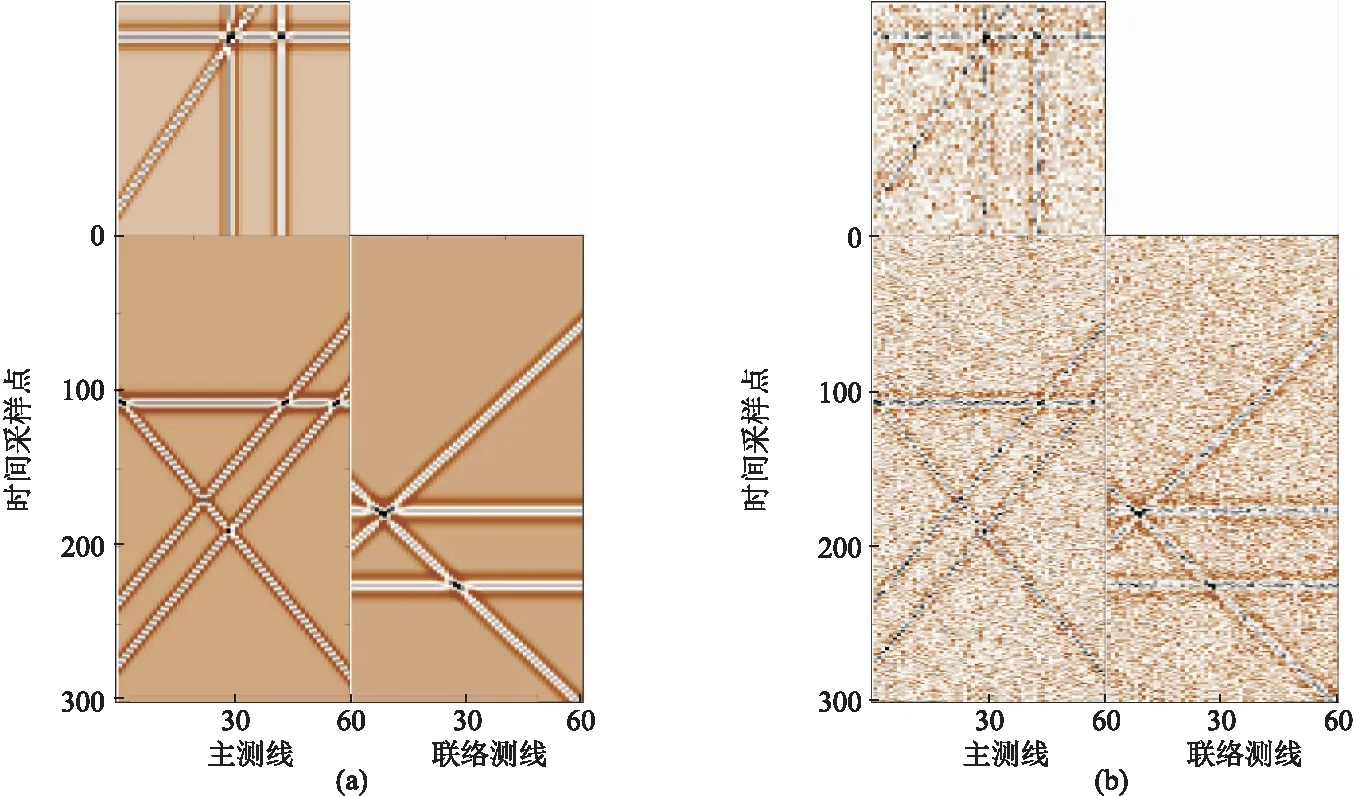
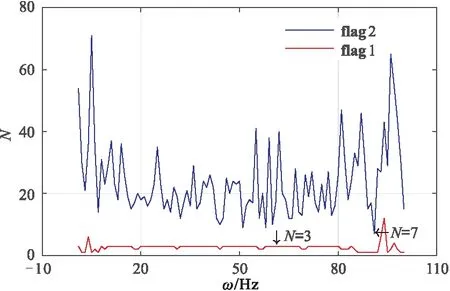
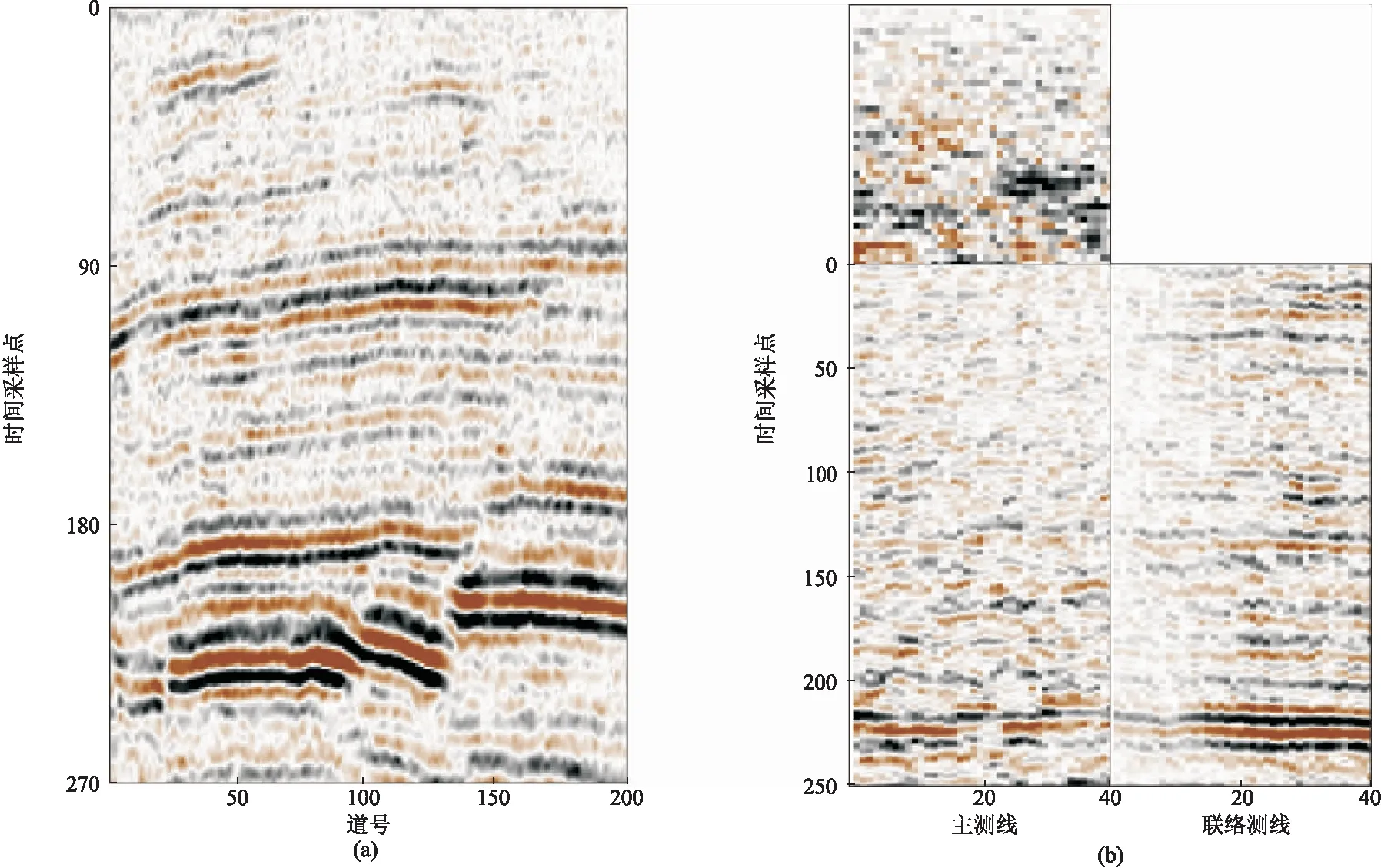
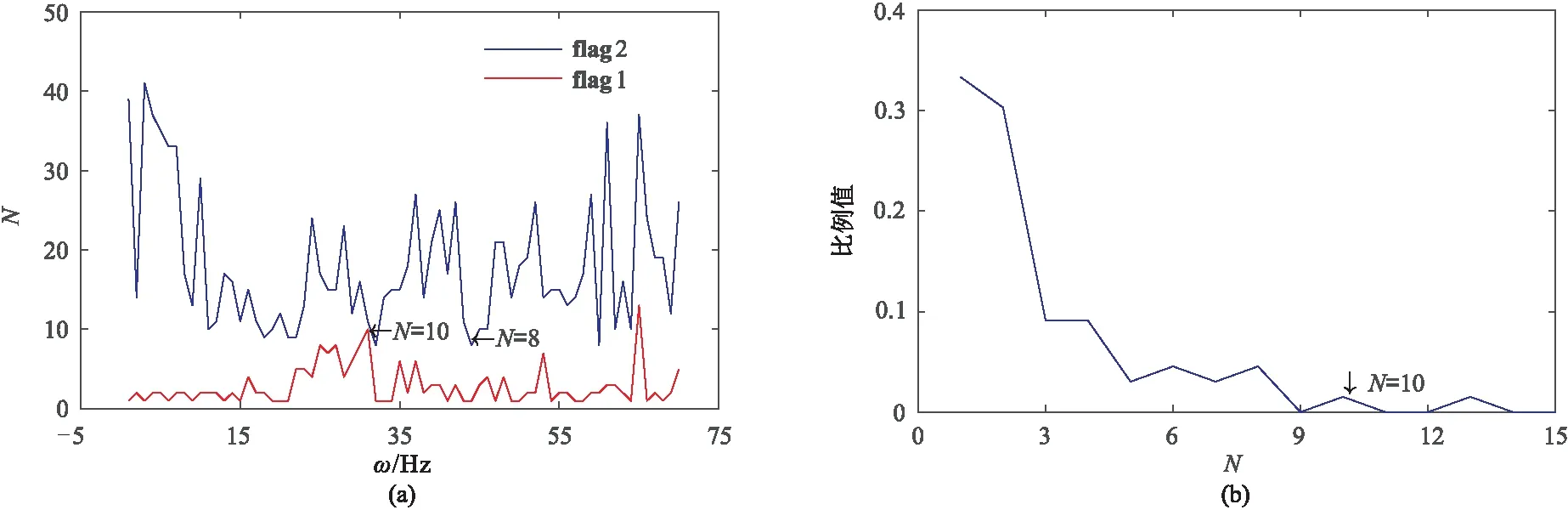
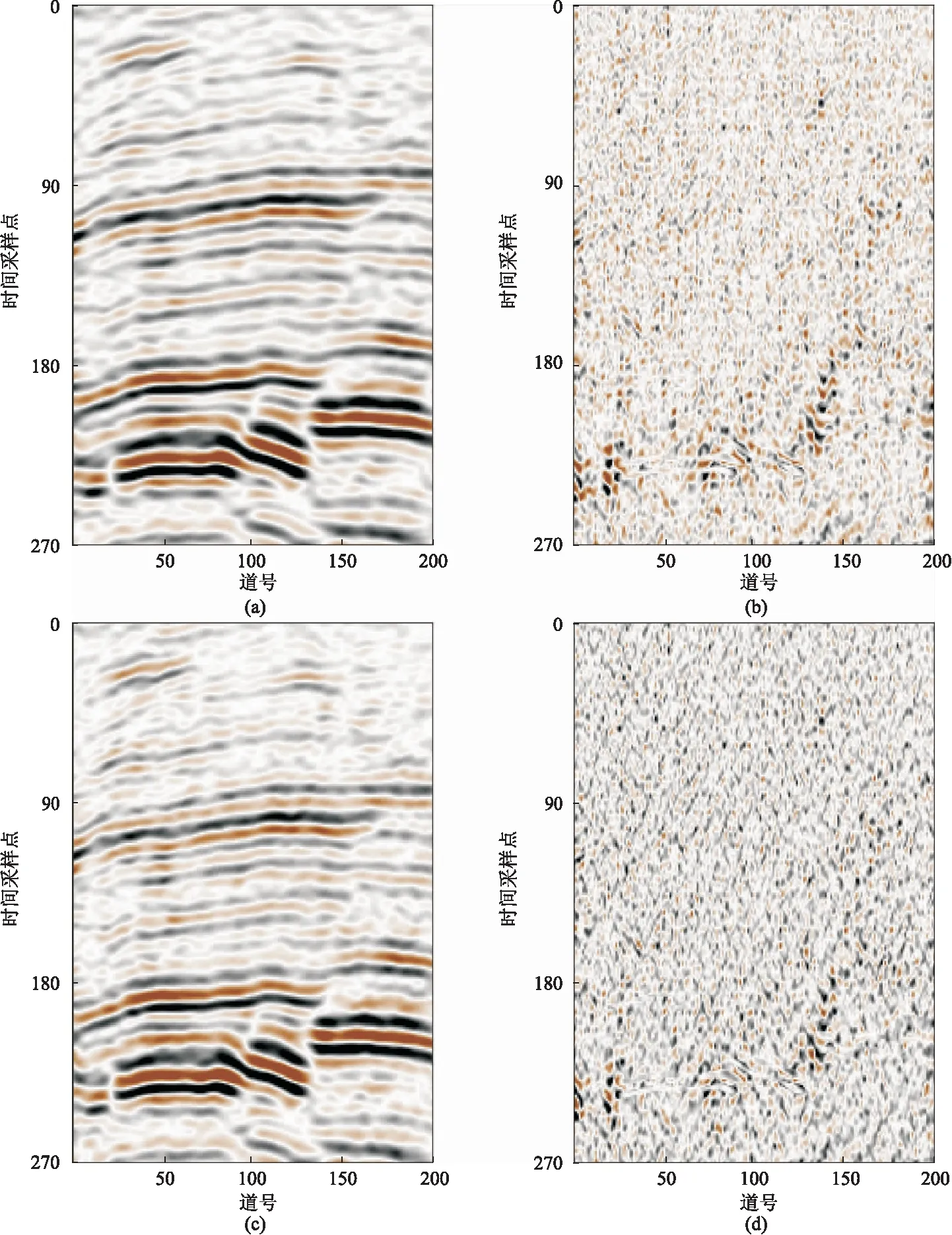
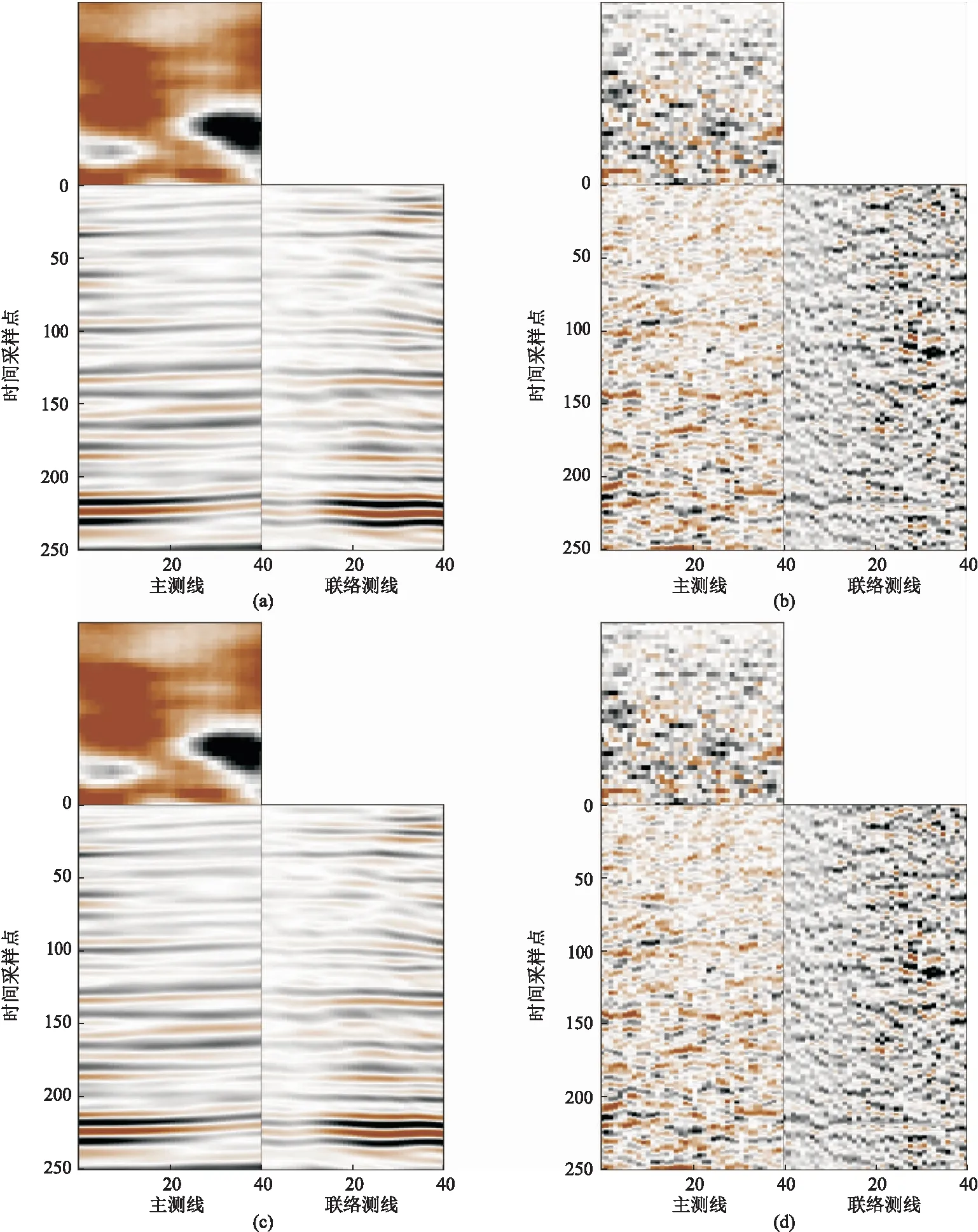
表示向下取整，其中2

(3)

H为(v×l)×(h×f)阶块Hankel矩阵，l=

m/2

+1，f=m-l+1，2

(3)对H进行奇异值分解，并且选择和截断奇异值，是MSSA类方法的关键。如果有效信号对应的奇异值个数为N，则奇异值对角矩阵仅保留前N个奇异值，而其他所有奇异值均设置为零。对H进行奇异值分解，得到

(4)

其中

(5)

式中：U为H的左奇异值向量组成的(v×l)×(v×l)阶正交矩阵；VT为H的右奇异值向量组成的 (h×f)×(h×f)阶正交矩阵；Σ为按奇异值递减顺序σ1≥σ2≥…≥σd组成的对角矩阵，非零奇异值的个数d等于H的秩。

(4)基于截断的奇异值计算去噪结果。通过将Hankel矩阵反变换到频率域，再通过离散傅里叶逆变换得到时间—空间域去噪地震数据，即

Σ1=diag(σ1,σ2,…,σN) 0≤N

(6)

(7)

对所有的频率域数据进行上述操作即可得到去噪地震数据。

若采集的地震数据中不含噪声，则Σ仅包含与有效信号相关的非零σ。若采集的地震数据中含有噪声，所有σ都会发生改变，非零σ的个数也将增加。原始MSSA方法仅保留了N个σ，对σ的大小并没有影响，因此去噪结果有很大的改进空间。Huang等[18]提出的DMSSA方法可以减小σ，因此去噪效果更好。

DMSSA方法通过添加阻尼因子减弱由噪声引起的σ增量，即

(8)

(9)

式中：T为阻尼算子；I为单位矩阵；D为阻尼因子，其值越小，阻尼效果越强，反之亦然。DMSSA去噪的本质就是利用D对第N+1个σ放大或缩小，然后使用前N个σ与其求差，并对第N+1之后的σ置零，以达到压制噪声的目的。

确定N是DMSSA去噪最关键的一步，将影响噪声抑制效果和有效信号的保护程度。式(4)和式(9)是假定N已知的情况得到的，如果选择N太小，将损坏有效信号； 如果选择N太大，将降低噪声压制效果。对于MSSA类方法，自动确定N是关键。面对复杂多变的实际地震数据，在没有充足的地质资料时，确定数据块中需要保留的N是一个值得研究的问题。实际数据去噪时要对数据分块，需要人工估计每个块的有效N，计算效率低，无法实现产业化。为此，首先引入一种确定有效N的经验估计方法，然后给出了一种自动确定N的方法，该方法基于Akaike信息准则自动确定有效N，有利于MSSA产业化。

1.2 经验公式法

图1为模拟地震数据A三维视图。模拟数据使用主频为40Hz的雷克子波作为震源，信噪比(SNR)定义为

图1 模拟地震数据A三维视图(a)无噪数据； (b)加入10%随机噪声数据(信噪比为-1.322dB)数据含有5个不同倾角的地震同相轴，时间方向有300个采样点，采样率为2ms，主测线和联络测线方向均为60个采样点

(10)

式中：d为不含噪数据；r为去噪后数据。

图2为图1数据在ω12处的σ曲线。由图可见，地震数据在无噪声时仅出现少数较大的σ且个数为N，其他σ均较小，因此σ曲线出现明显的弯折现象(图2b红线)。从理论上来说，无噪时N以后的σ应该全部为零。数据加入噪声后，σ发生改变的同时也出现大量非零σ，因此加噪后的σ曲线下降相对平缓，但在第N和第N+1项之间，依然存在巨大的落差。

通过区分数据含噪和不含噪情况的σ，从而确定数据块中要保留的N。基于错位相除的思路，提出一种确定数据块中有效N的经验估计方法。首先将Σ的σ排列成新的向量

Q=(σ1,σ2,…,σd)

(11)

对Q错位相除，得

(12)

定义新的向量

Q′=(q1,q2,…,qd-1)

(13)

式中Q′是基于Q的元素错位相除构造的新向量，其第i个元素等于Q的第i+1个元素除以第i个元素。若σi和σi+1的值较接近，则qi的值趋于1，否则将出现一个较小的值。对Q′取极小，并获取极小值对应的索引，有

N=arg minQ′=(q1,q2,…,qd-1)

(14)

在实际处理中，只需截取Q′的前若干项即可。图3为错位相除向量曲线。由图可见，Q′的第5个元素值明显小于第4个元素和第6个元素，说明在该频率下应该保留5个奇异值(图3b)。

为了排除偶然性，使用上述方法对数据块的主频数据进行相同的计算，并得到新向量

flag1=(arg minQ′ωL,…,arg minQ′ωH)

(15)

其中ωL～ωH为信号的主要频率范围。通过统计flag1中不同的N出现的占比，根据经验选择合适的N。图4为由经验公式法确定的图1a的σ分布。由图可见：不论是否含有噪声，在主频范围内N均为5(图4a)； 含噪声数据和不含噪声数据N=5的占比分别为0.5、0.35，故确定N为5(图4b)。因此，无论数据中是否包含噪声，利用经验公式法均可准确估计N。经验公式法所用的错位相除策略和一阶差分具有异曲同工的效果，可以验证其他方法的效果，为确定N提供了有效工具。

图2 图1数据在ω12处的σ曲线(a)全部σ分布； (b)图a前30个σ分布局部放大

图3 错位相除向量曲线(a)完整曲线； (b)图a前10项元素的局部放大

图4 由经验公式法确定的图1a的σ分布(a)全频率扫描结果； (b)统计结果

1.3 ADMSSA算法

处理海量地震数据时需要分块地震数据，然后对每个数据块去噪。但是每个数据块对应的N并不相等，人工预估方法不利于算法实施，因此需要研究自适应算法。

对σ序列Q可依据第N和第N+1个σ之间的巨大落差并伴随严重的弯折现象确定有效N。事实上，N值的选择就是检测σ序列中的拐点位置。本文利用Akaike信息准则[28-29]自动判定保留的N。首先对Q作如下变换

fωi(σμ)=σμ+1-2σμ+σμ-11≤μ≤d

(16)

式(16)实际上是求σ序列曲线的二阶导数，fωi(σμ)描述σ曲线斜率的变化率。确定频率为ωi、第R点的有效N值的Akaike信息准则为

AICωi(R)=Rlg[var(fωi[σi,σR])]+

(d-R-1)lg[var(fωi[σR+1,σd])]

(17)

式中：var表示数据序列的方差； AICωi(R)是长度为d的序列，其全局最小值对应的位置即为拐点，按

flag2=(arg minAICωL,…,arg min AICωH)

(18)

求出所有频率中的最小值。式(18)中元素最小值即是整个数据块中需要保留的N。图5为由ADMSSA算法确定的图1a的σ分布。由图可见：①在N=8时AICωi(R)曲线取极小值(图5a)。由于主频范围内数值结果较稳定，其他范围则经常出现异常值，为了提高精度将频率控制在10～90Hz内。②ADMSSA算法确定的N为8(图5b)，经验公式法确定的N为5(图4b)，证明利用基于Akaike信息准则的方法去噪，可以自动地估计出与真实值较接近的N。

在使用上述方法确定N后，去噪过程采用DMSSA方法的框架，在ADMSSA算法中仅需要确定信号的主频范围，就可以自动地去噪。

图5 由ADMSSA算法确定的图1a的σ分布(a)信息准则曲线； (b)信息准则确定的结果

2 数值实验

2.1 模拟数据实验

分别使用ADMSSA、DMSSA方法对图1b去噪，结果(图6)表明：由ADMSSA、DMSSA方法确定的N分别为8、5，令阻尼因子D=3，去噪结果的信噪比分别为22.110(图6a)、22.438dB(图6c)，两者的去噪效果较接近，信噪比较高，同相轴清晰连贯，局部细节得以保留。

图6 图1b的去噪效果对比(a)ADMSSA方法去噪结果； (b)ADMSSA方法去除的噪声； (c) DMSSA方法去噪结果； (d) DMSSA方法去除的噪声

图7 模拟地震数据B三维视图(a)无噪数据； (b)加入15%随机噪声数据(信噪比为-4.659dB)数据含有4个不同倾角的地震同相轴，时间方向有300个采样点，主测线和联络测线方向均为60个采样点，采用主频为40Hz的雷克子波正演

能量较强的噪声经常使地震信号发生严重畸变，导致块Hankel矩阵σ变化复杂。为了验证ADMSSA方法的有效性和对噪声的敏感程度，对含噪地震数据(图7b)去噪，结果表明，DMSSA方法确定的N为3(图8红色实线)，ADMSSA方法确定的N为7(图8蓝色实线)。

图9为图7b的去噪效果对比。由图可见，令阻尼因子D=3，ADMSSA、DMSSA方法去噪结果的信噪比分别为21.263(图9a)、21.778dB(图9c)，即前者的信噪比略低，但去噪结果的同相轴清晰，噪声残留较少(图9b)，说明ADMSSA方法高效、精确。

2.2 实际地震数据实例

为了证明ADMSSA算法对实际地震数据的去噪效果，分别使用二维和三维叠后地震数据(图10)验证。二维地震数据(图10a)信噪比低，地震同相轴连续性差，随机噪声能量强，剖面中间部分以及下部存在断层，尤其是下部存在多处断裂构造。三维地震数据(图10b)信噪比低，噪声能量较强，有效信号被噪声严重污染，中间部分同相轴出现弯曲、断裂现象。

图8 两种方法对图7b数据确定的N

图9 图7b的去噪效果对比(a)ADMSSA方法去噪结果； (b)ADMSSA方法去除的噪声； (c)DMSSA方法去噪结果； (d)DMSSA方法去除的噪声

图11为图10a的σ分布。由图可见：ADMSSA方法确定的N为8(图11a蓝色实线)； DMSSA方法统计N出现的百分比(图11b)确定的N为10。图12为二维地震数据去噪效果对比。由图可见，令阻尼因子D=5，地震同相轴边缘刻画清晰，噪声去除彻底，对构造细节保护较好，去噪效果均较好。图13为图10b的σ分布。由图可见：ADMSSA方法确定的N为5(图13a蓝色实线)； DMSSA方法统计N出现的百分比确定的N为4(图13b)。

图14为三维地震数据去噪效果对比。由图可见，两种方法去噪结果基本相同，无论是在地下结构较稳定区域还是在断点附近，ADMSSA方法的去噪结果很好地保护了构造细节(图14a)，同相轴的轮廓清晰，去噪效果很好。

图10 二维(a)、三维(b)地震数据

图11 图10a的σ分布(a)DMSSA、ADMSSA方法确定的N； (b)DMSSA方法统计结果

图12 二维地震数据去噪效果对比(a)ADMSSA方法去噪结果； (b)ADMSSA方法去除的噪声； (c)DMSSA方法去噪结果； (d)DMSSA方法去除的噪声

图13 图10b的σ分布(a) DMSSA、ADMSSA方法确定的N； (b)DMSSA方法统计结果

图14 三维地震数据去噪效果对比(a)ADMSSA方法去噪结果； (b)ADMSSA方法去除的噪声； (c)DMSSA方法去噪结果； (d)DMSSA方法去除的噪声

3 讨论

对于MSSA类方法来说，划分的数据块的尺度对计算时间和去噪效果均有影响。ADMSSA方法同样受到划分数据块尺度的影响，因此在划分数据块时应先做试验，再确定划分尺度。ADMSSA方法需要选择一个合适的频率范围，一般取信号有效频率范围即可取得较好去噪结果。DMSSA方法受阻尼因子D的影响，当噪声能量较强时，选择D约为3，当噪声信号较弱时，应选择较大的D值。ADMSSA方法对强脉冲噪声具有一定压制作用，但是去噪结果中仍残存一些强脉冲噪声。MSSA方法对奇异值个数N依赖很强，当N较小时，会影响断层的识别。对于曲率较大的弯曲同相轴，需要合理划分数据块尺度。MSSA方法的计算量主要为奇异值分解，为了提升算法的计算效率，可以采用随机奇异值分解等方法。

DMSSA方法和ADMSSA方法确定的N存在差别，这是由于前者依靠经验公式法估计N，存在一定误差，而ADMSSA方法依靠数据信息通过概率分析提取信号特征。

降秩类去噪算法在消除随机噪声的同时会对有效信号造成一定损伤，其原因是该类方法基于线性同相轴假设，实际数据很难满足条件。因此，尽管降秩类去噪算法获得了较好效果，但是去噪效果尚有很大的提升空间。

4 结论

对于MSSA类去噪方法来说，确定有效的奇异值个数是关键。目前都是依靠人工经验估计奇异值个数，不利于该类方法的产业化。本文提出了一种确定有效奇异值个数的方法，该方法基于Akaike信息准则自动区分有效信号对应的奇异值与噪声相关的奇异值，克服了人工选择奇异值个数的问题，有利于海量地震数据去噪。此外，本文还提出利用经验公式法验证ADMSSA方法的可靠性。数值实验证明，ADMSSA方法能够自动地确定可靠的奇异值个数，并且获得高信噪比的去噪结果，该算法在工业化应用中具有巨大潜力。