基于BIM技术的大型铸钢节点管桁架吊装分析

赵 锋，甘聪颖，胡康翔，金仁才，陶清林，贾冬云(.中国十七冶集团有限公司；. 安徽工业大学 建筑工程学院 安徽马鞍山 4300)

大跨度空间管桁架的单榀、分段吊装和整体提升等施工技术的应用和研究，保证了施工阶段的结构安装精度[1]、[2]。大型管桁架的吊装模拟分析，对结构的强度、温度响应和稳定性能进行研究，查找薄弱环节，保障了施工安全[3]、[4]。BIM技术在大跨度钢结构的虚拟仿真施工中的应用，提高了吊装方案的合理性，丰富了BIM技术的应用理论[5]-[9]。有限元软件在大型吊梁的仿真分析和优化设计中也起了重要作用，不仅避免吊装失稳，也降低施工成本[6]。本文选取两榀典型的管桁架，采用Tekla和ABAQUS软件创建模型，引入大型铸钢节点的相关参数，获取单榀管桁架的起吊中心，并进行受力分析，根据结构应力和变形情况，判断吊点的合理性，指导现场吊装作业，提高吊装效率和施工安全。

1 工程概况

某大型体育场上部大悬挑钢结构屋盖为马鞍型挑篷，平面投影近椭圆形，东西向最大悬挑长度为39.2 m。管桁架断面为倒三角形，钢管材质为Q345B，铸钢节点材质为G20Mn5QT。上弦规格为Ø351×16 mm、Ø450×16 mm、Ø550×30 mm，下弦杆规格为Ø351×16 mm、Ø325×12 mm，腹杆规格为Ø180×8、Ø219×10、Ø273×12每榀桁架均配有4个铸钢节点，节点编号见图1。

图1 典型单榀管桁架立体示意图

采用500 t履带吊，配一台200 t履带吊配合，位于场内顺时针方向单榀吊装。施工中采用双根Ø46钢丝绳捆绑吊点处，并以37吨卡环固定。在较大悬挑端设置2根Ø16钢丝绳，稳定桁架吊装过程中的姿态(见图2)。

图2 单榀管桁架起吊

2 基于BIM技术的单榀管桁架吊点位置选择

为了精确获得单榀管桁架的重心和吊点位置，利用BIM技术建立屋盖结构的整体模型，得到每榀桁架模型的终位形，即起吊时的初始位形，再获取重心位置，合理选择吊点，指导吊装作业。本文采用Tekla和ABAQUS分别计算两榀典型管桁架ZHJ10和ZHJ21的重心，根据重心点选择吊点位置，并应用ABAQUS分析关键构件的受力状态，确保桁架吊装状态接近最终设计状态。

2.1 基于Tekla模型的起吊中心确定

Tekla Structures软件能快速完成构件多、节点量大复杂的钢结构模型建造和加工图纸的绘制。应用其确定管桁架起吊中心的具体操作步骤如下：

1)确定管桁架起吊位形：根据结构设计图建立屋盖结构的Tekla整体模型(见图3a)，得到每榀桁架模型的终位形，即起吊时的初始位形。

2)建立铸钢节点模型：根据每个铸钢节点设计图以及其真实重量mi和重心，调整模型中铸钢节点处的相关截面参数，如管壁厚度、变空心管为实心管，确保铸钢节点重心位置的精确性(见图3b)。

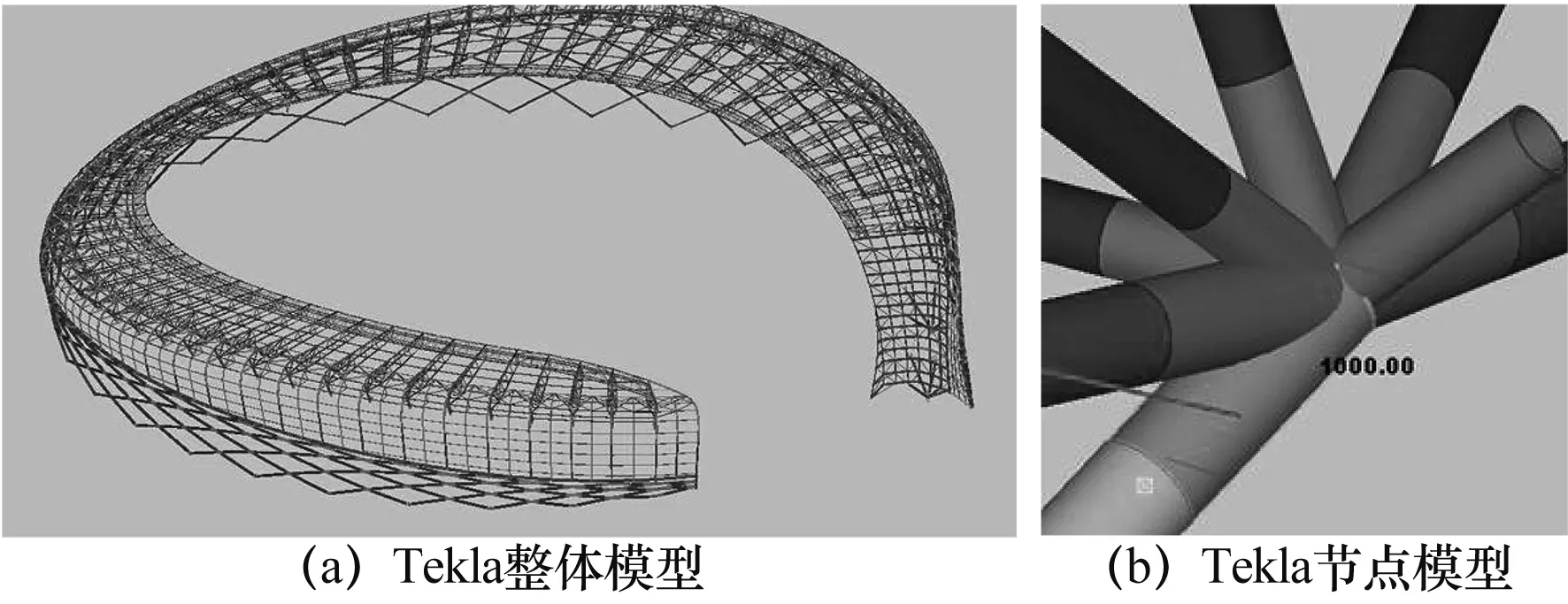
图3 Tekla建模

3)定位起吊中心：查询每榀管桁架的重量即为实际加工成品重量M0；查询其重心位置坐标，输入同坐标系的AutoCAD三维模型中，并将重心点向上做垂线与上弦杆轴线相交，可得吊点的中心(见图4)。

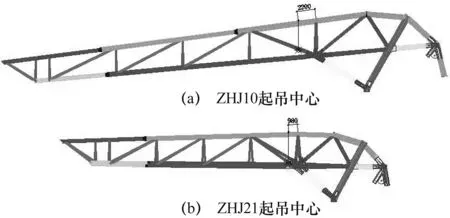
图4 两榀管桁架起吊中心(AutoCAD模型)

ZHJ10和ZHJ21实际重量M0见表1，起吊中心距右侧竖腹杆的距离l1见图4a和b，数据列入表2。

2.2 基于ABAQUS模型的起吊中心确定

应用ABAQUS确定管桁架起吊中心的具体操作步骤如下：

1)按照实际重量M0调整ABAQUS模型重量：将管桁架AutoCAD三维模型导出的igs文件以梁单元形式导入ABAQUS模型，定义所有构件的截面和材料方向，查询模型初始质量M1，将各铸钢节点重量mi以质点形式施加到相应节点处(见图5a)，再次查询得到模型质量M2。

图5 管桁架ABAQUS分析模型

因为M2中节点处的重量是原相贯节点重量与铸钢节点之和，使得M2比Tekla模型重量M0(即是实际结构重量)大，必须将二者的差值消除，才能使ABAQUS模型的重量与实际结构一致。因此，将M2减去计算净重M0得到节点的总附加质量差值M3，将其按各铸钢节点重量进行分配，得到每个铸钢节点的附加质量Δmi。以Δmi替换模型中的mi，得到最终模型质量M4，其值与实际质量M0相同。两榀管桁架有限元模型重量调整过程见表1。

表1 管桁架ABAQUS模型重量调整表

2)确定管桁架重心和起吊中心：查询质量属性获得管桁架重心坐标，并创建重心和通过重心的YZ平面，该平面与上弦的交点是重心沿Z轴在上弦杆的投影位置，即为起吊中心。ZHJ10和ZHJ21起吊中心距右侧竖腹杆节点尺寸l2及其与Tekla模型l1的比较见表2。

表2 两种模型的管桁架起吊中心及偏差

3)确定吊点参考位置：在起吊中心的两侧一定范围内创建两个吊点平面，以此平面与上弦杆相交创建两个边缘点，即为两个吊点参考位置(见图5b)。吊点的具体位置必须依据下述的有限元分析结果进行确定。

3 管桁架吊装有限元分析

3.1 管桁架吊装分析模型和参数

利用上述管桁架的ABAQUS模型，定义材料为Q345B热轧无缝钢管，容重为7850 kg/m3，弹性模量为206 GPa，泊松比为0.3，重力加速度为9.8 m/s2。钢材本构模型采用理想线弹性本构模型。将腹杆定义为杆截面(Truss)，赋予截面面积；其余杆件按照梁截面(Beam)赋予钢管半径和壁厚。

在每榀管桁架起吊中心的两侧一定范围内选取两个吊点，并设置三向约束支座模拟起吊时钢丝绳卡环固定约束。对整个模型施加重力荷载，并按照表1数据将铸钢节点重量Δmi作为竖向集中力施加到相应节点上(见图5b)。

竖腹杆和斜腹杆为T3D2杆单元，其余杆件均为B31梁单元。

3.2 管桁架吊装分析

为了防止吊装失稳，整个起吊、移动和就位过程缓慢，故采用静态线性摄动分析法对两榀管桁架的受力性能进行计算。ZHJ10和ZHJ21的吊点均选在起吊中心的±400 mm处，竖向变形和轴向应力云图见图6和图7。

图6 ZHJ10轴向应力和竖向变形云图 图7 ZHJ21轴向应力和竖向变形云图

由两榀管桁架的变形和应力情况可知：(1)所有节点的竖向变形均为向下变形，没有出现悬臂端上翘现象，说明结构处于整体平衡状态。最大竖向变形均出现在左悬臂端(ZHJ10的21号节点和ZHJ21的25号节点)。(2)吊点左侧的上弦杆1(ZHJ10的40号杆、ZHJ21的25号杆)和右侧的上弦杆2(ZHJ10的38号杆、ZHJ21的23号杆)，以及左侧的斜腹杆1(ZHJ10的34和46号杆、ZHJ21的20和32号杆)和右侧的竖腹杆1(ZHJ10的7和37号杆、ZHJ21的7和22号杆)拉应力较大，吊点右侧的斜腹杆2处(ZHJ10的41和58号杆、ZHJ21的26和34号杆)压应力较大。

将关键杆件的轴向应力、竖向变形最大值列入表3。由表中数据可知：1)ZHJ10和ZHJ21最大竖向变形分别为25.25 mm和18.37 mm，均出现在左侧悬臂端，分别约为悬挑长度的1/1440和1/1280，满足变形要求；2)上、下弦杆为梁单元，杆件出现局部弯曲，上、下表面应力不同，ZHJ10和ZHJ21的最大拉应力均出现在上弦杆1的上表面，下弦杆1的下表面最大压应力较大。3)竖腹杆和斜腹杆为杆单元，杆件仅有轴向力，竖腹杆1的拉应力较大，斜腹杆2的压应力最大。4)杆件中的应力均小于材料的强度设计值305 MPa，满足截面强度要求。

表3 两榀管桁架吊装有限元计算结果

4 结论

通过应用BIM技术建立管桁架模型，并依据大型铸钢节点的设计参数对模型进行修正，获取起吊中心；应用有限元分析吊装时管桁架的受力性能，并判断吊点位置的合理性，得到以下结论：

(1)考虑铸钢节点与普通相贯节点的区别，分别采用Tekla和ABAQUS两种软件建模，并调整相关节点参数，得到的单榀管桁架起吊中心偏差很小，均可以作为吊点位置选取的参考数据；

(2)判断吊点的合理性方法是：在起吊中心附近初选吊点位置，经过有限元分析所得各节点的变形均为竖向向下，保证结构的整体平衡，并且变形值满足规范要求；关键构件的最不利应力值均小于材料强度设计值。

(3)按照吊装分析方法计算所得两榀管桁架的吊点位置合理，管桁架的受力性能满足规范要求。