广义拉盖尔多项式的递推关系
孙民敬,潘 颢
(南京财经大学 应用数学学院,江苏 南京 210023)
初等数论中有关特殊函数的研究,一直以来是数论学家研究的重要课题之一.而特殊函数中的拉盖尔(Laguerre)多项式依据Gamma分布密度函数的正交多项式在物理的量子力学, 统计和数学其他学科等方面有着非常重要的应用.对n≥0 拉盖尔多项式Ln(x)定义为
(1)
前几项的拉盖尔多项式为
首先,Ln(x)是拉盖尔微分方程
(2)
的一个标准解.其次,拉盖尔多项式还是重要的正交多项式, 其满足正交关系
(3)
我们知道, 拉盖尔多项式的生成函数为
(4)
由(4)不难得到, 拉盖尔多项式可以表示成组合和的形式:
(5)
特别地, 拉盖尔多项式满足一些递推关系.例如, 对n≥1, 有
(n+1)Ln+1(x)=(2n+1-x)Ln(x)-nLn-1(x).
(6)
另一个涉及导数的递推关系是
(7)
关于拉盖尔多项式的更多性质及其在数学物理中的应用, 可以参见文献[1].
2016年,T.Kim、D.S.Kim、Hwang[2]与Seo借助微分方程, 给出了拉盖尔多项式的一个新的递推关系.对非负整数m, 定义a0(m)=m!.而对j≥1, 定义
2k-2)ik-1
这里的(x)n:=x(x-1)…(x-n+1).T.Kim等人证明,对n≥0与m≥1, 有
(8)
递推关系式(8)的优点在于, 可以利用下标较小的Ln-m(x),Ln-m+1(x), …,Ln(x)表示出下标较大的
Ln-m(x).
另一方面,拉盖尔多项式的一个自然且重要推广形式是广义拉盖尔多项式.对k≥0, 定义
(9)

xy″+(k+1-x)y′+ny=0
(10)
的标准解.已知广义拉盖尔多项式的生成函数为
(11)

首先,我们要介绍一下系数aj(m,k).对1≤j≤m定义
此外, 定义a0(m,k)=(m+k)m.本文中, 我们的主要结果如下

(12)
在本文的余下部分, 我们将给出定理的证明.先给出一个关键性引理.
1 关键引理与定理的证明
固定x, 定义
(13)
容易验证g(t)满足微分方程

一般地, 我们给出证明定理的关键引理.
引理对任何m≥1,我们有
(14)
证明我们把g(t)的m阶导数写成如下形式
显然我们只要证明
bj(m,k)=aj(m,k)
(15)
即可.
现在


由此可以推出bj(m,k)满足递推关系
b0(m+1,k)=(k+1+m)b0(m,k),
(16)
bm+1(m+1,k)=-bm(m,k),
(17)
bi-m-1(m+1,k)=(k+i)bi-m-1(m,k)-bi-m-2(m,k).
(18)
这里m+2≤i≤2m+1.
显然递推关系式(18)可以改写成
bj(m+1,k)=(k+m+j+1)bj(m,k)-bj-1(m,k).
(19)
这里1≤j≤m.因此我们有
bj(m+1,k)=-bj-1(m,k)+(m+j+1+k)bj(m,k)
=-(bj-1(m,k)+(m+j+1+k)bj-1(m-1,k))+(m+j+1+k)(m+j+k)bj(m-1,k)
注意到根据(17), 有bj(j,k)=-bj-1(j-1,k), 这样我们得到
(20)
另一方面,根据aj(m,k)的定义, 显然对j≥2, 我们有
将m换成m+1得到如下形式:
(21)
此外, 根据a0(m,k)与a1(m,k)定义, 显然式(21)在j=1时也成立.
因此由(20)与(21),bj(m,k)与aj(m,k)满足相同的递推关系.而当j=0时, 由递推关系式(16)与b0(0,k)=1, 通过归纳法不难得到
b0(m,k)=(m+k)m,
即a0(m,k)=b0(m+k).
因此结论(15)得证.
显然引理1对任何m≥1, 给出了g(t)满足的一个m阶线性微分方程.现在借助(14), 我们已经准备完成定理1的证明.
定理的证明根据广义拉盖尔多项式的生成函数(11), 我们有
将上式两边对t求m阶导数并运用引理, 我们得到
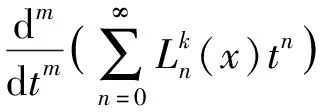
(22)
而
(23)
比较(22)与(23)两边tn的系数,我们就得到(12).从而定理成立.
2 结语
本文给出了关于广义拉盖尔多项式的一个新的递推关系,从而拓展了T.Kim、D.S.Kim、Hwang与Seo的工作,进一步深化了相关方向的研究.

