考虑碳排放权交易市场影响的日前电力市场两阶段出清模型

卢治霖，刘明波，尚 楠，陈 政，张 妍，黄国日

（1. 南方电网能源发展研究院有限责任公司,广东省广州市 510663；2. 华南理工大学电力学院,广东省广州市 510640）

0 引言

自中国提出“碳达峰、碳中和”的目标以来,碳排放权交易（carbon emissions trading,CET）已成为各方关注的焦点［1-2］。2020 年12 月中央经济工作会议提出要加快建设全国CET 市场,生态环境部随即印发系列文件推进市场建设［3］。2021 年7 月16 日,全国CET 市场正式启动上线交易［4］。与此同时,中国在电价改革、电力市场建设等方面取得了显著成效。2020 年,中国电力市场化交易规模达到3 170 TW·h,同比增长11.7%［5］,首批8 个电力现货试点结算试运行周期进一步拉长,第2 批6 个现货试点宣布启动［6］。目前,发电行业被率先纳入碳配额管理和全国CET 市场,将对中国现阶段的电力市场,尤其是对日前电力市场带来显著的影响,函待开展深入的研究。

目前,已有部分关于CET 市场运作对电力市场影响的研究。文献［7-8］基于均衡理论和系统动力学模型,模拟和分析了CET 市场与中长期电力市场间的相互影响。文献［9］提出的模型论证了碳排放强度相对较低的发电机组在市场中更有可能中标,该模型不仅可以利用用户侧各种资源的优势,而且可以反映出CET 市场机制对发电时间表的影响。文献［10］则以电力市场为基础,利用区块链技术提出了一种面向电力CET 的“泛双边”市场机制,以此来开展“集中申报撮合、分布式匹配出清”的CET。但是,由于CET 市场运作的时间尺度与日前电力市场不一致,上述文献的研究理论无法实时反映CET市场要素对日前电力市场出清情况的影响。因此,本文提出了考虑CET 市场和日前电力市场相互作用的市场框架。

研究CET 市场运作对日前电力市场影响的另一个重要方面是平衡不同目标主体之间的利益冲突,但文献［11-13］都仅聚焦于电力系统总运营成本在CET 市场运作下的变化。文献［11］采用寡头垄断的市场模型对电力市场进行建模,分析了不同碳排放配额分配方案对电力行业利润的影响,并提出适合政府自由分配的碳配额百分比。文献［12］基于经典的古诺均衡模型,针对不同类型机组分别进行建模,从而构建市场均衡的两层优化模型,来研究碳排放成本对电力市场均衡状态和市场成员策略性行为的影响。文献［13］通过建立综合考虑碳排放配额分配的安全约束机组组合模型,有效分析不同碳排放配额分配方案对机组组合结果、系统运行成本与利益格局变化所造成的影响,但其却忽略了不同主体之间的利益冲突,调度无法兼顾不同主体。因此,本文提出了考虑CET 市场运作影响的两阶段出清模型,在模型第1 阶段建立电力系统总运营成本最小和发电企业碳排放成本总和最小的多目标优化模型,实现了不同目标冲突的有效平衡。类似地,文献［14］建立了基于多目标概率最优潮流的区域电网低碳调度模型,平衡了发电成本、碳排放量与区域碳排放差异量3 个目标间的冲突。文献［15］对包含风电、梯级水电、传统机组以及碳捕集机组的风水火联合系统建立多目标优化调度模型。但文献［14-15］无法直接用于求解考虑CET 市场运作影响的电力市场边际价格。因此,本文在两阶段出清模型第2阶段建立以电力系统总运营成本最小为目标的追踪模型,使市场出清方案与第1 阶段计算结果一致,同时计算日前电力市场边际价格。

求解本文所提出的两阶段模型,关键是获得模型第1 阶段多目标优化问题的完整且分布均匀的Pareto 前沿。目前工程上的常用方法为加权和法［16-17］,该方法通过改变目标函数之间的权重来逐个寻找Pareto 最优解,但具有2 个明显缺点:1）该方法难以通过均匀分配目标函数间的权重来直接获得分布均匀的Pareto 前沿解［18］；2）传统加权和法无法通过减少步长在非凸区域找到Pareto 最优解［19］。采用规格化法平面约束法［20-21］求解多目标优化问题可以获得分布均匀的Pareto 前沿,但同样无法解决Pareto 前沿非凸区域的有效求解问题。因此,本文提出一种自适应加权和法［22］来计算多目标优化问题的Pareto 最优解。

综上,为分析CET 市场运作对日前电力市场出清情况的影响,本文首先搭建了考虑CET 市场和日前电力市场相互作用的市场框架,用以分析2 个市场的交互机理。然后,针对现有出清模型无法平衡不同目标冲突且控制碳排放效果不明显的缺点,提出了两阶段出清模型。第1 阶段,建立电力系统总运营成本最小和发电企业碳排放成本总和最小的多目标优化模型；第2 阶段,以最小化电力系统总运营成本为目标,建立满足第1 阶段Pareto 解约束的追踪模型。最后,针对传统加权和法难以获得多目标优化问题分布均匀的Pareto 前沿且无法在非凸区域找到Pareto 最优解的缺点,提出一种自适应加权和法来求解两阶段出清模型第1 阶段的多目标优化问题,获得该问题完整的Pareto 前沿。

1 市场框架与模型假设

1.1 市场框架

图1 为CET 市场与日前电力市场交互的市场框架。如图1 所示,燃煤、燃气机组同时参与CET市场和日前电力市场。燃煤、燃气机组在发电过程中会排放温室气体,政府会对其碳排放进行监控。此外,政府还负责在年初分配年度碳排放配额给各发电机组,并在年底核查这些机组的碳排放总量。

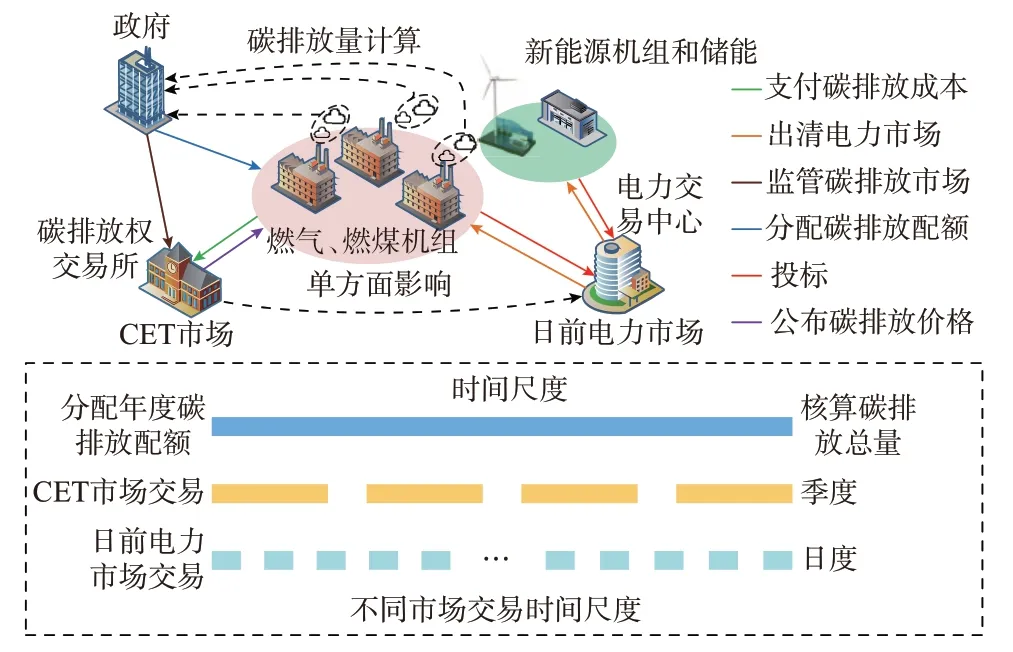
图1 考虑CET 市场和日前电力市场交互的市场框架Fig.1 Market framework considering interaction between CET market and day-ahead electricity market

CET 与日前电力市场之间的交互机理可总结为:在日前电力市场中,各发电机组每日都向电力交易中心提供投标信息,燃煤、燃气机组每季度在一级碳排放市场上交易碳排放配额,对于日前电力市场的特定运营日而言,碳价相对固定；在CET 市场中,燃煤、燃气机组可通过交易其剩余的碳排放配额来获得利润,当机组碳排放量超过其分配所得的免费配额时,该机组需要支付额外的碳排放成本,从而使得其发电成本攀升。因此,燃煤、燃气机组在日前电力市场投标前会根据政府分配的碳排放配额来评估其所需支付的碳排放成本。可以看到,CET 市场对日前电力市场具有单方面的影响。

1.2 模型假设

1.2.1 碳排放配额分配方法

目前,中国将各行业的碳排放配额分配下达时间尺度设定为年度。本文为研究CET 市场对日前电力市场的影响,将碳排放配额分配的时间尺度修改为一日。在分配各发电企业的碳排放配额前,首先要明确可供分配的碳排放总量。通常采用各发电企业在不参与CET 市场时所排放的温室气体总和作为基准值,然后在此基础上考虑对应的减排系数,即

式中:Q为日内全体发电企业可供分配的碳排放配额总量；Eb为各发电企业在不参与CET 市场时所排放的温室气体总和；α为减排系数。

目前,主要采用基于历史碳排放量和基于发电绩效标准这2 种方案来分配各发电企业的碳排放配额。

1）基于发电绩效分配碳排放配额

发电绩效G为发电企业在单位时间内每生产1 MW·h 电量所排放的温室气体数量［23］,即

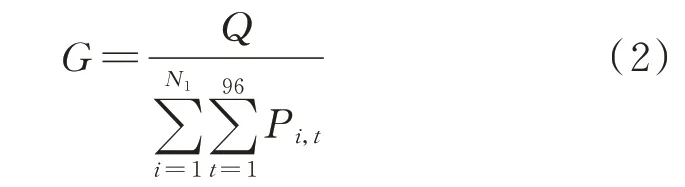
式中:Pi,t为常规机组i在t时段的出力；N1为常规机组总数。

因此,常规机组i按发电绩效分配获得的碳排放配额Eq,i为:

2）基于历史碳排放量分配碳排放配额

常规机组i获得的碳排放配额与其在不考虑CET 市场运作下的碳排放量占总量的比例成正比,即

1.2.2 燃气、燃煤机组分段报价

本文采用“发电侧报价报量、负荷侧报量不报价”的方式进行研究。当不考虑CET 市场运作时,常规机组的报价曲线为递增阶梯曲线,如图2所示。

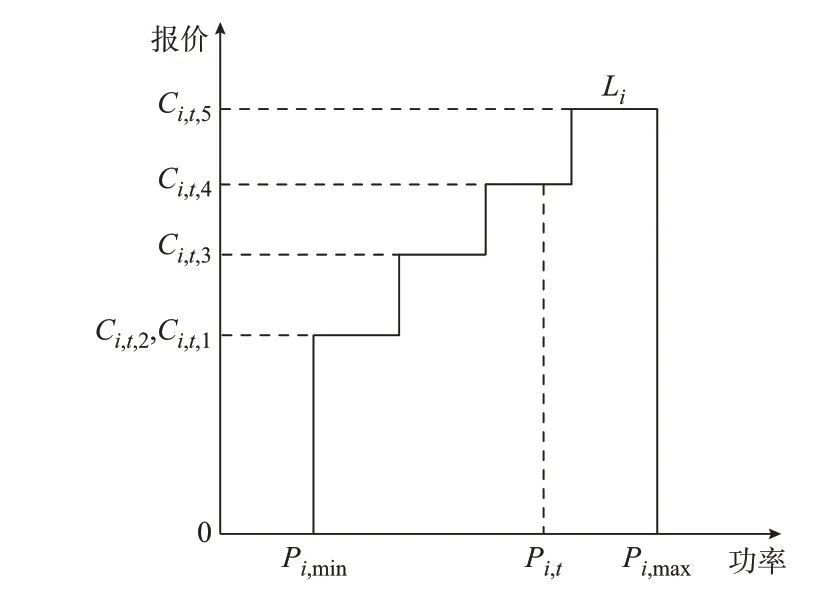
图2 常规机组的多段阶梯报价曲线Fig.2 Multi-segment step-bidding curve for conventional units

常规机组i在t时段的第k段报价Ci,t,k为:

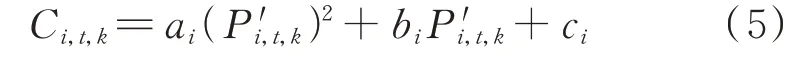
式中:ai、bi、ci为常规机组i的燃料成本系数；P′i,t,k为常规机组i在t时段的第k段报价对应的计算出力,如式（6）所示。

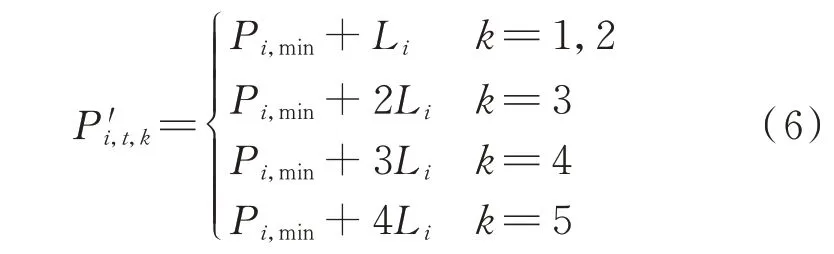
式中:Pi,min为常规机组i的最小出力；Li为常规机组i多段报价出力的长度,如式（7）所示。

式中:Pi,max为常规机组i的最大出力。

在CET 市场机制下,若常规机组i所产生的碳排放量超过其所分配的免费配额,则该机组需要支付对应的碳排放成本。可见,常规机组i的总发电成本将随着CET 市场的运作发生变化。因此,各常规机组会根据历史发电情况评估自身需要支付的碳排放成本,进而调整机组在日前电力市场中的报价情况。考虑CET 市场运作影响后,常规机组i在t时段的第k段报价为:

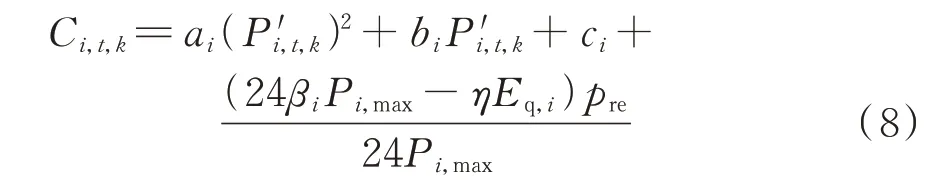
式中:pre为碳排放价格,本文设定为25 元/t；βi为常规机组i对应的碳排放强度系数；η为配额免费发放的比例。

2 两阶段出清模型

为了分析CET 市场对日前电力市场出清情况的影响,本文提出了考虑CET 市场影响的两阶段出清模型。该模型2 个阶段之间的关系如图3 所示。

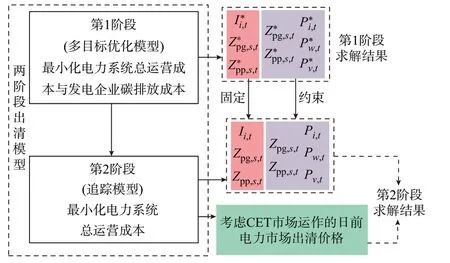
图3 模型2 个阶段之间的关系Fig.3 Relationship between two stages of model

图中,Ii,t为0-1 变量,表示常规机组i在t时段的启停状态,取值为1 表示处于开机状态,取值为0 表示处于停机状态；Zpg,s,t和Zpp,s,t分别为抽水蓄能机组s在t时段的发电和抽水状态,取值为1 表示处于对应状态,取值为0 表示不处于对应状态；Pw,t为第w台风电机组在t时段的出力；Pv,t为第v台光伏发电机组在t时段的出力；上标“*”表示对应变量在第1阶段根据多目标优化模型计算得到的结果。

在第1 阶段,本文对电力系统总运营成本和发电企业碳排放成本进行多目标优化,以确定燃煤、燃气机组的日内启停状态、抽水蓄能机组的日内抽水与发电状态以及各发电机组的各时段出力情况。模型第1 阶段得到的出清结果能够有效平衡2 个目标之间的利益冲突,但无法直接获得日前电力市场的边际价格。

在第2 阶段,本文利用第1 阶段求解获得的机组启停、发电与抽水状态来固定第2 阶段模型对应的状态变量。同时,根据第1 阶段各机组出力情况构建多目标优化模型结果约束,对第2 阶段机组出力进行限制。然后,根据模型第2 阶段计算获得的市场出清价格进一步分析CET 市场运作的影响。

2.1 第1 阶段：多目标优化模型

2.1.1 第1 阶段目标函数

1）最小化电力系统的总运营成本J1,其中运营成本包括购电费用、正负旋转备用费用、启停成本和空载成本,即

2）最小化各发电企业机组所需支付的碳排放成本总和J2,即

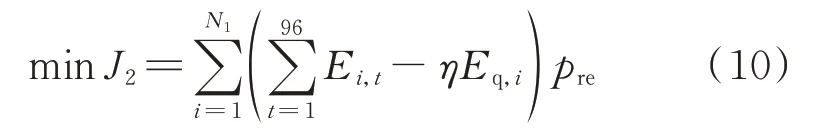
式中:Ei,t为常规机组i在t时段内的碳排放量,如式（11）所示。

2.1.2 第1 阶段约束条件

1）机组的开停机费用约束

开机费用约束可表示为:

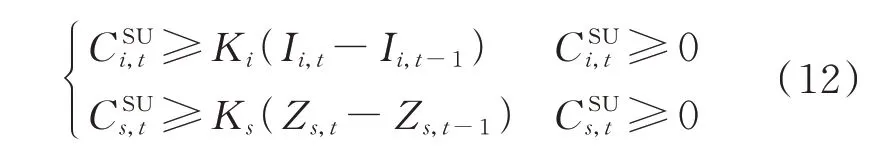
停机费用约束可表示为:

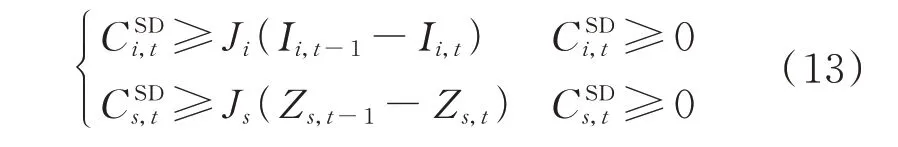
式中:Ki和Ji分别为常规机组i的单次开机和停机费用；Ks和Js分别为抽水蓄能机组s的单次开机和停机费用；Zs,t表示抽水蓄能机组s在t时段的启停状态,取值为1 表示启动,取值为0 表示停机。

2）系统功率平衡约束

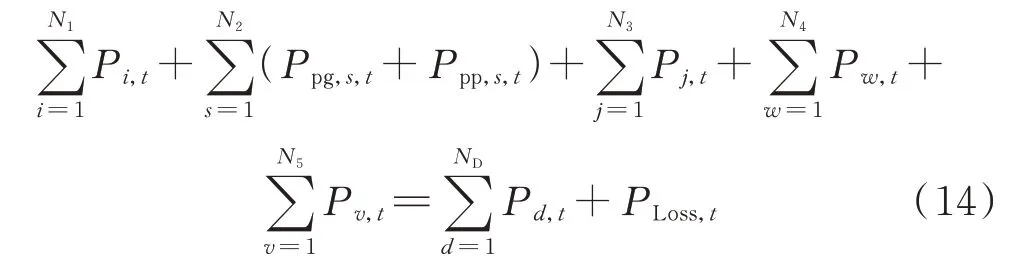
式中:Ppg,s,t和Ppp,s,t分别为抽水蓄能机组s在t时段的发电功率和抽水功率,发电功率为正,抽水功率为负；N3为系统与外电网联络线的数量；N4为风电机组数；N5为光伏发电机组数；ND为负荷节点数；Pj,t为第j条与外电网联络线在t时段对系统的注入功率；Pd,t为负荷节点d在t时段的负荷预测值；PLoss,t为t时段的系统网损。

3）常规机组出力约束

常规机组总出力的上下限约束可表示为:

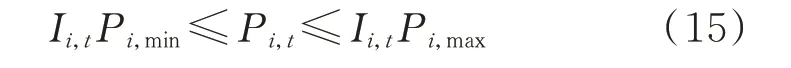
常规机组i在t时段各中标出力之和等于该机组t时段的总出力,如式（16）所示。

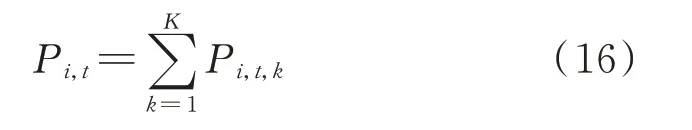
此外,常规机组每段出力还需满足段出力的上下限约束,如式（17）所示。

4）机组爬坡/滑坡约束

机组在开机的第1 个时段或停机的最后1 个时段的出力不超过机组的最小出力,则机组爬坡/滑坡约束可表示为:

5）机组最小开停机时间约束

机组最小开机时间约束可表示为:

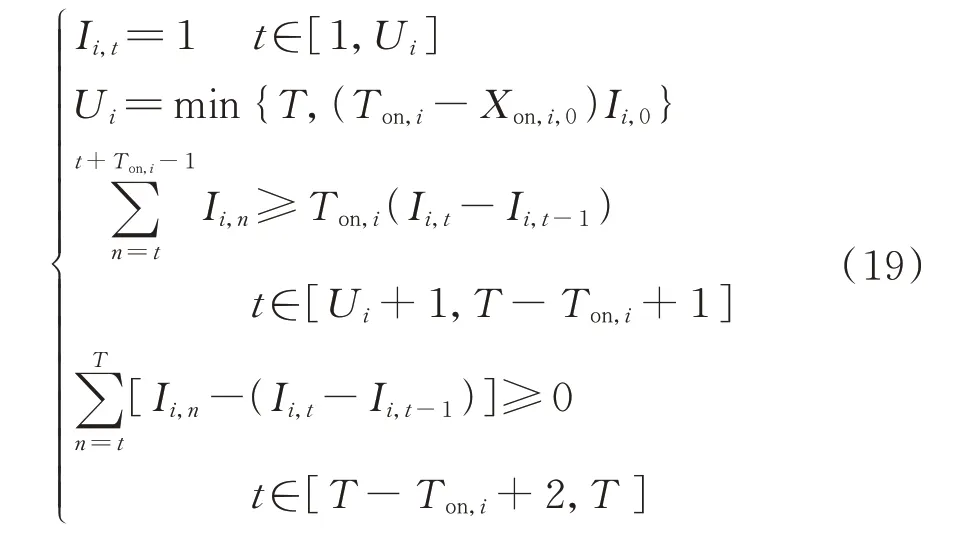
机组最小停机时间约束可表示为:

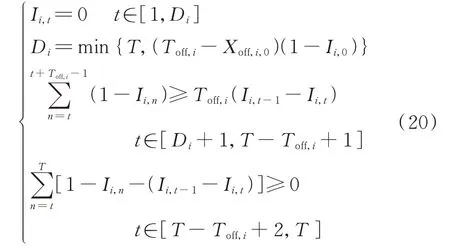
式中:Ui和Di分别为常规机组i从调度周期开始后必须开机、停机的时段,是由上个调度周期结束时机组的状态决定的；T为总时段数；Ton,i和Toff,i分别为常规机组i的最小开机、停机时间；Xon,i,0和Xoff,i,0分别为常规机组i在调度周期开始时已经连续开机、停机的时间；Ii,0为常规机组i的初始启停状态。

6）抽水蓄能机组的运行约束

抽水蓄能机组出力的上下限约束可表示为:

式中:Ppg,s,max和Ppp,s,max分别为抽水蓄能机组s的最大发电功率和最大抽水功率。

运行工况互补约束（同一时段抽水蓄能机组不可能同时处于抽水和发电工况）可表示为:

实际运行中还需要满足日电量平衡约束,即

式中:ξ为抽水蓄能机组的转换效率,通常取75%。

7）旋转备用约束

通过预留足够的系统旋转备用容量以应对负荷预测误差带来的影响。利用正旋转备用容量补偿因低估系统负荷带来的影响,利用负旋转备用容量补偿因高估系统负荷带来的影响。

常规机组旋转备用约束可表示为:

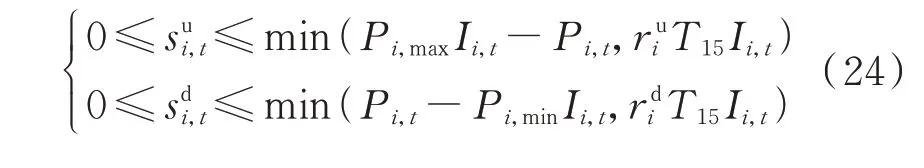
抽水蓄能机组旋转备用约束可表示为:

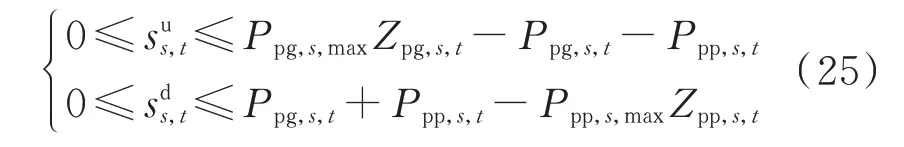
累加所有机组的旋转备用得到系统的旋转备用需求约束如下:

式中:Lu和Ld分别为负荷预测偏差对系统正、负旋转备用容量的需求系数。

8）燃气-蒸汽联合循环机组

在模型中考虑对一套燃气-蒸汽联合循环机组的2 台机组分别进行调度。假设Ii,t和Ij,t分别表示一套燃气-蒸汽联合循环机组的大容量机组和小容量机组的启停状态,控制其启停状态一致,即

9）新能源机组出力的上下限约束

当电力系统某一时刻下,传统发电机组备用容量不足或靠近新能源发电系统并网处的线路传输容量的限制,弃风或弃光是不可避免的。因此,新能源出力约束可表示为:

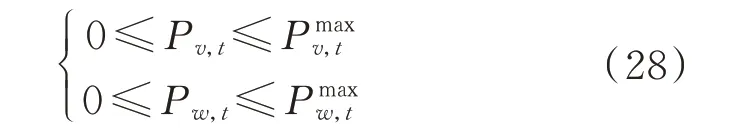
10）网络传输约束

根据直流潮流模型,线路传输功率约束如下:

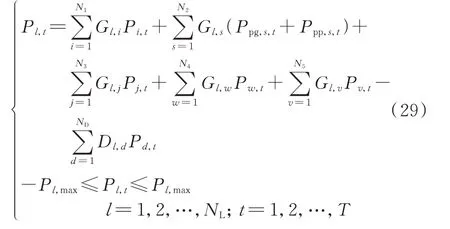
式中:Pl,t为t时段输电线路l的传输功率；NL为输电线路条数；Gl,i、Gl,s、Gl,j、Gl,w、Gl,v和Dl,d分别为输电线路l与常规机组i、抽水蓄能机组s、外电网联络线j、风电机组w、光伏发电机组v和负荷d之间的有功功率传输因子；Pl,max为输电线路l的最大传输容量。

为了便于研究讨论,可将上述优化模型改写成以下紧凑形式:

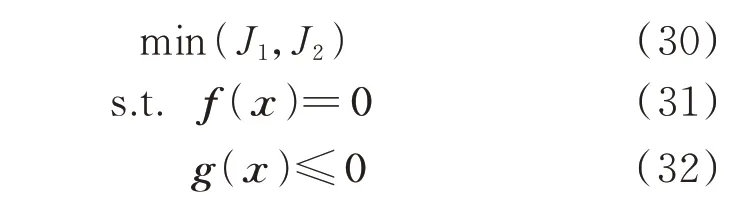
式中:f(x)=0 表示模型中的等式约束,包括约束式（14）、式（16）、式（23）和式（27）；g(x)≤0 表示模型中的不等式约束,包括约束式（12）、式（13）、式（15）、式（17）至式（22）、式（24）、式（25）、式（28）、式（29）。

2.2 第2 阶段：追踪模型

日前电力市场出清本质上是一个基于安全约束的机组组合问题［24］,因此,可通过功率平衡约束的拉格朗日乘子等信息得到日前电力市场边际价格的解析表达式。在第1 阶段,本文通过多目标优化模型较好地平衡了不同目标之间的利益冲突,但无法直接获得市场边际价格信息。在第2 阶段,本文提出了基于传统经济调度模型的追踪模型,利用从第1 阶段获得的求解结果来确定燃煤、燃气机组的启停状态和抽水蓄能机组的发电与抽水状态,并进一步约束上述机组的出力。

2.2.1 第2 阶段目标函数第2 阶段的目标为在常规机组启停状态和抽水蓄能机组发电与抽水状态确定的情况下,将系统的总运行成本J降到最低,如式（33）所示。

2.2.2 第2 阶段约束条件

第2 阶段约束条件除了第1 阶段模型中的约束式（14）至式（18）、式（21）、式（23）至式（26）、式（28）、式（29）以外,还需要加入如式（34）至式（37）所示的多目标优化模型结果约束。

式中:ε为松弛误差,本文设定为0.000 000 1。

另外,日前市场出清模型采用节点电价定价机制,形成每15 min 的节点电价,其计算公式为:

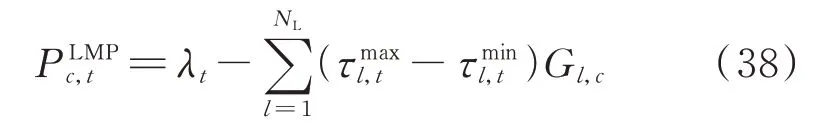
由式（38）可知,当忽略网络传输约束时,整个系统的节点电价相同；当考虑网络传输约束且系统中出现阻塞时,阻塞线路两端的节点电价不同。

3 采用自适应加权和法求解多目标优化模型的Pareto 最优解

本章具体介绍第2 章提出的两阶段出清模型的求解算法。显然,两阶段模型的第2 阶段是典型的线性规划问题,可通过调用Gurobi 求解器直接进行求解。而模型的第1 阶段是多目标混合整数线性规划问题,目前常用的方法为加权和法,但该方法难以通过均匀分配目标函数间的权重来直接获得分布均匀的Pareto 前沿解,也无法通过减少步长在非凸区域找到Pareto 最优解。

因此,针对两阶段模型第1 阶段的多目标优化问题,本文提出一种自适应加权和法来计算模型的Pareto 最优解。采用自适应加权和法计算时,目标函数间的权重分配方案无须提前确定,而是根据优化问题Pareto 前沿的性质进行变化。首先,采用较大的权重步长Δλ计算获得少量Pareto 前沿解,并识别需要进一步细化计算的区域。其次,通过在目标区域中施加不等式约束,将特定区域指定为子多目标优化问题的可行区域。然后,在上述区域采用典型加权和法对子多目标优化问题进行求解。当计算获得的Pareto 前沿的所有区域都达到预定精度时,算法终止。采用自适应加权和法求取多目标优化模型的Pareto 最优解的主要步骤如下。

步骤1:根据式（31）、式（32）构造最小化电力系统的总运营成本J1的单目标优化问题,通过计算求得J1的最小值Jmin1,此时可对应求得各发电企业机组所需支付的碳排放成本总和为Jmax2。步骤2:根据式（31）、式（32）构造最小化各发电企业机组所需支付的碳排放成本总和J2的单目标优化问题,通过计算求得J2的最小值Jmin2,此时可对应求得电力系统的总运营成本Jmax1。

步骤3:通过步骤1 和2 计算得到的Jmin1、Jmax1、Jmin2、Jmax2对目标函数式（30）进行规格化处理,即

步骤4:采用传统的加权和法以较小的分段数ninitial对规格化后的多目标模型进行求解,目标函数的权重因子λ的统一步长由分段数ninitial决定,即

由于步骤4 中权重因子的步长较大,该步骤计算获得的解数量较少。

步骤5:计算步骤4 获得的所有相邻解的欧氏距离,根据设定的精度μ删除几乎重叠的解,即当相邻解间的欧氏距离小于μ时,保留其中一个解,删除其余解。

步骤6:将步骤5 筛选出来的解进行整理,其中每2 个相邻解组成一个区域,然后确定各区域中需要细化计算的次数。区域a中2 个端点的欧氏距离越长,则区域a需要细化计算的次数越多。各区域的细化程度根据区域两端点欧氏距离的相对长度进行确定,如式（41）所示。

式中:na为区域a需要细化计算的次数；la为区域a两端点的欧氏距离；lavg为所有区域两端点欧氏距离的平均长度；C为提前设定常数。

步骤7:若na≤1,则区域a无须进一步细化计算；若na＞1,则继续执行步骤8。

图4 基于δJ确定偏移距离Fig.4 Determination of offset distances based on δJ

为了得到平行于坐标轴的偏移距离δ1和δ2,需要进一步计算图4（b）中的角度θ,如式（42）所示。

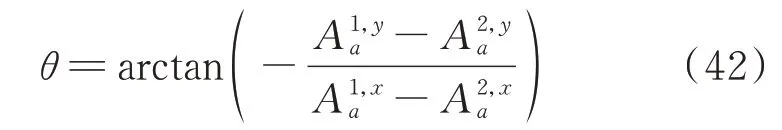
进一步地,可根据偏移距离δJ与角度θ分别计算偏移距离δ1和δ2,如式（43）所示。

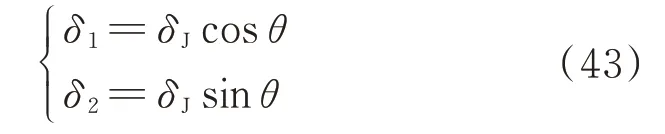
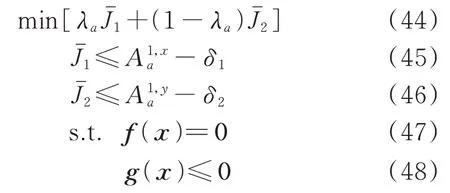
式中:λa为区域a可行域的权重因子,其统一步长Δλa根据步骤6 计算获得的细化计算次数na决定,如式（49）所示。

删除细化计算过程中无法收敛获得最优解的区域,因为在这种情况下被删除区域是非凸且不包含Pareto 最优解的。

步骤10:计算所有相邻解之间的拉格朗日距离,删除几乎重叠的解。若所有区域两端点的拉格朗日距离均小于μ,则结束优化过程。如果存在两端点拉格朗日距离大于μ的区域,则跳转至步骤6进行迭代计算。

4 算例分析

4.1 测试系统概况

本文采用中国某省级实际2278 节点系统进行仿真,以验证所提出模型的有效性。该系统包括1 462 条线路,232 台发电机组。其中,核电机组11 台,容量为11 550 MW,其出力全天恒定,不参与优化。参与优化的机组为221 台,包括抽水蓄能机组14 台、光伏发电机组10 台、风电机组10 台、燃煤机组116 台、燃气机组63 台、水电机组8 台。总负荷预测曲线如图5 所示,最大功率为118 240 MW,最小功率为79 399 MW,同时,设定PLoss,t为t时段系统总负荷的0.75%。

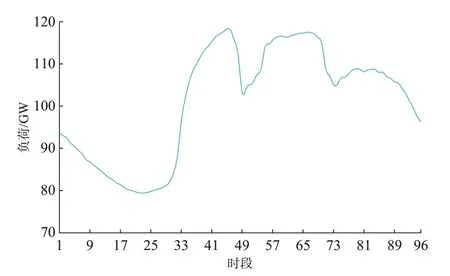
图5 总负荷预测曲线Fig.5 Prediction curve of total load

4.2 采用自适应加权和法求解多目标优化模型

首先,基于历史碳排放量分配各常规机组的碳排放配额。然后,分别采用加权和法与自适应加权和法求解第1 阶段的多目标优化模型。图6（a）为采用加权和法求解获得的Pareto 最优解,图6（b）至（f）则为采用自适应加权和法获得的Pareto 最优解。图6（a）中共有16 个Pareto 最优解,但是绝大部分解都集中在左上方与右下方区域,无法有效描绘出多目标优化问题完整的Pareto 前沿。相反地,根据图6（b）至（f）,采用自适应加权和法求解第1 阶段的多目标优化问题时,经过5 次迭代后实现收敛,得到分布均匀的Pareto 最优解,同时在非凸区域实现Pareto 最优解求取。如图6（f）中红点所示,当= 0.000 1、=0.151 2 时,电力系统总运营成本接近最小值且发电企业需要支付的碳排放成本总和较小,因此,本文选择(,)=(0.000 1,0.151 2)作为两阶段出清模型第1 阶段多目标优化问题的折中最优解。

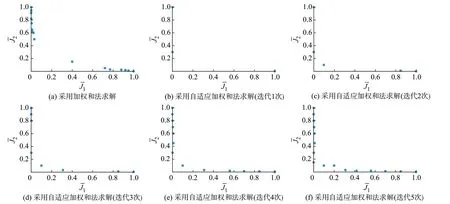
图6 采用加权和法与自适应加权和法求解第1 阶段的Pareto 前沿Fig.6 Solution of Pareto front at the first stage using weighted-sum method and adaptive weighted-sum method

传统出清模型［24］仅以电力系统总运行成本为单独目标进行优化,这将大大减少CET 机制对碳排放总量的控制。为突出所提出的两阶段模型的优越性,本文对比了两阶段出清模型与传统出清模型在CET 市场运作影响下的出清结果,如表1 所示。

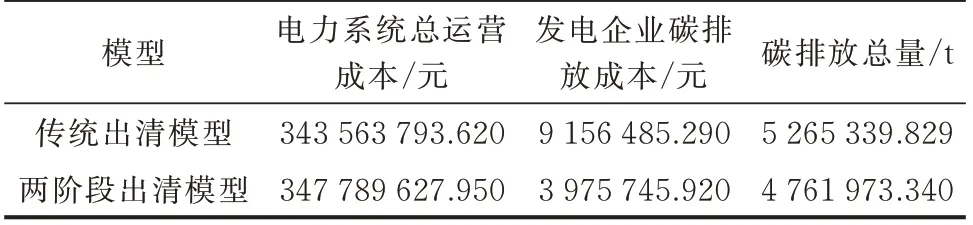
表1 2 种出清模型结果对比Table 1 Comparison of results between two clearing models

根据表1 可得,两阶段出清模型计算获得的电力系统总运营成本仅比传统出清模型中的费用高1.23%,但其发电企业所需支付的总碳排放成本减少了56.58%,碳排放总量减少了9.56%。可见,两阶段出清模型尽管无法降低电力系统总运营成本,但可极大程度地降低常规机组在CET 市场中所需支付的碳排放成本,较好地平衡不同目标之间的利益冲突,并有效降低系统碳排放总量。

4.3 考虑CET 市场影响的日前电力市场出清价格计算

本文采用两阶段出清模型计算考虑CET 市场运作影响的日前电力市场出清价格,并将出清价格与不考虑CET 市场运作得到的计算结果进行对比,如图7 所示。可以看到,考虑CET 市场运作后,电力市场出清价格发生变化,出清价格在日内全部时段比未考虑CET 市场运作时明显上升,最高幅度为26.99%,价格的日内变化趋势与以往相同。

图7 日前电力市场出清价格对比Fig.7 Comparison of clearing prices of day-ahead electricity market

图8 给出了日前电力市场加权平均出清价格伴随减排系数变化的情况。可以看到,随着减排系数的不断增加,日前电力市场加权平均出清价格也逐渐升高。当减排系数在35%以内时,电力市场出清价格涨幅速度较为缓慢,而当减排系数大于35%时,日前电力市场出清价格迅速上涨。这是由于当减排系数增加到一定比例时,燃煤、燃气机组在CET 市场中均无法获得充足的配额,需要支付昂贵的碳排放成本,从而抬高常规机组在日前电力市场的报价,进而导致电力市场出清价格大幅度上涨。

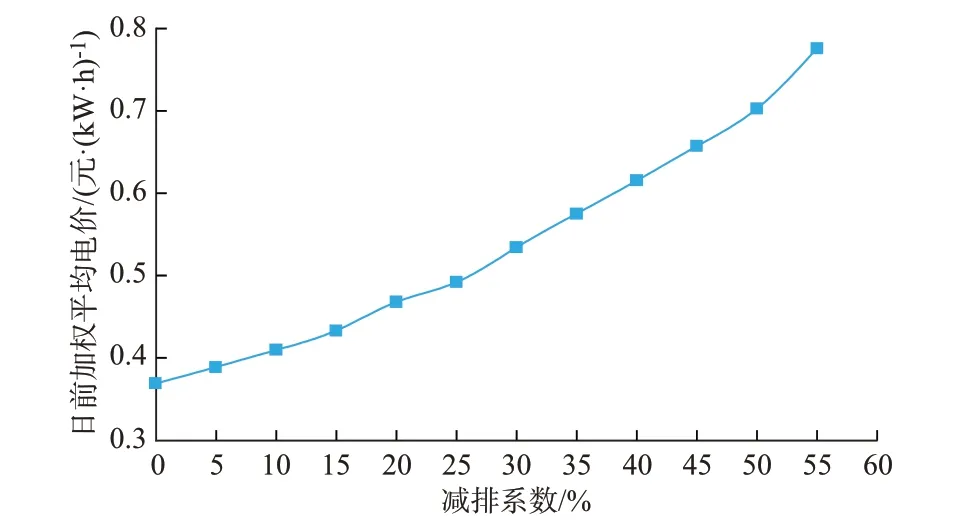
图8 日前加权平均电价随减排系数变化的曲线Fig.8 Curve of day-ahead weighted average electricity price with change of emission reduction factor

日前加权平均电价与碳排放价格之间的关系如图9 所示。可以看到,随着碳排放价格不断增加,燃煤、燃气机组在CET 市场中需要支付的碳排放成本随之上升。为确保机组在日前电力市场中获得足够的收益,常规机组将抬高其市场中的报价,从而拉升市场价格。当碳排放价格超过45 元/t 时,电力市场出清价格将迅速上升。

图9 日前加权平均电价随碳价变化的曲线Fig.9 Curve of day-ahead weighted average electricity price with change of carbon price

4.4 不同碳排放配额分配方案的市场出清情况对比

图10 对比了燃煤机组在不同碳排放配额分配方案下的总体出力情况。可以看到,由于燃煤机组的碳排放强度系数较高,为减少发电企业在CET 市场中所需支付的碳排放成本总和,燃煤机组的出力在负荷低谷时段将会被较大程度地削减。进一步地,由于燃煤机组的发电绩效较低,若基于发电绩效方案分配各机组碳排放配额,燃煤机组的出力将会进一步被削减,削减程度最高可达38.4%。

图10 燃煤机组出力对比Fig.10 Comparison of outputs of coal-fired units

图11 对比了燃气机组在不同碳排放配额分配方案下的总体出力情况。可以看到,尽管燃气机组的发电边际成本较高,但该类机组的碳排放强度系数较低,发电产生的碳排放量较少,无须在CET 市场中支付昂贵的碳排放成本。在燃煤机组出力被大幅度削减的情况下,为满足功率平衡需求,燃气机组出力将上升。当基于发电绩效方案来分配机组碳排放配额时,燃气机组出力上升幅度最高可达41.50%。

图11 燃气机组出力对比Fig.11 Comparison of outputs of gas-fired units

新能源机组出力的对比情况如图12 和图13 所示。由于该类机组在发电过程中不产生碳排放,其运行成本较低,且系统调峰能力充足,新能源机组未受到CET 市场运作影响,其出力被系统全部消纳。

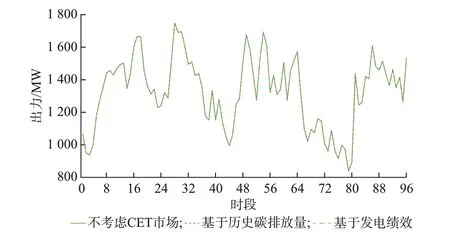
图12 风电机组总体出力对比Fig.12 Comparison of total outputs of wind turbines

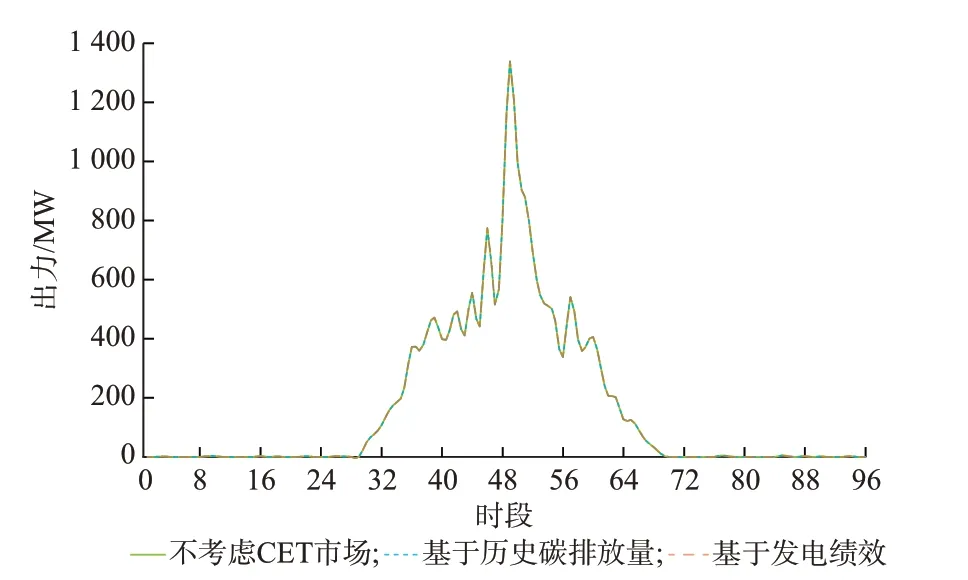
图13 光伏机组总体出力对比Fig.13 Comparison of total outputs of photovoltaic units

图14 对比了抽水蓄能机组在不同碳排放配额分配方案下的总体出力情况。可以看到,由于CET市场的运作改变了燃煤、燃气机组在日前电力市场中的中标情况,从而一定程度上减少了系统的峰谷差,进而压缩了抽水蓄能机组的运行空间。因此,CET 市场运作可减少抽水蓄能机组的策略性充放电行为,该现象在基于发电绩效来分配机组碳排放配额时更为明显。

图14 抽水蓄能机组出力对比Fig.14 Comparison of outputs of pumped storage units

图15 对比了两阶段出清模型在不同碳排放配额分配方案下得到的日前电力市场出清价格。可以看到,基于发电绩效分配常规机组的碳排放配额时,发电成本较低的燃煤机组由于无法获得充足的配额,在CET 市场中需要支付昂贵的碳排放成本。因此,燃煤机组将相应的碳排放成本添加至其在日前电力市场的报价中。这导致所有常规机组的市场报价都处于较高的水平。相比基于历史碳排放量的方案,两阶段出清模型在采用基于发电绩效分配机组的碳排放配额时,计算得到的日前电力市场出清价格上升幅度更高,在负荷高峰时段尤为明显,最高可达26.79%。

图15 不同碳排放配额分配方案下的出清价格对比Fig.15 Comparison of clearing prices with different carbon emission quota allocation schemes

5 结语

本文提出了两阶段出清模型来分析CET 运作对日前电力市场的影响。首先,基于CET 市场和日前电力市场相互作用的市场框架,分析2 个市场的交互机理。然后,针对现有出清模型无法平衡不同目标冲突且控排效果不明显的缺点,提出了考虑CET 市场影响的日前电力市场两阶段出清模型。针对传统加权和法难以获得多目标优化问题分布均匀的Pareto 前沿且无法在非凸区域找到Pareto 最优解的缺点,提出一种自适应加权和法来求解两阶段出清模型第1 阶段的多目标优化问题,获得该问题完整的Pareto 前沿。最后,对一个实际的省级系统进行分析,结果表明CET 市场运作会抬高日前电力市场出清价格。基于发电绩效方案分配机组碳排放配额时,燃煤机组出力削减幅度更大,日前电力市场出清价格提升幅度更高。

本文对CET 市场启动初期如何兼顾减排效果与社会福利具有一定参考意义,但将发电企业在日前电力市场中的报价设定为固定参数,忽略了发电企业在市场中的博弈竞价行为。后续研究将进一步考虑发电企业在日前电力市场的博弈行为,分析CET 市场运作对不同发电企业主体的竞价策略影响。