航天高压氦气节流效应分析

(北京航天发射技术研究所，北京 100076)

引言

在我国现役低温运载火箭中，高压氦气主要应用在储箱增压、气瓶充气和发动机吹除等方面。在航天领域，氦气最高储存压力可达45 MPa，使用时一般通过减压阀或节流阀将压力降低至需求压力，气体经过节流后温度可能会发生变化。根据工程热力学定义可知，把节流后温度不变的气流温度叫做转回温度，在T-p图上把不同压力下的转回温度连起来可得到一条转回曲线，转回曲线与温度轴上方的交点成为最大转回温度，气体温度高于最大转回温度时产生节流热效应。氦气的最高转回温度约为47 K，航天常用的氦气温度范围(223.15～373.15 K)均高于该温度，高压氦气经减压节流后会出现温升效应[1]，如果减压节流产生的温升超过航天设备的允许温度范围，则可能影响设备的正常运行，甚至会对火箭发射和飞行任务造成影响，因此，有必要针对高压氦气的节流效应开展定量研究。

孙庆国等[2]根据等焓曲线查图法研究了高压氦气的节流效应，但等焓曲线法在实际应用和仿真计算中存在诸多不便；国内有学者根据经典气体状态方程推导了焦耳-汤姆逊系数计算公式，并根据公式计算了天然气、氢气、氮气、空气和二氧化碳的焦耳-汤姆逊系数，获得了较高的计算精度[3-7],也有学者采用CFD对空气、天然气和液压油等介质的节流效应进行了数值模拟研究[8-15]；谢太浩[16]通过对实验数据进行拟合，得到了计算低压氧气焦耳-汤姆逊系数的经验公式。到目前为止，尚未发现对高压氦气焦耳-汤姆逊效应数值计算方面的研究。

本研究针对航天领域用高压氦气，分别通过经典气体状态方程和经验公式法求解高压氦气焦耳-汤姆逊系数，并将计算与实验结果进行对比，获得求解高压氦气焦耳-汤姆逊系数的最佳方法，并根据得到的氦气焦耳-汤姆逊系数求解方法计算氦气的节流温升，用以指导实际工程应用。

1 焦耳-汤姆逊(JT)效应

1.1 焦耳-汤姆逊系数

高压流体经节流膨胀后，由于压力变化而引起温度的变化，该现象被称为节流效应或者焦耳-汤姆逊效应。节流膨胀过程无对外做功，节流过程时间较短，可认为是绝热膨胀，同时节流前后宏观动能和位能变化不大，因此，节流膨胀过程可近似看作等焓过程。

实际气体在等焓节流过程中温度随压力变化的速率称为焦耳-汤姆逊系数，实际气体的焓为温度和压力的函数，其表达式见式(1)，根据等焓条件求得焦耳-汤姆逊系数的表达式如式(2)所示：

(1)

(2)

式中,h—— 气体的焓，J

μJT—— 焦耳-汤姆逊系数，K/MPa

p—— 压力，MPa

T—— 温度，K

ν—— 摩尔体积，cm3/mol

Cp—— 实际气体的摩尔比定压热容，J/(mol·K)

当μJT=0时，气体节流前后温度不发生变化；当μJT<0时，气体节流后温度升高，称为焦耳-汤姆逊热效应；当μJT>0时，气体节流后温度降低，称为焦耳-汤姆逊热冷效应。

焦耳-汤姆逊系数μJT可由实际气体状态方程求出，也可采用经验公式进行求解。本研究选用的实际气体状态方程为经典范德瓦尔斯状态方程(简称VDW方程)和雷德利希-邝式状态方程(简称R-K方程)。

1.2 基于VDW方程求解μJT

1873年，范德瓦尔斯对理想气体状态方程进行了修订，提出了VDW方程，表达式如下[17]：

(3)

(4)

(5)

式中，R —— 气体常数，8.314 J/(mol·K)

a—— 范德瓦尔斯常数，cm6/mol2

b—— 范德瓦尔斯常数，cm3/mol

Tc—— 临界温度，K

pc—— 临界压力，MPa

对于氦气，Tc为5.19 K，pc为0.227 MPa。p，ν，T三者之间存在如下关系：

(6)

根据式(6)，焦耳-汤姆逊系数可转化如下：

(7)

由VDW方程可得出：

(8)

(9)

将式(8)和式(9)带入式(7)，求得焦耳-汤姆逊系数μJT如下：

(10)

根据式(10)可知，已知压力p和温度T，只需求解出实际气体的摩尔比定压热容Cp和摩尔体积ν即可求得焦耳-汤姆逊系数μJT。

将VDW方程转化为标准形式的关于摩尔体积ν的一元三次方程如下：

pν3-(pb+RT)ν2+aν-ab=0

(11)

对式(11)，应用盛金公式[18]可求解出实际气体的摩尔体积ν。

实际气体的摩尔比定压热容Cp既是温度的函数，又是压力的函数，根据剩余焓和VDW状态方程，可推导出氦气的摩尔比定压热容Cp计算公式，见式(12)，具体推导过程参见文献[3]：

(12)

根据式(10)～式(12)可知，实际气体的摩尔比定压热容Cp和摩尔体积ν为关于压力p和温度T的函数，因此已知p和T，即可由VDW方程求得实际气体的焦耳-汤姆逊系数μJT。

1.3 基于R-K方程求解μJT

1949年，雷德利希(Redlich)和邝(Kwong)在范德瓦尔斯状态方程的基础上进行了修订，提出了雷德利希-邝式状态方程，简称R-K方程，表达式如下[17]：

(13)

(14)

(15)

式(13)～式(15)中:

ar—— R-K方程常数，K0.5·cm6/mol2

br—— R-K方程常数，cm3/mol

由R-K方程可得出：

(16)

(17)

将式(15)和式(16)带入式(6)，求得焦耳-汤姆逊系数μJT与压力p和温度T的关系如下：

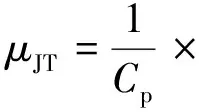
(18)

根据式(18)可知，已知压力p和温度T，只需求解出实际气体的摩尔比定压热容Cp和摩尔体积ν即可求得μJT。

将R-K方程转化为标准形式的关于摩尔体积ν的一元三次方程如下：

arbr=0

(19)

对式(19)，同样应用盛金公式可求解出实际气体的摩尔体积ν。

同理，根据剩余焓和R-K状态方程，可推导出氦气的摩尔比定压热容Cp计算公式，见式(12)，具体推导过程参见文献[3]：

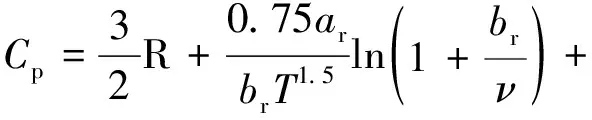
(20)

联立式(18)～式(20)，同样已知压力p和温度T，即可由R-K方程求得实际气体的焦耳-汤姆逊系数μJT。

1.4 经典状态方程计算误差分析

根据目前航天领域高压氦气的使用温度范围(223.15～373.15 K)和压力范围(0.1～45 MPa)，选取典型工况分别代入式(10)和式(18)计算焦耳-汤姆逊系数，并与实验得到的焦耳-汤姆逊系数进行对比，如表1所示，表中所列的氦气焦耳-汤姆逊系数的实验数据由物性数据库查得。根据表1可知，经典VDW方程和R-K状态方程计算结果和实际实验结果均为负值，说明航天领域高压氦气在使用温度和压力范围内节流产生热效应。在进行高压阀门和气动系统设计时应考虑节流升温对供气元件、设备和系统的影响。

当氦气温度高于最高转回温度时，气体分子之间的作用力以排斥力为主导[19-20]。节流后，气体体积膨胀，分子间距离增大，分子内部势能减小，由于系统绝热，总能量维持不变，分子总势能的减小导致总动能的增加，即分子运动变快，气体温度的升高，表现为节流热效应。

同时，表1显示VDW状态方程和R-K状态方程计算的氦气焦耳-汤姆逊系数均与实验数据偏差较大，其中VDW状态方程计算结果平均相对误差约75%；R-K状态方程计算结果平均相对误差约27%。

根据上述分析计算可知，经典气体状态方程VDW方程和R-K方程计算氦气的焦耳-汤姆逊系数误差较大，难以应用于实际工程，下面通过经验公式法对氦气的焦耳-汤姆逊系数进行求解。

1.5 推导经验公式求解μJT

根据航天领域高压氦气的使用温度范围和压力范围，在物性数据库中查得典型氦气焦耳-汤姆逊系数的实验结果，并绘制焦耳-汤姆逊系数关于温度和压力的曲线，如图1所示。

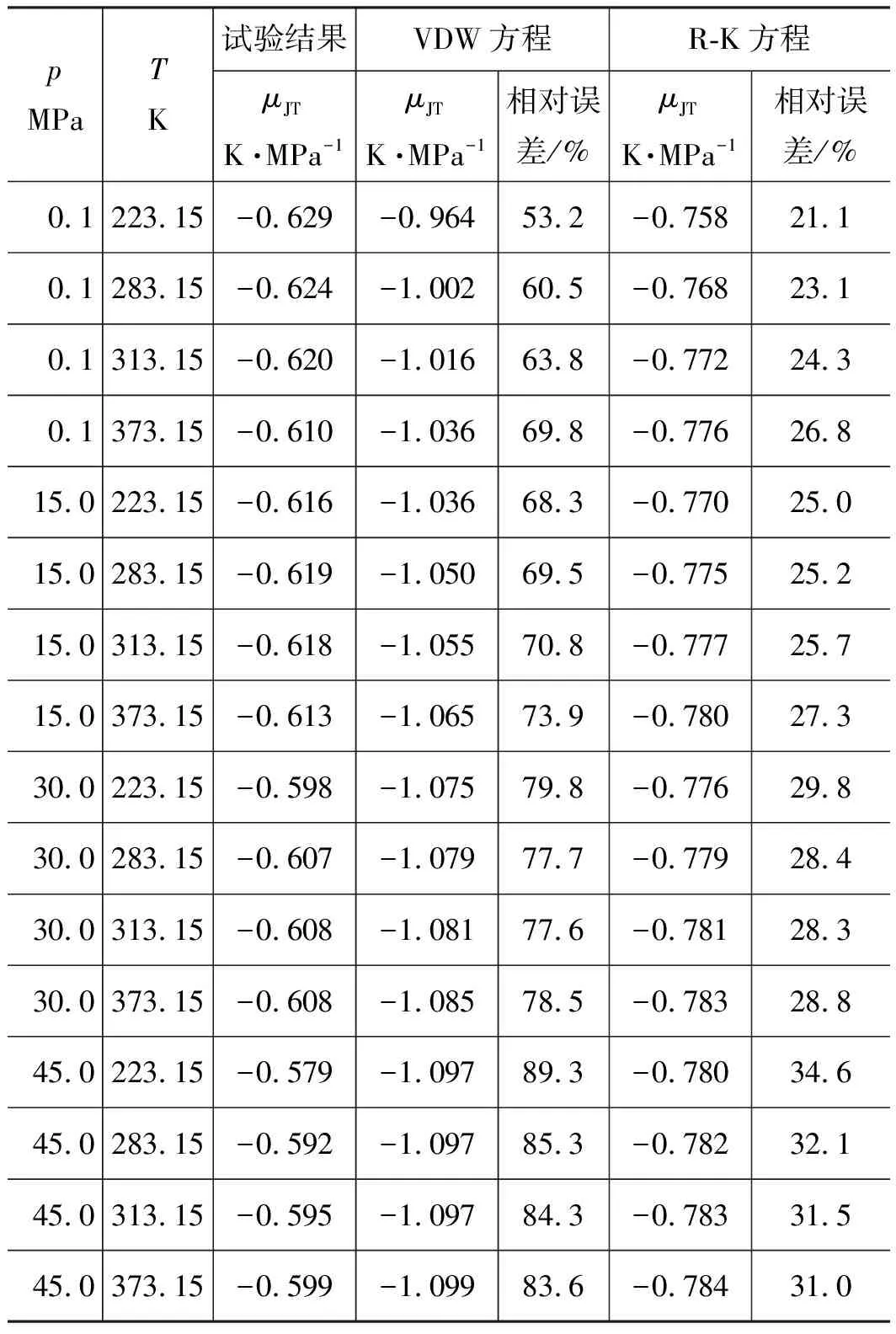
表1 试验结果和经典气体状态方程计算结果对比Tab.1 Comparison of experimental data with results of classic gas equation

图1 氦气焦耳-汤姆逊系数实验结果Fig.1 Experimental results of Joule-Thomson coefficient of Hilium

根据图1可知，氦气的焦耳-汤姆逊系数与压力近似成二次方关系，受温度影响较小，因此，工程计算中可忽略温度影响，将氦气的焦耳-汤姆逊系数对压力进行二次回归，得出经验公式如下：

μJT=9×10-6p2+4×10-4p-0.6264

(21)

为验证二次回归方程适用性，在航天领域高压氦气的使用温度和压力范围内选取典型工况代入式(21)计算焦耳-汤姆逊系数，并与实验得到的焦耳-汤姆逊系数进行对比，如表2所示。

由表2可知，采用经验公式计算的氦气焦耳-汤姆逊系数均与实验数据偏差较小，平均相对误差约0.8%，最大相对误差为2.67%。由于篇幅限制，只列举了典型温度和压力工况下的焦耳-汤姆逊系数经验公式计算结果，针对航天领域氦气压力和温度范围内多种使用工况进行了计算，经验公式计算结果和实验结果最大相对误差在3%以内。由此可知，经验公式法相比气体状态方程法计算量较小，且计算精度较高，可应用于工程实际。

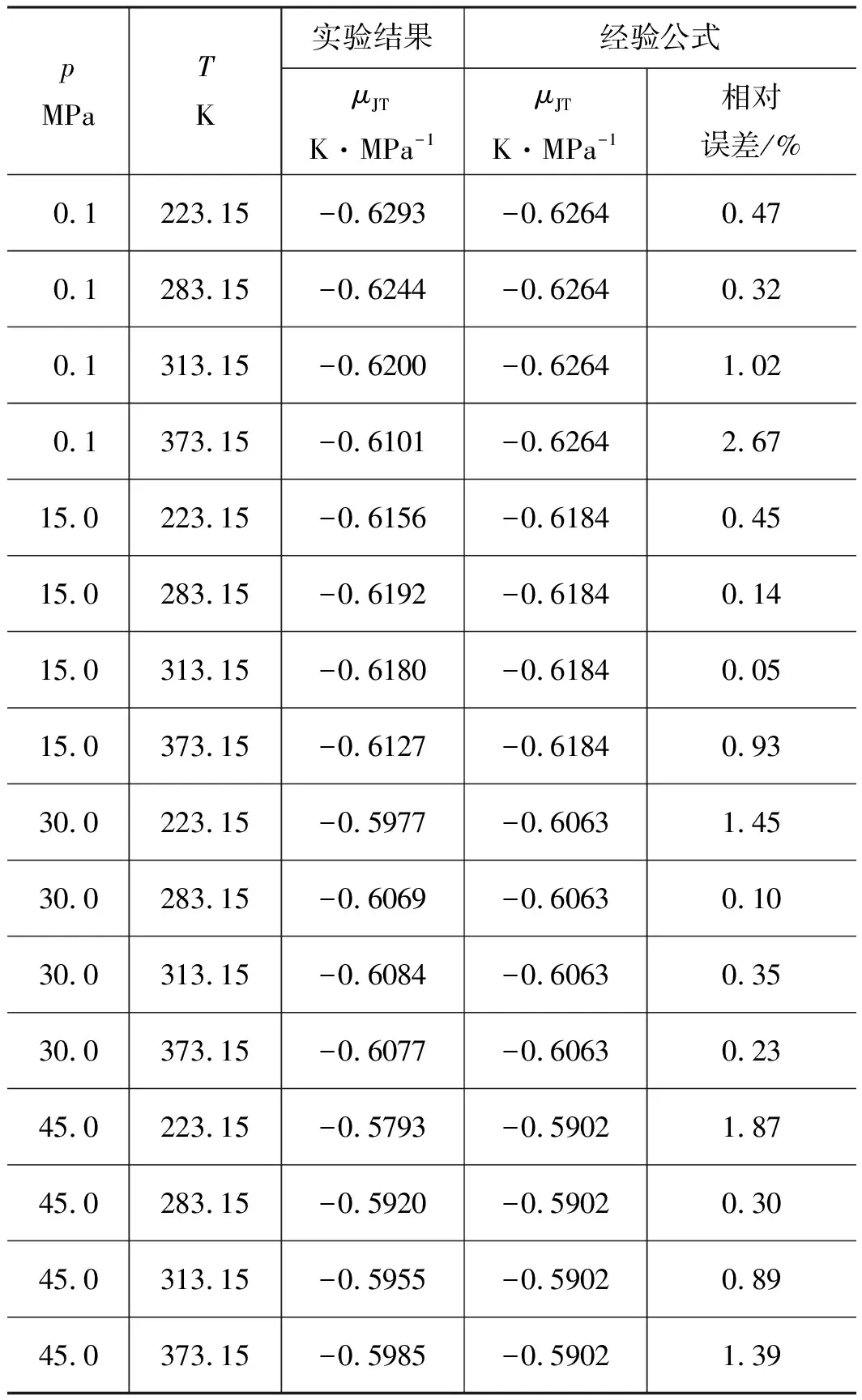
表2 实验结果和经验公式计算结果对比Tab.2 Comparison of experimental data with results of empirical equation

2 节流温升计算

将高压氦气节流过程视为等焓节流膨胀过程，则节流温升只考虑焦耳-汤姆逊效应引起的温度变化即可。在计算过程中，焦耳-汤姆逊系数采用精度较高的经验公式法，节流温升计算式如下：

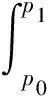
(22)

式中,T1—— 节流后温度，K

T0—— 节流前温度，K

p1—— 节流后压力，MPa

p0—— 节流前压力，MPa。

对式(22)进行积分，转化如下：

ΔT=0.6264(p0-p1)-2×10-4×

(23)

在航天高压氦气使用过程中，一般可通过压力传感器或压力表获取节流前后气体压力，代入式(23)即可计算出节流温升。

为验证经验公式计算结果的合理性，设定节流前温度为常温293.15 K，选取入口典型节流工况，按照式(23)计算温升，并与实验结果进行了对比，如表3所示，表3中的实验结果根据文献[1]中等焓线获取。

根据表3可知，通过经验公式法积分求解的节流温升与实验温升偏差较小，平均相对误差约2%，最大相对误差3.33%。同样针对航天领域氦气压力和温度范围内多种使用工况进行了计算，经验公式计算结果和实验结果最大相对误差在4%以内。节流温升误差一方面来自于焦耳-汤姆逊计算误差，另一方面来自于等焓线读数误差。通过以上分析可知，利用经验公式积分法，只需已知节流前后气体压力，即可求解节流温升，该方法计算简便，计算精度较高，可更好的满足工程实际应用需求。

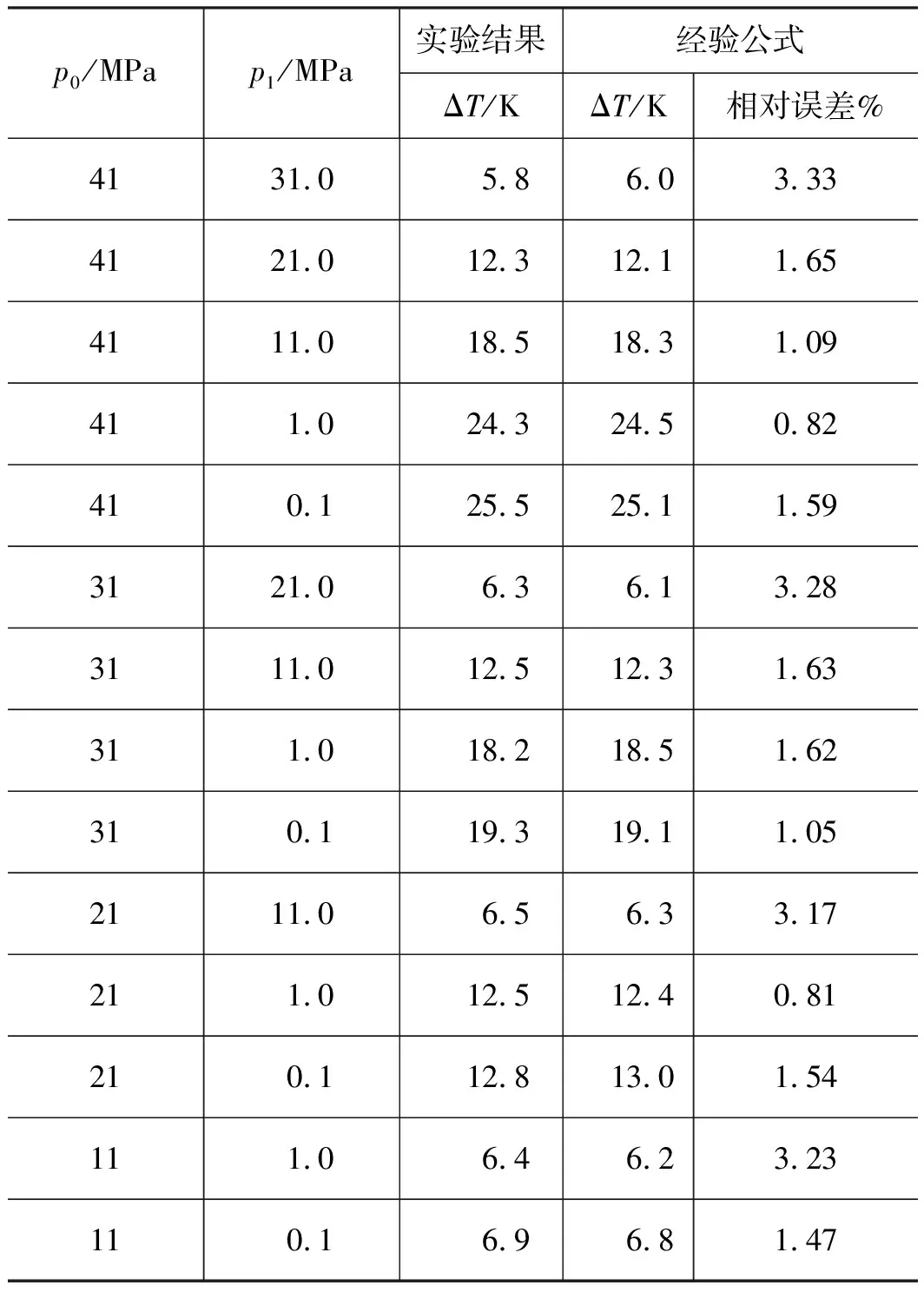
表3 温升计算结果Tab.3 Calculations of temperature rise

3 结论

本研究通过经典气体状态方程(VDW状态方程和R-K状态方程)和经验公式法推导计算了航天领域高压氦气节流过程的焦耳-汤姆逊系数，并计算了氦气节流温升，得到如下结论：

(1) 计算和实验结果均表明，常温工况下，航天领域高压氦气在节流过程中产生热效应，在进行阀门和气动系统设计时应考虑节流升温对供气元件、设备和系统的影响；

(2) 通过经典VDW状态方程和R-K状态方程推导计算的氦气焦耳-汤姆逊系数均与实验数据偏差较大，其中VDW状态方程计算结果平均相对误差约75%，R-K状态方程计算结果平均相对误差约27%；

(3) 采用经验公式计算的氦气焦耳-汤姆逊系数均与实验数据偏差较小，最大相对误差在3%以内；通过经验公式法积分求解的节流温升与实验温升偏差较小，最大相对误差在4%以内。

经验公式积分法可在已知节流前后气体压力时，求解得出节流温升，该方法计算简便，精度较高，便于解决工程实际问题。