北京地区体感温度误差订正方法研究

武略 焦瑞莉 王毅 夏江江 严中伟 李昊辰

(1 北京信息科技大学 信息与通信工程学院，北京 100101； 2 国家气象中心，北京 100081；3 中国科学院大气物理研究所，北京 100029；4 中国科学院大学，北京 100049；5 北京邮电大学 理科学院，北京 100876；6 北京大学，北京 100871)

引 言

体感温度是指人体所感受到的冷暖程度，其大小会受到诸如气温、风速、相对湿度和太阳辐射等气象要素的综合影响[1-3]。体感温度不仅直接影响各类人群的日常生活、工作、旅游等，也可影响人体健康。

体感温度属于人体舒适度研究范畴。人体舒适度是以人类机体与近地大气之间的热交换原理为基础,从气象角度评价人类在不同气候条件下舒适感的一项生物气象指标[4]。自1966年Terjung提出人体舒适度指数概念以来，发达国家相继开展了广泛深入的研究，并提出了诸如风效指数、不适指数、温湿指数等不同的生物气象指标[5]。在1980s我国有关舒适度的研究还只是一些定性的描述，直到1990s开始才取得较快的进展。气象领域人体舒适度指数研究基础和关键在于体感温度的研究[6]。目前，对体感温度的预报多为基于数值天气预报模式预报的温度、风速和相对湿度的结果计算得到[7]。因此，对体感温度的预报能力取决于数值天气预报对温度、风速和相对湿度等气象要素的预报能力。过去40 a数值天气预报的预报水平不断提高[8],但由于大气系统存在混沌行为、人们对天气气候系统的物理机制认识不够、以及对外强迫的不准确描述等原因，导致数值天气预报的不确定性[9-10]，所以难以做到绝对准确。

受制于数值天气预报对单一气象要素的预报不确定性，对多气象要素非线性组合得到的体感温度预报也存在不确定性，数值天气预报需要模式后处理方法来提高对气象要素的预报能力。利用统计方法如模式输出统计MOS[11]、相似集合AnEn[12]、卡尔曼滤波KF[13-14]等,可在数值天气预报模式预报的变量和目标预报量之间构建一个统计关系，以此对数值模式输出结果进行后处理订正预报，这种方法结合了物理模拟(数值模式)和数据驱动(统计方法)的优势——以物理模拟来实现对环境大气趋势的预测结合数据驱动来实现对高分辨率局地特征的统计，在一定程度上可以提高数值天气预报对气象要素的预报能力。

机器学习可以在不完全理解物理过程的情况下得到结果，以及可以相对容易的处理多种不同的数据源，机器学习对科学和技术的发展越来越重要[15]。近年大量气象研究工作中应用了机器学习方法[16-18]。机器学习也被作为后处理技术提高数值天气预报模式的预报能力[19-21]。

本研究旨在基于欧洲中期天气预报中心(ECMWF)数值天气预报模式的输出，利用机器学习算法提高对体感温度的预报。第24届冬奥会、冬残奥会于2022年在北京城区、延庆赛区和河北张家口赛区举行。冰雪运动项目与气象条件关系密切，同时冬季户外大型赛事也对气象服务提出了严苛要求，作为气象服务中的体感温度预报可为运动员、服务人员和观众提供直观的冷热感觉参考，具有现实意义。因而本研究选择北京地区为目标研究区域，并着重研究冬季体感温度的预报。

1 体感温度计算方法及资料介绍

1.1 体感温度经验计算公式

体感温度主要受温度、风速和相对湿度等气象要素的综合影响，在以往的研究中已有广泛的认识[22-23]。研究使用的是吕伟林[1]的体感温度经验计算公式，该公式以温度、风速、相对湿度和太阳辐射来计算体感温度，具体为：

Tg=T+Tu+Tf+Tr。

(1)

式中：Tg为体感温度；T为气温；Tu为空气相对湿度修正项；Tf为风速修正项；Tr为太阳辐射修正项。

(2)

其中：u为相对湿度，而ut定义为静风、非太阳直射条件下体感温度等于气温时的相对湿度：

(3)

风速修正项Tf为：

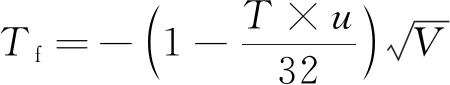
(4)

其中：V为风速。

太阳辐射修正项为：

Tr=0.42Ca(1-0.9Mc)Ia，

(5)

式中：Ca为所着衣物对太阳辐射的吸收能力，衣物颜色越深，吸收辐射能力越强，对体感温度的增益效果越高。从夏季多数人衣着颜色偏浅、冬季多数人衣着颜色偏深这一特点考虑，夏半年Ca定为0.4,冬半年Ca定为0.75；Mc为云量系数,云量越多,辐射增温效果越弱,由于站点观测中并没有云量资料，所以使用降水资料进行代替，晴天时为0，降水时为1.0；Ia为辐射增温系数，其中夏季为1.2，春、秋季为0.9，冬季为0.4。

1.2 站点数据及缺失数据插补

采用2015年1月—2017年11月北京地区20个气象观测站的逐小时气温、相对湿度、风速数据，基于该数据用公式(1)计算体感温度作为真值数据(机器学习标注数据)。站点详细信息及缺失(或异常)数据占该站点所有数据比例如表1所示。由表可见，北京地区20个气象观测站的数据存在不同程度上的缺失，约2.0%～5.0%。需要对缺测资料进行必要的数据插补，才能保证资料的连续性。对于缺测资料的恢复，常使用邻站未缺测资料进行比较其差值，基于差值进行恢复。或者利用相邻年份资料做线性内插来恢复[24]。选取1个站点连续3 d的气温变化数据，可以直观的发现数据的缺失，如图1红色实线所示。

为了能更充分地利用数据，使用缺失数据前后的正常数据构造插值函数，如下：

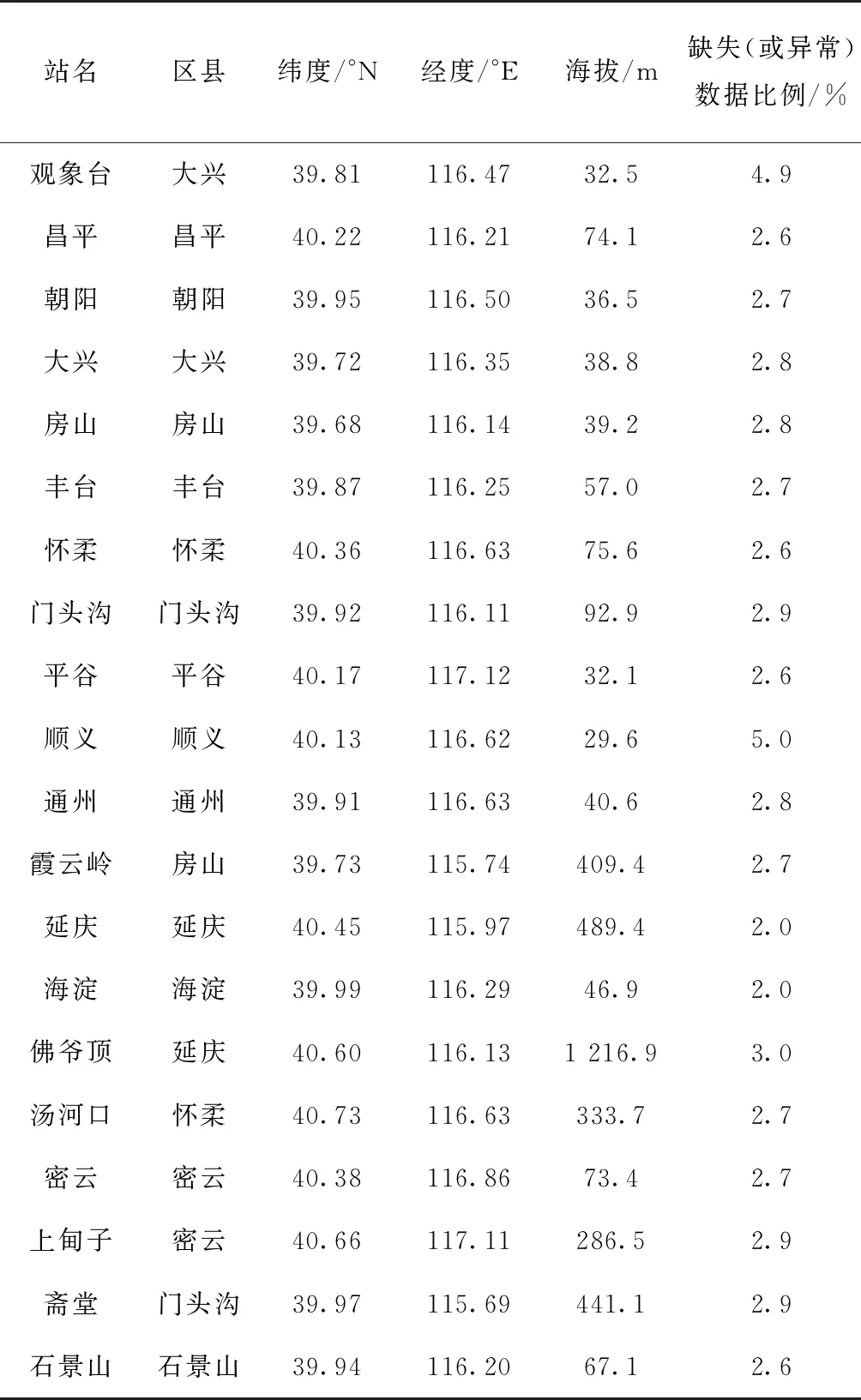
表1 北京地区20个气象观测站信息Table 1 Information of twenty meteorological observations stations in Beijing

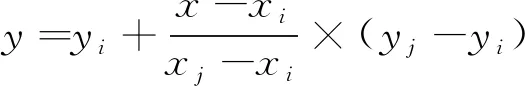
(6)

其中：(xi,yi)和(xj,yj)分别表示缺失值前后的时间和气象要素数值，建立线性模型，然后对缺失时刻进行插补，得到了较好的结果，如图1蓝色虚线所示。

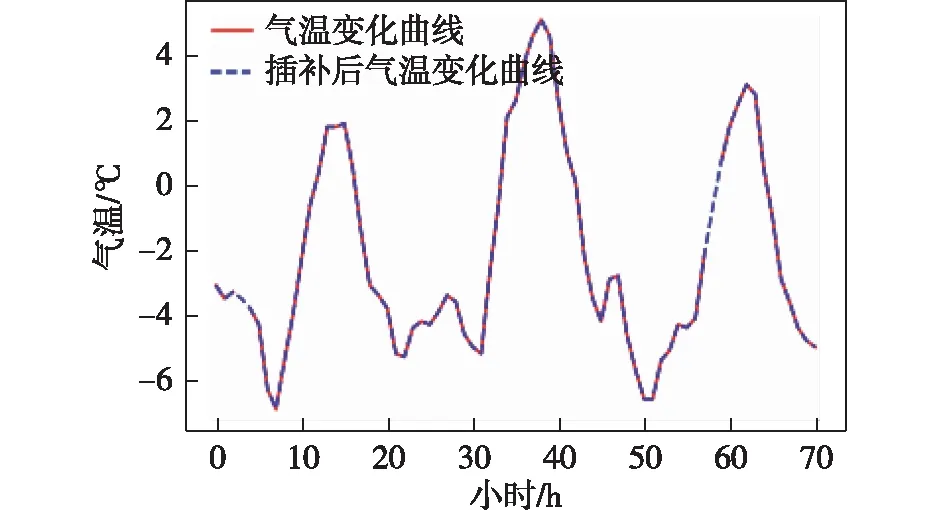
图1 插补前后气温变化对比图(以2015年1月1日00时(世界时,下同)—3日23时为例)Fig.1 Comparison of temperature changes before and after interpolation(0000 UTC on January 1 to 2300 UTC on January 3, 2015)

1.3 ECMWF模式预报数据

模式预报数据使用欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts，ECMWF)数值天气预报模式输出气象要素。每天按照所使用的初值分为00时(世界时，下同)与12时给出2个时次的预报，时间分辨率为：0～72 h逐3 h分辨率、72～240 h逐6 h分辨率；空间分辨率中近地面分辨率为0.125°×0.125°，高空分辨率为0.25°×0.25°；时间范围为：2015年1月—2017年11月；空间范围选华北地区(35°～45°N，110°～ 120°E)。

考虑到世界时和北京时存在8 h时差，本研究把ECMWF数据时间和观测时间做了匹配，将北京时转换为ECMWF数据对应的世界时。

选取44个预报气象要素，包括地面层预报场包括2 m温度、2 m露点温度、表面温度、10 m东西风、100 m东西风、10 m南北风、100 m南北风、海面温度、大气柱水总量、大气柱水汽总量、平均海平面气压、零度层、总云量、低云量、预报反照率、对流有效位能、降雪量、雪深、总降水量、大尺度降水；气压层预报场包括500、850 hPa的温度、东西风、南北风，500、850、1 000 hPa的相对湿度、比湿、散度、垂直速度、位势高度、位势涡度。

2 方案设计

研究设计了3种方案进行对比试验，分别分析3种方案的预测效果，以选择最优方案进行体感温度的预报：

方案一为利用模式预报的气温、风速、相对湿度直接计算体感温度作为预测结果，此方案为参照方案；

方案二为将ECMWF输出的44个气象要素作为机器学习模型的输入X，站点观测计算得到的体感温度作为模型的输出Y，构建两种机器学习模型(多元线性回归和梯度提升回归树)进行预测；

方案三为使用ECMWF输出的气象要素组合首先计算出体感温度，再使用MOS方法进行统计预报。因MOS方法作为经典的模式后处理订正方法[11]应用最为广泛，此方案定义为基于传统统计方法做预测的代表性参照试验。

2.1 数据集构建

如上所述，方案二使用的是机器学习算法构建模型，对其构建相应的机器学习数据集，将1.2节中处理得到的代表真值的体感温度作为监督学习中的标注(label)。

BNP属于多肽类激素一种，是心血管系统的一种具有生物活性的重要激素，能在心肌受损时快速入血进行调节，能够灵敏的反映出心肌受损的情况［6］，并且与心肌受损程度正相关，心肌损伤越严重BNP水平越高，它是一种常用且有效的心衰检测指标。目前BNP已被纳入心衰诊断指南，用于心衰患者的预测和诊断工作。本研究中，钩藤人参高剂量组BNP水平与卡托普利组BNP水平相近，并明显低于模型组，说明钩藤人参高剂量组在降低HCHF大鼠BNP水平，改善心功能方面效果显著。

图2 GBRT示意图Fig.2 GBRT schematic

将每套数据集分为训练集和测试集。训练集用于生成预测模型，测试集进行实际预测。以2015年1月16日—2017年1月19日的数据集作为训练集(占数据集93%)，2017年1月20日—3月13日的数据集作为测试集(占数据集7%)。实际需要用到的预报时效是从最近的起报时间开始第12～72 h逐3 h间隔和第78～240 h逐6 h间隔共49个时效(舍弃3 h、6 h、9 h是考虑了北京地区获得ECMWF模式预报数据的计算和传输延迟)。

2.2 算法模型和检验方法

2.2.1 模式输出统计预报方法

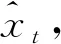
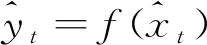
(7)

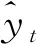
2.2.2 多元线性回归(Linear Regression，LR)

线性模型利用输入特征的线性函数进行预测，是回归问题最简单也是最经典的线性方法。对于回归问题，线性模型预测的一般公式如下：

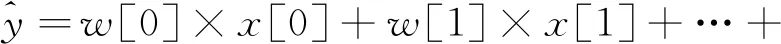
(8)

2.2.3 梯度提升回归树

梯度提升回归树(Gradient Booosting Regression Tree，GBRT)是由Friedman[28]提出的一种迭代的决策树算法，该算法的基本思想是通过构建M个弱学习器，经过多次迭代最终组合而成一个强学习器[29]。GBRT作为回归树的一种，相对于一般决策树算法具有防止过拟合、泛化能力较强等优点。

模型预测的时候，对于输入的一个样本实例，首先会赋予一个初值，然后会遍历每一棵决策树，每棵树都会对预测值进行调整修正，最终的结果是将每一棵决策树的结果进行累加得到的最后得到预测的结果，如图2及公式(9)所示，

F(x)=F0+β1T1(X)+β2T2(X)+…+
βMTM(X)，

(9)

其中：F0为初值；β为权重系数；T(X)为每一颗决策树的结果。

GBRT有两类重要的参数；一是Boosting框架的重要参数，二是弱学习器即CART回归树的重要参数。本文主要使用了第一类中的n_estimators(最大的弱学习器个数，即迭代次数，过小会欠拟合，过大又容易过拟合)、learning_rate(每个弱学习器的权重缩减系数，即步长，此值较小意味着需要更多的弱学习器的迭代次数)，以上两个参数要一起调试，开始选择一个较小的步长来网格搜索最好的迭代次数，改变步长再次网格搜索，针对本文中的数据集，n_estimators和learning_rate分别设置为240和0.01。还设置了subsample(子采样率，GBRT采用的是不放回抽样)，取值为1时，代表所有样本都采用，即没有进行子采样；小于1时可以减小方差，防止过拟合，但也会增加样本拟合的偏差，同样对其进行网格搜索，定为0.6。对于CART回归树的参数，最大特征数max_features默认为None，这是因为本文输入的气象要素特征为44个，特征数不多为None时即考虑所有的特征数；决策树最大深度max_depth设置为取决于样本和特征的数量，一般为10～100，具体数值取决于数据的分布，包括样本量和特征量，本文设置为13。叶子节点最少样本数min_samples_leaf限制了叶子节点最少的样本数，也受样本数量级的影响，设置为10。其他参数均为默认。

在进行调参时，首先从n_estimators和learning_rate进行调试，控制learning_rate对n_estimators进行网格搜索；再对max_depth和min_samples_leaf进行网格搜索，得出最优值；由于本文的特征数较少，可直接将max_features设置为None；最后考虑子采样网格搜索，得到subsample的寻优参数。而在实际问题的应用中，调参虽然会获得更好的预测结果，但也会消耗较多的调参时间，如何选择合适的算法使相关问题得到又快又准确的解决也是机器学习乃至人工智能面临的一个挑战。

2.2.4 检验方法

为了更好地评价预测体感温度的各个方法与算法，我们采用均方根误差来对预测结果进行检验。均方根误差(Root Mean Square Error, RMSE)是观测值与真值偏差的平方与观测次数比值的平方根，是回归任务最常用的性能度量。

(10)

其中：f为所采用的算法模型；D为划分的数据集；K为数据集D的样本总数；xk为第k个样本的输入；yk为第k个样本的标记(对应本文中的体感温度)。

为更好的观察预测结果，将LR、GBRT、MOS分别与ECMWF的均方根误差进行比较，定义3种算法的结果为Rn,ECMWF的结果为Re,可得提升效果R的计算公式如下：

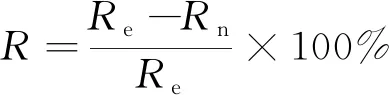
(11)

3 结果与分析

3.1 预测结果

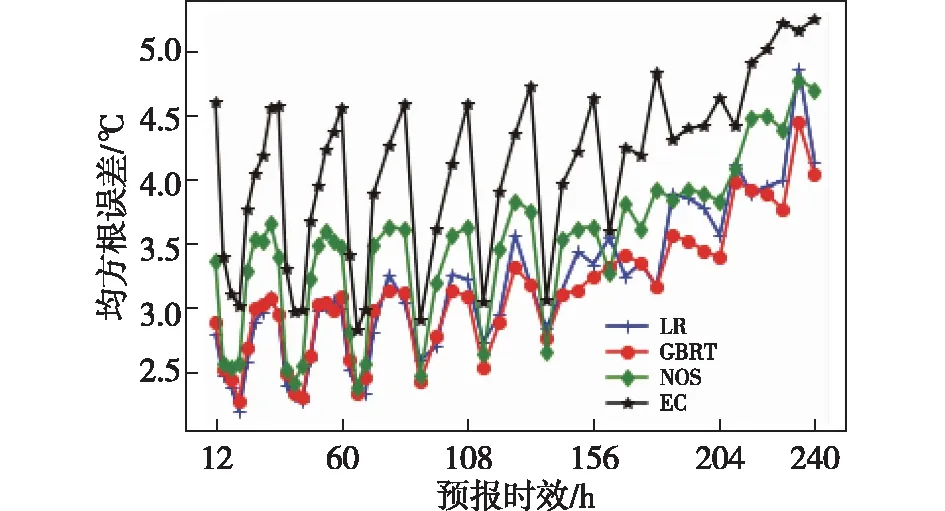
图3 ECMWF、MOS和两种机器学习模型的预测均方根误差随预报时效的变化Fig.3 Prediction of RMSEs for ECMWF, MOS and other two machine learning models with forecasting time

用4种方法分别对49个预测时效进行预测，分别计算均方根误差并将20个站点的结果平均，结果如图3所示。基于LR、 GBRT、 MOS和ECMWF模式预报得到的平均RMSE分别是3.12、3.06、3.45、4.06℃。即线性回归和GBRT明显优于其他两种，传统的MOS对ECMWF的提升效果只有15%；总体而言,随着预测时效的增长，4种方法的均方根误差都呈现增大态势。

从时间上分析，均方根误差的分布可分为两个阶段：当预报时效小于144 h时，4种方法的预测效果呈现稳定的日循环特征，相邻日期之间的RMSE并没有很大的差异。以ECMWF为例，当预报时效大于12 h且小于36 h时，ECMWF预报的RMSE由4.61 ℃下降到3.02℃并迅速回升到4.57℃，1 d内平均均方根误差为3.92℃。采用相同的方法计算36～60 h，平均均方根误差为3.72℃，差距较小。但若进一步分析LR和GBRT，可以看到日变化的最低点随时效增长逐渐升高，日平均均方根误差逐渐增大，即预报时效越长，预报效果越差。当预报时效大于144 h，日循环特征不再显著，这既是由于RMSE随预报时效的增大长而变大，也是因为20个站点的预测效果不同，两者共同作用导致进行平均处理后就抵消掉了日循环特征，其中LR和GBRT相比MOS较早的出现了消失现象。日循环现象是ECMWF的本身特点，因此在此基础上进行订正的3种方法也同样具有了这种现象。

从方法上分析，首先4种预测方法都遵循预报时效越长，预报效果越差这一客观事实。通过公式(11)计算3种算法相比于ECMWF的提升度，如表2所示。其次，选取机器学习方法GBRT、传统统计方法MOS与ECMWF进行比较：在12～72 h短期预报范围内，3种方法预测的平均均方根误差分别为2.72、3.07和3.73℃，GBRT和MOS相比ECMWF分别提升了27%和17%；在72～240 h中期预报范围内，3种方法的平均均方根误差分别为3.29、3.69和4.27℃，GBRT和MOS相比ECMWF分别提升了22%和13%，机器学习方法预报效果变差，但仍比MOS要好，这体现出了机器学习在体感温度短中期预报这一方面的优势，也彰显了使用机器学习进行天气要素预报的必要性。

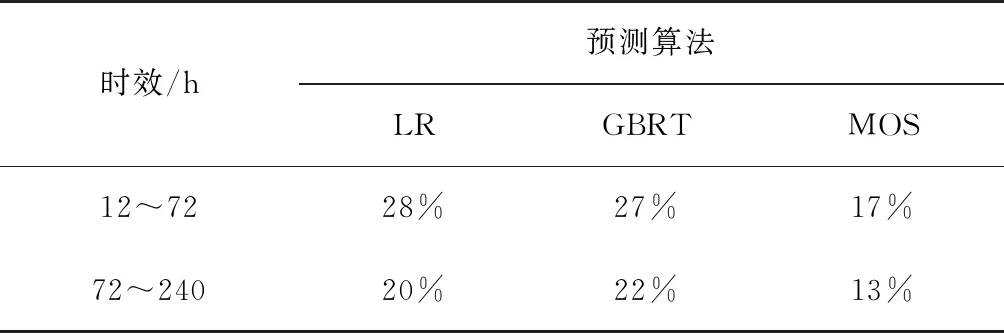
表2 3种算法提升度Table 2 The degree of improvement of the three algorithms

将20个站点的预测结果呈现在北京地区(39.6°～40.8°N，115.5°～117.2°E)，如图4所示，可以进一步观察到均方根误差随时效的增长而逐渐变大，4种方法对中长期的预报呈现疲软态势。通过统计站点的数目，可以发现其他3种方法相比ECMWF都要具有更好的预测效果，其中线性回归在12～36 h具有更好的预测能力(平均RMSE为2.70℃)，而GBRT在216～240 h中具有更好的预测能力(平均RMSE为4.01℃)，与图3中20个站点的平均结果相符。

进一步分析表明，在12～36 h和60～84 h时，ECMWF对20个站点的预报效果差异明显(图d1和图d2)，尤其北部的佛爷顶、汤河口和上甸子站点(处于40.6°～40.8°N)，均方根误差分别是9.13、8.01和5.78℃(12～36 h和60～84 h取平均，下同)，在同时段相对于其他17个站点偏高(平均RMSE为3.4℃)。在采用3种算法订正后，MOS能对3个站点起到一定的订正效果，RMSE分别是：4.55、4.02和3.50℃，LR和GBRT取得了更好的订正效果,RMSE分别是：3.02、3.13和2.75℃，2.89、3.20和2.74℃。

216～240 h时均方根误差增大，LR和MOS订正后的空间差异不明显，站点的均方根误差多分布在4～5℃。但GBRT仍存在空间差异(图b3)，以40.2°N为分界线，南部13个站点的平均RMSE为3.86℃，北部7个站点的平均RMSE为4.30℃，有明显的南北差异。

综上，3种订正方法对北京地区站点的预测效果大致呈现北差南好的态势，这是因为它们在ECMWF(也呈现“北差南好”的特点，如图d1、d2和d3所示)的基础上进行订正。而ECMWF具有此特点是因为其网格点和地面站点的高程差会导致误差[30]，同时北京的西北部多为山区，站点海拔较高，所以会出现此南北差异。

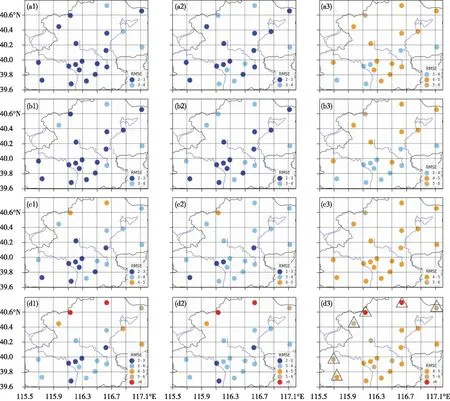
图4 (a1—a3) LR、(b1—b3) GBRT、(c1—c3) MOS和(d1—d3) ECMWF在20个站点上不同时效下逐6 h平均的预测结果(RMSE, 单位: ℃;其中高海拔站点在d3中用“△”框出): (a1、b1、c1、d1) 12 ～ 36 h; (a2、b2、c2、d2) 60 ～ 84 h; (a3、b3、c3、d3) 216 ～ 240 h Fig.4 (a1-a3) LR, (b1-b3) GBRT, (c1-c3) MOS and (d1-d3) ECMWF prediction results at 20 stations average by six hours in different models(RMSE, unit:℃; high altitude stations are boxed with “△” in d3): (a1, b1, c1, d1) from 12 h to 36 h;(a2，b2，c2，d2) from 60 h to 84 h; (a3，b3，c3，d3) from 216 h to 240 h

3.2 海拔差异

对20个站点分别进行预测时，发现预测结果在不同海拔的站点上效果不同。订正效果在高海拔站点十分明显，这一点在图4中也得到印证，即使用机器学习预测高山站有着较好的提升效果。

如图5，定义高度大于200 m的站点为高海拔站点，将高海拔站点(延庆、佛爷顶、汤河口、上甸子、斋堂、霞云岭，见图4d3)和低海拔站点(观象台、昌平、朝阳、大兴、房山、丰台、怀柔、门头沟、平谷、顺义、通州、海淀、密云、石景山)的预测结果分别取平均，可以看到对高山站使用机器学习预测体感温度获得的订正效果优于ECMWF的预报数据和MOS预测方法，这是由于在同一经纬度下，温度、气压等要素会随着高度的变化而变，但是ECMWF分辨率太低(约13 km)，其结果不能细致刻画局地地形、海拔等特征，在对高山站进行预报时就会出现较大的误差。监督学习的目的在于学习一个由输入到输出的映射，这一映射由模型来表示。简而言之，学习的目的就在于找到最好的这样的模型[31]。使用高山站点的观测数据作为标记，对模型的训练有了更准确的参考，这也是使用机器学习进行体感温度预测的目的之一。

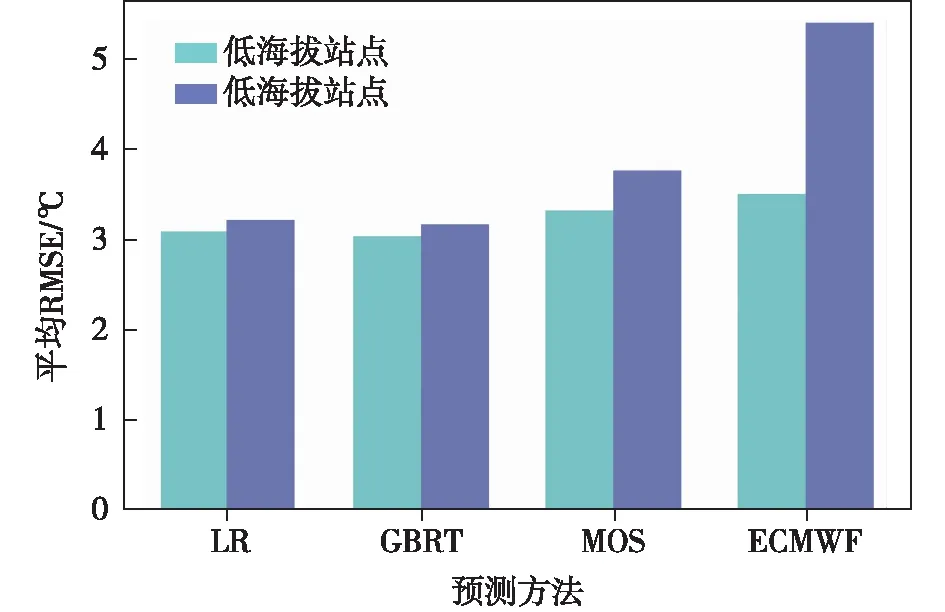
图5 高海拔和低海拔站点的预测均方根误差对比(单位：℃)Fig.5 Comparison of RMSE of high altitude and low altitude stations(unit：℃)

3.3 时效差异

图3结果表明3种算法订正效果对比ECMWF的预报数据有更好的预报效果，其中多元线性回归与GBRT的表现比较接近，因此将多元线性回归与GBRT进行单独比较(图6)。由图可见，当预报时效较短时，两种算法的准确率不相上下；当预报时效增长时，GBRT逐渐展现出优势。这是由于当预报时效较短时，线性模型在ECMWF的基础上结合站点真值已经能够最大限度地进行预测，当选取算法结构复杂的GBRT时，预测结果已得不到提升。当预报时效增长时，ECMWF的预测结果变差，结构简单的线性模型不能很好的分析数据特征，这时就需要GBRT或者其他相对复杂的算法来进一步分析数据，提取隐藏于特征中的规律，从而提高预测效果。

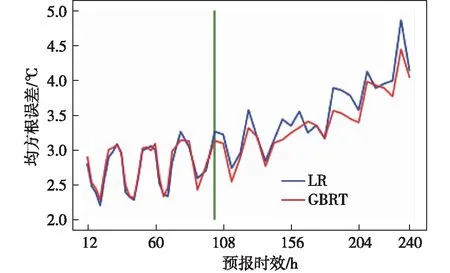
图6 LR与GBRT预测结果的均方根误差比较(单位：℃;线线表示102 h)Fig.6 Comparison of root mean square errors between LR and GBRT prediction results (units: ℃; green line indicate 102 h)

结果表明，当预报时效小于102 h(图6中绿线所处时效)，优先选择线性回归模型，因为其准确率高、易于操作、复杂度小；当预报时效大于102 h，选用GBRT模型去获得更好的准确率。

4 结论

基于气象站观测数据，结合ECMWF的模式预报数据，本文提出了基于机器学习的模式预报订正后处理思路，应用于北京地区地面体感温度预报，使用两种机器学习算法与传统MOS方法进行体感温度的订正预测并进行对比评估，结论如下：

(1)3种算法订正效果对比ECMWF的预报数据有更好的预报效果，其中多元线性回归与GBRT的表现明显优于其他两种方法，但随着预测时间的延长，预测效果都出现了不同程度的下降；针对多元线性回归和GBRT，两种算法都表现了很好的预测效果，具体应用时，可以不再使用单一的预测模型，而是根据预测效果结合模型的复杂程度进行算法选择，组建集成预报模型进行预报。

(2)在对华北地区20个站点的预测中，使用机器学习的订正效果不仅在平原地区取得了较好的效果，在高海拔站点的订正效果更加突出。一方面因为海拔变化后气温、气压等随之变化，体感温度也变化，ECMWF不能对特定高度的站点进行准确的预报；另一方面是由于监督学习的优势，站点的观测数据对模型的构建有了很好的参考。