基于迭代重加权最小二乘法的雨滴谱函数拟合研究

张宏群 陈思 周望 张晓宇 刘开辉

(1 南京信息工程大学 电子与信息工程学院，南京 210044;2 航天新气象科技有限公司，江苏 无锡 214127;3 江苏信息职业技术学院，江苏 无锡 214153)

引 言

降水是云中降落到地表液态或固态的水的总称，其中降雨是云中水汽在动力热力条件下通过宏观和微观物理过程形成并降落到地面的液态降水。单位体积内雨滴的数目随雨滴大小的分布即是雨滴谱，而雨滴谱的分布一定程度上反映了降水云成雨的过程，对于雨滴谱分布的研究是云物理学中重要的内容之一。通过雨滴谱信息可以清楚地认识降水的微物理机制并精确估测降水[1-5]。研究发现在不同的气候类型、地形条件和降水类型下，雨滴谱显示不同的分布特征。苏立娟等[6]通过对呼和浩特地区的雨滴谱特征，得到了3种不同性质降水的雨滴谱特征以及不同尺度粒子对数浓度和含水量贡献的特征。霍朝阳等[7]利用对广东龙门地面Parsivel激光雨滴谱数据进行分析，得到了降水参数与gamma函数的关系。黄兴友等[8]通过对2015—2016年南京浦口的32次不同降雨过程的Parsivel雨滴谱资料，得到了层状云、积层混合云和积雨云三类降水的微物理参量、平均雨滴谱特征和Z-R关系等特性参数。周黎明等[9]根据2013—2016年获取的山东暴雨过程雨滴谱资料，分析了三类不同天气系统影响形成的暴雨降水微结构特征。王洪等[10]针对 2015 年济南地区的液态降水过程，研究了不同云系降水的微物理参数。李晶等[11]对比分析了2018年湖南中部地区3个台站的平行观测期间雨量数据，发现在弱降水的情况下，误差较大，并分析了1次降水过程的雨滴谱形态。

Marshall，et al[12]于1948年最早提出了雨滴谱的分布为指数形式，即M-P分布，其形式为：

N(D)=N0e-λD,

(1)

其中：N(D)(单位：m3·mm-1)是单位尺度间隔，单位体积内的雨滴数；D是雨滴直径(单位：mm)；N0和λ分别是截距和斜率参数。

之后，Ulbrich[13]提出了一个修正后的雨滴谱分布形式，即gamma分布：

N(D)=N0Dμe-λD。

(2)

当μ>0时曲线向上弯曲，μ<0时曲线向下弯曲，当μ=0时公式(2)就退化为公式(1)的M-P分布，它包含3个参数，可以更好地描述雨滴谱。

由于地面雨滴谱浓度呈现指数变化，且不同粒径雨滴数量分布不均，所以使用不同的分布函数和拟合方法，拟合出来的雨滴谱差别非常大。目前对于雨滴谱函数拟合常用的方法是阶矩法和最小二乘法，但是阶矩法使用不同的阶矩组合会导致拟合出来的结果差异较大，因而选择一种合适的阶矩组合非常困难，而最小二乘法则对于测量中的误差数据，会产生过度拟合的情况。因此，本文提出基于迭代重加权最小二乘法拟合雨滴谱函数，通过比较在不同的降水条件和不同的分布函数下的拟合优度R2，最终得到了迭代重加权最小二乘法在对于雨滴谱函数拟合的可行性与普适性。

1 仪器与观测数据

采用德国OTT-Parsivel激光雨滴谱仪，2019年7—10月在海南安定获得的雨滴谱资料进行雨滴谱拟合方法研究，研究涉及的主要观测仪器及数据概况如下。

1.1 Parsivel激光雨滴谱仪

Parsivel激光雨滴谱仪是一种光学测量仪，由德国OTT公司设计生产，其测量原理是仪器上面的光学传感器组成二维光阵发射并测量激光，由接收器单元接受后转化成电信号。Parsivel中心采样面积为54 cm2，采样间隔为 1 min，可同时测量降水粒子的粒径与下落速度，粒径与下落速度分别以32档量化输出。测量粒子最大尺度为25 mm，最大下落末速为20.8 m·s-1，依据非等间隔将粒径—速度通道分为32×32档，共计1 024档，实际测量粒子尺度为0.312 5～25.0 mm，粒子下落速度为0.25～20.8 m·s-1。

1.2 观测数据

德国OTT-Parsivel激光雨滴谱仪安装在海南安定(19°68′N，110°31′E)，属热带季风海洋性气候[14]，年降水量相对于国内其它地区较大，除热带气旋直接导致的暴雨外，一些特殊的天气系统也会引发降水强烈、时间持久的暴雨过程，其中一类就是秋季由冷暖系统相互作用引发的暴雨过程，而且由于副热带高压控制，空气与云层都是呈现下沉的趋势，所以云层相对于其他地区偏低。

2019年7—10月雨滴谱观测资料连续性较好。观测取样时间为60 s，考虑到雨滴谱仪取样面积的空间代表性较低，为保证数据的稳定性，将连续10 min的雨滴谱数据视为一个分析样本，超过20 min的持续降水过程拆分为多个样本，不足10 min的不参加分析，以此使分析样本具有一定的代表性，剔除采样时间不足10 min的样本，最后共获得3 350条雨滴谱数据。由于不同类型降水云雨滴谱特征差异较大，利用卫星和地面观测的云量、云状、云高等资料以及高空规定等压面和特性层探空资料，筛选出来了不同降水云的降水数据，最后获得样本时长为10 min的降水雨滴谱样本335组，其中层状云降水样本225组，对流云降水样本110组。

2 雨滴谱函数拟合方法

2.1 数据的处理

Parsivel激光雨滴谱仪原始测量数据存在小粒子测速误差，大粒子形变误差和量化误差。所以使用Battaglia, et al[15]的方法对Parsivel激光雨滴谱仪原始测量数据进行了订正。

由于不同直径的雨滴下落末速度不同，即在取样时间Δt内，取样体积为v(Di)SΔt，则降水粒子数浓度为n(Di)/v(Di)SΔt，数浓度分布函数N(Di)表示为：

(3)

以雨滴直径为横坐标，数浓度分布函数为纵坐标，将(Di+ΔDi/2,N(Di))标于坐标中并连接成一条曲线，用以表示不同尺度雨滴数量的多少，该曲线即为雨滴数浓度分布曲线。式中：n(Di)为取样面积内通过的直径在ΔDi间隔内的雨滴数；v(Di)为粒子下落速度(单位：m·s-1)；Δt为取样时间(单位:s)；S为取样面积(单位：m2)；ΔDi为雨滴直径间隔(单位：mm)。

2.2 现有雨滴谱分布函数的拟合方法

目前雨滴谱分布函数的拟合方法主要有阶矩法和最小二乘法。阶矩法通过计算不同阶的矩量，来求拟合函数的参数，由于其计算简单，故而在实际应用中最为广泛，但是通过分析得知，在不同的降水类型和使用不同的分布函数下，阶矩法不同的阶矩组合，会导致拟合结果出现很大的差异，这在实际研究的时候就不具备普适性，在这个情况下，一种基于最小二乘法的拟合方法被提出，但最小二乘法对于测量中存在的误差数据，在拟合时会产生过度拟合的情况。

两种拟合方法的具体描述如下：

(1)阶矩法对gamma分布的雨滴谱函数来说，定义x阶矩量为：

(4)

当选择不同的阶矩组合，通过计算3个矩量就可以求得gamma分布的3个参数；当μ=0时，就可以得到M-P分布。

(2)最小二乘法通过对gamma函数两边取对数，得到：

lnN′(D)=lnN0+μlnD-λD,

(5)

通过使拟合值与实际值之间的差值最小，来求得拟合参数，由最小二乘法，得：

(6)

当ε最小时，即可求得gamma拟合参数；当μ=0时，即可得到M-P分布。

最小二乘法对比阶矩法能够有效改善不同阶矩组合带来的拟合差异，但是在对于在拟合过程中出现的某些异常数据点，最终会存在过度拟合。

3 迭代重加权最小二乘法

针对阶矩法和最小二乘法的不足，本文提出了一种基于迭代重加权最小二乘法(Iterative Reweighed Least Square，IRLS)[16-25]，对雨滴谱两种分布函数的参数进行计算。考虑雨滴谱分布中不同粒径的数浓度呈现指数变化，对雨滴谱数据分析研究时，常采用对数浓度进行对数变换后的对数坐标进行拟合分析。

将公式(5)中的lnN0、λ、μ当做3个新的参数，考虑到实际测量中存在的误差，所以对数据点进行了估计及补偿，故公式(5)形如：

y=a+bx1+cx2+d。

(7)

将公式(7)改写成向量的形式，表示如下：

(8)

根据平差准则得到：

(9)

将公式(8)代入公式(9)中，并且令目标函数为F(X)，得：

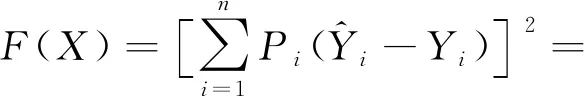
(10)

对式中Xj求偏导，可得到：

(11)

化简得：

(12)

根据通项公式，可依次求得X1、X2、X3，展开如下：

(13)

将上式改写成矩阵形式，得到：

BTPnBX=BTPnY,

(14)

由矩阵运算得待求参数为：

X=(BTPnB)-1BTPnY。

(15)

因此，迭代重加权最小二乘法的迭代计算步骤如下：

(1)通过代入初始雨滴谱浓度，求解得到初始参数X0；

(3)根据公式(9)得到新的误差，然后根据对角元素设置新的加权矩阵Pn；

(4)将新加权矩阵Pn代入公式(15)中，计算新的解Xnew=(BTPnB)-1BTPnY；

(5)重复步骤(2)—(4)，直到两次计算的参数值之差小于给定的阈值时停止迭代。

4 拟合结果的分析

为了验证本文提出的迭代重加权最小二乘法的有效性和可行性，分别用3种方法对M-P函数和gamma函数来进行雨滴谱拟合。海南安定从2019年7月11日持续降水直到7月14日，持续时间较长，但雨强不大，所以选择2019年7月14日07时08分(北京时，下同)—07时22分的层状云降水数据。2019年7月24日，该地区由于受偏东气流和冷空气的共同影响，上空产生气流辐合，为强降水提供了很好的动力条件和水汽条件。且由于白天海南岛气温回升，也给降水提供较好的热力条件，本次降水集中、瞬时雨强大，位于安定观测站的 Parsivel 降水粒子谱仪完整采集了整个降水过程的雨滴谱资料，分析本次降水过程对流云降水过程的雨滴谱特征。最后给出全部的225组层状云降水样本和110组对流降水样本的分析结果。

4.1 层状云降水的雨滴谱拟合

图1是2019年7月14日07时08分—07时22分的层状云降水数据，通过迭代重加权最小二乘法、最小二乘法和阶矩法分别进行gamma分布和M-P分布得到的拟合曲线。由图可见IRLS在对雨滴谱浓度做拟合时，无论是gamma分布还是M-P分布效果都比较好。但是也能看出在对雨滴谱浓度做拟合时，gamma分布的拟合效果相对优于M-P分布。而最小二乘法在做gamma分布拟合时还是有较好的效果，但是在进行2 mm小雨滴以下M-P拟合时，就出现了普遍的低估。这与郑娇恒[26]在分布函数选择上的研究符合，使用gamma分布函数能更好的表示各类降水谱。

阶矩法中的0/1/2阶矩、2/3/4阶矩、2/4/6阶矩在做gamma分布拟合时，就没有IRLS和最小二乘法拟合的效果好，而做M-P分布拟合时，在小雨滴1 mm出现了不同程度的高估和低估，与IRLS在进行M-P函数拟合时相比，有很大的差异，而4/5/6阶矩则无论是gamma分布还是M-P分布，都表现出了非常差的效果。这是由于高阶矩量的计算值较大，计算时会导致计算参数误差比较大。

图1 层状云不同拟合方法分别进行gamma分布和M-P分布的拟合曲线：(a)迭代重加权最小二乘法；(b)最小二乘法；(c)0/1/2阶矩法；(d)2/3/4阶矩法；(e)2/4/6阶矩法；(f)4/5/6阶矩法Fig.1 Fitting curve of Gamma distribution and M-P distribution by different fitting methods for stratified clouds：(a) iterative reweighted least square method;(b) least square method;(c) 0/1/2 moment method;(d) 2/3/4 moment method;(e) 2/4/6 moment method;(f) 4/5/6 moment method

4.2 对流云降水的雨滴谱拟合

图2是2019年7月24日18时40分—18时50分的对流云降水数据，通过迭代重加权最小二乘法、最小二乘法和阶矩法分别进行gamma分布和M-P分布得到的拟合曲线。由图可见，IRLS在对雨滴谱浓度做拟合时，对于gamma分布和M-P分布，与在层状云降水一样，都表现出了非常好的效果，而且相较于层状云降水，在对流云降水中，使用IRLS进行gamma分布和M-P分布拟合出来的效果整体上相差不大。但是最小二乘法在进行gamma分布拟合时就出现了非常大的差异，与在层状云降水中进行gamma函数拟合时很好的结果相反，具体表现在截距参数和斜率参数估计过大，导致在1.5 mm雨滴以后，就出现了断崖式的低估，而M-P就出现了整体上的高估。其主要原因是由于对流云降水量大，如果不增加形状因子μ，由于指数函数呈递减形式，在降水粒子较大时，会出现极大程度的低估，这与实验结果也相符。

图2 对流云不同拟合方法分别进行gamma分布和M-P分布的拟合曲线：(a)迭代重加权最小二乘法；(b)最小二乘法；(c)0/1/2阶矩法；(d)2/3/4阶矩法；(e)2/4/6阶矩法；(f)4/5/6阶矩法Fig.2 Curve fitting of gamma distribution and M-P distribution for different fitting methods of flow clouds: (a) iterative reweighted least square method;(b) least square method;(c) 0/1/2 moment method;(d) 2/3/4 moment method;(e) 2/4/6 moment method; (f) 4/5/6 moment method

阶矩法的0/1/2阶矩进行gamma分布拟合时，在2.5 mm以上的大雨滴出现了很大的低估，而进行M-P分布拟合时，在1.5 mm雨滴以上就出现了整体上的高估。而阶矩法中的2/3/4阶矩、2/4/6阶矩、4/5/6阶矩则无论是在gamma分布还是M-P分布都表现出了与IRLS拟合相差不大的效果。其原因是由于对流云降水量大，无论是低阶矩量还是高阶矩量都很大，进行计算时，反而对于参数的误差影响不大。

这也说明了在使用阶矩法时，选择合适的阶矩组合对于最后的拟合结果影响非常大，而IRLS就具有很好的普适性，无论是在层状云降水还是对流云降水，都具有一个非常好的效果。

4.3 评估结果分析

曲线拟合的评估常常采用拟合优度(R2)和均方根误差(Root Mean Square Error, RMSE)的方法来进行研究，R2的值越接近1.0，就说明拟合曲线的拟合程度越好，所以通过计算得到雨滴谱拟合曲线与实际曲线的拟合优度，从而评估整个研究结果。具体计算公式如下：

(16)

以下给出的是2019年7月14日07时08分—07时22分的层状云降水数据和2019年7月24日18时40分—18时50分的对流云降水数据以及225组层状云降水数据和110组对流云降水数据的拟合优度结果。

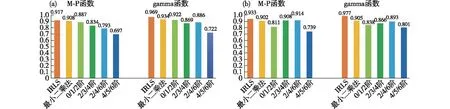
图3 一次不同降水的拟合优度值对比：(a)2019年7月14日的层状云降水；(b)2019年7月24日的对流云降水数据Fig.3 Comparison of goodness of fit values of different precipitation:(a) stratified cloud precipitation on July 14， 2019;(b) convective cloud precipitation data on July 24， 2019

图3是一次不同降水的拟合优度值对比分析，明显看出在使用迭代重加权最小二乘法的情况下，不管是层状云降水还是对流云降水，拟合M-P函数的拟合优度都达到了最优，分别是0.917和0.933；而拟合gamma函数也同样达到了最优，分别为0.969和0.977。相较于最小二乘法和阶矩法，雨滴谱浓度的拟合优度最接近1.0，这说明迭代重加权最小二乘法是具有可行性和实际性的，且使用gamma函数作为分布函数时，整体拟合优度都有显著的提高，说明gamma分布相比较M-P分布能更好地表示雨滴谱函数，而且在使用阶矩法时，中低阶量要比高阶量效果要好，这也与郑娇恒[26]的研究结论一致。

图4是225组层状云降水数据和110组对流云降水数据的平均拟合优度值对比，同样可以看到在使用迭代重加权最小二乘法的情况下，在层状云降水和对流云降水情况下，拟合M-P函数和gamma函数的R2分别达到了最优，分别是0.901、0.972和0.931、0.965。相比较最小二乘法和阶矩法，使用迭代重加权最小二乘法的效果是最好的。

霍朝阳等[7]利用2016年6—7月广东龙门地面Parsivel激光雨滴谱数据得到的层状云及对流云数据样本，评估了雨滴谱 gamma模型函数拟合方法，但是并没有对M-P函数模型做评估，且使用的是较为传统的最小二乘法和阶矩法。熊飞麟[16]提出使用M036阶矩组合进行雨滴谱函数拟合，但是只是在传统的阶矩组合上进行了调整。本文提出的基于迭代重加权最小二乘法来对雨滴谱函数拟合方法，相比较前者，不但在拟合方法上提出了有所创新，并且对雨滴谱gamma函数和M-P函数都做了试验，得到评估结果较全面。

5 结论

本文提出了一种基于迭代重加权最小二乘法的雨滴谱函数拟合方法的分析与研究，并利用Parsivel激光雨滴谱仪2019年7—10月在海南安定获得的雨滴谱资料进行试验。通过使用迭代重加权最小二乘法与最小二乘法和阶矩法分别对gamma分布和M-P分布做了拟合试验，主要结论如下：

(1)提出了采用拟合优度(R2)的方法来进行评估，R2的值越接近1，就说明拟合曲线的拟合程度越好。通过比较不同拟合方法在不同的分布函数中得到的R2，分析了在使用迭代重加权最小二乘法的情况下，R2的值最接近1，拟合曲线效果也是最好。

(2)从研究结果可以得到，在层状云条件下，阶矩法整体比迭代重加权最小二乘法和最小二乘法效果较差，主要是由于高阶矩量的计算值较大，导致计算的参数误差比较大。而在对流云状态下，由于对流云降水量大，无论是低阶矩量还是高阶矩量都很大，进行计算时，反而对于参数的误差影响不大，拟合结果都表现的很好，而最小二乘法在进行M-P函数拟合时，在粒子数较大时，会出现极大的误差，这是由于指数函数呈递减形式，在降水粒子较大时，数值非常小，如果不增加形状因子μ，会出现极大程度的低估。

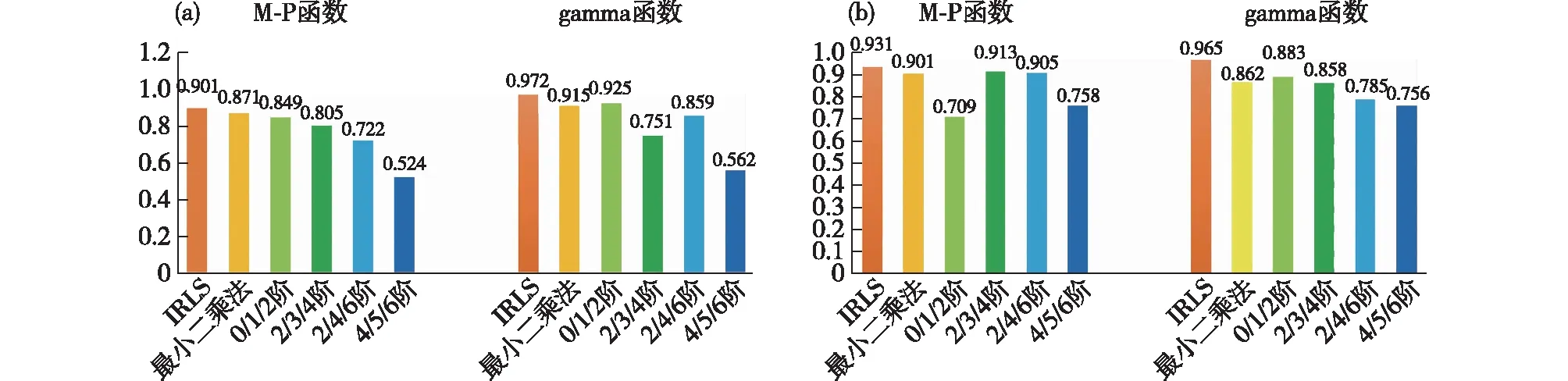
图4 225组层状云降水数据和110组对流云降水数据的拟合优度值对比：(a)225组层状云降水数据平均值；(b)110组对流云降水数据平均值Fig.4 Comparison of goodness of fit values between stratified cloud precipitation data of 225 groups and convective cloud precipitation data of 110 groups: (a) average values of stratified cloud precipitation data of 225 groups;(b) average values of convective cloud precipitation data of 110 groups

(3)得到了不同的降水类型和使用不同的分布函数条件下，最小二乘法和阶矩法的拟合效果有很大的差异，尤其是阶矩法的阶矩组合选择如果不合适，会出现极大的高估或者低估现象，而迭代重加权最小二乘法无论是在层状云降水还是对流云降水，在gamma分布函数和M-P分布函数都有较好的拟合效果，说明迭代重加权最小二乘法有较好的普适性。

通过本文的研究，相比较最小二乘法和阶矩法，使用迭代重加权最小二乘法在进行雨滴谱函数拟合时，gamma函数和M-P函数拟合都具有非常好的拟合精度，说明该方法具有较好的普适性和精确性，但同时也可以看到，在使用该方法计算拟合函数参数时，尽管设置了迭代阈值，但还是增加了一部分的计算量，这也是我们在后续研究中需要改进的地方。