伽利略新解“王冠之谜”——从密度秤到浮力天平的思维过程

仝 磊

(江苏省南京市金陵汇淳学校，江苏 南京 211316)

1 引言

阿基米德最为人们熟知的故事是解决了“王冠之谜”，因故事具有广泛的代表性和深刻的教育意义，在初中物理课堂中老师们常常会予以采用，或在“密度”一节，或在“浮力”一节。总之，教师希望借着阿基米德在具体问题情境中的深入思考，向学生展现物理探索的无穷魅力。对于阿基米德探索“王冠之谜”的故事，师生们早已耳熟能详。此外，大部分教师和学生可能还记得他的名言：“给我一个支点，我可以撬动地球”，通常在“杠杆”的教学中被老师们引用。遗憾的是，无论教师还是学生，均很少意识到这两个故事之间的密切联系，其中奥秘由另一位伟大物理学家伽利略揭开。

伽利略读到了阿基米德解决王冠之谜的故事，深为阿基米德的智慧和才能所感动，但认为他所使用的方法较为繁琐。此后，他反复阅读阿基米德关于浮力定律和杠杆原理的论述，研制了可以测定各种物质密度的小秤，使解决王冠之谜的方法变得更为简捷。[1]

2 密度秤的构造及原理

图1是密度秤的结构示意图，主要部分包括以O为支点的杠杆AB，左右两端分别有一个可自由滑动的挂钩，右侧为待测物体，左侧为配重。

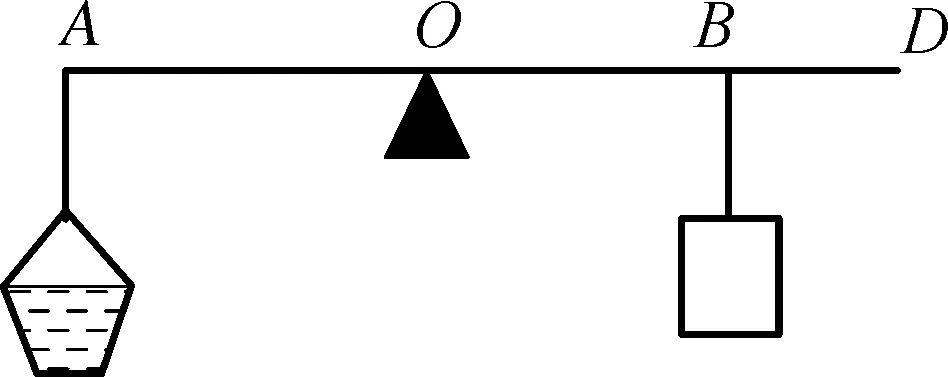
图1

调节平衡螺母使杠杆处于平衡状态，在杠杆左端A处悬挂配重，可以是细石、沙砾或者钩码，在右侧OD之间B处悬挂待测物体，使杠杆仍处于平衡状态，为减小测量误差，B点应尽量靠近D端点。紧接着，将待测物体缓慢浸入水中，将配重向支点O移动至C点(图2)，使杠杆再次平衡。

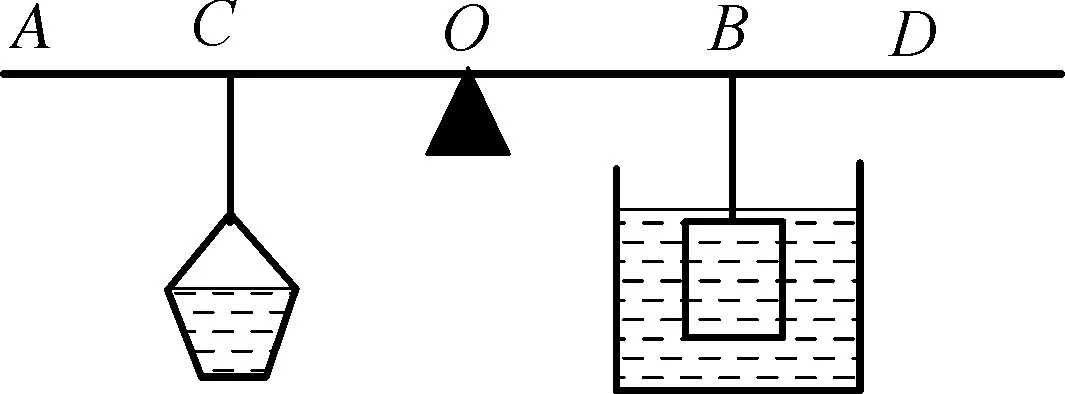
图2

根据上述原理，笔者制作了如图3所示的密度秤，具体制作材料和使用方法如下。

图3

(1) 密度秤的结构：铁架台、带刻度的杠杆(在左、右两端分别挂有一个可自由滑动的挂钩)、两个矿泉水瓶(一个作为配重，挂在左侧;一个用来浸没待测物体，挂在右侧)。

(2) 密度秤的使用:使lAO=lBO=20 cm，初始悬挂点位置一经确定后不可改动。由上述公式可在杠杆左侧标定密度的刻度，支点O位置对应的密度为1.0 g/cm3，由支点向左密度逐渐增大，呈现左密右疏的不均匀分布，刻度10 cm处对应的密度值为2.0 g/cm3，刻度15 cm处对应的密度值是4.0 g/cm3，刻度18 cm处对应的密度值为10.0 g/cm3。每次测量前调零,配重调到A点，待测物体悬挂在B处，在A瓶中增减水，使得杠杆平衡。

3 浮力天平的构造及原理

在密度秤的基础上，伽利略又设计了“浮力天平”，用它能够直接测出王冠中所含金、银的比例。[2]伽利略运用阿基米德发现的浮力原理和杠杆原理，使得“王冠之谜”变得简单易解。浮力天平的构造如图4所示，从整体上看它有点像普通的天平，秤臂有1 m多长，在两端分别刻有A、B两个凹槽，中间吊起成为支点，在距A点不远处有一段细密均匀的刻度，其两端分别标注为x、y。

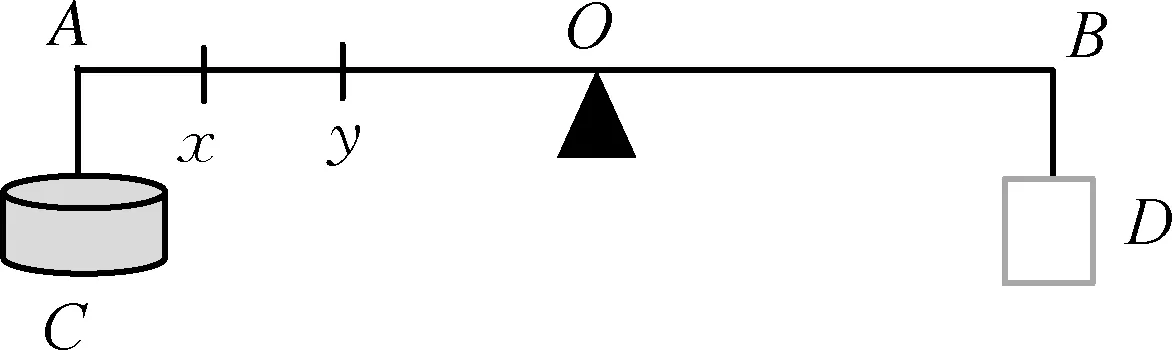
图4

秤臂上x、y的确定：在B点挂上金块，在A点挂上砝码盘，增减砝码使秤臂平衡，然后把金块浸没到水中，同时砝码盘向支点移动，当秤臂再次平衡时，砝码盘所在的位置到O点的距离就是x。取下金块，换上银块，用同样的方法确定y。

如图5所示，测量时将王冠挂在B点，砝码盘挂在A点，增减砝码使秤臂平衡。将王冠慢慢没在水中，同时将砝码盘向支点移动，当秤臂再次平衡时，砝码盘移到了x、y之间，在秤臂上记下砝码盘所在的位置到O点的距离z。

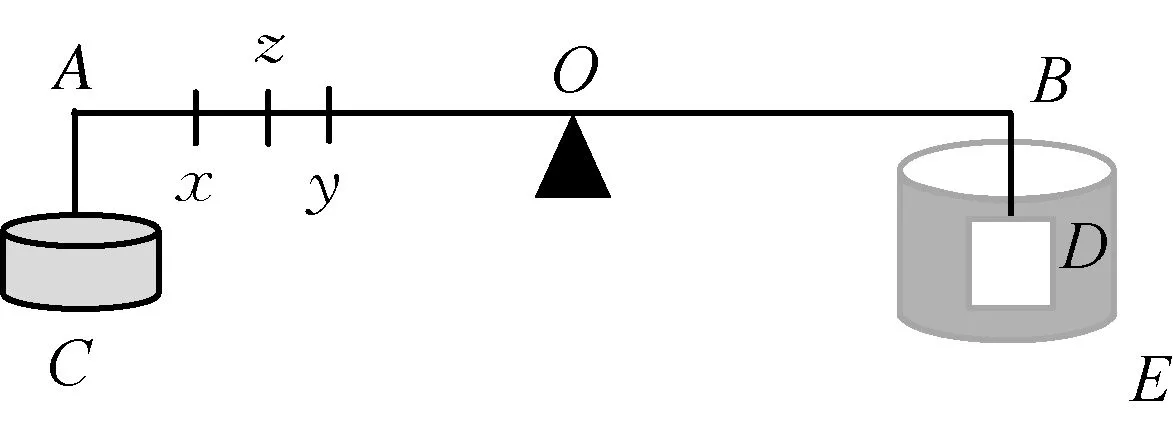
图5