不同参数取值范围下CROPGRO-cotton模型全局敏感性和不确定性分析
高浚 周保平 王昱 于晗 王君
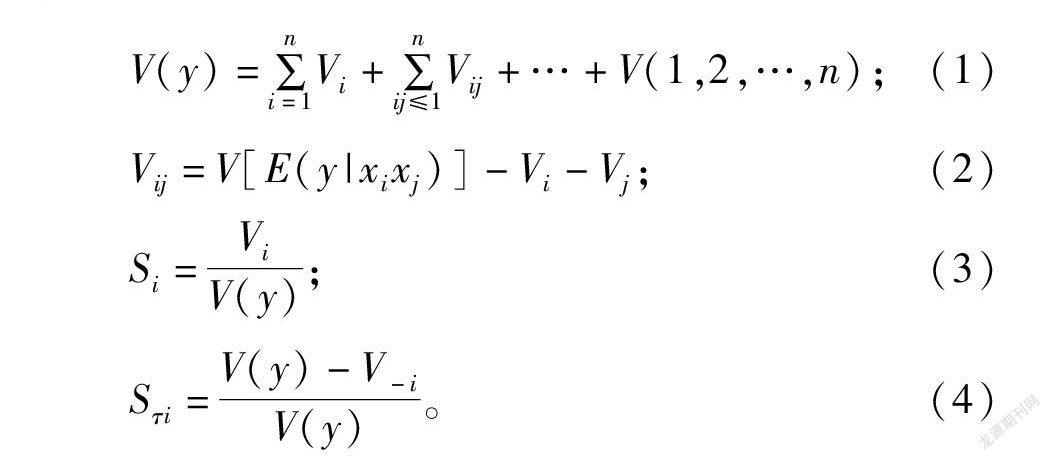
摘要:在对新作物模拟的过程中,需要对品种参数重新进行率定,但是很多参数难以测量和校正,所以需要确定参数的取值范围。目前,参数的取值范围大部分通过2种方式得到:(1)实测数据和前人文献;(2)参数初始默认值的某个百分比上下变动。前者因为很多实测数据和率定后的参数未公布,所以选择后者确定参数取值范围。在5个参数取值范围(10%、20%、30%、40%、50%)下,通过Simlab软件,采取扩展傅里叶幅度敏感性检验(EFAST)法,对不同参数取值范围的输出变量进行敏感性和不确定性分析可知,30%的参数取值范围能很好地模拟作物生长。敏感性分析与不确定性分析标明其输出变量成熟期(MDAP)、产量(HWAM)、生物量(CWAM)的一致性检验系数(TDCC)分别为0.86、0.9、0.88,P值(显著性分析)均小于0.05,具有显著一致性,开花期(ADAP)的TDCC较小,为0.66,这因为只有参数EM-FL为敏感性参数,其余参数均不敏感。模型的输出结果中ADAP、MDAP、HWAM的实测值均处于95%置信区间内,CWAM略差。本研究可帮助CROPGRO-cotton模型在南疆地区的应用提升模拟精度和模拟效果。
关键词:CROPGRO-cotton模型;敏感性分析;不确定性分析;参数取值范围;EFAST法
中图分类号: S126 文献标志码: A
文章编号:1002-1302(2022)09-0195-07
作物模型运用数学模型把天气、土壤、田间管理等体系组合成一个整体,运用计算机定量计算实现动态模拟[1],了解作物的生长情况。因为生长过程采用的是数学公式表达,所以模型输出的结果具有一定的不确定性。不确定性分析(UA)用来帮助量化试验数据和参数估值的可信度,当前运用概率分布函数来说明不确定性。敏感性分析(SA)用来量化某个不确定参数对模型输出的作用。在模型应用前,都要对模型参数进行率定,实现模型的本地化,参数的率定结果能很大程度上影响模型模拟的结果,所以,不确定性分析和敏感性分析非常重要。
当今,作物模型探索的一个关键点就是对模型品种参数、土壤参数、田间管理参数等进行敏感性分析,国内外有不少研究专家运用了各种试验方案去进行探索。例如,不同灌溉、不同气候等方法对ALMANAC模型[2-3]、WOFOST模型[4-6]、COTTON2K模型[7-9]、农业技术转移决策支持系统(DSSAT)模型[10-12]等模型实现不确定性分析和敏感性分析。但是,目前对于不同参数取值范围下CROPGRO-cotton模型[13-15]敏感性分析和不确定性分析还鲜有人研究。
本研究主要研究南疆地区的棉花,实测数据来自于南疆阿克苏地区的天气、土壤和大田数据。运用扩展傅里叶幅度敏感性检验(EFAST)法[16-17]对模型的品种参数进行敏感性分析,然后用EFAST法的输出结果进行不确定性分析,比较不同参数取值范围下模拟精度的优劣性,这为模型本地化参数的率定取值提供一定的理论和技术支持。
1 材料与方法
1.1 CROPGRO-cotton模型
DSSAT模型中包含CROPGRO模型,此模型囊括了許多作物模型,如番茄、玉米、水稻、棉花模型等。这些作物的子模型构造功能基本一样,主要模块都是田间管理模块、气象参数、土壤参数和作物品种。田间管理模块主要控制各种管理方式,如种植时间、种植方式、灌溉、施肥、收获等。气象参数主要包括每天太阳辐射量、每天最高气温和最低气温、风速、降水量、湿度等。土壤参数主要包括土壤成分、土壤有机质含量、土壤水分等。CROPGRO模型作物的模拟涉及到三大类参数:品种参数、物种参数、生态型参数。其中,品种参数的敏感性分析是重中之重。
1.2 田间试验及数据
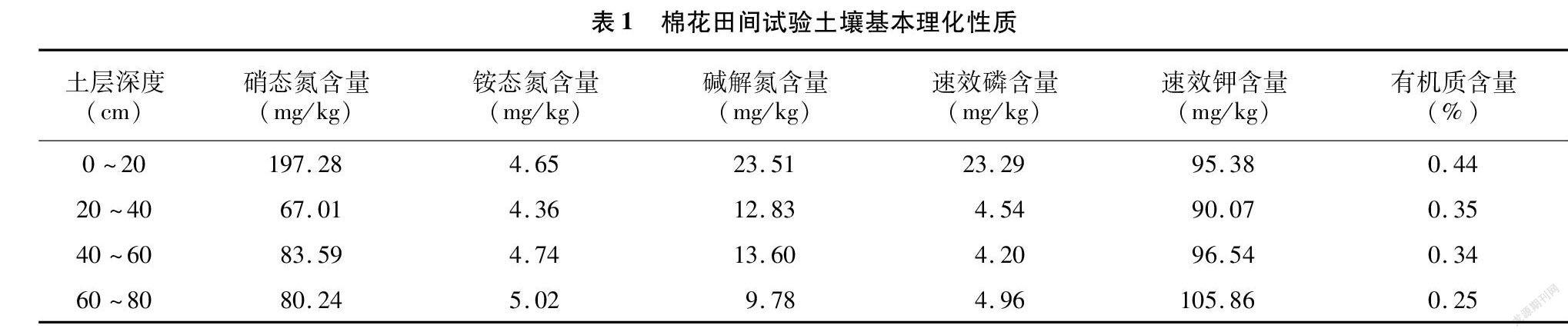
CROPGRO-cotton模型模拟所需要的田间管理及天气数据来自于新疆生产建设兵团第一师阿拉尔水利局十团灌溉试验站棉花田,位于81.31°E、40.13°N,水源充足,年均日照2 680 h,最高气温 42 ℃,最低气温-29 ℃,年平均气温14 ℃,年平均降水量为51 mm,年蒸发量2 684 mm。试验区的天气数据来源于中国气象数据网,田间管理数据来源于大田观测,土壤剖面数据来源于实际勘测,土壤的基本理化性质见表1。
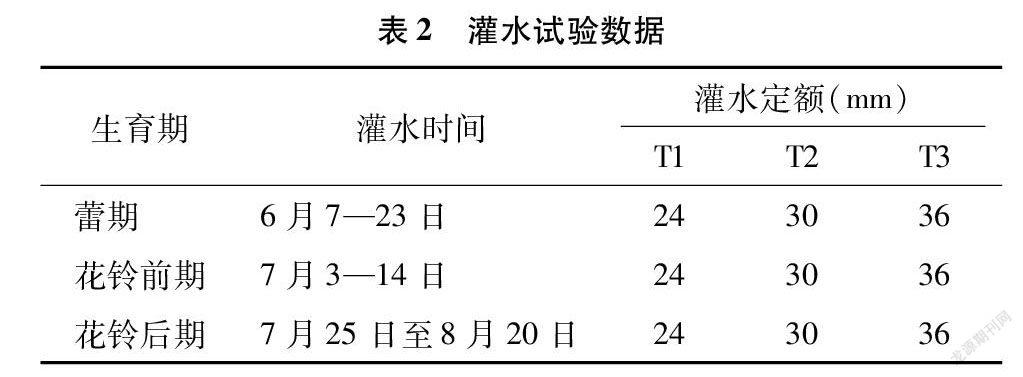
本研究的灌溉数据来源于大田试验,试验地根据棉花生育期内所需的水分不同,通过轮灌工作制度,共设计3个灌水处理,具体的灌水时间及灌水定额见表2。
1.3 模型输入参数与输出变量
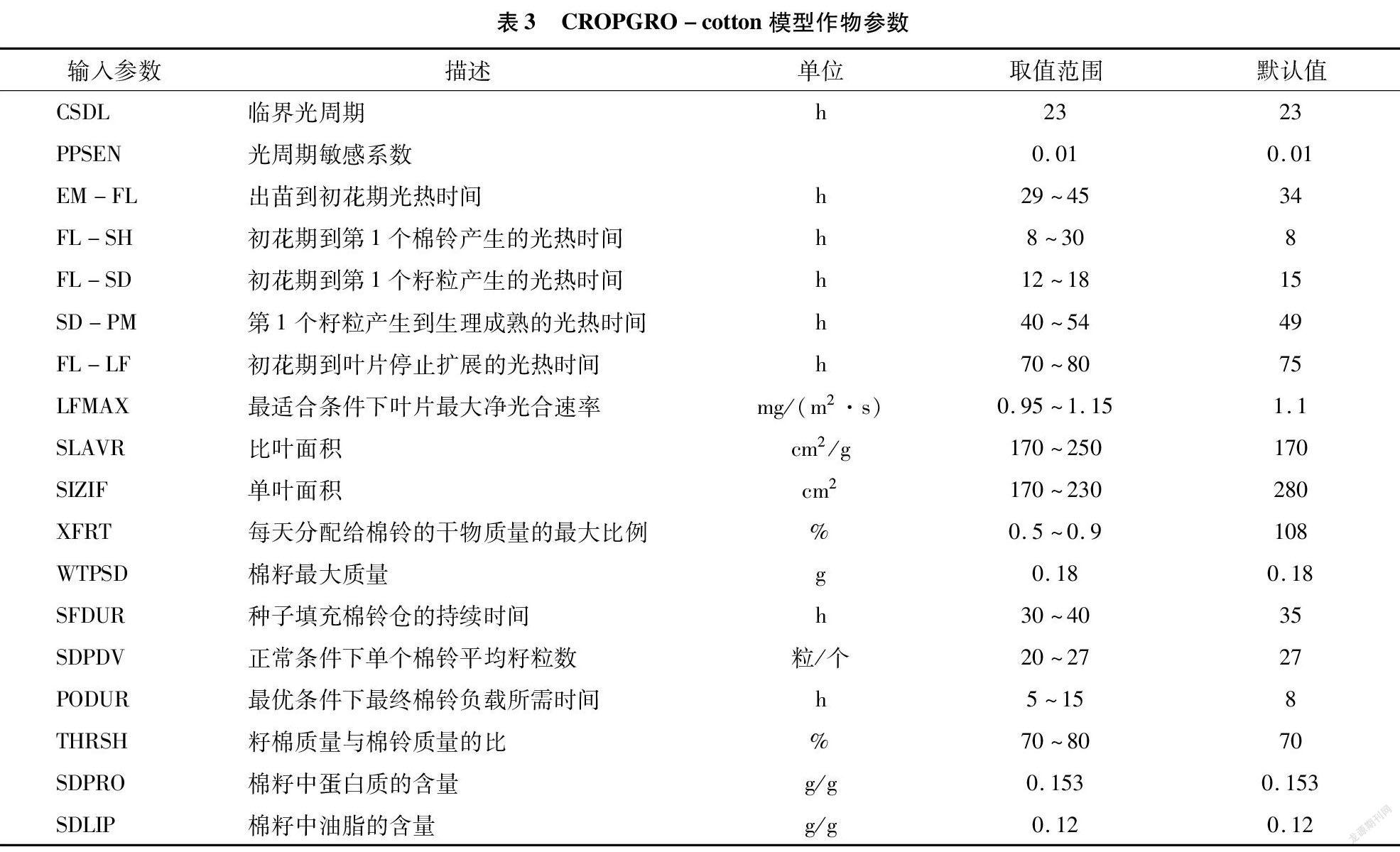
本研究选用了作物棉花的18个品种参数作为棉花的输入参数,参数值为DSSAT模型Gentype文件夹下棉花作物的默认初始值,取值范围采用DSSAT模型的参数取值范围,具体的参数情况见表3。
1.4 扩展傅里叶检验法
EFAST法是一种基于方差分解的敏感性分析方法。它通过傅里叶变换得到傅里叶级数的频谱曲线,然后用曲线获得所有参数以及参数相互作用所引起的模型方差,其计算公式为:
V(y)=∑ni=1V i+∑nij≤1V ij+…+V(1,2,…,n);(1)
V ij=V[E(y|x ix j)]-V i-V j;(2)
S i=V iV(y);(3)
S τi=V(y)-V -iV(y)。(4)
式中:V(y)为所有变量总方差;V i为第i个变量的方差;V j为第j个变量的方差;E(y|x ix j)为对于确定变量x i所对应的y的期望;V ij为变量间相互作用的方差;V -i为去除变量后的方差之和;S i为变量x i的一阶敏感性指数;S τi为变量x i的全局敏感性指数。
1.5 敏感性与不确定性分析方法
采用Simlab软件[18]输入参数名称、参数分布、参数取值范围、敏感性分析方法和抽样次数。首先,本研究设置了5种处理,EFAST法共抽样56 000次,参数取值范围分别为参数默认值(1±10%)、参数默认值(1±20%)、参数默认值(1±30%)、参数默认值(1±40%)、参数默认值(1±50%),分别记为10%、20%、30%、40%、50%,对应生成的参数样本数量分别为3 600、7 200、10 800、14 400、18 000个。其次,用R语言编写的批处理程序,进行DSSAT参数的修改、调用和输出。模型的参数取值不同时,模型的输出结果也会变化,具备了一定的不确定性,运用均值、标准差、变异系数对模型的输出结果进行评价。最后,采用一致性检验系数(TDCC)[19-20]来衡量EFAST法参数敏感性排序。
2 结果与分析
2.1 参数取值范围对输出结果影响
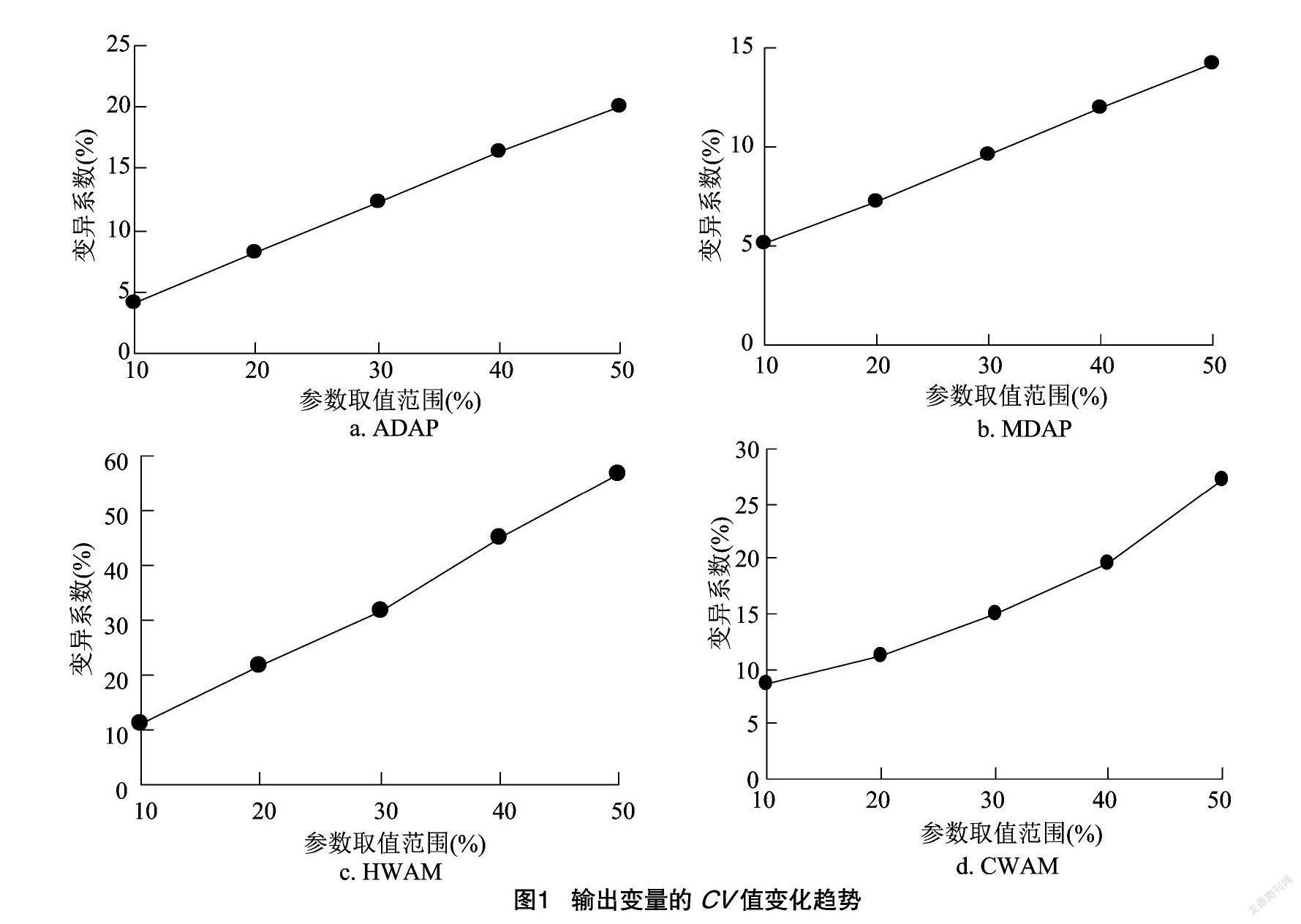
按照对应的参数取值范围,选择输出结果中开花期(ADAP)、成熟期(MDAP)、产量(HWAM)、生物量(CWAM)这4个输出变量,随后分别计算它们的变异系数(CV),其变化趋势见图1。
由图1可知,参数取值范围为10%、20%、30%、40%、50%时,ADAP的CV变化范围为4.0%~20.1%,MDAP的CV变化范围为5.0%~14.2%,HWAM的CV变动范围为10.9%~56.6%,CWAM的CV变化范围为8.7%~27.0%。当参数取值范围变大时,输出变量ADAP、MDAP、HWAM、CWAM的CV变大,呈线性相关关系。
2.2 参数取值范围对EFAST法敏感性分析的影响
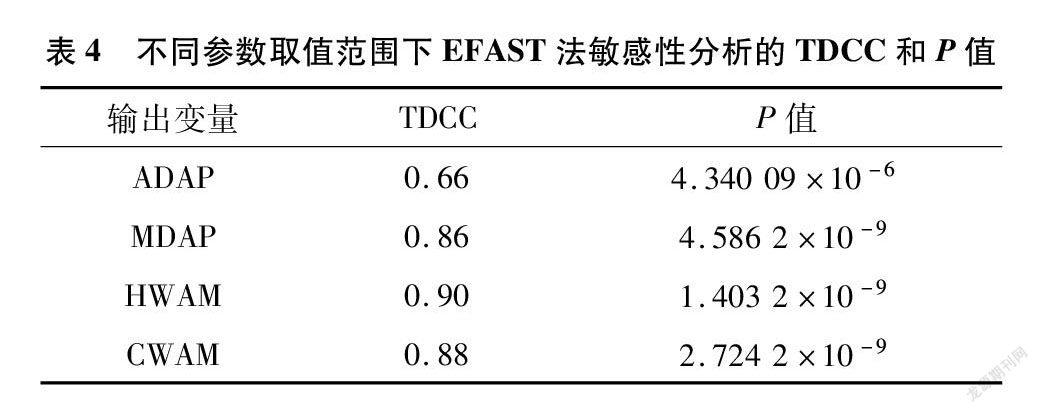
用EFAST法对不同参数取值范围下的输出变量进行敏感性分析,然后通过一致性检验系数(TDCC)对不同参数取值范围下参数敏感性排序进行评价,结果见表4。由表4可知,不同参数取值范围的P值都小于0.05,MDAP、HWAM、CWAM的TDCC都较大,但是ADAP的TDCC较小,因为只有参数EM-FL为敏感性参数,其余参数均不敏感,所以导致TDCC计算有一定的误差。说明不同参数取值范围下参数敏感性排序无明显差异。
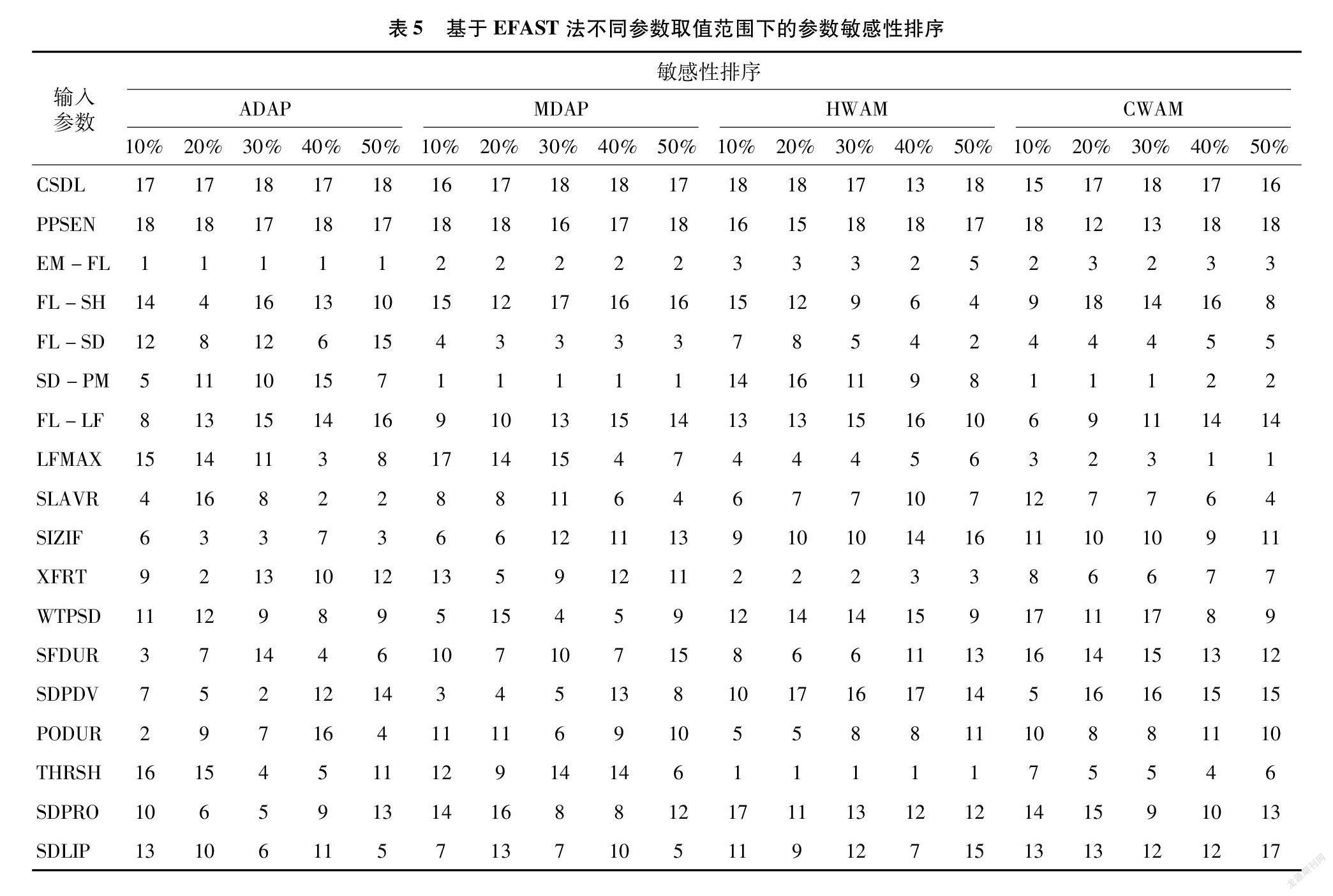
P值<0.05、TDCC较大, 只能表明参数在敏感性排序的统计意义方面有一致性,各个参数的重要程度略有不同。为了解释该问题,用EFAST法把所有敏感性指数>0.1的作为敏感性参数进行排序,具体结果见表5。
由表5可知,不管参数取值范围如何变化,在输出变量ADAP下,只有EM-FL对开花期最敏感,主要是因为现在有很多棉花品种已发展成光周期钝化品种,只有出苗到初光期的光热时间的变化会对开花产生影响。在输出变量MDAP下,SD-PM、EM-FL、FL-SD属于极敏感参数,不同参数取值范围下,排名基本无变化。在输出变量HWAM下,THRSH、XFRT、EM-FL属于极敏感参数,不同参数取值范围下,排名变化幅度很小。在输出变量CWAM下,SD-PM、EM-FL、LFMAX属于极敏感参数,不同参数取值范围下,排名稍微有些变化。CSDL和PPSEN排名变化幅度较小,不管在哪个参数范围下都属于极不敏感参数。
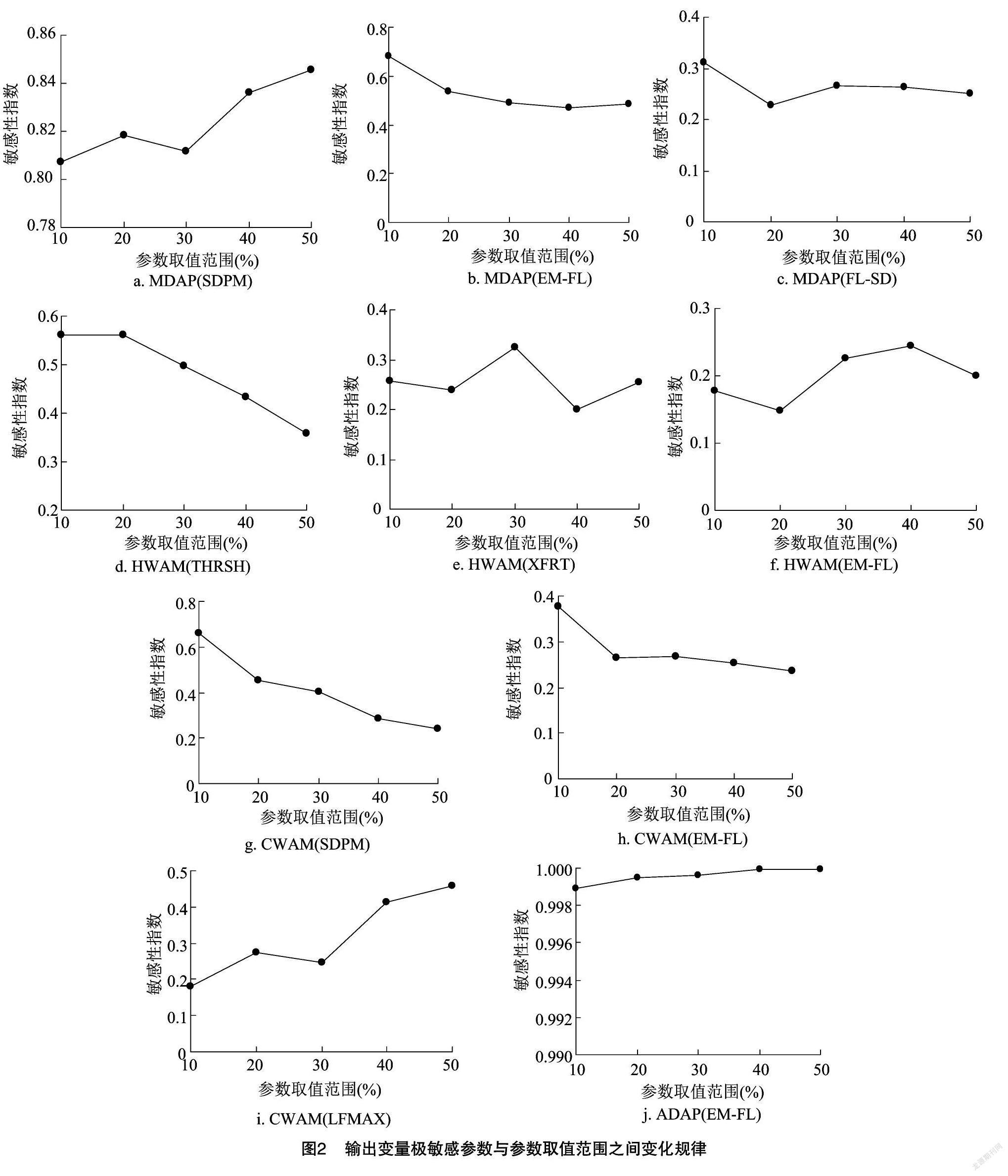
为方便研究参数敏感性在不同参数取值范围下的变化情况,把输出变量ADAP、MDAP、HWAM、CWAM中的极敏感参数提取出来,探讨它们与其取值范围之间的变动趋势,详细趋势见图2。
对ADAP来说,图2-j表明,参数EM-FL的敏感性指数在整个参数取值范围内均无明显变化。
对MDAP来说,图2-a表明,参数SDPM取值范围在50%时,敏感性指数最大,在10%~30%时,敏感性指数先增大再减小,在30%~50%时,敏感性指数逐渐变大;图2-b表明,参数EM-FL随取值范围的增大而缓慢减小;图2-c表明,参数FL-SD在10%时,敏感性指数最大,在20%时敏感性指数最小。
对HWAM来说,图2-d表明,参数THRSH在10%~20%时基本无变化,在20%~50%时,参数THRSH敏感性指数随取值范围的增大而减小;图2-e 表明,参数XFRT在30%时,敏感性指数最大,在40%時敏感性指数最小;图2-f表明,参数EM-FL在20%时,敏感性指数最小,在40%时,敏感性指数最大。
对CWAM来说,图2-g表明,敏感性指数随参数SDPM随取值范围的增大而减小,分别在10%、50%时最大、最小;图2-h表明,参数EM-FL在10%时,敏感性指数最大,在20%~50%时,变化趋势比较稳定;图2-i表明,参数LFMAX在30%时,敏感性指数会略微下降, 但在参数LFMAX的整个取值范围内总体趋势是上升的,在10%、50%时敏感性指数最小、最大。
2.3 参数取值范围对EFAST法不确定性分析影响
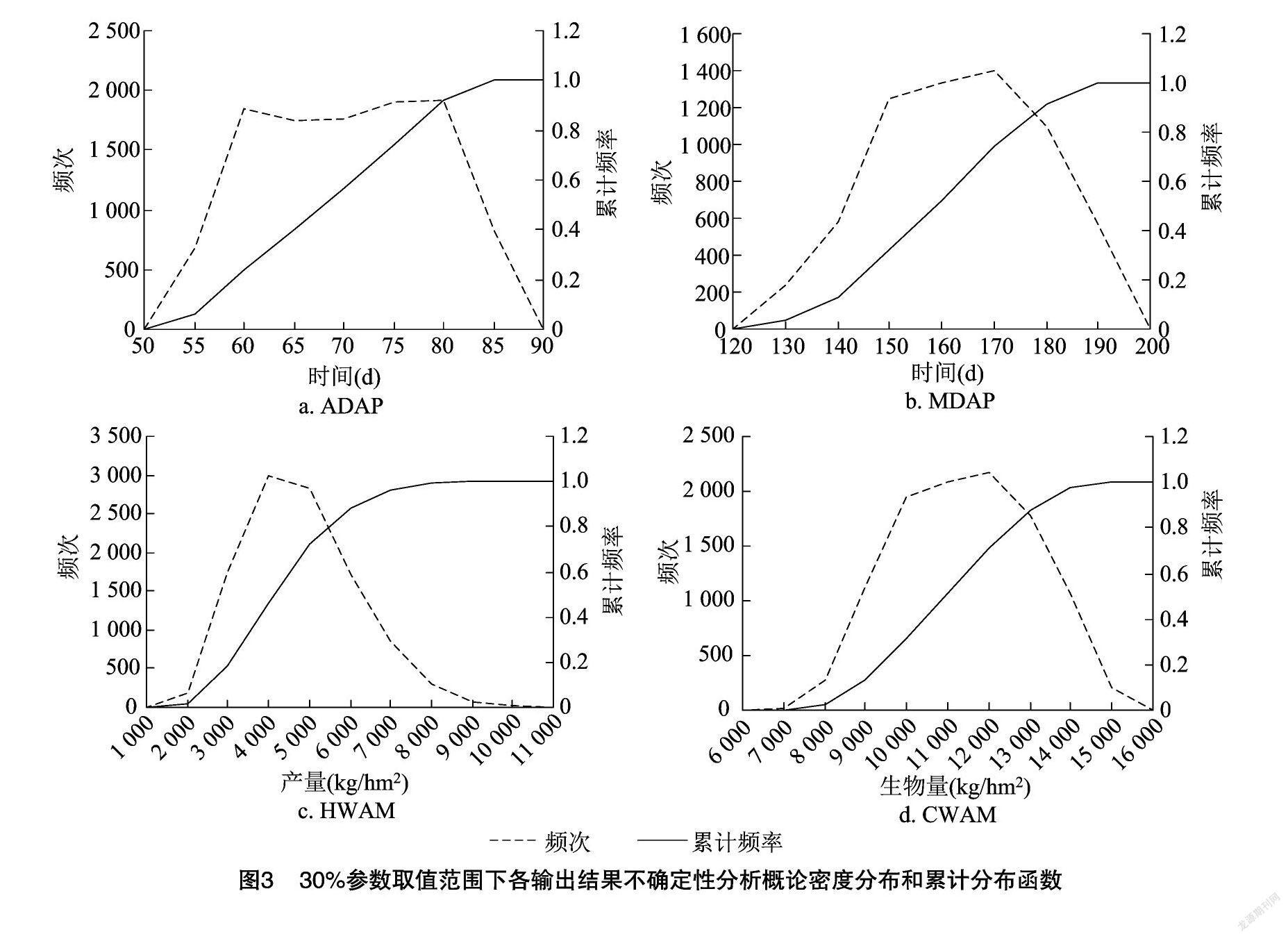
不同参数取值范围会对输出结果有不同的影响。当参数取值范围过小时,输出变量就不容易呈现出实测值的变化范围;当参数取值范围过大时,输出变量就容易和实测值不符。所以,就要通过试验筛选出一个合适的参数取值范围。本研究通过大量试验得出,当参数取值为默认值的30%时,模型的输出结果基本都分布在95%置信区间[21-22]内,模型整体模拟结果拥有比较大的可信度。模型的不确定性分析通过累计分布函数[23-24]来进行量化,具体见图3和表6。
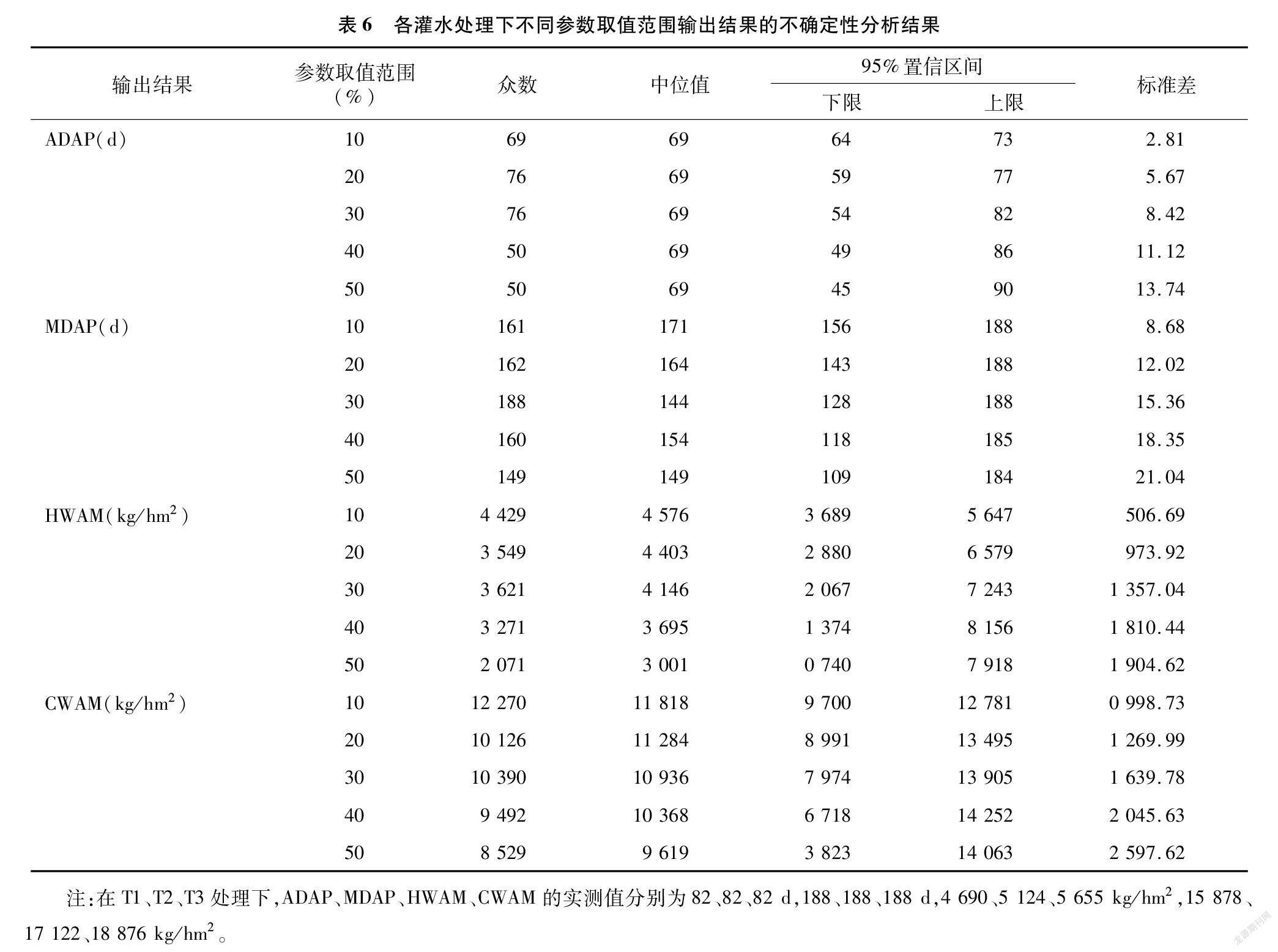
由表6可知,不同参数取值范围下各灌水处理与不确定分析结果无关。当参数取值范围为10%时,模型的输出结果中ADAP、CWAM的实测值均不处于95%置信区间内;当参数取值范围为20%时,模型的输出结果中ADAP、CWAM的实测值均不处于95%置信区间内;当参数取值范围为30%时,模型的输出结果中CWAM的实测值不处于95%置信区间内;当参数取值范围为40%时,模型的输出结果中MDAP、CWAM的实测值均不处于95%置信区间内;当参数取值范围为50%时,模型的输出结果中MDAP、CWAM的实测值均不处于95%置信区间内。
通过不确定性分析输出结果可得,在10%时,ADAP的95%置信区间为64~73 d,出现频率最高的时间是69 d,出现了416次,跟实测值相差较大;在20%时ADAP的95%置信区间为59~77 d,出现频率最高的时间是76 d,出现了420次,跟实测值比较接近;在30%时,ADAP的95%置信区间为54~82 d,出现频率最高的时间是76 d,出现了416次,跟实测值比较接近;在40%时,ADAP的95%置信区间为49~86 d,出现频率最高的时间是50 d,出现了460次,跟实测值相差较大;在50%时,ADAP的95%置信区间为45~90 d,出现频率最高的时间是50 d,出现了455次,跟实测值相差较大。MDAP的95%置信区间下限随参数取值范围的变大而减小,95%置信区间上限随参数取值范围的变大基本无变化。HWAM的95%置信区间上限随参数取值范围的变大而总体呈变大趋势,取值范围为10%~40%时95%置信区间上限随参数取值范围的变大而变大, 在50%时下降了一些。CWAM的95%置信区间上限随参数取值范围的变大而总体呈变大趋势,取值范围为10%~40%时95%置信区间上限随参数取值范围的变大而变大,在50%时同样下降了一些,说明参数取值范围在50%时,模拟情况会有比较大的误差。另外,当参数取值范围为10%时,模型模拟的MDAP有689次为0的情况;当参数取值范围为20%时,模型模拟的MDAP有2 340次为0的情况;当参数取值范围为30%时,模型模拟的MDAP有4 212次为0的情况(图3);当参数取值范围为40%时,模型模拟的MDAP有6 157次为0的情况,HWAM有451次为0的情况;当参数取值范围为50%时,模型模拟的MDAP有8 099次为0的情况,HWAM有 1 540 次为0的情况。由此可得,取值范围为30%时,模拟的效果最好,但DSSAT模型对HWAM的模拟效果略差。
3 讨论与结论
由图1可知,输出变量的CV会受到参数取值范围的影响,并且同一输出变量的CV在不同参数取值范围内呈线性增加。但是HWAM的CV过大,这可能跟参数取值范围过大有关,某些参数的取值超过了它的极限。
由表3可知,P值和TDCC显示出不同参数的取值范围对敏感性参数的排名并无显著差异,但是排名并不一样,并且最敏感参数基本完全一致。可是在敏感性分析时,当参数取值范围在10%或50%时,可能会使部分敏感性参数变成不敏感参数,由此得到一个错误的敏感性分析结果。
本研究由于低估了灌溉对棉花生物量的影响,导致CWAM的模拟效果比较差。在敏感性和不确定性分析中,应统计实测值的大概变化范围,因为当参数取值范围过小时,就不能反映出实测值的变化程度,而当参数取值范围过大时,又会大大超出实测值的变化程度,所以确定好实测值的大概变化范围,才能选择出恰当的参数取值范围。
本研究结论:(1)参数取值范围变大,输出结果的CV也会随着增大,但是它们的平均值会表现出下降的趋向;(2)不同的参数取值范围会对参数的敏感性分析结果产生一定程度的作用,即使它不会影响判别最敏感参数的个数,但是当参数的取值范围处于极端时(10%或50%),就会致使某些敏感性参数成为不敏感参数;(3)当参数取值范围太小时,输出变量就不容易呈现出实测值的变化范围,当参数取值范围过大时,输出变量就容易和实测值不符;(4)根据试验得出参数默认值±30%是CROPGRO-cotton模型敏感性分析和不确定性分析最佳参数取值范围,本研究方法可以帮助其他模型在进行敏感性分析和不确定性分析时提供对照。
参考文献:
[1]Li N,Yao N,Li Y,et al. A meta-analysis of the possible impact of climate change on global cotton yield based on crop simulation approaches[J]. Agricultural Systems,2021,193:103221.
[2]Jacot J,Kiniry J R,Williams A S,et al. Use of PhenoCam measurements and image analysis to inform the ALMANAC process-based simulation model[J]. Journal of Experimental Agriculture International,2021:120-144.
[3]刘 刚,谢 云,高晓飞,等. ALMANAC作物模型参数的敏感性分析[J]. 中国农业气象,2008,29(3):259-263.
[4]李 颖,赵国强,陈怀亮,等. 基于冬小麦农业气候分区的WOFOST模型参数标定[J]. 应用气象学报,2021,32(1):38-51.
[5]蔡 福,米 娜,明惠青,等. WOFOST模型蒸散过程改进对玉米干旱模拟影响[J]. 应用气象学报,2021,32(1):52-64.
[6]李 明. 基于WOFOST模型的春小麦产量预测方法研究[D]. 泰安:山东农业大学,2020.
[7]杨艳敏,欧阳竹,王淑芬. 基于COTTON2K的华北平原和新疆2个棉区棉花耗水特征比较[J]. 华北农学报,2012,27(增刊1):229-233.
[8]Attia A,Rajan N,Nair S S,et al. Modeling cotton lint yield and water use efficiency responses to irrigation scheduling using Cotton2K[J]. Agronomy Journal,2016,108(4):1614-1623.
[9]杨艳敏,刘小京,欧阳竹. COTTON2K在新疆棉花精准种植管理中的应用[J]. 中国生态农业学报,2005,13(3):123-126.
[10]徐瑞阳. 基于DSSAT-SUBSTOR模型的东北地区马铃薯单产模拟和种植成本效益分析[D]. 北京:中国农业科学院,2021.
[11]徐春萌,田芷源,陈 威,等. 基于DSSAT作物模型的中美大豆主产区单产模拟与验证[J]. 农业工程学报,2021,37(3):132-139.
[12]李翊尘,史培军. 基于DSSAT模型的河套平原春小麦灌溉方案优化[J]. 北京师范大学学报(自然科学版),2020,56(5):728-739.
[13]Mack L,Boote K J,Munz S,et al. Adapting the CROPGRO model to simulate chia growth and yield[J]. Agronomy Journal,2020,112(5):3859-3877.
[14]李 波,孙翔龙,姚名泽,等. 温室秸秆不同还田量条件下DSSAT-CROPGRO-Tomato模型的调参与验证[J]. 生态学杂志,2021,40(3):908-918.
[15]赵子龙. 基于CROPGRO-Tomato模型东北寒区温室番茄水分生产函数研究[D]. 沈阳:沈阳农业大学,2018.
[16]王连喜,张 阳,李 琪,等. 作物模型参数敏感性分析现状与展望[J]. 气象科技,2018,46(2):382-389.
[17]崔金涛,丁继辉,Yesilekin N,等. 基于EFAST的CERES-wheat模型土壤参数敏感性分析[J]. 农业机械学报,2020,51(12):276-283.
[18]Foscarini F,Bellocchi G,Confalonieri R,et al. Sensitivity analysis in fuzzy systems:integration of SimLab and DANA[J]. Environmental Modelling & Software,2010,25(10):1256-1260.
[19]宋明丹,冯 浩,李正鹏,等. 基于Morris和EFAST的CERES-wheat模型敏感性分析[J]. 农业机械学报,2014,45(10):124-131,166.
[20]李 波,李長信,姚名泽,等. 不同灌水处理下CROPGRO-Tomato模型全局敏感性和不确定性分析[J]. 沈阳农业大学学报,2020,51(2):153-161.
[21]Scosyrev E,Pethe A. Confidence intervals for exposure-adjusted rate differences in randomized trials[J]. Pharmaceutical Statistics,2021.
[22]Hemming K,Taljaard M. Why proper understanding of confidence intervals and statistical significance is important[J]. The Medical Journal of Australia,2021,214(3):116-118.
[23]丁润霞,黄韩亮. 正态分布概率区间模糊数及测度问题[J]. 佳木斯大学学报(自然科学版),2021,39(4):147-151.
[24]梁 骏. 水文设计值置信区间计算方法研究[D]. 杨凌:西北农林科技大学,2016.

