基于DTW-kmedoids算法的时间序列数据异常检测*
宗文泽,吴永明,,徐 计,黎 旭,王 晨
(贵州大学 a.现代制造技术教育部重点实验室;b.公共大数据国家重点实验室,贵阳 550025)
0 引言
伴随着大数据时代的到来,医学、生物、金融、工程和工业生产等领域产生了大量的具有明显的时间顺序性的数据[1-3]。尤其是生产的信息化和传感器的普及,使越来越多的数据被实时记录下来,形成了时间序列数据。在时间序列数据中,异常数据往往携带着大量有用的信息,所以时间序列数据的异常检测正在在当今社会关注度越来越高。与此同时,聚类算法作为机器学习算法的一个重要分支[4-6],不需要给数据打标签,不需要标记实例[7],成为最适合处理时间序列数据的方法之一,得到广泛研究和应用。
聚类算法一般可以用基于划分、基于密度、基于层次等方式来进行分类[8]。黄晓辉等[9]结合特征加权方法,提出了一种新的通过在子空间内最大化簇中心与其他簇数据对象的距离来融合簇内和簇间距离进行聚类的加权K-means方法(KICIC)来解决高维数据聚类问题。秦佳睿等[10]提出一种自适应选择局部半径的密度聚类算法(SALE-DBSCAN),通过确定密度峰值点,自适应选择聚类的局部邻域半径,简化了参数选择的过程;通过使用自适应选择的局部邻域半径扩张密度峰值点的邻域进行聚类,提高了聚类结果质量。季姜帅等[11]构建了融合精英保留法与轮盘赌的选择算子,并通过优化适应度函数和小生境策略保持种群多样性,加快收敛速度,提升聚类精度。时间序列聚类已经在时间序列挖掘领域引起了广泛地关注。吴永明等[12]设计了一种基于改进生长神经气模型(GNG)的自适应聚类模型,建立基于概率、范围搜寻、节点平均距离的节点生成、删除机制,实现对漂移数据实时监控。EUN等[13]提出基于谱密度[14]以及全变分距离[15]的聚类方法,通过事件的相似振荡行为构建类簇,该方法直接对时间序列数据聚类,受事件的复杂结构影响,聚类准确率低。SANDER[16]将层次聚类算法应用于时间序列的聚类上,并通过聚类有效性指标表明得到了较好的聚类效果。对应于曲线的极值的分区用于最终估计群集的数目,并提出了新的有效性指数来量化聚类质量,独立于聚类算法和强调聚类的几何特征,有效地处理噪声数据和任意形状的聚类。
综上所述,本文对时间序列数据聚类进行了深入研究,在现有的聚类算法中,通常直接对时间序列数据进行聚类,采用欧式距离进行划分,没有时间序列对齐的灵活性,无法对时间序列数据很好地聚类。因此本文综合考虑事件的复杂结构特征,提出一种基于DTW与K-medoids算法相结合的学习模型,通过引入时间动态规整,提高聚类对动态时间序列对齐的灵活性,使聚类适用于动态时间序列数据,同时构建阈值机制实现对工业数据的监督和预警。
1 K-medoids算法理论
传统K-medoids聚类算法使用一个代价函数来评估聚类质量的好坏,以重复迭代的方式寻找到最好的聚簇划分及聚簇中心点。这里使用基于欧式距离的聚类误差平方E来评估聚类结果质量,定义如下:
(1)
式中,x为各个簇类Cj中的样本;Oj为其聚类中心。
K-medoids聚类算法步骤可描述如下:
步骤1:从数据集中随机选择k个对象,作为初始的聚类中心点;
步骤2:根据与中心点距离的远近,将数据集中的其他非中心点对象分配到最近中心点所在的簇类;
步骤3:重新计算每个簇的中心点位置,使其到该簇其他样本的距离总和最小;
步骤4:重复执行步骤2和步骤3,直到聚类误差平方和基本不变,达到指定要求为止。
一般K-means聚类算法是通过计算簇类点的平均值来选取中心点,其对孤立点敏感,选取的中心可能不存在。与K-means聚类算法不同的是,K-medoids聚类算法在迭代选取中心点时,总是在中心点的周围选择样本点作为新的中心点,消除了对孤立点的敏感性。
2 DTW-kmedoids聚类算法及阈值模型
DTW-kmedoids聚类算法是K-medoids算法结合DTW的改进。该算法利用了DTW距离可以反映样本相似性的特性,以DTW距离为基础构建了聚类结果质量的代价函数。
2.1 DTW算法
DTW最早由日本学者Itakura提出,是一种基于动态规划(DP)思想的动态时间归整算法。DTW可以实现不等长时间序列的度量,还对时间序列的偏移、振幅变化等情况具有较强的鲁棒性[17]。ROHIT等[18]指出,DTW特征与其他机器学习方法的结合使用,可以提高机器学习方法的性能。
DTW的计算过程如下:测试模板第i帧Ti与参考模板第j帧Rj的失真度为d(i,j),设D(i,j)为测试模板匹配了i帧、参考模板匹配了j帧失真度。为了求取最终答案DTW(m,n),可以定义1个矩阵,矩阵的(i,j)位置包含d(i,j)和DTW(i,j)。对于规整路径W={w1,w2,w3,...,wk},有:
(2)
式中,wi的约束条件有:
(1)规整路径满足w1=(1,1),且wk=(m,n);
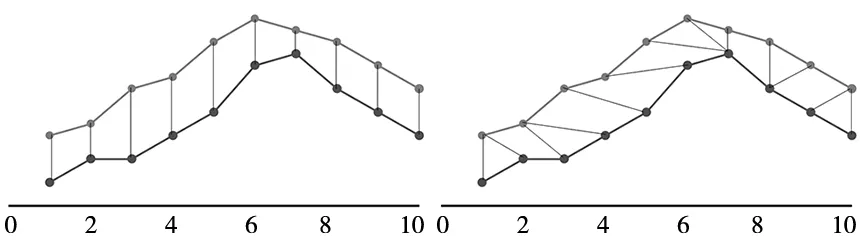
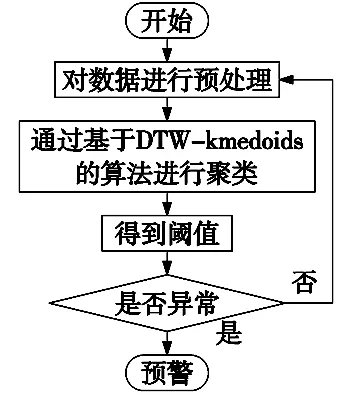
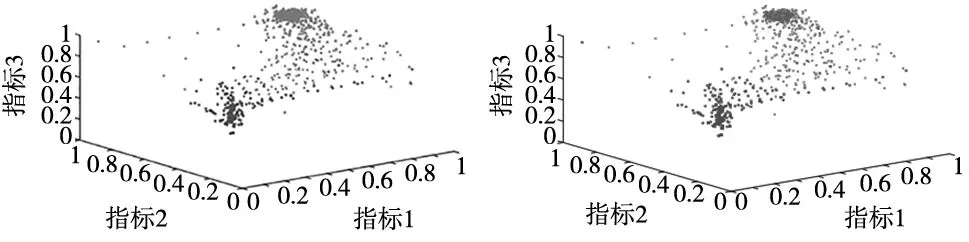
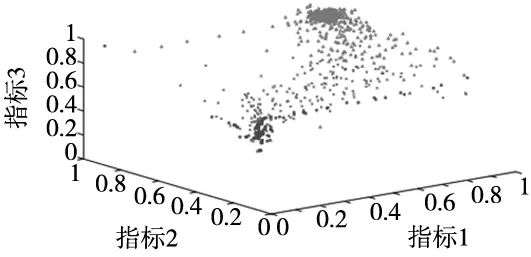
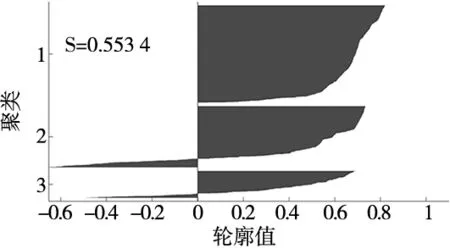
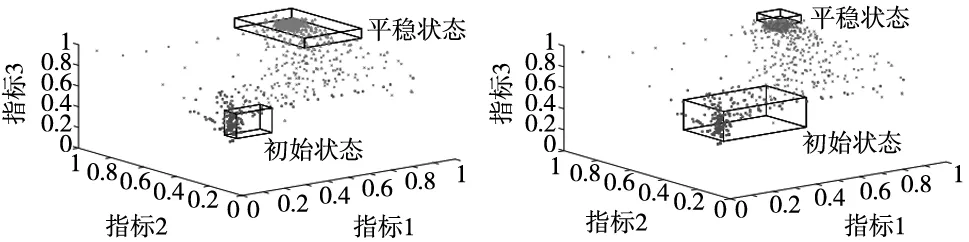
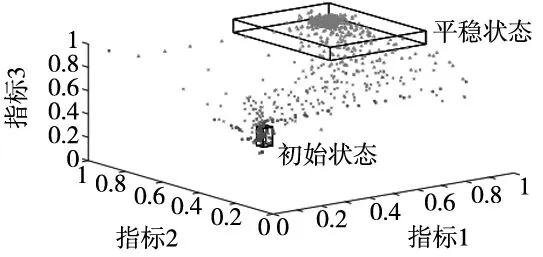
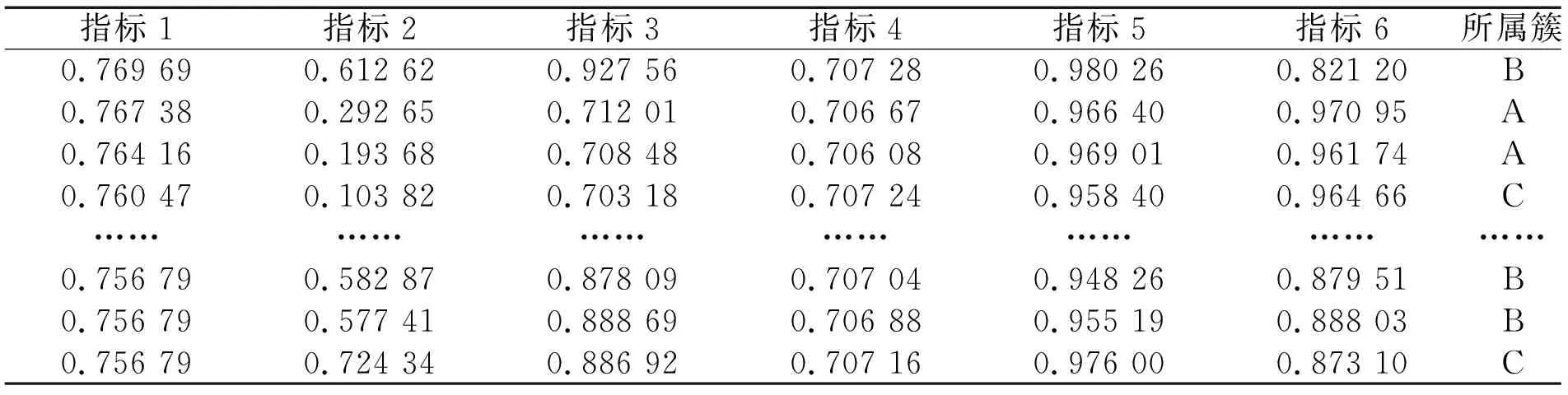
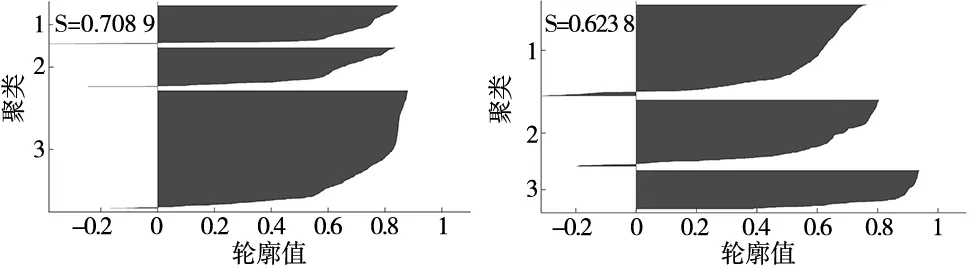
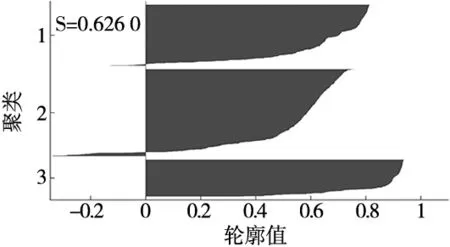
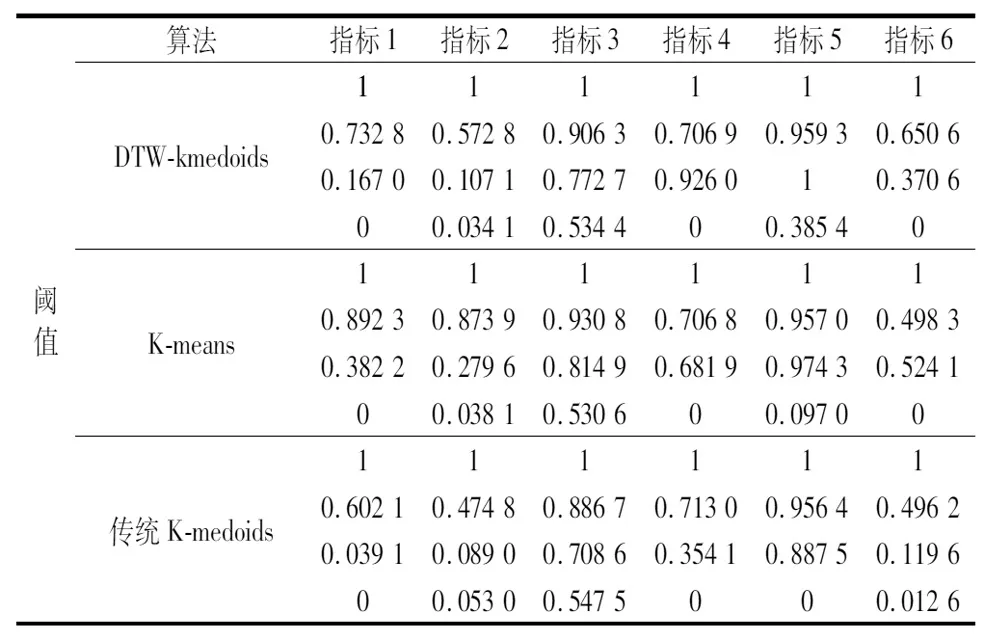
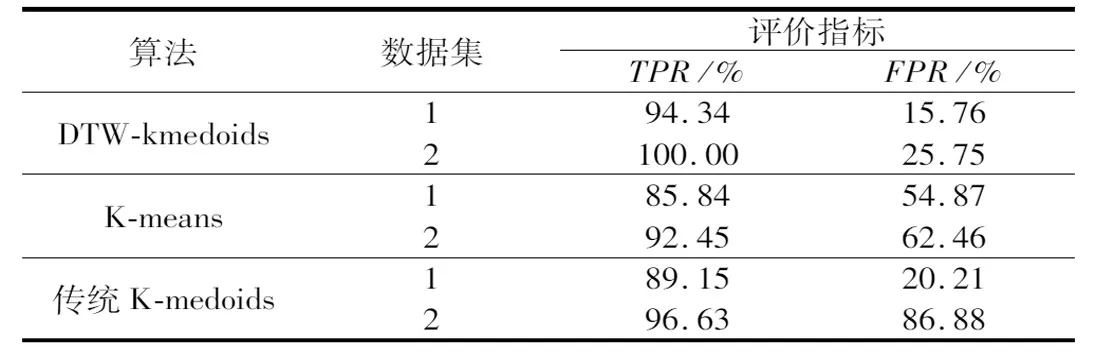
(2)对于任意的1≤i (3)对于任意的1≤i (3) 式中,DTW代表前面遍历过的区域得到的最短距离;d代表前一个坐标到该坐标的距离。 本文采用了DTW距离代替欧式距离,形成了一种新的基于DTW的对聚类结果质量的评估的代价函数,其定义如下: (4) 式中,x为各个簇类Cj中的样本;Oj为其聚类中心。 如图1所示,DTW距离的对齐方式如图1b所示,相比于欧氏距离如图1a所示,更能够体现时间序列数据特征点到对应特征点的对应关系,表现序列数据之间的相似性。DTW-kmedoids算法首先将样本标准化,然后随机选取k个样本点作为中心点并计算其他点到中心点的DTW代价函数值,根据最小的代价函数将其余的样本点归类到中心点代表的簇,重新计算中心点的位置,对其他样本点归类,并计算新的中心点的代价函数,留下代价值最小的中心点,重复这个过程,直到代价函数值达到最小。它的具体算法如表1所示。 (a) 欧式距离对齐 (b) DTW距离对齐图1 欧氏距离和DTW距离的对齐模式 表1 DTW-kmedoids算法 阈值通过以下方法设定:将每个簇的中心设为Centeri(i=1,2,3),簇边界设置于到中心的平均距离,阈值则确定于两个簇的边界之间,对于每一个数据维度,有上下两个阈值: Hthreshold= (5) Lthreshold= (6) 式中,ni(i=1,2,3)代表每个簇内样本数据量;aj代表样本经过预处理后的值。阈值可以用来确定正常数据的范围,剩下的就是异常数据。 在聚类算法的评价中,引入了评价指标轮廓系数。它的计算公式为: (7) 式中,ai为样本i到同簇其他样本的平均距离。所有样本的轮廓系数的平均值称为聚类结果的平均轮廓系数,是该聚类是否合理、有效的度量。当平均轮廓系数接近1时,簇内紧凑,并远离其他簇。 除了聚类评价指标轮廓系数,本文还引入了机器学习评价指标检测成功率TPR和误报率FPR。 (8) (9) 式中,TP代表真正类,即样本的真实状态是异常状态,而且模型预测的结果也是异常状态;FP代表假正类,即样本的真实状态是正常状态,而且模型预测的结果是异常状态;TN代表真负类,即样本的真实状态是正常状态,而且模型预测结果也是正常状态;FN代表假负类,即样本的真实状态是异常状态,而且模型预测的结果正常状态。TPR越高,说明有越多的异常样本被模型预测正确,模型的效果越好;FPR越低,说明有越少的正常样本被识别为异常样本,模型的效果越好。 基于DTW-kmedoids算法,本文构建了对时间序列数据的异常检测模型,如图2所示。首先对数据进行预处理,使数据归一化;利用DTW-kmedoids对数据进行聚类,得到聚类结果;对于聚类后的样本,使用式(5)、式(6)的阈值进行判定,大于Hthreshold或小于Lthreshold的判定为异常值。 图2 基于DTW-kmedoids的异常检测模型 实验对象选择的是贵阳市某卷烟厂1个月内31个批次烟叶加工过程中含水率的时间序列数据。烟叶含水率对烟叶后续加工质量有着非常大的影响,烟叶含水率不足,会降低烟叶的耐加工性能,增加后续加工中的损耗。本文使用的是不同工艺后烟叶的含水率数据,因为生产工艺在理论上有先后的顺序,因此将生产工艺数据看作时间序列数据。基于DTW的改进K-medoids算法对具有时间序列的含水率数据进行聚类和异常识别,为监管者提供了良好的理论支持,数据指标和数据如表2和表3所示。 表2 时间序列含水率指标 表3 时间序列含水率数据 表2反映了本次实验6个输入指标,以及聚类评价指标轮廓系数、异常检测的检测成功率和误报率这两个指标。 因为时间序列数据中有三种含水率状态:初始状态,异常状态,平稳状态,所以本文设k=3。用聚类算法可以得到对应的三类。采用了K-means算法,经典K-medoids算法和DTW-kmedoids算法对以上数据进行聚类。在聚类结果中,按比例缩放后,初始状态样本点与其自身质心之间的所有距离都小于0.1,但它们与另外两个状态质心的距离相对较大,即4.5~9.0。相反,处于平稳状态中所有样本与初始状态质心之间的距离大于7.5,而到它们自己聚类中心的距离都小于0.12,这表明,处于初始状态、异常状态和平稳运行状态的样本明显分布在三个不同的区域。三种图案的样本可以清晰地相互区分,为阈值区分奠定了基础。 在上述6个指标中选取了3个,首先对数据进行了可视化处理,如图3所示。 图3 时间序列含水率分布 为了验证基于DTW-kmedoids的烟丝含水率控制模型的有效性和准确性,选取了1043个样本,其中包括314个初始状态样本,212个异常状态样本,517个平稳状态样本。本次实验选取了指标1、指标2、指标3三个输入指标,以及聚类评价指标轮廓系数、异常检测的检测成功率和误报率这两个指标。首先分别采用了K-means算法,经典K-medoids算法和DTW-kmedoids算法进行聚类,根据聚类效果建立对应的阈值对数据进行划分,如果样本不属于初始状态,也不属于平稳状态,则相应的测试样本被视需要控制的样本;否则,它将被视为正常样本。聚类结果如图4所示。 (a) DTW-kmedoids聚类结果 (b) K-means聚类结果 (c) 传统K-medoids聚类结果图4 聚类结果 图4可以明显看到烟丝含水率数据聚集于初始状态和平稳状态,而中间较为离散的数据正处于异常状态。根据图4aDTW-kmedoids算法的聚类结果,可以看到这些数据清晰地聚为3类。图4b中K-means算法将一部分平稳状态样本识别为异常样本,这是因为异常状态的均值中心偏离,导致相似度较高的样本被不同的中心点俘获。图4c中传统K-medoids算法区分出了平稳状态,但是未能根据时间相似性区分初始状态和异常状态,导致某时间段内样本被分为两部分。 对聚类样本求轮廓系数,结果如图5所示。 (a) DTW-kmedoids轮廓系数 (b) K-means轮廓系数 (c) 传统K-medoids轮廓系数图5 轮廓系数 图5a为DTW-kmedoids聚类结果的轮廓系数图,正数较多,平均值更接近1;图5b和图5c分别为K-means和传统K-medois算法聚类结果轮廓系数图,负数相对较多,平均值较小。可得本文提出的DTW-kmedoids算法相对于K-means算法和传统K-medoids算法比较有较明显提升。这说明,DTW-kmedoids算法能在增大类间距离的同时,有效地减小类内距离。 根据式(5)、式(6),得到的阈值模型如图6所示。 (a) DTW-kmedoids获得的阈值 (b) K-means获得的阈值 (c) 传统K-medoids获得的阈值图6 不同聚类算法获得的阈值 图6中,对于初始状态的3个指标,各有两个阈值进行识别,6个阈值代表的面围成了长方体,长方体内部的数据代表识别为初始状态;平稳状态亦然。得益于DTW-kmedoids算法优秀的聚类效果,图6a中的阈值可以很好地识别出数据的初始状态和平稳状态,而剩下的就是异常数据。图6b中代表平稳状态阈值的长方体较小,导致K-means算法异常识别误报率较高。图6c中传统K-medoids算法未能准确区分初始状态和异常状态,导致初始状态阈值长方体偏离初始状态数据簇类,进而使识别准确率不足。 除了上述实验,本文还使用了全部指标进行了实验Ⅱ,表4~表6是实验Ⅱ的聚类结果,A为平稳状态,B为异常状态,C为初始状态。 表4 DTW-kmedoids聚类结果 表5 K-means聚类结果 表6 传统K-medoids聚类结果 对实验Ⅱ聚类样本求轮廓系数,结果如图7所示。 (a) 六维数据DTW-kmedoids轮廓系数 (b) 六维数据K-means轮廓系数 (c) 六维数据K-medoids轮廓系数图7 实验Ⅱ得到的轮廓系数 图7a为DTW-kmedoids聚类结果的轮廓系数图,图7b和图7c分别为K-means和传统K-medoids算法聚类结果轮廓系数图。依然可以看出本文提出的DTW-kmedoids算法相对于K-means算法和传统K-medoids算法比较有较明显提升。再次说明,DTW-kmedoids算法能在增大类间距离的同时,有效地减小类内距离。上述两个实验均能表明,基于DTW-kmedoids算法可以对时间序列数据有效地进行聚类。表7是实验Ⅱ得到的阈值。 表7 不同算法得到的阈值 结合这两个实验,得到了异常识别准确率的对比,结果如表8所示。 表8 异常识别准确率对比 根据表8,基于DTW-kmedoids算法的模型识别率可以达到最高,误报率最低。3种方法表明,基于DTW-kmedoids算法得到的阈值效果最优,对异常值的判断最为准确,进而说明了该方法能够在克服烟丝加工工艺对湿度影响的前提下提取和区分烟丝特征。因此,基于DTW-kmedoids算法的模型足以识别异常样本。在异常样本出现时,可以及时调整生产工艺,减少异常,降低烟叶含水率不足对后续加工的影响。 本文针对现有基于聚类算法的时序数据异常检测进行了分析和研究,提出了一种基于改进K-medoids算法(DTW-kmedoids)的时间序列数据异常检测模型。以卷烟厂的时序数据为实验对象,通过对具有时间序列特性的烟丝含水率数据进行聚类分析,并以K-means算法、传统K-medoids算法为参照进行了实验对比。结果表明,本文提出的基于DTW-kmedoids的模型在跟踪与监督烟丝含水率异常检测方面更具有优势,能有效完成工业生产中对时间序列数据的监督,并能够提高时间序列异常数据检测的有效性和精确性,进而为工厂管理者提供理论技术支持。
2.2 DTW-kmedoids算法

2.3 阈值的确定
2.4 评价指标
2.5 模型流程
3 实例验证
3.1 实验数据及参数

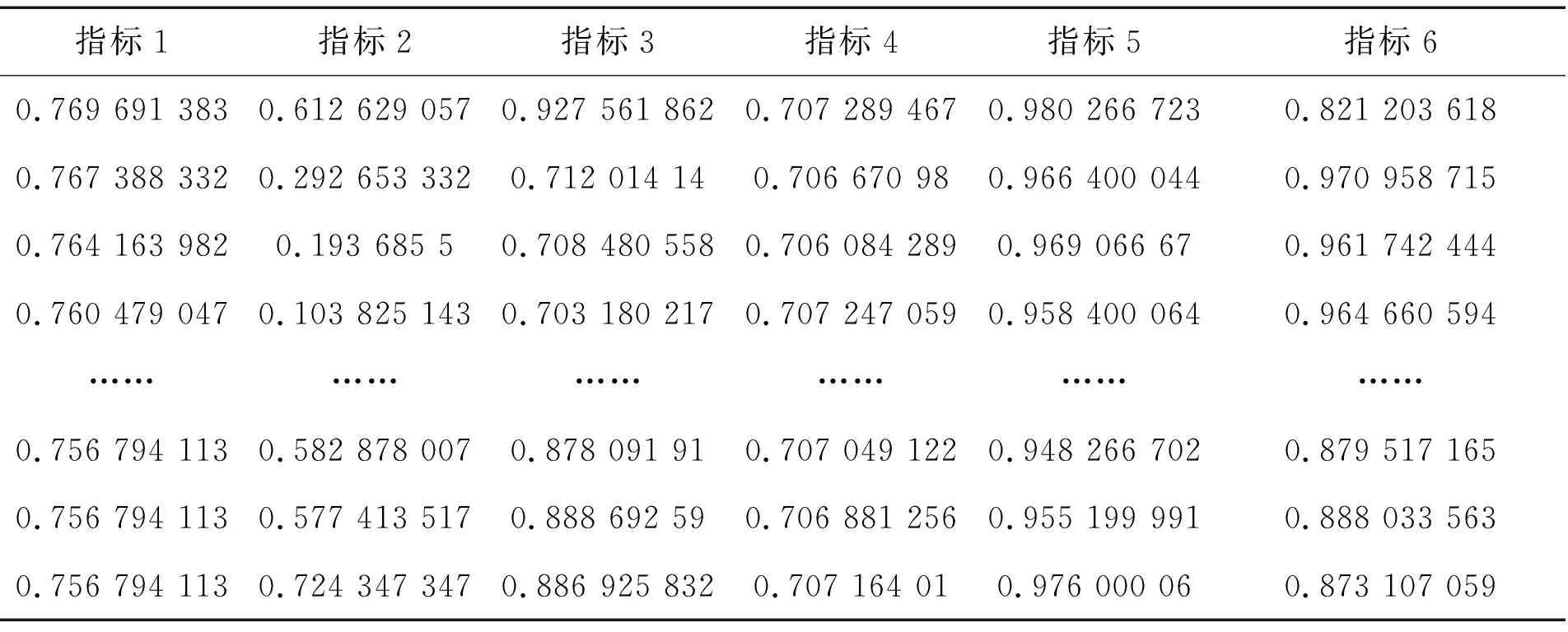
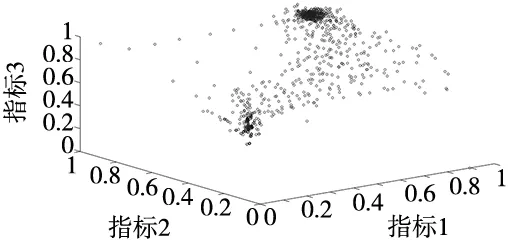
3.2 实验结果



4 结论

