基于时移多尺度注意熵和随机森林的水电机组故障诊断

陈 飞，王 斌，刘 婷，张文静，高园晨，陈帝伊

（西北农林科技大学 水利与工程建筑学院，陕西 杨凌 712100）

1 研究背景

水电机组作为水电站的核心部件，维护机组安全稳定对电站高效运行有着很大的现实价值。振动信号作为水电机组运行状态的外在表现形式，常被用作评价水电机组健康状态的重要指标。振动是引发机组故障的主要原因，据统计，由于振动导致的故障占到机组总故障的80%［1］。因此，利用振动信号进行水电机组故障识别是常用的诊断方法。

机组常常在高噪声环境下工作，故障信号容易受到噪声干扰，为机组故障识别增加了难度。因此，如何在噪声环境下提取有效故障信息，成为了机组故障诊断的关键。文献中常利用奇异值分解（Singular value decomposition，SVD）［2］、变分模态分解（Variational mode decomposition，VMD）［3］以及自适应局部迭代滤波（Adaptive local iterative filtering，ALIF）［4］等方法对信号进行降噪，从而实现故障特征有效提取。但是，以上方法降噪过程中不可避免会导致一部分有效故障信息丢失。因此，直接提取信号故障信息需要一种抗噪性能良好的特征提取工具。熵作为度量时序信号复杂性的重要工具，在水电机组特征提取领域有着广泛的运用［5-8］。文献［6］将样本熵和时频域指标相结合形成多维特征，有效区分出机组不同故障类别。然而，样本熵在处理长时间序列时，需要消耗较长时间［9］。相比于样本熵，排列熵计算更为简单和快速［10］。何洋洋等［11］提出一种基于随机共振和多维度排列熵的水电机组故障诊断模型，有效提取机组故障信息。但是，排列熵忽略了信号振幅之间的差异，从而导致有效信息的丢失［12］。为了克服以上熵的不足，Yang 等［13］提出了一种新的度量信号复杂性工具——注意熵。不同于传统熵关注时间序列中所有数据的频率分布，注意熵只注重于序列峰值点间隔的频率分布情况。因此，注意熵具有超参数少、运行时间短、对时间序列长度鲁棒性强等优点。针对注意熵无法在多个尺度综合衡量时序信号复杂性，本文将注意熵和多尺度熵相结合，提出了多尺度注意熵（Multiscale attention entropy，MATE）。同时，针对传统多尺度熵粗粒化不足的问题，受文献［14］中时移方法思想启发，提出了一种度量信号复杂度的工具——时移多尺度注意熵（Time-shifted multiscale attention entropy，TSMATE）。通过仿真实验验证，TSMATE 具有良好的抗噪性能，可以有效提取水电机组故障信息。

水电机组故障诊断的实质是模式识别。将特征信息输入到分类器中，利用分类器区分不同故障信号。近些年，随着人工智能的不断发展，机器学习、深度学习等一系列模型被应用于水电机组模型建立［15］、振动趋势预测［16］以及机组状态监测［17］等领域。文献［18-20］利用卷积神经网络、概率神经网络以及支持向量机等算法充当分类器，实现了机组不同故障状态的准确识别。但是，存在超参数难以调节、计算复杂度高等问题，阻碍了这些算法在机组故障诊断方面的进一步运用。随机森林（Random forests，RF）作为集成学习的一种，不仅有精度和效率高的特点，还具备参数可解释性强、变量敏感度分析等优势。在轴承故障诊断［21］、地理遥感［22］、作物生长［23］以及风速预测［24］等方面都有着广泛的应用。本文引入RF 算法作为分类器，完成对机组不同故障信号识别。仿真实验表明，RF可以高效识别不同状态信号。

针对传统方法难以准确识别高噪声下不同状态的故障信号，本文提出了一种基于TSMATE 和RF 相结合的水电机组故障诊断模型。首先，受时移思想启发，提出了一种衡量时间复杂度的工具——TSMATE。通过分析不同信噪比噪声下机组振动信号的特征分布情况，验证了TSMATE 具有良好的抗噪性能。然后，针对特征冗杂问题，本文引入主成分分析（Principal component analysis，PCA）进行降维处理，提高了模型运行效率。最后，将降维后的低维特征输入到RF中，实现了水电机组故障的精确诊断。

2 TSMATE-PCA-RF 故障诊断模型建立

2.1 注意熵 Yang 等［13］通过关注时间序列中关键点变化情况，提出了一种新的度量时序复杂度工具——注意熵。对比传统熵，注意熵具有对时序长度鲁棒性强、无需设置超参数等优点，如图1 所示，计算时序注意熵可概括为以下几步：

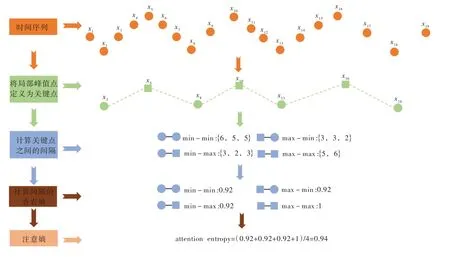
图1 注意熵示意图

（1）如果时间序列中的每一个点都被认为是一个系统，其状态的变化就可以看作是系统对环境的调整。峰值点可以有效表征局部状态的上下界变化情况，因此将局部峰值点定义为关键点。

（2）按照{min-min}、{min-max}、{max-min}以及{max-max}4 种不同策略设定为关键点，并计算相邻关键点的间隔点数。

（3）计算相邻关键点间隔香农熵，具体公式见式（1）：

式中：p( x )为x 发生的概率；b 为间隔点种类个数。

（4）将4 种不同策略计算得到的香农熵均值定义为注意熵。

2.2 时移多尺度注意熵（TSMATE） 注意熵仅在单一尺度衡量时序复杂度，难以全面反映出信号的有效信息。针对这个问题，Costa 等［25］提出多尺度熵概念，通过对时序信号进行分割，实现了多尺度度量信号复杂度的目的。本文将多尺度熵和注意熵相结合，并基于分形理论，提出了TSMATE，克服了传统多尺度熵粗粒化程度不足以及参数难以调节等问题。TSMATE 具体计算过程如下：

（1）通过式（2）将长度为N 的时序信号分割成k 个子序列。

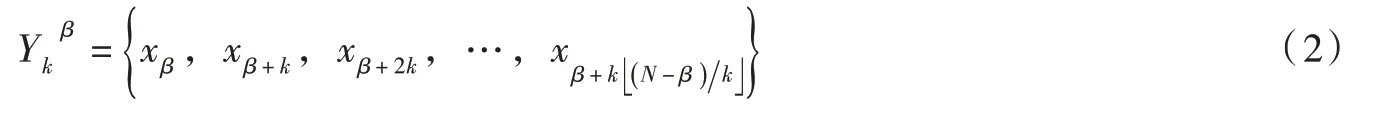
式中：x 为原始信号的样本点；k 为分割子序列的个数；Ykβ为第β个子序列。

（2）计算所有尺度时序信号的注意熵，并将这些注意熵的均值定义为该尺度k 下的

式中ATE( Ykβ)为Ykβ的注意熵。

（3）利用式（3）计算所有k 的TSMA（k），将这些值的集合作为TSMATE。

2.3 主成分分析（PCA） 本文将振动信号的TSMATE 作为特征向量。同时，利用PCA 降维技术克服TSMATE 特征冗杂问题。通过将高度相关特征变量转化为相互独立的低维变量，降低数据的复杂度，提高模型的训练效率。PCA 的步骤如下：

（1）将输入数据样本转化成标准化矩阵。

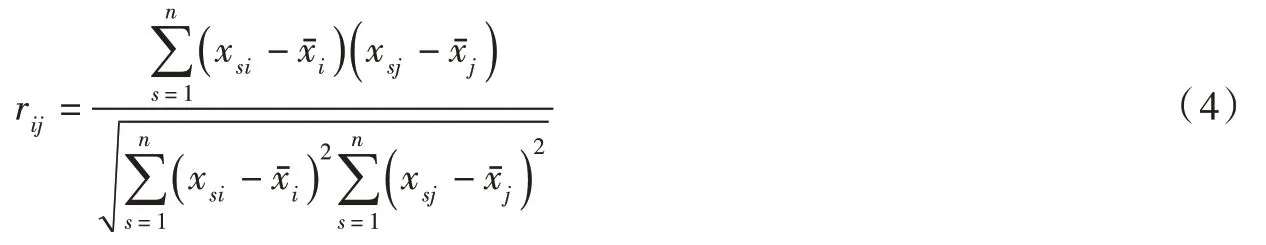
式 中：rij为变量xi和变量xj的相关系数；n 为样本数；m 为特征数；为 第i 个变量的均值；为 第j 个变量的均值；xsi为第s 个样本中i 变量的值；xsj为第s 个样本中j 变量的值。

（3）计算相关系数矩阵G 的特征方程，得到矩阵的特征值λ和对应特征向量。

（4）通过式（5）和式（6）计算贡献率κi和累计贡献率ηi

（5）根据步骤4，选取PCA 的特征值和特征向量，最终得到降维后的数据。

2.4 随机森林（RF） 将降维特征输入到分类器中，利用分类器有效区分不同故障信号。RF 是一种基于Bootstrap 取样与Bagging 投票的方法。同时，作为集成学习的一种算法，是一个包含多个决策树的多分类器，并且其输出的类别是由决策树输出的类别的众数而定。

Bootstrap 取样方法是一种有放回的抽样方法，故可以得到容量与被抽样样本相同的样本。假设样本容量为无穷大时，约有36.8%的袋外样本不可以被抽中，这部分数据通常用来检测模型的泛化能力。Bagging 算法是一种集成学习算法，它通过Bootstrap 取样方法进行多次取样，形成多个样本采样集，每一个采样集都可训练成一个弱学习器，各个弱学习器相互独立，分别对数据进行处理并投票，票数最多的便是算法的结果。RF 是一种改进的Bagging 算法，它采用CART 决策树作为弱学习器，故各个决策树相互独立，只能保留原始样本的部分数据特征。

RF 的构建由以下三个部分组成：

（1）RF 每一轮训练样本数据时，采用有放回的抽样方法从样本数据中抽取P 个样本，并据此构建P 个决策树。

（2）随机选择决策树的训练数据，假设样本有M 个特征属性，从M 个特征属性中随机选择l 个特征属性，作为决策树的训练属性。

（3）生成的P 个决策树组成一个RF，由每个决策树共同决定分类结果。

水电机组故障诊断总体流程如图2 所示，将振动信号的TSMATE 作为特征向量。针对特征冗杂问题，本文利用PCA对特征向量进行降维处理。最终将降维数据输入到RF模型中，利用RF进行故障识别。

图2 水电机组故障诊断流程图

3 仿真实验

3.1 TSMATE 稳定性分析 为验证TSMATE 的合理性，本文分析了Blue noise、Violet noise、Pink noise 以及Red noise4 种不同的1/f 噪声（见图3）下TSMATE 随信号长度变化情况。

图3 1/f 噪音信号

如图4 所示，对比TSMATE 和MATE 在4 种不同噪声上的分布情况，发现随着时序信号长度的减小，MATE 波动逐渐增大，尤其在一些尺度上MATE 值发生了突变。以时序长度N=1000 的噪声信号为例，不同噪声的MATE 分布在尺度因子大于16 时，MATE 值变化剧烈。同时，不同长度噪声信号MATE 的分布差异过大，4 种噪声的MATE 波动最大幅值分别达到了0.485、0.443、0.491 以及0.604，说明传统的粗粒化方法不能有效分割短序列信号。

图4 TSMATE 和MATE 分 布情况

对比MATE，论文所提的TSMATE 在4 种噪声的波动最大幅值为0.137、0.158、0.187 以及0.386，说明TSMATE 在不同的时序长度上分布基本一致。并且，随着尺度因子的增大，TSMATE 值逐渐趋于平稳，表明TSMATE 对时间长度具有良好的鲁棒性。

3.2 数据收集 文献［26］利用转子故障试验台，模拟水电机组正常、碰摩、不平衡以及不对中4 种不同类别的振动信号。其中，振动信号的采集频率为2048 Hz，共采集到360 个振动信号。如图5 所示，通过对振动信号加入0 dB、1 dB、2 dB 以及3 dB 4 种不同信噪比的噪声，探究不同噪声下TSMATE 的特征提取性能。

图5 不同噪声的振动信号

3.3 TSMATE 特征提取 为探究TSMATE 在不同噪声下的特征提取能力，引入多尺度熵（Multiscale entropy，MSE）以及时移多尺度熵（Time-shifted multiscale entropy，TSMSE）进行对比实验。图6 清晰表明采用时移思想得到的多尺度熵相较于传统多尺度熵更为稳定，说明了时移思想可以有效克服传统多尺度熵粗粒化不足的问题。图7 分析了机组信号在无噪声下不同熵的分布情况，同时利用T-分布邻域嵌入（T-distributed stochastic neighbor embedding，T-SNE）将不同机组状态信号的特征三维可视化。从图中可以看出，TSMATE 有效地将各类故障信号区分，其它3 种熵都有着不同程度的混叠。其中，采用MATE 和MSE 提取的特征中正常信号、碰摩信号以及不对中信号有少量混叠，而采用TSMSE 提取的特征中碰摩信号和不对中信号也有着少量混叠。以上现象说明，TSMATE 在无噪声下具有良好的特征提取性能。为进一步分析TSMATE在噪声下的特征提取情况，这里对振动信号加入0 dB、1 dB、2 dB 以及3 dB 4 种不同强度的噪声。

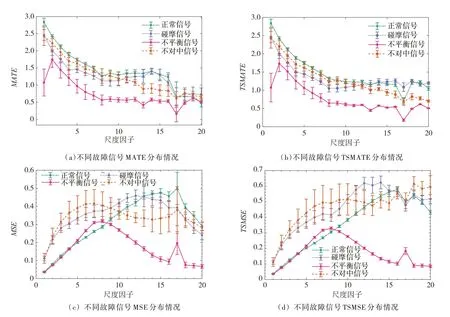
图6 机组信号不同熵分布情况（无噪声）

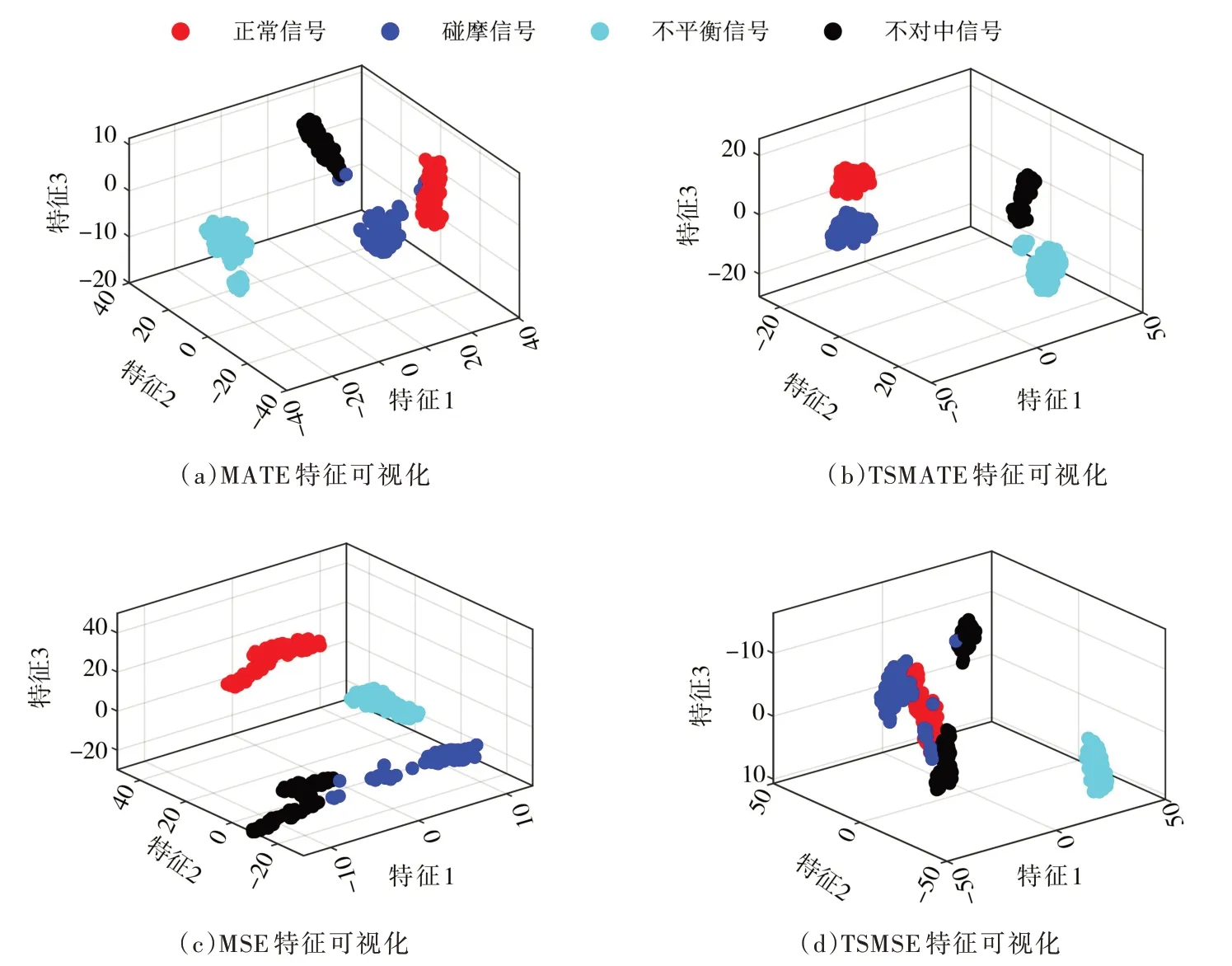
图7 机组信号不同熵特征可视化（无噪声）

限于篇幅，本文只分析了0 dB 强噪声下机组振动信号的不同多尺度熵分布情况。如图8 所示，相较于MATE 等多尺度熵，TSMATE 表现出良好的稳定性，在各种状态振动信号中TSMATE 熵值基本保持一个稳定状态，说明了TSMATE 是一种稳定的特征提取工具。

图8 机组信号不同熵分布情况（SNR=0 dB）

图9 分析在0 dB 噪声干扰下，不同多尺度熵的T-SNE 可视化结果，发现MATE 中正常信号和碰摩信号发生了混叠，不平衡信号和不对中信号也有少量的混杂现象发生。MSE 中碰摩信号和不对中信号完全混杂在一起，正常信号和碰摩信号也有零星混叠。同样，TSMSE 碰摩、不对中、不平衡以及正常信号也存在混杂现象。对比以上3 种多尺度熵，TSMATE 仅有个别碰摩信号与正常信号存在混杂。

图9 机组信号不同熵特征可视化（SNR=0 dB）

图10展示了不同噪声下TSMATE特征提取情况，发现随着噪声的增加，不同状态信号特征混叠现象不断加重。分析不同噪声下特征的三维可视化图，可以清晰地看出不对中信号和不平衡信号被有效区分，而正常信号和碰摩信号特征则发生了混杂，说明噪声在一定程度上降低了TSMATE 的特征提取效果。总体上看，TSMATE对噪声具有良好的适应性，在高噪声下TSMATE也可以提取较好的特征数据。

图10 不同噪声下TSMATE 特征三维可视化

另外，为探究所提方法的运行效率，比较了TSMATE、MATE、TSMSE 以及MSE 特征提取时间。从表1 中可以看出，TSMATE 和MATE 相对于未改进的多尺度熵只需要耗费更短的时间。MATE 提取机组振动信号特征仅需要10 s，本文所提的TSMATE 也只需要45 s 左右，远远低于TSMSE 和MSE。通过上述内容分析，说明了论文所提算法是一种高效稳定的特征提取工具。

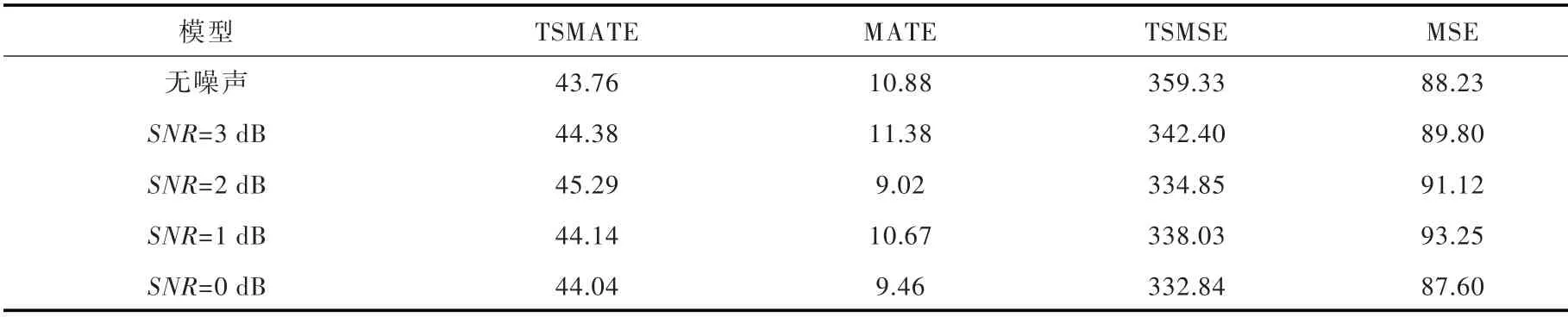
表1 不同熵提取特征时间 （单位：s）

3.4 RF 故障识别 针对特征向量冗杂问题，采用PCA 对4 种不同的熵进行降维处理。将降维后的低维特征输入到RF 模型中，实现对机组不同故障信号的有效识别。其中，RF 决策树数目设置为100，每个决策数的特征属性个数定为5。

为验证模型的泛化性能，可以通过十折交叉法划分训练集和测试集进行测试。如表2 所示，通过对比不同模型的诊断效果，发现PCA-TSMATE-RF 模型在所有数据集中都取得了98%以上的诊断精度，在所有模型中排名第一。从表2 可以看出在SNR=0 dB 时，MSE 和TSMSE 等传统多尺度熵最高诊断率为92.78%，而所提方法的诊断率为98.06%，比传统多尺度熵高5.28%。同时，为分析不同诊断模型在强噪声（SNR=0 dB）下具体诊断情况，本文选取了MATE-RF、TSMATE-RF、PCA-MATE-RF以及PCA-TSMATE-RF 4 种诊断模型进行对比，具体情况见图11，从图中看出，PCA-TESMATE-RF模型在识别正常信号和碰摩信号时发生了一定偏差，这与上节的特征可视化结果相吻合，也说明了噪声会在一定程度上干扰诊断。通过以上分析，验证了本文所提方法的高效性和精准性。

表2 不同模型的诊断精度

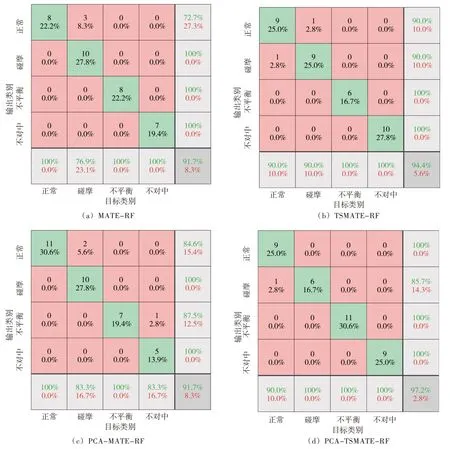
图11 不同模型诊断率（SNR=0 dB）

4 结论

针对高噪声对水电机组故障诊断的干扰，提出了一种基于TSMATE 和RF 相结合的水电机组故障诊断方法。通过分析仿真实验，得到以下结论：

（1）针对MATE 粗粒化不足，将时移思想引入MATE 中，提出TSMATE。对比不同长度的Blue noise、Violet noise、Pink noise 以及Red noise 下TSMATE 和MATE 分布情况，发现TSMATE 基本不受时间长度的影响，验证了TSMATE 对短时序信号具有良好的鲁棒性。

（2）对比不同多尺度熵的特征分布情况，发现TSMATE 提取的特征最为稳定。同时，通过T-SNE三维可视化分析不同多尺度熵特征提取情况，发现不同噪声干扰下，TSMATE 只有少量的碰摩信号和正常信号发生了混叠。仿真结果表明，TSMATE 具有良好的抗噪性能。

（3）为验证模型的泛化性能，采用十折交叉法划分训练集和测试集进行测试。TSMATE-PCA-RF等8 个模型在不同信噪比振动信号的诊断精度对比表明，所提模型在不同强度噪声下都可以取得最好的诊断效果。例如，在强噪声（SNR=0 dB）的干扰下，所提方法比传统多尺度熵高5.28%，同时，采用TSMATE 模型均取得了96%的诊断率。

实验结果表明，本文所提的水电机组诊断方法可以精准识别高噪声环境下不同故障信号，为水电机组故障诊断提供了新手段。