基于噪声水平的感应式磁传感器最优化设计

杜政 陈兴朋 席振铢 唐尧

摘要：感应式磁传感器是地球物理勘探中最常用仪器之一，噪声水平是感应式磁传感器的核心技术指标。长期以来，感应式磁传感器的设计人员饱受其研发周期长、设计效率低的困扰，需要优化设计方法来缩短周期，提高效率。首先理论分析感应式磁传感器噪声在不同频段的分布规律，给定感应式磁传感器的设计要求后，构建噪声和磁芯长径比、磁导率的函数关系，得到满足设计要求的最优磁芯质量;随后定义一个质量因子，构建噪声与质量因子的函数关系，计算线圈质量，进而得到绕线的最佳直径，并在感应式磁传感器绕组比确定的情况下，计算得到线圈匝数;最后利用上述方法设计并制作1个1～100 000 Hz感应式磁传感器，测得其噪声水平在频率范围内均满足设计要求，证明此最优化设计的合理性。

关键词：感应式磁传感器;噪声水平;最优化设计;质量因子;实物测量

中图分类号：TD178文献标志码：A

文章编号：1001-1277（2022）05-0056-07doi：10.11792/hj20220511

引 言

感應式磁传感器（Induction or search-coil Magnetometers，IM）具有频率范围广、物理结构简单、成本低等优点，是大地电磁测深法中应用最广泛的传感器[1]。感应式磁传感器研制起步于20世纪60年代，经过半个多世纪的发展，加拿大凤凰公司的AMTC系列传感器、德国Metronix公司的MFS系列传感器、美国Zonge公司的ANT系列传感器均处于世界领先地位[2]。20世纪80年代，原航空工业部国营延光机械厂自主研发了CGY-1A型感应式磁传感器;21世纪初，西安庆安航空电器公司研制了MC-01传感器。中国地质科学院地球物理地球化学勘查研究所的IGGE-30/80系列感应式磁传感器[3]，中国科学院电子学研究所与中国科学院地质与地球物理研究所研制的CAS系列感应式磁传感器，以及湖南省五维地质科技有限公司的ICMS-H自研高频磁传感器[4]均具有较高水平。

噪声是感应式磁传感器设计过程中一项重要的技术参数，主要受磁芯和线圈2个部分影响，一般来说，磁芯的磁导率越高、长径比越大、绕线匝数越多，则感应式磁传感器的灵敏度越高，噪声水平随之降低[5]。但考虑到施工的便携性和传感器的耐用性、易于维护等需求，过长或者横截面积过大、绕线匝数过多的感应式磁传感器均不符合实际需求。另外，感应式磁传感器的研制是设计、制作及测试等反复试制的过程，因而造成感应式磁传感器研发周期长、效率低。总之，为了高效制作低噪声、宽频带并且轻便的感应式磁传感器，亟需最优化设计方法。本文通过理论分析，根据给定的感应式磁传感器设计要求，经过数值建模与计算、图像分析，结合实际工程经验，得出一套感应式磁传感器最优化设计技术，极大缩短了感应式磁传感器的设计周期，提高了设计效率。

1 感应式磁传感器的噪声分布规律

地磁场信号主要分布在10-4～106 Hz频段，在频率0.000 1～1 000 Hz呈衰减趋势，强度从1 000.00 nT降低到0.01 nT以下，衰减幅度大于5个数量级;当频率在0.5，3，1 000 Hz附近时，地磁场信号强度存在极小值[6];频率在3～30 Hz时，由于舒曼共振的存在，地磁场信号强度有所增加。除了上述极值点，地磁场信号强度在频率范围内还存在5处波峰，3处波谷;当频率大于1 000 Hz时，地磁场信号强度呈现缓慢上升趋势，如图1所示[7-9]。在研制过程中，需要严格控制感应式磁传感器的噪声水平，使得噪声强度在全频段范围内均低于地磁场信号强度，从而能够接收到来自地磁场的有效信号[10-20]。

噪声与感应式磁传感器的组成部件密切相关，感应式磁传感器由1根长条形高磁导率磁芯缠绕数万乃至数十万匝的线圈构成（如图2所示），变化的地磁场在线圈中产生感应电压，经感应线圈接收，前置放大器调理，再发送到主机，从而对感应电压进行处理与分析（如图3所示）。在提取地磁场信号的过程中，传感器会产生等效电阻热噪声（er）、前置放大器输入端的等效电压噪声（en）及前置放大器输入端的等效电流噪声（in），3种噪声源的等效电路图如图4所示。

推导计算感应式磁传感器3种噪声物理公式过程如下：

根据法拉第电磁感应定律，感应电压（V）的表达式为：

V=ndφdt=-μappnSdBdt（1）

式中：n为绕线匝数;φ为磁场强度（A/m）;t为时间（s）;μapp为磁芯的视磁导率（H/m）;S为横截面面积（mm2）;B为磁感应强度（T）;-表示感应电动势方向是沿着阻碍磁通变化方向的。

此公式在频率域内改写为：

V=-jωμappnSB（2）

式中：j为虚数单位;ω为角频率（rad/s），ω=2πf，f为感应磁场的频率（Hz）。

等效电阻热噪声（er）的表达式为：

er=4πTRΔf（3）

式中：T为开尔文温度（K）。

传感器的信号分辨率（Bt）为：

Bt2=e2rσ2f2（4）

式中：σ为电压灵敏度。

则感应线圈电阻热噪声的等效磁场噪声水平（Br）公式表达为：

Br2f=4kbTRω2μ2appn2S2（5）

式中：kb为玻尔兹曼常数，1.38×10-23J/K。

传感器电阻（R）的表达式为：

R=4ρd2wn1∑nj=1n2j[di+（n2j+1）dw]（6）

式中：ρ为电阻率（Ω·m）。

则可将式（5）改写为：

|Br|2f=16kbTρd2wω2μ2appn1n2S2[di+（n2+1）dw]（7）

前置放大器输入端电压噪声的等效磁场噪声（Bne）为：348EDD8F-EE9A-4298-8CCE-ABF94DBDD69C

|Bne|2f=|en|2f×|1+iωRC-ω2LC|2ω2μ2appn2S2（8）

式中：i为虚数单位。

同理，可得前置放大器输入端等效电流噪声的等效磁场噪声（Bni）为：

|Bni|2f=|in|2f×|R+iωL|2

ω2μ2appn2S2（9）

对于给定的前置放大电路，en和in是已知值。由此可得线圈等效磁场总噪声水平（NL）为：

NL=|Br|2f+|Bne|2f+|Bni|2f（10）

根据式（10），使用没有1/f噪声影响的物理前置放大电路电压噪声与电流噪声计算，各部分噪声对总噪声的影响规律如图5所示。从图5可以看出：当频率小于1 000 Hz时，等效电阻热噪声的影响占据主导地位;在1～10 000 Hz频段，等效电流噪声的影响最为明显;当频率大于10 000 Hz，总噪声水平主要受等效电压噪声的影响。

2 最优化设计方法

2.1 磁芯最优化设计

設计感应式磁传感器质量为2 kg，长度为700 mm，目标噪声水平为5×10-5nT/Hz @10 Hz，1×10-6 nT/Hz @1 000 Hz，1×10-5nT/Hz @10 000 Hz，从磁芯和线圈这2个模块对感应式磁传感器进行最优化设计。

磁芯是感应式磁传感器的主要组成部分，但由于磁场退磁效应的存在，磁芯的视磁导率远低于磁芯材料的相对磁导率，且严重受磁芯几何形状的影响。对磁导率的衰减规律进行数学分析，定义磁芯的长径比为w，其长度为l（mm），直径为d（mm），则w=l/d;磁芯初始磁导率为μr（H/m）。磁芯的退磁系数（Nr）只与w有关，如下所示：

Nr≈ln（2w-1）w2（11）

则改良后的视磁导率为：

μapp=μr1+Nr（μr-1）（12）

将式（10）中与磁芯物理性质无关的量定义为G，则传感器的总噪声水平可以表示为：

NL=Gw4+2（μr-1）（w2+μr-1）ln（2w-1）w4μ2r（13）

其中

G=1ω2nS216kbTρ[di+（n2+1）dw]d2w+

|en|2|1+iωRC-ω2LC|2+|in|2|R+iωL|2nf（14）

利用式（13）计算磁芯长径比的变化对感应式磁传感器总噪声水平的影响，对w求二阶导数，得到当w=40时，NL″=0。即当长径比w>40时，总噪声水平随长径比变化的速率降低，再增加长径比对改善感应式磁传感器噪声的作用降低（如图6所示）。

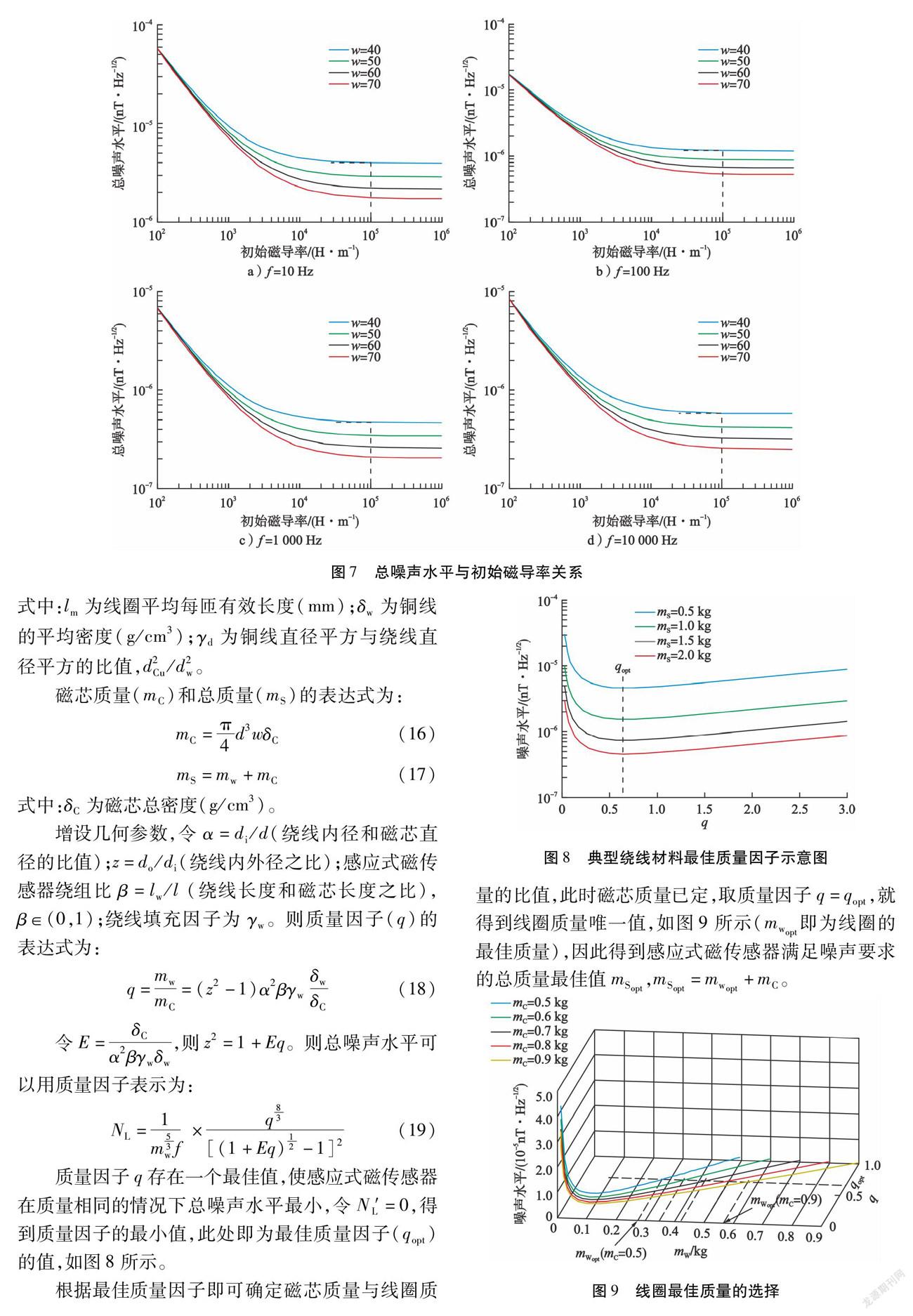
计算磁芯初始磁导率的变化对感应式磁传感器总噪声水平的影响。计算不同频率下地磁场信号强度与噪声强度的关系，对μr求一阶导数并令NL′=0，此时的磁芯初始磁导率μr>100 000 H/m，总噪声水平不随初始磁导率的降低而降低，噪声强度远小于地磁场信号强度，感应式磁传感器可以取得有效信号，计算不同频率下的总噪声水平随磁芯初始磁导率的变化情况，如图7所示。

2.2 线圈最优化设计

线圈的最优化设计与磁芯有关，当磁芯材料和几何尺寸确定后，则磁芯质量为定值。为了简便计算线圈质量，定义一个质量因子q，q值等于线圈质量和磁芯质量的比值。如果q存在最优化解，则证明可以满足噪声要求的最佳质量存在。

一般情况下，线圈质量（mw）的表达式为：

mw=π4d2w1γdlmδwn （15）

式中：lm为线圈平均每匝有效长度（mm）;δw为铜线的平均密度（g/cm3）;γd为铜线直径平方与绕线直径平方的比值，d2Cu/d2w。

磁芯质量（mC）和总质量（mS）的表达式为：

mC=π4d3wδC（16）

mS=mw+mC（17）

式中：δC为磁芯总密度（g/cm3）。

增设几何参数，令α=di/d（绕线内径和磁芯直径的比值）;z=do/di（绕线内外径之比）;感应式磁传感器绕组比β=lw/l （绕线长度和磁芯长度之比），β∈（0，1）;绕线填充因子为γw。则质量因子（q）的表达式为：

q=mwmC=（z2-1）α2βγwδwδC（18）

令E=δCα2βγwδw，则z2=1+Eq。则总噪声水平可以用质量因子表示为：

NL=1m53wf ×q83[（1+Eq）12-1]2（19）

质量因子q存在一个最佳值，使感应式磁传感器在质量相同的情况下总噪声水平最小，令NL′=0，得到质量因子的最小值，此处即为最佳质量因子（qopt）的值，如图8所示。

根据最佳质量因子即可确定磁芯质量与线圈质量的比值，此时磁芯质量已定，取质量因子q=qopt，就得到线圈质量唯一值，如图9所示（mwopt即为线圈的最佳质量），因此得到感应式磁传感器满足噪声要求的总质量最佳值mSopt，mSopt=mwopt+mC。

由式（15）可知，线圈质量主要取决于绕线直径和绕线匝数。在线圈质量为mwopt时，最优化绕线直径与绕线匝数使感应式磁传感器的信噪比达到最高。计算不同绕线直径下的线圈总噪声水平，如图10所示，绕线直径的增加在一定程度上降低了整个线圈的噪声水平，但同时提高了线圈的绕组比，增大了线圈质量，因此在设计过程中，需要选择合理的绕线直径。总噪声水平改写为：

NL=qπ4wδC53[（1+Eq）12-1]×1d5w（20）

取NL″=0，得到dwopt，当绕线直径大于dwopt时，二阶导数的符号由正变负，噪声的降低不再明显，则dwopt取为给定质量下的最佳绕线直径。分别在10 Hz、1 000 Hz、10 000 Hz频率处计算噪声水平，其噪声水平值均远小于该频率处的背景场噪声值，证明了优化方法的合理性，如图10所示。348EDD8F-EE9A-4298-8CCE-ABF94DBDD69C

線圈绕线匝数的改变会导致线圈电感与分布电容值的改变，影响谐振频率，从而影响噪声的范围和幅值。通过计算可知，在不同的线圈质量下，每个最佳绕线直径dwopt均对应一个最佳线圈绕线匝数nopt，如图11所示。至此，感应式磁传感器所需的各项参数均已优化完成。

3 最优化设计案例

为了证明此优化设计在实际应用中的可行性，根据最优化公式计算结果绕制1～100 000 Hz感应式磁传感器线圈，并对制得的感应式磁传感器进行测量。感应式磁传感器设计参数如表1所示。

感应式磁传感器加上外壳和灌封胶的实际总质量为2.1 kg，长度为720 mm，满足长度和质量要求;实测噪声功率谱密度如图12所示，均不大于目标参数，满足设计要求。在1 Hz附近，实测噪声功率谱密度受前置放大电路1/f噪声的影响增大，当f>1时，磁芯损耗导致实测噪声功率谱密度大于理论计算值。此外，整个频率范围内实测噪声的功率谱密度均低于地磁场信号功率谱密度，证明最优化设计的结果充分满足要求。

4 结 论

本文在感应式磁传感器噪声源电路的基础上，根据磁传感器设计要求，对感应式磁传感器噪声进行系统分析，根据质量因子分配磁芯与绕线质量，然后根据磁芯长径比和磁芯初始磁导率，对磁芯进行设计优化，最后对绕线进行优化设计，得到最佳绕线直径和最佳线圈绕线匝数，最终得到理论情况下感应式磁传感器的最优化设计方案，并通过实际案例论证方法的可行性。得出如下结论：

1）感应式磁传感器噪声分布与频率有关：当频率小于1 000 Hz时，等效电阻热噪声的影响占主导地位;当频率介于1～10 000 Hz时，等效电流噪声的影响最为明显;当频率大于10  000 Hz时，总噪声水平主要受等效电压噪声的影响。

2）在给定感应式磁传感器设计要求后，感应式磁传感器的制作分为2步：第1步求得满足该噪声水平的磁芯磁导率和长径比参数;第2步通过线圈质量因子计算得到符合设计要求的绕线直径和绕线匝数。

3）该方法通过对感应式磁传感器的噪声进行深入系统的分析，建立数学模型，对设计所需各项参数进行数值计算，使用计算结果制作感应式磁传感器。该优化设计方法计算过程简单，缩短了研制时间，降低了研发成本，具有良好的实用性。

[参 考 文 献]

[1] SRAN H C，FERGEAU P.An optimized low-frequency three-axis search coil magnetometer for space research[J].Review of Scientific Instruments，2005，76（4）：57-65.

[2] 巨汉基，朱万华，方广有.磁芯感应线圈传感器综述[J].地球物理学进展，2010，25（5）：1 870-1 876.

[3] 王勇，佴磊，牛建军，等.高灵敏度感应式磁传感器测试研究[J].地球物理学报，2019，62（10）：3 760-3 771.

[4] 陈兴朋.AMT磁场传感器的研究[D].长沙：中南大学，2012.

[5] TUMANSKI S.Induction coil sensors-A review[J].Measurement Science & Technology，2007，18（3）：31-46.

[6] 孙洁，晋光文，白登海，等.大地电磁测深资料的噪声干扰[J].物探与化探，2000，24（2）：119-127.

[7] SERSON P H.Instrumentation for induction studies on land[J].Elsevier，1973，7（3）：313-322.

[8] PRONENKO V，KOREPANOV V.Induction magnetometers-design peculiarities[J].Sensors & Transducers，2010，120（9）：92-106.

[9] LUKOSCHUS D G.Optimization theory for induction-coil magnetometers at higher frequencies[J].Geoscience Electronics，IEEE Transactions on Geoscience Electronics，1979，17（3）：56-63.

[10] BARSUKOV P O，FAINBERG E B.Marine transient electromagnetic sounding of deep buried hydrocarbon reservoirs：principles，methodologies and limitations[J].Geophysical Prospecting，2016，65（3）：1-19.

[11] TIMOFEEVA M，GILLES A，ROBBES D，et al.Differential search coils based magnetometers：conditioning，magnetic sensitivity，spatial resolution[J].Sensors & Transducers，2014，14（Special Issue）：134-150.

[12] GROSZ A，PAPERNO E.Analytical optimization of low-frequency search coil magnetometers[J].IEEE Sensors Journal，2012，12（8）：2 719-2 723.348EDD8F-EE9A-4298-8CCE-ABF94DBDD69C

[13] LIU L，LIU K，YAN B，et al.Equivalent input magnetic noise analysis for the induction magnetometer of 0.1 mHz to 1 Hz[J].IEEE Sensors Journal，2014，14（12）：4 442-4 449.

[14] KAAPLAN B Z，SUISSA U.Treatment of extremely low frequency magnetic and electric field sensors via the rules of electromagnetic duality[J].IEEE Transactions on Magnetics，1998，34（4）：2 298-2 305.

[15] POLIAKOV S V，REZNIKOV B I，SHCHENNIKOV A V，et al.The range of induction-coil magnetic field sensors for geophysical explorations[J].Seismic Instruments，2017，53（1）：1-18.

[16] ROUX A，CONTEL O L，COILLOT C，et al.The search coil magnetometer for THEMIS[J].Space Science Reviews，2008，141：265-275.

[17] PAPERNO E，GROSZ A.A miniature and ultralow power search coil optimized for a 20 mHz to 2 kHz frequency range[J].Journal of Applied Physics，2009，105（7）：2-3.

[18] 陈志毅，周穗华，吴志东.低频感应式磁传感器优化设计[J].四川兵工学报，2013，34（4）：123-126.

[19] 邵英秋，程德福，王言章，等.高灵敏度感应式磁传感器的研究[J].仪器仪表学报，2012，33（2）：349-355.

[20] 应毓海.基于磁通负反馈的低噪声宽频带感应式磁传感器设计[J].传感器与微系统，2014，33（12）：67-69，75.

Optimal design of inductive magnetic sensors based on noise level

Du Zheng1，2，Chen Xingpeng3，Xi Zhenzhu1，2，Tang Yao1，2

（1.Key Laboratory of Non-ferrous Metals Metallogenesis Prediction，Central South University，Ministry of Education;

2.School of Geosciences and Info-physics，Central South University;

3.Hunan Wuwei Geological Technology Co.，Ltd.）

Abstract：Magnetotelluric inductive magnetic sensors are one of the most common instrument used in geophysical exploration.Noise level is the core technical index of magnetoteluric inductive magnetic sensors.The designers of inductive magnetic sensors have been long bothered by its long development period and low design efficiency.So it is necessary to optimize the design method to shorten the period and improve efficiency.First of all，the paper theoretically analyzed the noise distribution rules of inductive magnetic sensors in different frequency.Given design requirements of the inductive magnetic sensors，the paper constructed the function between of noise，ratio of magnetic core length and diameter and magnetic conduction rate，and obtained the optimal magnetic core mass that met the design requirement; then，a mass factor was defined in order to construct the function between noise and mass factor.By calculation of the coil mass，the optimal diameter of the wire was obtained.At the same time，with the defined coil ratio of inductive magnetic sensors，the paper by calculation determined the coil turns;finally a 1-100 000 Hz inductive magnetic sensor was designed and prepared with the above methods that were tested.The results show that its noise level in the frequency range meets the design requirement，indicating the reasonability of this optimal design.

Keywords：inductive magnetic sensor;noise level;optimal design;mass factor;actual measurement

收稿日期：2021-11-18; 修回日期：2022-01-20

基金項目：国际海域资源调查与开发“十三五”项目（DY135-S1-1-07）

作者简介：杜 政（1997—），男，甘肃庆阳人，硕士研究生，研究方向为地球物理仪器研发;长沙市岳麓区潇湘中路，中南大学地球科学与信息物理学院，410083;E-mail：962508006@qq.com348EDD8F-EE9A-4298-8CCE-ABF94DBDD69C