基于改进PSO-TrICP算法的点云配准
梁正友,王 璐,李轩昂,杨 锋
(1.广西大学计算机与电子信息学院,广西 南宁 530004; 2.广西多媒体通信与网络技术重点实验室,广西 南宁 530004)
0 引 言
点云配准是通过求取点云间的空间变换参数,将不同场景、不同时刻采集的点云数据对齐至同一空间坐标系的过程[1]。其中,点云的粗配准以快速地估计点云的刚性变换为目的[2],广泛运用于虚拟现实、即时定位与地图构建、航天影像等领域[3-4]。1992年,Besl等人[5]提出的ICP算法通过估计点云间的旋转参数R∈3×3及平移参数T∈3×1,最小化点云间的空间偏差,是一种常用的配准算法,但ICP算法存在对点云的初始空间位置要求高,且点集规模较大时运行速度慢的缺点。因此,许多研究者对该算法进行了改进[8-10]。Chetverikov 等人[8]针对仅存在部分重叠的点云配准需求提出了一种TrICP算法,通过估计点云间的重叠率,最小化点云间的均方根距离,从而提升点云的配准质量;Li等人[9]利用K-D树结构存储点云数据并将其用于搜索点云的邻域,使数据在得到高效管理的同时提升了配准精度;杨小青等人[10]将点云的法向量夹角和曲率用于查找对应点集,并通过计算点对的距离和高斯曲率两重约束获取匹配点,能够得到可靠且高效的配准结果。
近年来,由于智能算法对最优解问题具有优势,吸引了研究者将其引入点云配准技术中[11-14]。Chen等人[11]提出一种将增强人工蜂群算法用于三维点云配准的方法,提升了配准效率;Lomonosov等人[12]提出了一种利用遗传算法(Genetic Algorithm, GA)对任意取向的三维曲面配准的方法,该方法能够完成搜索空间内任意方位点集的粗配准;Zhu等人[13]提出了一种将GA算法结合TrICP算法的多视图配准技术,通过进化算法中的遗传和变异等操作估计点云初始位置,能够得到准确的刚性变换参数;Yan等人[14]为结合GA算法的配准技术提出了一种新的适应度函数,满足了配准需求。
Kennedy和 Eberhart提出的PSO算法[15]是一种常见的群体智能算法,能够为任意取向的点云提供一个良好的初始位置,从而获得更准确的配准结果[16-18]。Zhan等人[19]提出了一种基于熵和PSO算法的配准方法,能够达到抑制噪声,有效提高配准精度的效果;Ge等人[20]同样运用了PSO算法,通过限制法向量方向及对应点距离等方法提升了配准精度;Zhang等人[21]提出将多层粒子群优化算法应用于配准,从而取得良好的效果,但该方法的运行时间较长;Yang等人[22]提出了一种将PSO算法结合ICP算法的配准,但该方法耗时较长,且无法完全避免配准结果陷入局部最优。综上所述,结合智能算法的点云配准方法需要在保证配准性能的同时提升运行效率,成为有待解决的问题。
因此,针对点云处于任意初始空间位置的情况,本文提出一种基于改进PSO-TrICP算法的点云配准方法。首先对传统PSO算法改进,添加了相似度测量准则和新的学习因子提升算法的寻优能力,其次利用改进的PSO算法的随机搜索机制构造初始粒子群,最后通过TrICP算法在迭代中求取刚性变换参数,得到最终的配准结果。在Stanford点云数据集和Kinect v2所采集的三维人体模型数据集上进行实验的结果表明,本文方法的配准精度及运行效率优于其他配准方法,且具有较好的鲁棒性。
1 基础算法介绍
1.1 传统PSO算法
PSO算法[15]模拟鸟群生存过程中的捕食行为:鸟类个体依靠自身经验与其他成员间的信息交流调整搜索路径,最终抵达食物最多的场所,具有无需梯度信息且所需参数少的特点[24-25]。
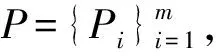
(1)
(2)
其中,ω是取值范围在0~1之间的惯性参数,c1和c2分别是粒子的认识系数和社会系数,通常取值为2;rand()是取值范围在0~1间的随机数。
1.2 TrICP算法
TrICP算法[8]是一种改进的ICP算法,通过裁剪点云之间重叠部分的数据点,避免构成错误的点对关系,提升了配准的精度和效率。假设存在部分重叠的点云Q和点云O,初始化重叠率为ζ,且ζ∈[ζmin,ζmax];点云Q中共包含N个点,其中,只有ζ×N个点与点云O存在正确的匹配点。因此,从点云Q中提取ζ×N个点构成特征点集QF,并计算点云QF和点云O间的刚性变换参数(R,T),得到最终的配准结果。
在迭代过程中,TrICP算法提取对应点集的描述如下:
假设qi是点云Q中的点,根据初始空间变换矩阵(R,T),则qi与点云O的对应关系如公式(3):
(3)
计算个体距离ri:
ri=‖ocl(i,R,T)-(Rqi+T)‖
(4)
对ri进行增序排列:
(5)
其中,N′=ζ×N。
根据重叠率ζ从点云Q中提取特征点集QF={q1,q2,…,qN′},STS是点集QF到点云O的距离之和:
(6)
计算最小化平均距离SN′:
(7)
根据SN′结合黄金分割原理更新重叠率ζ,参数λ通常设置为2:
(8)
TrICP算法的详细步骤见算法1。
算法1TrICP算法
输入:点云Q和点云O、最大重叠率ζmax、最小重叠率ζmin、最大迭代次数M
输出:刚性变换矩阵(R,T)
Begin:
m=0;
Repeat:
m=m+1;
根据公式(3)建立点云间的对应关系;
根据公式(4)获取个体距离ri;
根据公式(6)计算距离之和STS;
求取点云Q和点云O间的刚性变换矩阵(R,T);
根据公式(7)和公式(8)更新重叠率ζ;
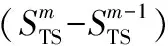
小于设定阈值
End
2 提出的方法
2.1 改进的PSO算法
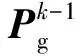
(9)
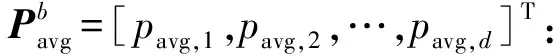
(10)
在添加新的学习因子后,计算粒子速度的公式为:
(11)
2.2 基于改进PSO-TrICP的点云配准算法
针对空间内任意初始位置的点云粗配准问题,本文结合改进PSO算法和TrICP算法提出一种新的点云配准方法,利用改进的PSO算法为点云之间提供良好的相对位置,并通过TrICP算法裁剪重叠部分的点云提升配准质量,克服传统配准算法对点云的初始相对位置要求高、容易陷入局部最优等缺点。
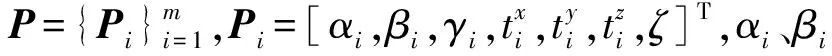
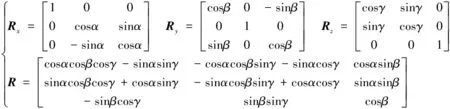
(12)
接着,将粒子群Pi作为初始空间变换参数,通过TrICP算法计算得到新的(R,T)及适应度,粒子群的适应度函数计算公式为:
fitness(Ri,Ti,ζi)=EXP(-SN′)
(13)
基于改进PSO-TrICP的点云配准算法的详细步骤见算法2。
算法2基于改进PSO-TrICP的点云配准算法
输入:点云Q和点云O,最大迭代次数K
输出:刚性变换矩阵
Begin:
k=0;
初始化粒子群P;
Repeat:
k=k+1;
根据算法1计算粒子适应度并更新粒子;
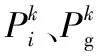
If持续x轮迭代U(k)<ε
根据公式(2)和公式(11)更新粒子;
Else
根据公式(1)和公式(2)更新粒子;
End
Untilk>K
End
3 实验与结果分析
3.1 实验建立与评价指标
为了验证本文提出算法的可靠性和高效性,本文采用Stanford三维点云数据集和Kinect v2采集的三维人体模型数据集为例。其中,Stanford三维点云数据集分别包括Bunny、Armadillo、Dragon及Buddha,模型图像如图1所示,点云详情如表1所示;三维人体模型数据集包括身高为0.90 m的男童人体模型和身高为1.80 m的女性人体模型,如图2所示。实验使用Windows 10(64位)的操作系统、Intel(R)Core(TM)i5-8250U CPU@1.60 GHz的计算机,代码通过Matlab2018b实现。

图1 Stanford三维点云数据集在不同角度的点云图像
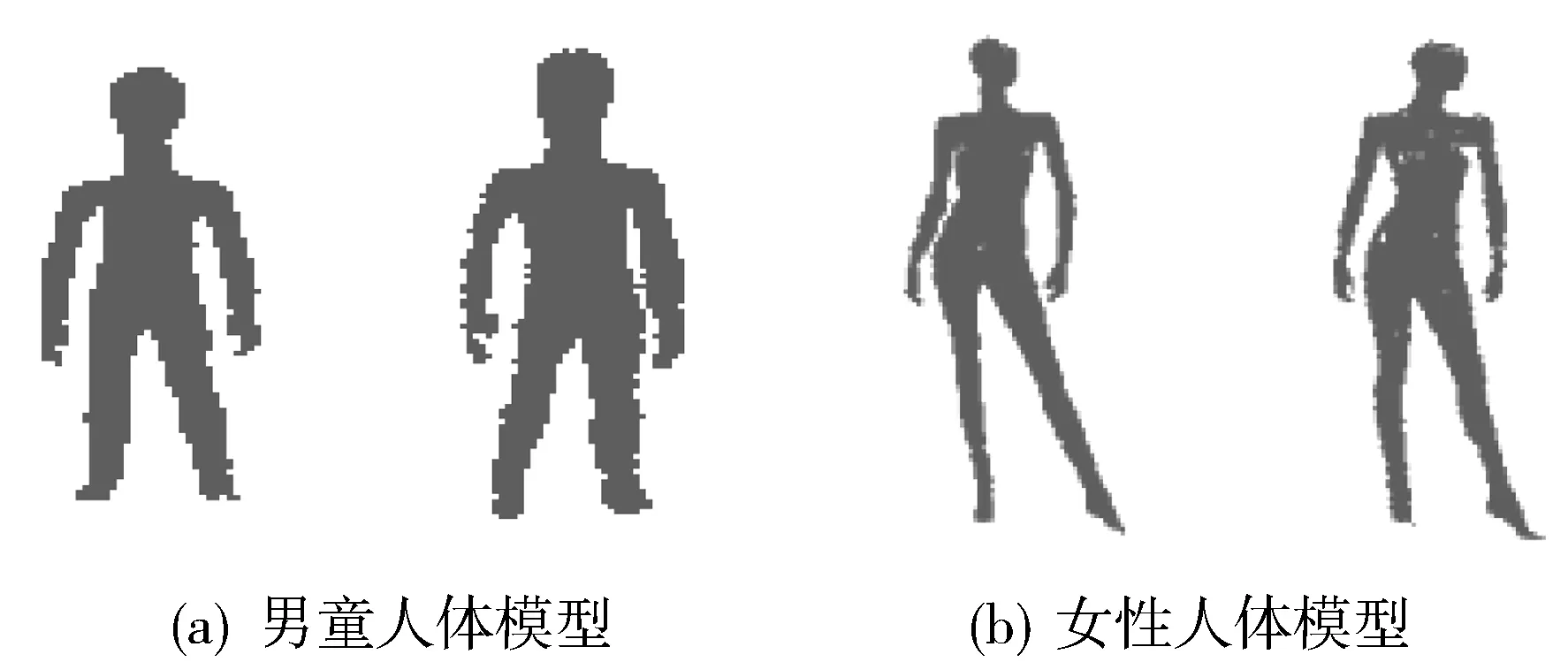
图2 三维人体模型数据集在不同角度的点云图像
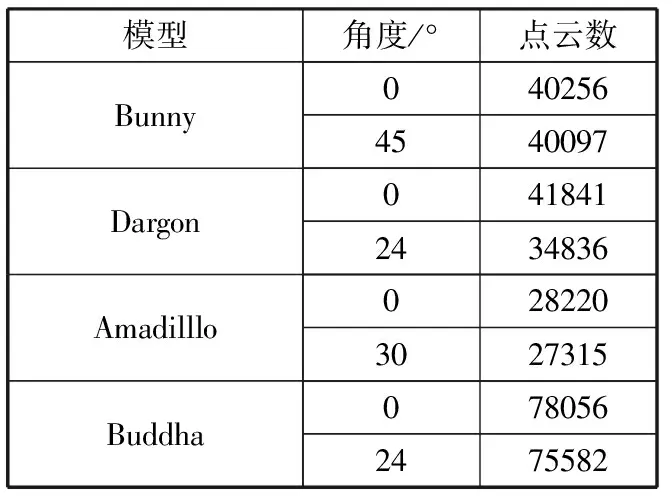
表1 点云详情
为消除实验过程中的随机性,本文对各算法分别进行50次蒙特卡洛实验,并取其旋转误差ER、平移误差ET(·10-3·m)及运行时长的均值。设为点云添加的随机真实值为[Rg,Tg],通过配准算法得到的刚性变换矩阵为[Rw,Tw],则旋转误差ER的度量公式表示为:
ER=‖Rw-Rg‖F
(14)
平移误差ET的度量公式为:
ET=‖Tw-Tg‖2
(15)
3.2 对比试验与结果分析
为描述本文方法的性能,实验采用4种配准算法与其对比,分别包括ICP算法[5]、TrICP算法[8]、PSO-ICP算法[22]和GA-TrICP算法[13]。
3.2.1 点云配准精度
图3、图4和表2分别描述了不同算法对各模型的配准可视化图及精度。可以看出:ICP算法和TrICP算法受初始空间位置的影响容易陷入局部最优,从而导致配准失败;PSO-ICP算法的配准精度较差;GA-TrICP算法与本文方法相比,配准的精度较低,但能够满足空间内任意取向点云的配准需求,利用智能算法在搜索空间内获得良好的初始位置,通过评估刚性变换参数的优劣,从而使配准结果趋于最优解,提升了点云配准的精度。

图3 Stanford三维点云模型在各算法下的配准结果
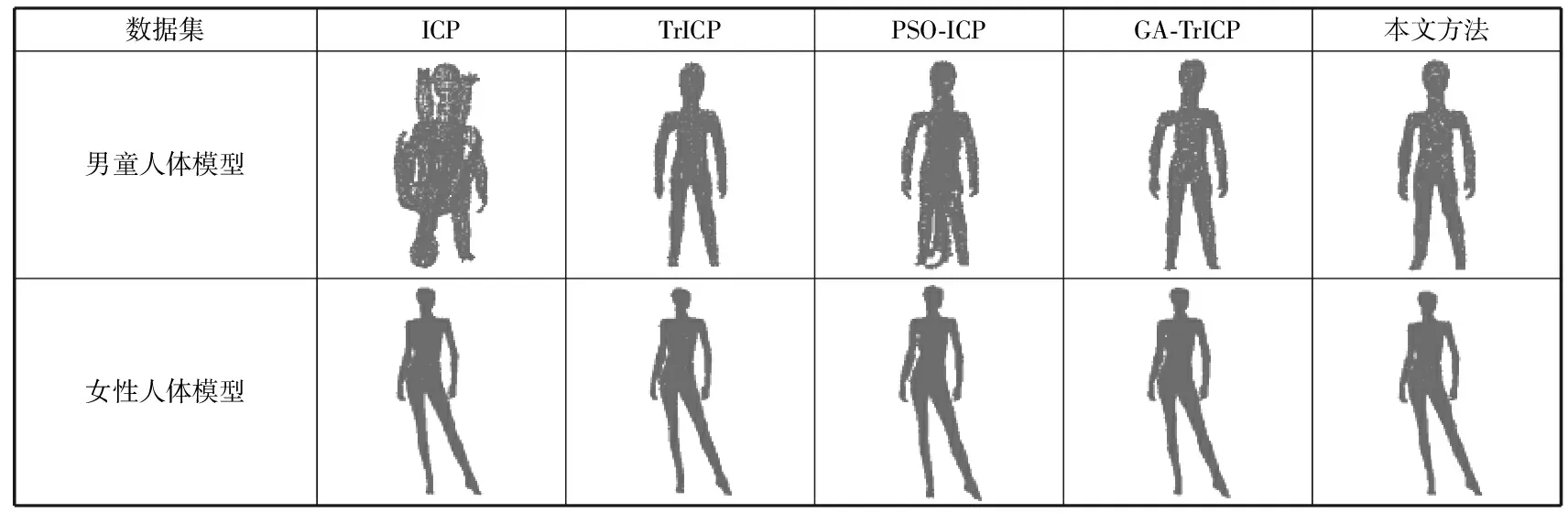
图4 三维人体点云模型在各算法下的配准结果
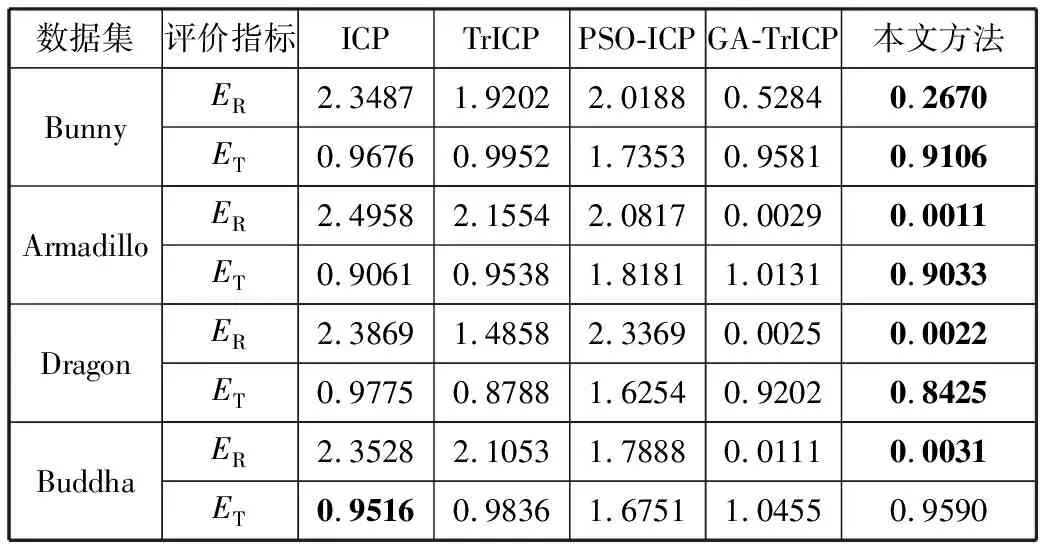
表2 不同算法对各模型配准精度的比较
3.2.2 点云配准效率
表3为不同算法对各模型配准的运行时长,可以看出ICP算法和TrICP算法是高效的,但这是以配准失败或损失配准精度为前提的;PSO-ICP算法受到迭代最近点算法效率的影响,与本文方法相比,无法获得较高的效率;GA-TrICP算法和本文方法都利用TrICP算法计算刚性变换参数,通过对点云重叠部分进行裁剪,减少了算法运算量,从而提升了配准效率。
3.2.3 点云配准鲁棒性
为了更好地描述本文方法的鲁棒性,本文为各个模型分别添加[-0.02f, 0.02f]的高斯噪声,配准的结果如表4所示。可以看出本文方法能够完成具有噪声的点云配准,且精度优于对比的配准算法。
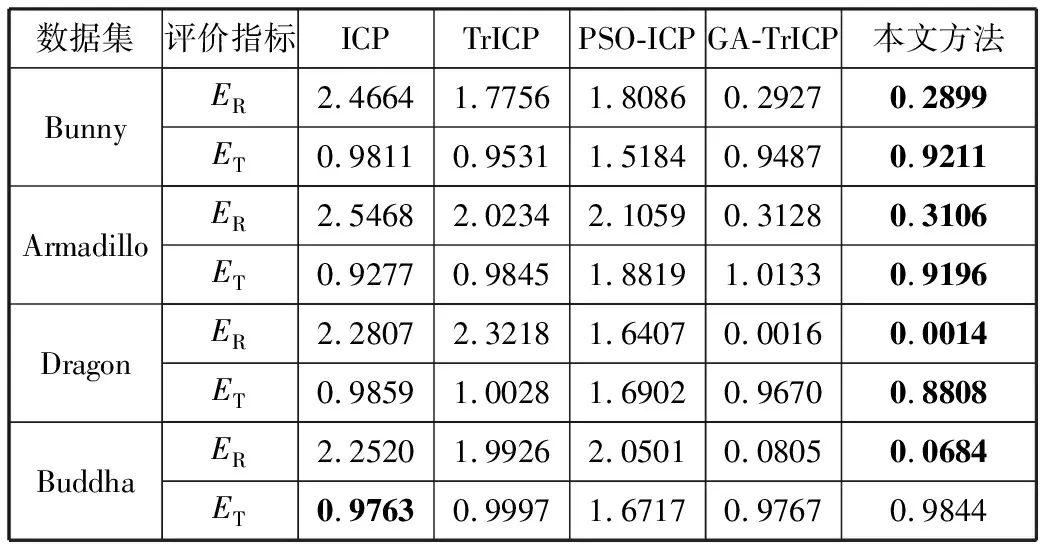
表4 不同算法在添加[-0.02f, 0.02f]高斯噪声后,点集的配准精度的比较
综上所述,本文提出的改进PSO-TrICP算法在配准实验中能够在Stansford点云数据集中取得较好的结果,同时适用于本文用Kinect v2采集的人体数据集。比较其他方法,本文提升了配准的精度及效率,且具有较强的鲁棒性。
4 结束语
针对空间内任意初始位置的点云粗配准问题,本文提出了一种基于改进PSO-TrICP的点云配准算法。首先为传统PSO算法增加了相似度测量准则和新的学习因子,其次通过改进的PSO算法将点云间的刚性变换参数及重叠率作为粒子,最后利用TrICP算法求取点云间的刚性变换矩阵,从而得到最终的配准结果。实验结果表明了改进PSO-TrICP算法的可靠性和高效性,且该方法对包含噪声的点云配准依然有效。

