基于导线动态张力的覆冰质量计算方法

胡建林，王晓枫，王文淞，叶铭境，张 翕

（重庆大学输变电装备及系统安全与新技术国家重点实验室，重庆 沙坪坝 400044）

近年来，覆冰灾害事故在我国时有发生，给电网和国民经济带来的损失不可估量[1-3]，针对电网冰灾防治的研究已开展多年，极大的改善了电网对于冰灾事故的抵御能力，但电网冰灾防治从未在根本上得到解决，重要原因之一便是无法准确监测导线覆冰。现在，较为精准的输电线路覆冰监测方法主要以力学模型监测为主，视频图像监测为辅[4-8]，但是野外覆冰往往伴随着大风天气，自然界中风是时变的，因此采集到的是动态拉力信号，须研究瞬时风荷载、冰荷载与覆冰导线端部动态张力的关系。

目前，国内外已经开展大量导线覆冰参数计算的研究[9-11]，但是多数是在无风以及平均风条件下进行的，往往须结合倾角传感器采集覆冰导线角度数据。文献[12]提出了架空线路耐张塔理论覆冰计算模型及简化模型，研究了不同绝缘子串型下的模型，并对包括风偏角及倾斜角、拉力传感器误差、垂直档距和拉力传感器个数等直线塔计算模型影响因素进行了分析，发现风偏角不超过20°时，耐张塔理论模型和简化模型均可不考虑风偏对冰厚计算的影响。文献[13]在现有计算模型基础上，运用力学原理，结合导线自然覆冰增长特性，综合考虑风荷载对覆冰导线荷载特性的影响，系统地建立了绝缘子串不同布置方式下（耐张串、Ⅰ串和V串）的综合荷载等值冰厚计算模型，模型须输入绝缘子悬挂点拉力、倾角数值，使用长时段平均风偏角模型时具有高精度。文献[14]考虑了导线绝缘子及金具上覆冰质量对等值冰厚计算模型的影响，提出了考虑导线由覆冰荷载引起应变的绝缘子串拉力/倾角-输电线路等值覆冰厚度计算公式，试验时发现受到外力干扰时导线倾角与偏角的波动幅度很大，对于等值冰厚计算有很大影响。

本文研究了基于导线动态张力的覆冰质量计算方法。根据现有的输电线路力学模型，不使用导线倾角、偏角数据，确定瞬时风荷载、冰荷载、温度变化与导线端部张力定量关系，提出风荷载系数Kf以计算不同覆冰情况下瞬时风荷载，以此为基础确定导线覆冰质量计算方法，并进行野外覆冰试验验证方法有效性。

1 覆冰导线力学计算

为了方便覆冰导线力学计算分析，须进行以下假设[15]：

导线是理想柔性索结构，既不能受压，又不能抗弯。导线的截面尺寸与其长度比值很小，因此在计算中可以不用考虑截面的抗弯刚度。

导线材料符合虎克定律，导线工作范围处在弹性阶段。

覆冰沿导线跨度均匀分布，并且不改变导线本身材料及结构属性。

1.1 覆冰导线构型计算

导线构型一般有悬链线与抛物线两种，当导线垂度即f/L小于0.125时，抛物线与悬链线差值很小，导线抛物线公式满足计算精度需求，为了简化计算，一般采用导线抛物线公式[16]。

对于均匀覆冰的导线，可以近似认为导线只承受竖向荷载。沿导线跨度均匀分布的冰荷载为q，自重荷载为q0，则qx=0，qz=q+q0，通过水平拉力H0得到导线覆冰之后的抛物线公式：

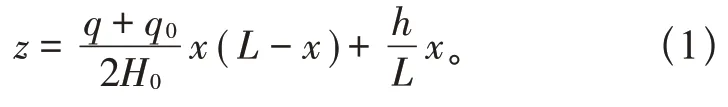
在实际应用中，输电导线水平张力很难测量得到，通常只能采集到输电导线端部的轴向张力，通过构型式（1）可得导线低挂点张力为：

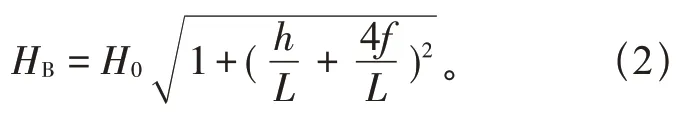
式中：L为输电导线档距，m；h为输电导线高差，m；HB为导线低挂点端部轴向张力，N；H0为导线水平张力，N。

当高差h=0 时，此时轴向张力HB值最大，当垂跨比f/L小于0.125 且取不同值时，最大轴向张力与水平张力比值与随垂跨比变化如表1所示。由表1可以看出，当垂跨比小于0.075时，最大轴向张力与水平张力只相差4%，当高差存在时，低挂点轴向张力更接近水平张力，所以当垂跨比小于0.075时，可以使用导线低挂点张力替代水平张力。

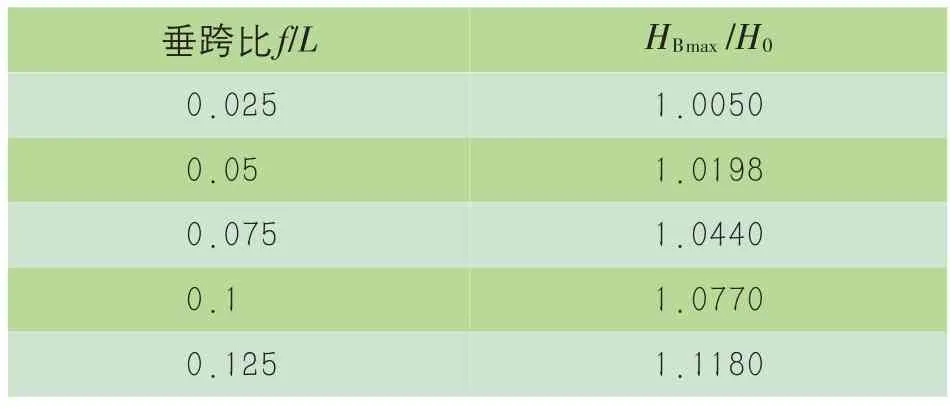
表1 导线垂跨比对悬挂点张力与水平张力比值影响

1.2 覆冰导线静张力计算

导线覆冰往往伴随着温度的降低，此时温度改变所带来的导线长度的变化不能忽略。从运动角度考虑，当没有瞬时风影响时，导线只受自重及覆冰重量的影响，导线发生平面内形变；从物理角度考虑，导线伸长量与张力变化相关，结合温度的影响，最终得到导线变形协调方程：

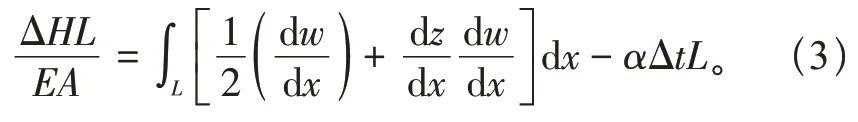
导线上增加均匀覆冰载荷q后，导线到最终状态是满足变形协调方程，根据式（1），可以得到导线覆冰后水平张力H1与覆冰前水平张力H0差值公式为：

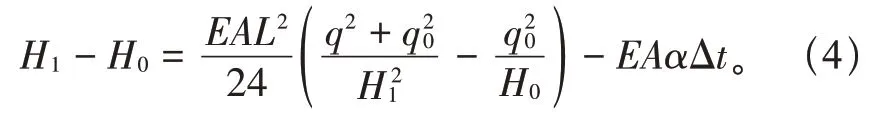
式中：E为杨氏模量，Pa；ΔH为覆冰前后导线水平张力改变量，N；A为导线计算截面积，m2；α为导线温度膨胀系数；Δt为覆冰前后温度改变量，℃。

1.3 瞬时风荷载下覆冰导线拉力计算

以如图1 所示一档覆冰导线为研究对象，覆冰导线YOZ平面构型投影如图2所示。

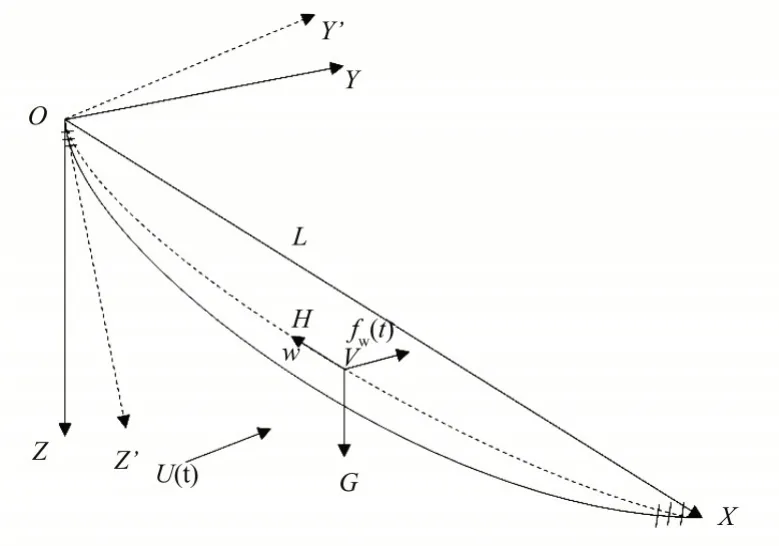
图1 瞬时风荷载下导线整体构型

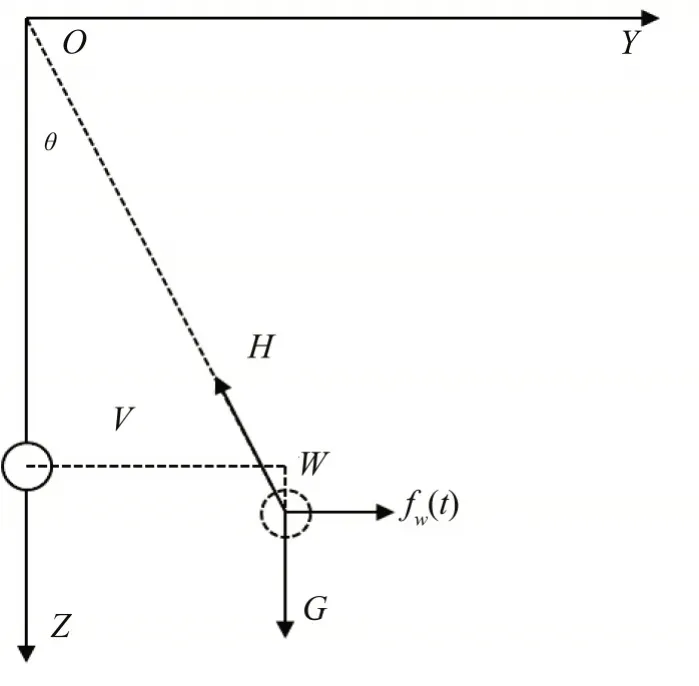
图2 导线构型YOZ平面投影

导线初始构形采用抛物线公式，导线初始状态水平张力为H0，覆冰后导线静态水平拉力为H1，风荷载fw(t)作用下，覆冰导线动态水平张力为H(t)，覆冰导线单元顺风向（y轴向）位移为v(x,t)，竖向（z轴向）位移为w(x,t)。忽略导线动张力响应的共振分量[17]，在风荷载、冰荷载以及自重荷载共同作用下覆冰导线动力方程组为[18]：

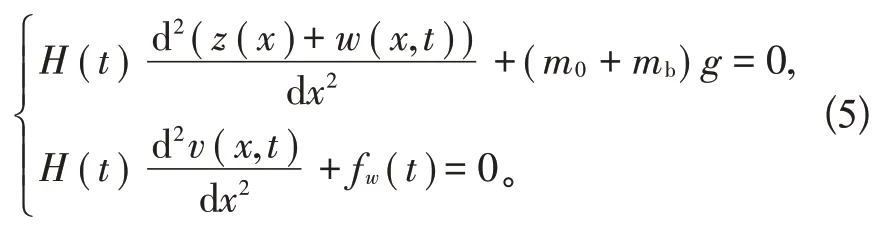
将边界条件及导线变形协调方程带入式(5)展开化简，得到覆冰导线水平动态张力、温度、冰荷载以及瞬时风荷载定量关系方程：

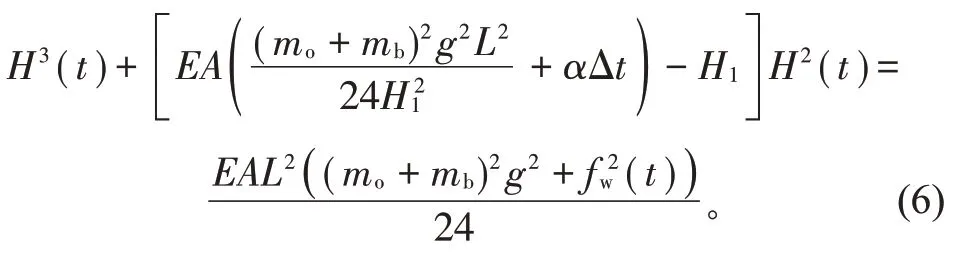
式中：m0为导线单位长度质量，kg；mb为导线单位覆冰质量，kg；g为重力加速度，m/s2。

2 基于动张力的导线覆冰质量计算方法

2.1 风荷载计算系数

覆冰导线单位长度瞬时风荷载为[19]：

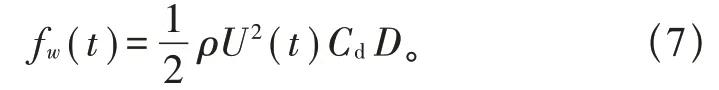
式中：U(t)为风速，m/s；ρ为空气密度，kg/m3；Cd为覆冰导线气动阻力系数；D为覆冰导线迎风长度，m。

覆冰形状、覆冰厚度以及瞬时风参数都能显著改变导线气动阻力系数[20]。自然条件下，导线覆冰一般都是不规则形状，覆冰导线气动阻力系数难以使用仿真以及风洞试验计算，因此须先确定不同覆冰情况下风荷载与瞬时风速关系。

大风往往伴随着覆冰增长，输电线路一般处于拉紧状态，少量覆冰质量增长就会引起覆冰导线端部张力较大增加[21]，因此自然状态下针对覆冰导线瞬时风荷载的研究须截取合适时间段Δt，认定Δt内，覆冰质量增长可以忽略，覆冰导线端部张力变化只与风荷载有关。时间段Δt可以根据历史气象、统计覆冰数据确定。

将覆冰导线视为一个整体，由式（7）可知风荷载与风速二次方相关，对于小档距导线，风压不均匀系数为1，风荷载系数Kf与瞬时风速关系：

式中：v(t)为有效瞬时风速，忽略顺风向风速，取最不利攻角情况，m/s。

Δt内，将覆冰导线动态张力带入式（6），计算瞬时风对应风荷载，根据式（8）计算风荷载系数，进行拟合可以得到导线当前覆冰情况风荷载系数与风速的数值关系。

2.2 导线覆冰质量计算思路

在无风或软风条件（有效瞬时风速＜临界风速）时，覆冰导线可以认为是静态的，将覆冰前后导线低挂点张力及温差带入式（4）便可以计算出导线覆冰质量，临界风速可以根据历史气象数据及张力数据确定。在起风后，在短时间Δt内覆冰质量不增加，导线张力改变量只与瞬时风速有关，将导线张力数值带入式（6）计算出瞬时风荷载，拟合出该覆冰形态下风荷载系数随风速的函数关系式，根据该系数计算出后续覆冰增长情况下瞬时风荷载，再将瞬时风荷载带回式（6），计算出导线覆冰质量，求取Δt内平均值就得到Δt时间内覆冰质量。覆冰导线覆冰质量计算结构如图3所示。

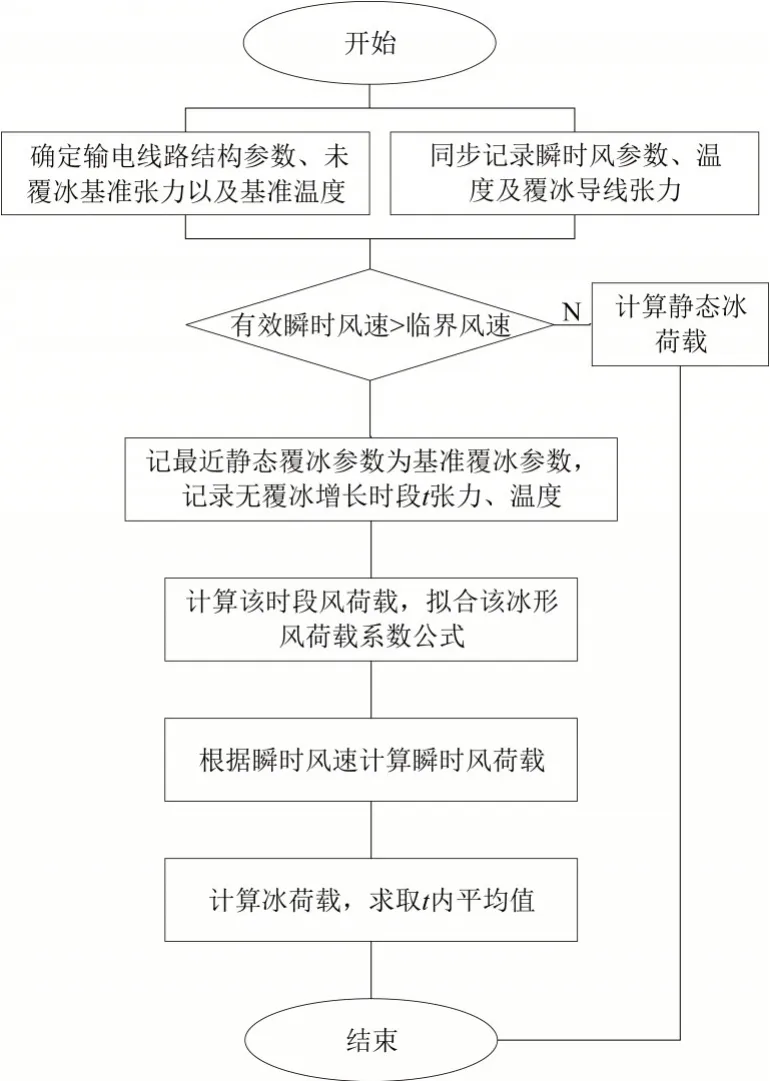
图3 瞬时风下导线覆冰质量计算结构图

3 野外覆冰试验验证及误差分析

3.1 试验设置及方法

本文于重庆大学雪峰山野外站对其中的试验单导线段、钢绞线段（下简称：试验导线）在自然覆冰的动态张力以及同步自然瞬时风速开展了测量试验。两条试验导线具体数据如表2所示。

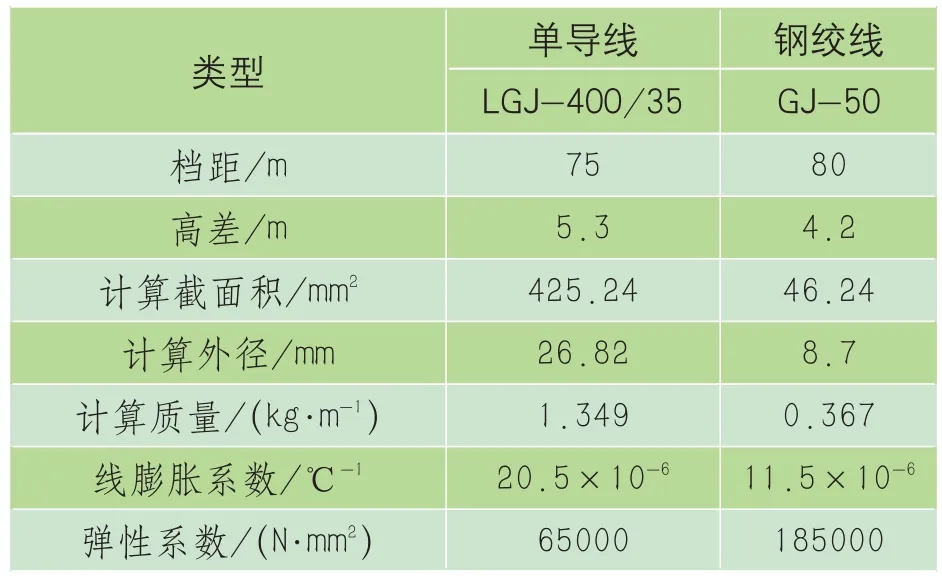
表2 试验线路导线结构参数表

采用DYLY-101柱式S型拉力传感器测量试验导线端部轴向张力；采用防覆冰风压风速计，该风速计能够精确测量3 s瞬时风速、风向，并且可以在覆冰低温环境下持续工作；两种装置均可以通过E22模块无线传输两种方式传输到计算机中，实现动态张力及瞬时风速同步采集；为了保证导线覆冰完整性，单位覆冰质量须由等值冰厚计算，将根据覆冰长度及厚度带入式（9）换算等值冰厚，根据等值冰厚带入式（10）计算单位长度覆冰质量[20]。

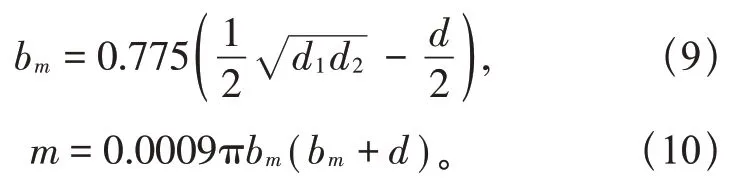
式中：bm为等值覆冰厚度，mm；d为裸导线直径，mm；m为导线单位长度覆冰质量，kg；d1、d2分别为覆冰导线的直径与覆冰的厚度，mm。

以正北向为风向角0°方向，试验导线布置方式如图4所示，参与计算的有效风速由式（11）计算。

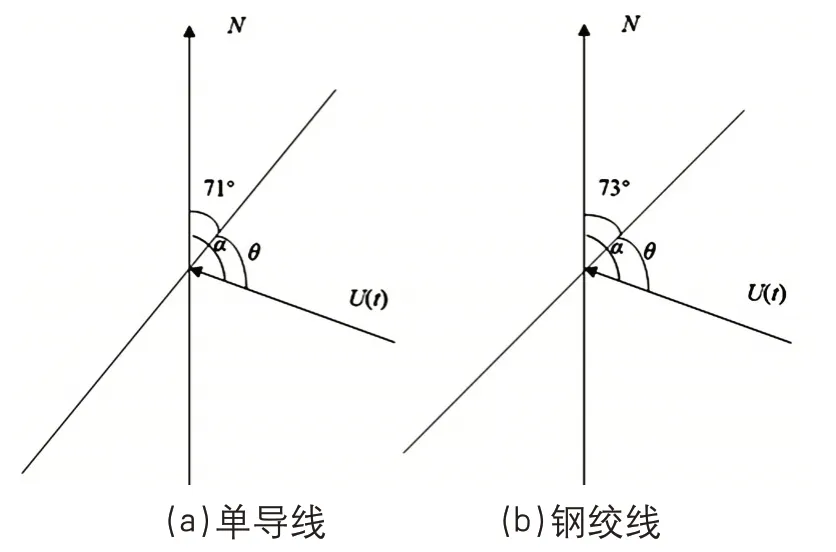
图4 试验导线布置俯视示意图

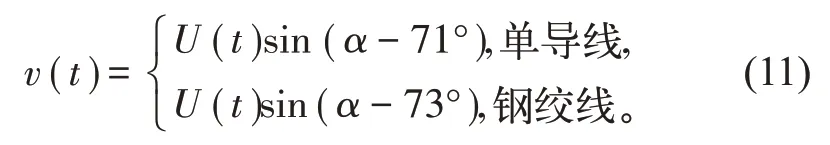
式中：v(t)为横线路方向有效风速，m/s；U(t)为瞬时风速，m/s。

3.2 无风条件下覆冰试验结果

两档试验导线均处于拉紧状态，试验期间垂跨比远小于0.0075，使用导线低挂点轴向张力代替水平张力；于雪峰山野外站试验期间，采集到的瞬时风速变化在0.5～11.5 m/s 之间，风向角变化在110°～200°之间；当风速v≤1.5 m/s，导线拉力曲线并未随风速发生明显震荡变化，经过整个试验过程试验导线端部拉力统计分析，均方差小于5 N，可以将基准风速设置为v=1.5 m/s。根据现场测量及拉力数据统计分析，可以认为导线覆冰在300 s 内没有增长，所以Δt取300 s。

选取瞬时风速小于基准风速时覆冰导线端部张力及温度数据，结合无冰无风情况下试验导线端部基准张力、温度带入式(4)，计算导线单位覆冰质量，不同覆冰状态下计算值与测试值比较如表3所示。

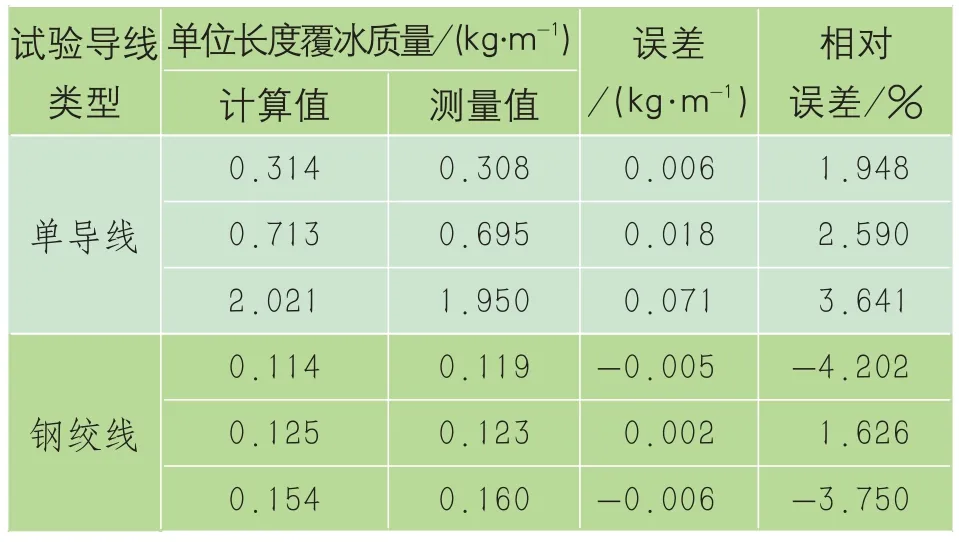
表3 试验导线静态时单位覆冰质量对比

由试验结果可以看到，只考虑冰荷载静力作用低悬挂点张力计算值与实测值误差很小，最大相对误差4.202%，能够满足工程计算精度需求。造成误差原因主要有两点：人为测量造成误差，由于实验过程中，导线覆冰全部是不规则的，覆冰形状不规则造成覆冰质量测量存在一定误差；绝缘子及金具上覆冰质量造成误差，由于试验单导线端部的张力传感器加装在绝缘子及雨凇塔之间，覆冰后静态张力变化量包含绝缘子及金具上的覆冰质量，造成覆冰质量计算值增大，随着覆冰质量增加，误差越来越大。

3.3 瞬时风条件下覆冰试验结果

冰期1钢绞线覆冰情况如图5所示，覆冰形状较规则的翼型且覆冰较薄。当日9:44 瞬时风速开始增长，瞬时风速在1～8 m/s内波动。

图5 试验导线覆有规则薄冰情况

将试验导线未覆冰时基准张力、基准温度以及覆冰后低挂点张力、温度带入式（4）计算风速增长前300 s内导线基准覆冰质量。再根据覆冰导线静态参数、覆冰导线低挂点动态张力值计算300 s 风荷载，根据有效瞬时风速三次多项式拟合风荷载系数曲线如图6 所示，相关系数R2=0.961，具有较好的拟合度。

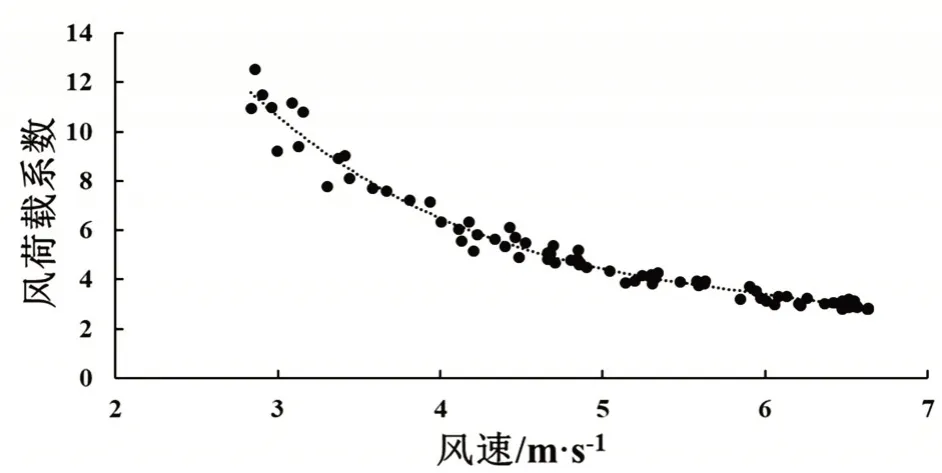
图6 覆有规则薄冰试验导线风荷载系数

将有效瞬时风速值带入风荷载系数函数中，求出瞬时风荷载，最后根据风荷载计算出试验导线冰荷载。该日9:00～12:00试验导线单位长度覆冰质量计算与试验对比如图7 所示，具体数值对比及误差如表4所示。

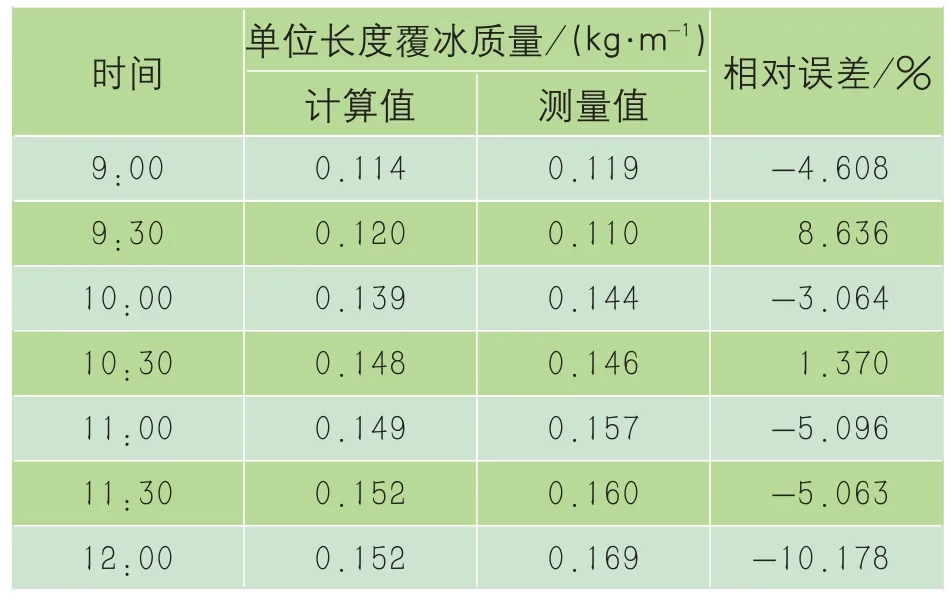
表4 覆有规则薄冰时单位长度覆冰质量对比

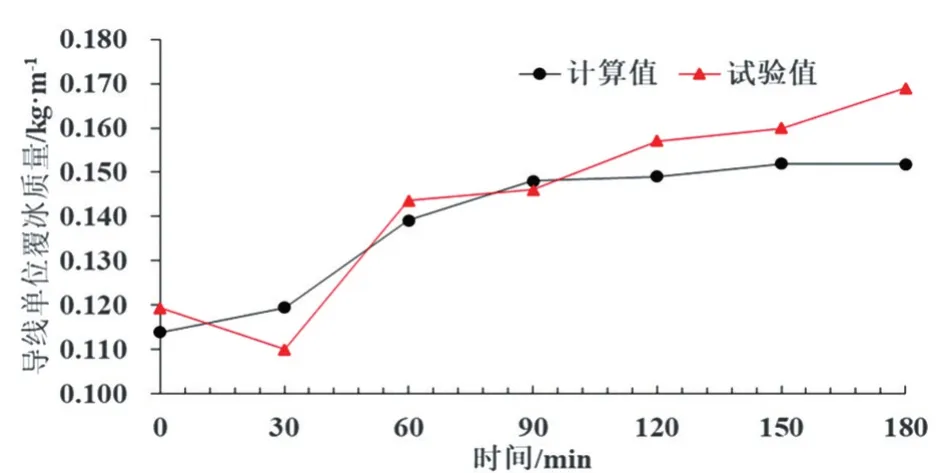
图7 覆有规则薄冰单位长度覆冰质量计算值与测试值

冰期2 单导线覆有不规则厚冰情况时，如图8所示，当日瞬时风速在0.5～10 m/s 内波动，从8:55瞬时风速开始增长，以相同方法，拟合风荷载系数曲线如图9所示，相关系数R2=0.959，具有较好的拟合度。

图8 试验导线覆有不规则厚冰情况

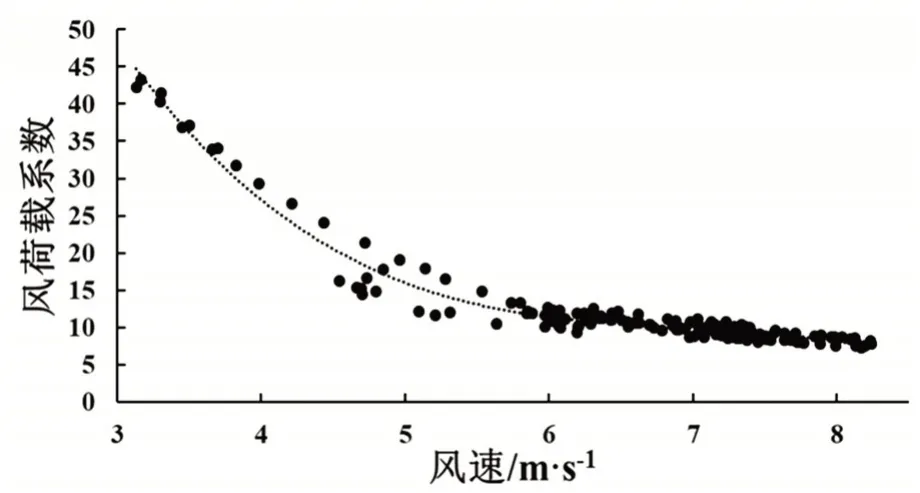
图9 覆有不规则厚冰试验导线风荷载系数

该日9:00～12:00试验导线单位长度覆冰质量计算与试验对比如图10所示，具体数值对比及误差如表5所示。

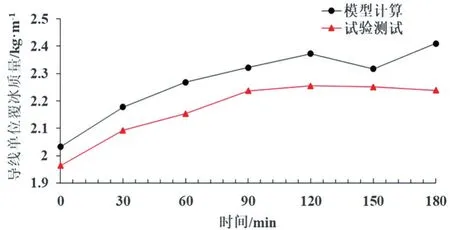
图10 覆有不规则厚冰单位长度覆冰质量计算值与测试值

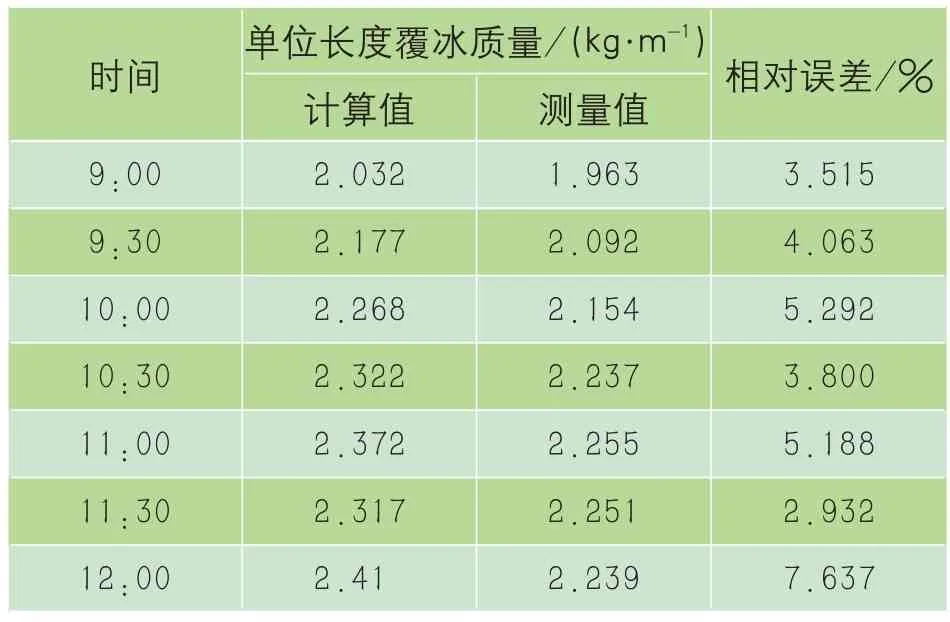
表5 覆有不规则厚冰时单位长度覆冰质量对比

由图6、图9可以看到，风荷载系数与瞬时风速的三次多项式拟合度很高，随着风速升高，风荷载系数越小，并且逐步趋于稳定；风速相同时，风荷载系数与覆冰导线迎风面积正相关，迎风面积越大，风荷载系数越大。

本方法是将覆冰导线视作一个整体计算风荷载，覆冰形状对风荷载计算的影响很小；当覆冰较薄时，计算最大相对误差10.187%，覆冰较厚时，计算最大相对误差7.637%，随着覆冰增长，误差有变大的趋势。

造成误差的主要原因：根据覆冰长度及厚度人为测量覆冰质量存在误差，当覆冰较薄，人为测量因素是引起误差的主要误差；计算模型假设，模型没有考虑覆冰导线张力共振分量，并且实际试验中可以观察测量到试验导线档中覆冰厚度会略大于两端覆冰厚度，但是本文理论采用导线抛物线构型，假设覆冰沿档距均匀分布，所以计算结果和试验结果会有误差；绝缘子及金具上的覆冰。由于拉力传感器假装在雨凇塔与绝缘子之间，此时测量张力内包含绝缘子及金具上的覆冰，对于覆有厚冰情况，计算导线覆冰质量总是大于测量值，此时绝缘子及金具上覆冰较重，不能忽略。当覆冰较厚，绝缘子及金具上的覆冰是引起误差的主要原因。

4 结束语

本文通过对覆冰导线进行力学分析，构建覆冰导线力学模型从静态及动态两个方向建立温度、覆冰导线冰荷载、瞬时风荷载与端部张力定量关系；将覆冰导线视为一个整体，提出风荷载系数，建立瞬时风下导线覆冰质量计算方法；于雪峰山野外观测站进行覆冰试验对瞬时风下导线覆冰质量计算方法可行性及泛用性进行验证。

温度变化，冰荷载以及风荷载都是改变覆冰导线端部张力的重要因素，综合以上因素提出瞬时风下覆冰动态张力计算公式。

根据公式提出无风以及有风情况下导线覆冰质量计算方法。

提出风荷载计算系数，风荷载系数与瞬时风速的三次多项式拟合度很高，随着风速升高，风荷载系数越小，并且逐步趋于稳定；风速相同时，风荷载系数与覆冰导线迎风面积正相关。

无风及有风情况导线覆冰质量计算方法精度满足工程计算要求；当覆冰较薄，人为测量冰重误差是主要误差，当覆冰较厚，绝缘子及金具上覆冰造成计算值偏大，是主要误差。