基于EMD与K-means的ILSTM模型在池塘溶解氧预测中的应用
谢雨茜,李路 ,2,朱明,2,谭鹤群,3,李家庆,宋均琦
1.华中农业大学工学院,武汉 430070;2.长江经济带大宗水生生物产业绿色发展教育部工程研究中心,武汉 430070;3.农业农村部水产养殖设施工程重点实验室,武汉 430070
溶解氧(dissolved oxygen,DO)含量(简称溶氧量)是衡量水质的最重要指标之一,不仅反映了水中生物产氧过程和耗氧过程之间的动态平衡,还直接影响养殖对象的产量和品质。目前水产养殖中大多是根据当前溶氧量决定增氧设备的启停[1],但水体环境系统具有较大惯性,如果仅根据当前数据进行调节,不仅难以及时改善恶化的水质,还会加重水质指标的震荡,不利于水产养殖对象的健康。因此,及时准确地进行池塘溶氧量预测,对提高水质调控精度、增加水产养殖效益具有重要意义。
近年来国内外很多学者对水体溶氧量预测方法进行了研究。其中,神经网络预测方法是运用最广泛的溶氧量预测方法,其包括反向传播神经网络、极限学习机、循环神经网络等。反向传播神经网络容易得到局部最优解,因此一般与遗传算法[2]或者粒子群优化相结合[3]使用。极限学习机结构简单,易获得全局最优解,且学习速度快、泛化性能好,若将其与K-means聚类结合,则能提高预测精度[4]。循环神经网络算法适合处理时间序列,它强调研究对象时间上的相关性。常用的循环神经网络是长短期记忆神经网络(long short-time memory,LSTM)与它的变体门控神经网络模型,特别适合预测溶氧量这种受多因素影响且时间依赖性强的数据,但若输入因素间关系复杂或预测时长过长,易导致预测结果滞后、误差增大的问题[5]。
本研究针对上述问题,提出一种基于经验模态分 解(empirical mode decomposition,EMD)与 K-means 的改进长短期记忆神经网络(improved long short-time memory neural network model based on empirical modal decomposition with K-means clustering,EMD-KILSTM)对池塘溶氧量进行预测。首先利用皮尔森相关性分析与主成分分析结合的方法对原始数据进行特征选择,然后利用EMD 算法对溶氧量时间序列进行分解。之后,将选出的环境参数与溶氧量各分量一起生成样本集,并对其进行K-means聚类,最后对同类中不同分解分量建立相应ILSTM预测模型,并用网格搜索、五折交叉验证与早停法进行超参数选取。以期减少LSTM 模型预测延迟现象、提高预测精度。
1 材料与方法
1.1 仪器设备
为了精准预测溶氧量,必须明确与其相关的环境参数,因此需要尽量全面地收集该池塘的水质与气象信息,使用相关性分析提取对溶氧量影响较大的参数。本研究根据相关文献[6],选出10 个影响溶氧量的环境参数,并使用基于物联网的远程监测系统采集池塘的水质数据与气象数据。
每种水质传感器都自带温度测量功能,相应的类型及详细参数:(1)荧光溶氧量传感器(NS-120ZGS)精度为±2.0%;(2)pH 传感 器(NPH-1000Z)精度为±1.7%;(3)氨氮传感器(NHNG-5000Z)精度为±4.0%。
气象传感器类型及详细参数如下:
(1)空气温湿度传感器(HMP155A-L),当温度为-80~20 ℃时,其精度为±(0.226-0.0028×温度)℃;当温度为20~60 ℃时,其精度为±(0.055+0.0057×温度)℃。(2)风速风向传感器(034B),当风速<10.14 m/s 时,精度为 0.1 m/s;当风速>10.14 m/s 时,精度为±1.1%。(3)气压传感器(CS100),量程为600~1 100 hPa,精度为±1.5 hPa。(4)太阳辐射计(LI200X-L),量程为0~3 000 W/m2,精度为±5%。(5)雨量计(TE525-L),精度为1%。
1.2 研究区域
以湖北省武汉市华中农业大学水产学院实验基地的8 号圈养池塘[7]为试验场地。该池塘面积约为1 166.66 m2,水深约2.8 m,在池塘内搭建了8 个直径为4 m、高3.1 m 的圈养桶,用以圈养鱼类。水质与气象传感器位置分布俯视图如图1。水质传感器在池塘正中心水深1 m 处,气象传感器位于池塘西北角。水质传感器采样周期为0.5 min,采集4 个参数分别为水温、氨氮、pH、溶氧量。气象传感器采样周期为5 min,采集7 个参数分别为气温、大气压强、湿度、雨量、太阳辐射强度(solar radiation intensity,SRI)、风速、风向。数据采集时间为 2021年 6 月 26 日-8 月17日。
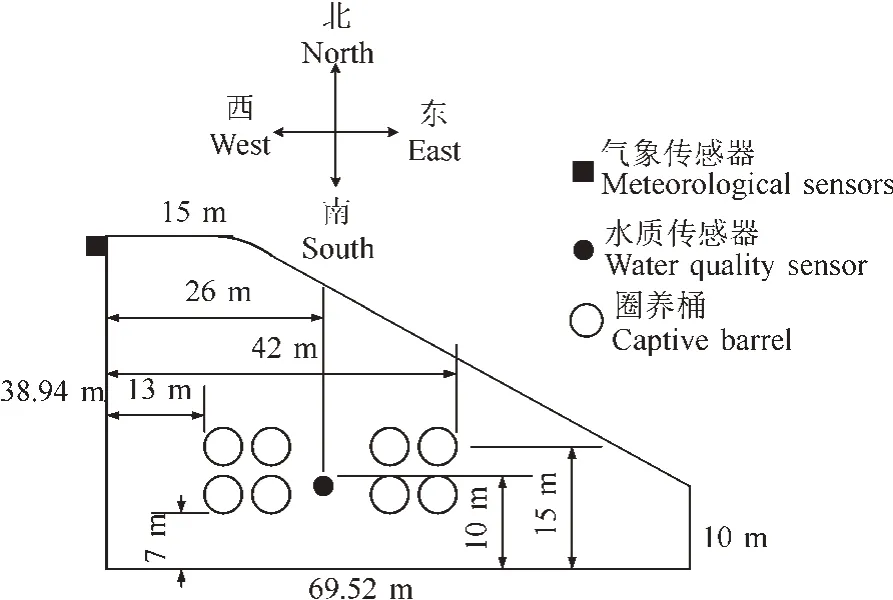
图1 水质与气象传感器的分布图Fig.1 Distribution of water quality and weather sensors
1.3 试验数据预处理
水质数据需要进行填充、修正、滤波、合并、归一化。而气象数据已经进行过降噪处理,只需对其进行合并、归一化即可。
1)数据的填充与修正。由于水质传感器自身的测量原理的局限性,造成在天然水域中容易产生异常值。同时水质传感器需要定期擦拭与校准,其间产生空缺值。针对这些问题,对采集水质数据进行填充与修正。因为水质数据在时间上具有连续性且采样周期是0.5 min,在短时间内池塘水质数据发生剧烈变化的可能性小,所以采用线性插值法填补丢失的数据,采用均值法修正异常值[8]。
2)移动平均滤波。在复杂的池塘养殖环境中,因水流波动、藻类附着等原因,导致采集的水质数据存在一定噪声干扰,因此要对水质数据进行滤波降噪。由于水质数据中的噪声频率相对稳定,可用移动平均滤波器来实现数据降噪。
3)数据合并。因气象数据与水质数据采集周期不一样,需要将两者在时间轴上与气象数据合并成采用周期5 min的数据。
4)归一化。利用Z-score标准化方法对数据进行归一化处理,使模型输入参数介于[0,1]之间,从而提升预测模型收敛速度与精度。
1.4 皮尔森相关性分析与主成分分析结合方法
将本文“1.2 中所述”11 个参数全部输入预测模型中,会增加模型训练时间、结构复杂程度与预测误差,所以需要在建模前进行特征提取。本研究选择皮尔森相关性分析与主成分分析[9]相结合的方法进行特征提取,具体步骤为:
①对经过预处理后的环境参数进行皮尔森相关性分析,将与溶氧量相关性最大的参数选为除溶氧量外第一个特征参数,相关性过小的参数淘汰。
②将其余m个参数组成一个特征空间,得到相关系数矩阵R=[rij]m×m,并计算其对应的特征值及特征向量。
③计算各个主成分贡献率τi如式(1),贡献率τi表示第i个主成分表征特征空间的程度。

而累计贡献率ηi由多个主成分贡献率τi叠加而成,计算公式如式(2):
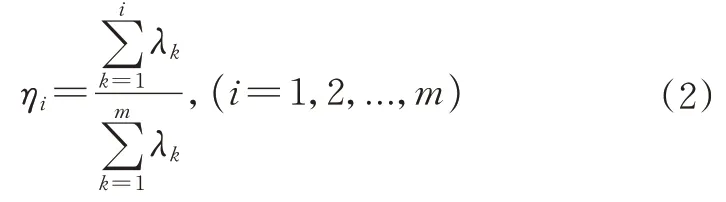
④原始参数线性组合成主成分的系数求法如式(3):

式(3)中,ωi为第i个主成分的系数,λi为该主成分对应的特征值,ξi为该主成分对应的特征向量。
选取特征值大于1 且累计贡献率大于70%的主成分来表征原始参数特征空间。在对应主成分的成分矩阵(特征向量表)中,筛选出最能解释样本空间数据的原始参数,从而完成特征提取。
1.5 模型建立方法
1)改进的长短期记忆神经网络。传统的LSTM神经网络的预测结果曲线与实测值曲线有一定滞后。原因在于,当采样间隔为step,时间窗长为d=3*step时,传统LSTM 模型样本形式如式(4):

式(4)中,虚线左侧为输入样本,右侧为输出样本。y(t+step)表示t+step 时刻溶氧量,x( )t为t时刻环境参数(溶氧量及其相关参数)。而当输入样本导入模型时,由于t时刻溶氧量与t+step 时刻预测目标高度相似,导致LSTM 神经网络给t时刻溶氧量分配过高的权重,最后使模型主要学习到时间序列的一阶自相关性,造成预测曲线的滞后。
解决滞后现象,有2 种思路:①将预测目标从未来时刻数值改成未来时刻数值和当前时刻数值的差分,直接预测一阶差分,防止模型学习到一阶相关性;②对目标时间序列进行分解,将其简化为若干简单波形再导入不同预测模型,分解形成的新波形因自身规律简单,更容易被预测模型学习。针对思路①,提出一种改进的LSTM 模型。将预测目标变为溶氧量的一阶差分,并使用滑动窗口法生成更多样本。ILSTM 神经网络整体结构如图2。
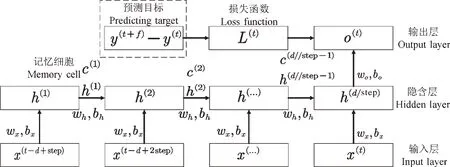
图2 ILSTM的整体结构图Fig.2 The overall structure of ILSTM
图2 中,wx,bx为输入层到隐含层的权重与偏置向量;wh,bh为隐含层内部单元的权重与偏置向量;w0,b0为隐含层到输出层的权重与偏置向量。图2中带入ILSTM 模型的输入输出为式(5):

式(5)中,step为样本间隔时间步数,单个时间步长为5 min;d为滑动窗口大小;f为预测未来时间步数为一个样本的输入参数向量为一个样本的预测目标;x(t-d+step),x(t-d+2step),...,x(t)为(td+step),...,t时刻的环境参数;y(t+f),y(t)为t+f,t时刻溶氧量。
该模型将预测目标从y(t+f)变成y(t+f)-y(t),直接消除训练模型过程中t时刻环境参数对t+f时刻预测的溶氧量影响大的问题,缓解预测结果的滞后现象。ILSTM 神经网络的隐含层内部单元结构与LSTM 神经网络一致[10]。
2)EMD 算法。该算法不像传统分解算法需要设定基函数,可直接根据数据在时间尺度上的特征进行分解[11],因此它非常适合像溶氧量这样的非平稳时间序列。本研究用EMD 将复杂的溶氧量时间序列分解为若干个单一频率的本征模函数(intrinsic mode function,IMF)与 残 余 分 量(residual,RES)如式(6):

每个IMF 蕴含溶氧量时间序列在不同时间尺度的局部特征信息,并且具有如下特性:①IMF 极值点数与过零点数最多相差1;②局部最大值与局部最小值形成的上下包络线的均值等于0。EMD 分解流程,如图3所示。

图3 EMD算法流程Fig.3 EMD algorithm flow
3)K-means 聚类算法。该算法属于无监督学习[12],适合分类未知类别的数据,缺点是需人工确定聚类数K。由于溶氧量受其环境影响大,可以利用K-means聚类来对环境参数生成的样本集进行分类,将具有相似历史环境的样本分为一类。
4)超参数优化细节如下:①网格搜索。设定各个超参数调节范围,利用网格搜索算法对其排列组合。
②交叉验证。用5 折交叉验证对选取的超参数组进行评价。本研究设定的评价指标为平均绝对误差(mean absolute error,MAE),其值越低,说明模型在训练集中表现得越优秀。
③早停法。为了缩短模型每次训练时间,本研究使用早停法提前退出迭代轮回。设定步数为5,即如果连续迭代5轮,验证集的损失函数都没下降即退出迭代。该方法可能会导致5 次交叉验证的迭代轮数不同,所以选择5次中最大轮数代表该组超参数的轮数。
5)EMD-KILSTM 预测模型。流程如图4 所示,具体步骤如下:①溶氧量时间序列分解。其简化了溶氧量时间序列复杂度,得到n个IMF和1个RES。

图4 EMD-KILSTM模型流程图Fig.4 Flow chart of EMD-KILSTM model
②对分解分量与环境因素进行K-means 聚类,导入聚类分析的样本形式如公式(7)。然后评估聚类算法的优劣,选出最优聚类情况。
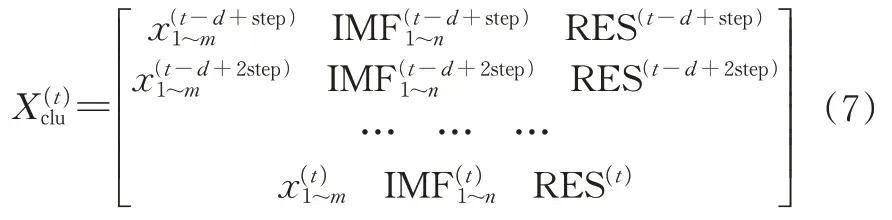
③在聚类得到的同类中对不同分解分量建立相应ILSTM 预测模型,进行超参数优化,然后将各分量的差分预测结果与该分量当前时刻值IMF(t)相加得到一个该分量未来值预测结果最后将每个分量相叠加成最终预测结果
1.6 模型评价指标
采用戴维森堡丁指数(Davies-Bouldin index,DBI)来衡量聚类数K值的合理性,其定义如式(8)。DBI越小,说明类内距离越小、相似度越高,且类间距离越大、相似度越低[13]。

式(8)中,Di,Dj分别为第i,j类内平均距离;dij为第i类与第j类的质心距离。
采用均方根误差(root mean square error,RMSE)、MAE、平均绝对百分比误差(mean absolute percentage error,MAPE)[14]3 个指标来衡量各预测模型的性能。
1.7 算法实现
本研究采用SPSS 软件做主成分分析。用Python3.6语言编写模型主要程序,详情见表1。
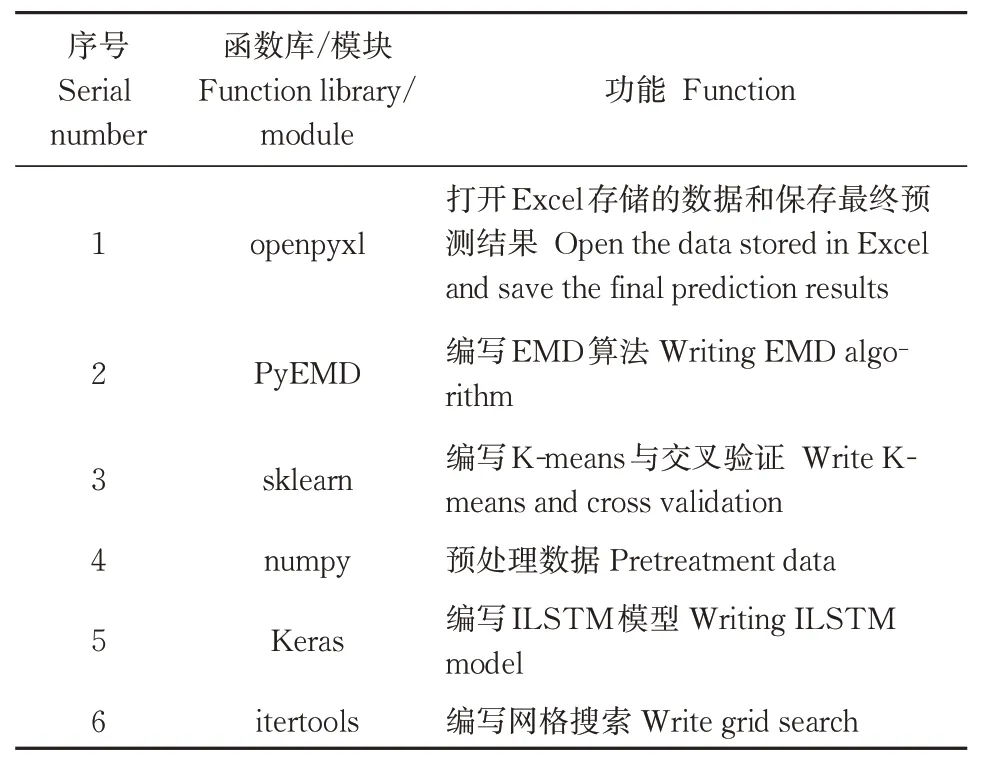
表1 Python编程信息Table 1 Python programming information
2 结果与分析
2.1 试验数据采集与预处理结果
对2021年06月26日-2021年08月17日共53 d所采集的140 000 条水质数据进行缺失值填补、异常值剔除与降噪的预处理,再与气象数据在时间维度上合并,最后得到15 264 条有效数据。各水质参数预处理结果(不包括归一化)如图5 所示。从图5A、图5C 的方框可见,预处理方法使数据抖动显著变小,噪声与异常值被有效剔除。预处理后各参数数据描述性统计见表2。

表2 参数描述性统计Table 2 Parameter descriptive statistics

图5 溶氧量(A)、pH(B)、氨氮(C)、水温(D)预处理对比Fig.5 Dissolved oxygen(A),pH(B),ammonia nitrogen(C),water temperature(D)pretreatment comparison
2.2 相关性分析结果
皮尔森相关性分析结果显示,溶氧量与雨量、风速、风向、SRI、气压、水温、氨氮、湿度、气温、pH 这10个参数的皮尔森相关性系数分别为0.046、0.128、0.134、0.241、-0.335、0.454、-0.538、-0.657、0.666、0.926。可见,pH 与溶氧量相关性最高,确定其为特征参数。而风速、风向、雨量相关性均低于0.2,因此将它们淘汰。剩下的6 个环境参数进行主成分分析,主成分贡献率与特征值见表3。从中可见有2 个特征值大于1 的主成分,并且贡献率高达74.095%。由主成分的成分矩阵(表4)可见,气温与湿度对第一个主成分影响较大,SRI对第二个主成分影响较大,最终选择的参数为DO、pH、气温、湿度、SRI。
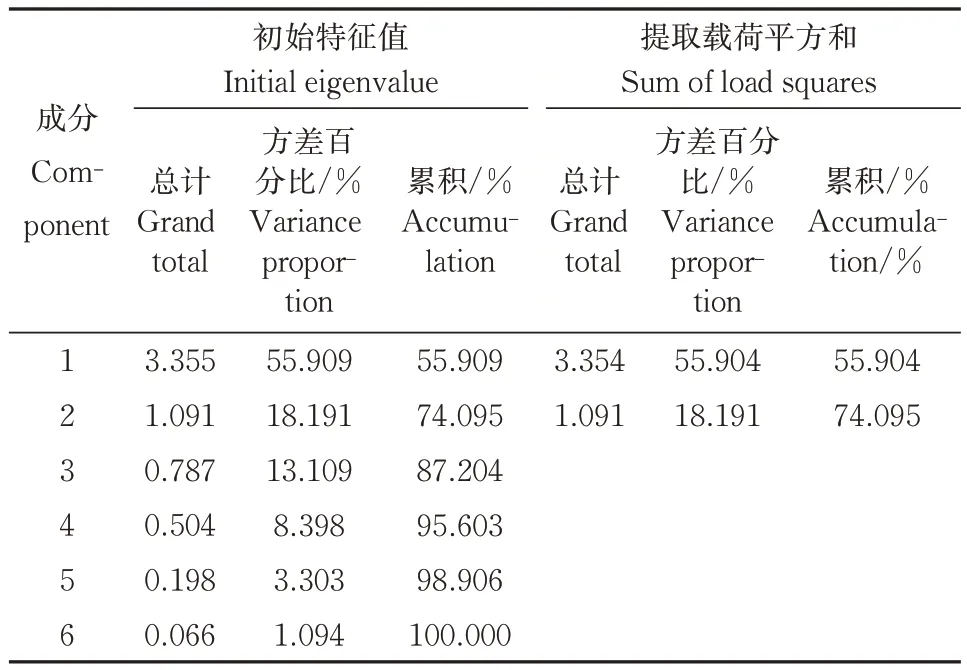
表3 主成分贡献率与特征值Table 3 Principal component contribution rate and eigenvalue

表4 成分矩阵Table 4 Component matrix
2.3 EMD分解结果
利用EMD 算法对溶氧量进行时间尺度上的分解,结果如图6 所示。由图6 可知,该算法将溶氧量分解为9个IMF 和1个RES。整体来看,池塘溶氧量具有明显的时间多尺度特点。其中IMF 具有一定周期性,能反映外部环境因素对溶解氧的周期性影响。IMF1~IMF4频率较高,体现了随机因素对溶解氧的影响。RES 变化较平稳,反映了池塘溶解氧的总体变化趋势。

图6 EMD分解溶氧量的结果Fig.6 Results of EMD decomposition of dissolved oxygen
2.4 K-means聚类结果
选前51 d 数据生成训练集,最后2 d 数据生成测试集,用于对比不同类型模型性能,预测目标为未来1 h 溶氧量。样本间隔时间步数step=12,单个时间步长为5 min;滑动窗口长度d=24×step;预测未来时间步数f=12,因此15 264 条有效数据可生成14 976 个样本集,前14 400 个样本用于模型训练,后576 个样本用于测试模型性能。样本输入参数形式如式(7),代入K-means 聚类中,不同的聚类数K的样本分类与其性能评价如表5。可见聚类数K为2时,分类效果最好,每个样本点类别分布如图7所示,将图7 与图5A 对比,发现低溶氧量波形被分为了一类,高溶氧量波形为一类。

图7 每个样本点类别分布Fig.7 Distribution of categories per sample point

表5 不同的聚类数K的样本分类与其性能评价Table 5 Sample classification with different number of clusters K and its performance evaluation
2.5 EMD-KILSTM预测结果及性能对比
将经过分解与分类的数据导入ILSTM 模型进行预测,此处输入参数的仅有溶氧量的分解分量,输入样本形式为(24,1),由于EMD 将溶氧量时间序列分解为10 个分量,K-means 聚类算法将每个分量都分为2类,因此需要得出20个不同情况的预测模型。
在超参数优化方面,网格搜索的信息见表6。有64 种超参数组合用于模型训练,20 个预测模型最优超参数与交叉验证评价见表7。从表7 中可知,频率越高的分解分量交叉验证的误差越大,这是因为频率越高,对应的IMF中的随机噪声成分越多。

表6 网格搜索的信息Table 6 Information about grid search

表7 20个预测模型最优超参与交叉验证评价Table 7 Evaluation of cross-validation and optimal super-reference for 20 prediction models
将本研究提出的EMD-KILSTM模型与LSTM、ILSTM、LSTM-SVR、EMD-LSTM、EMD-ILSTM等进行对比,各模型预测曲线如图8 所示,模型性能对比见表8,其中的时间复杂度与空间复杂度是对测试集使用时的复杂度;EMD-LSTM 模型、EMD-ILSTM 模型、EMD-KILSTM 模型均为单变量(仅分解分量)导入LSTM 模型中预测。其他模型是多变量输入LSTM 模型中预测。从图8A 方框可知LSTM预测有一定滞后现象,从图8B 与表8 可知,ILSTM与 LSTM 模型相比,RMSE、MAE 与 MAPE 分别下降了50.46%、63.20%与68.96%,说明ILSTM 模型能减少传统LSTM 模型预测滞后现象。从8C 可见ILSTM-SVR 比ILSTM 预测效果更好,但从其方框可看出,它在测试集的第2天,预测误差较大。图8D中,EMD-LSTM 模型比 EMD-LSTM5 模型精度高,说明溶氧量序列经过EMD 分解后的各分解分量在时间相关性上与其他参数不匹配,所以进行EMD 分解后的各分量仅能单独导入LSTM 模型。从表8 可得EMD-ILSTM 模型预测效果优于ILSTM 模型,RMSE、MAE 与 MAPE 分别下降了53.22%、46.74%与38.19%,说明EMD 算法能提高预测精度。从表8和图8 可知,EMD-KILSTM 模型是7 个预测模型中精度最高的,说明K-means 聚类能提高预测精度。EMD-ILSTM 模型预测未来1 h 溶氧量的RMSE、MAE、MAPE 分别为0.109 9 mg/L、0.074 9 mg/L、9.327 8%,其中MAPE 较大的原因是测试集属于低溶氧量时段,分母数值太小,MAPE 较敏感。EMD-KILSTM 与其他6 个模型的误差下降率见表9。

表8 模型性能对比Table 8 Comparisons of model performance
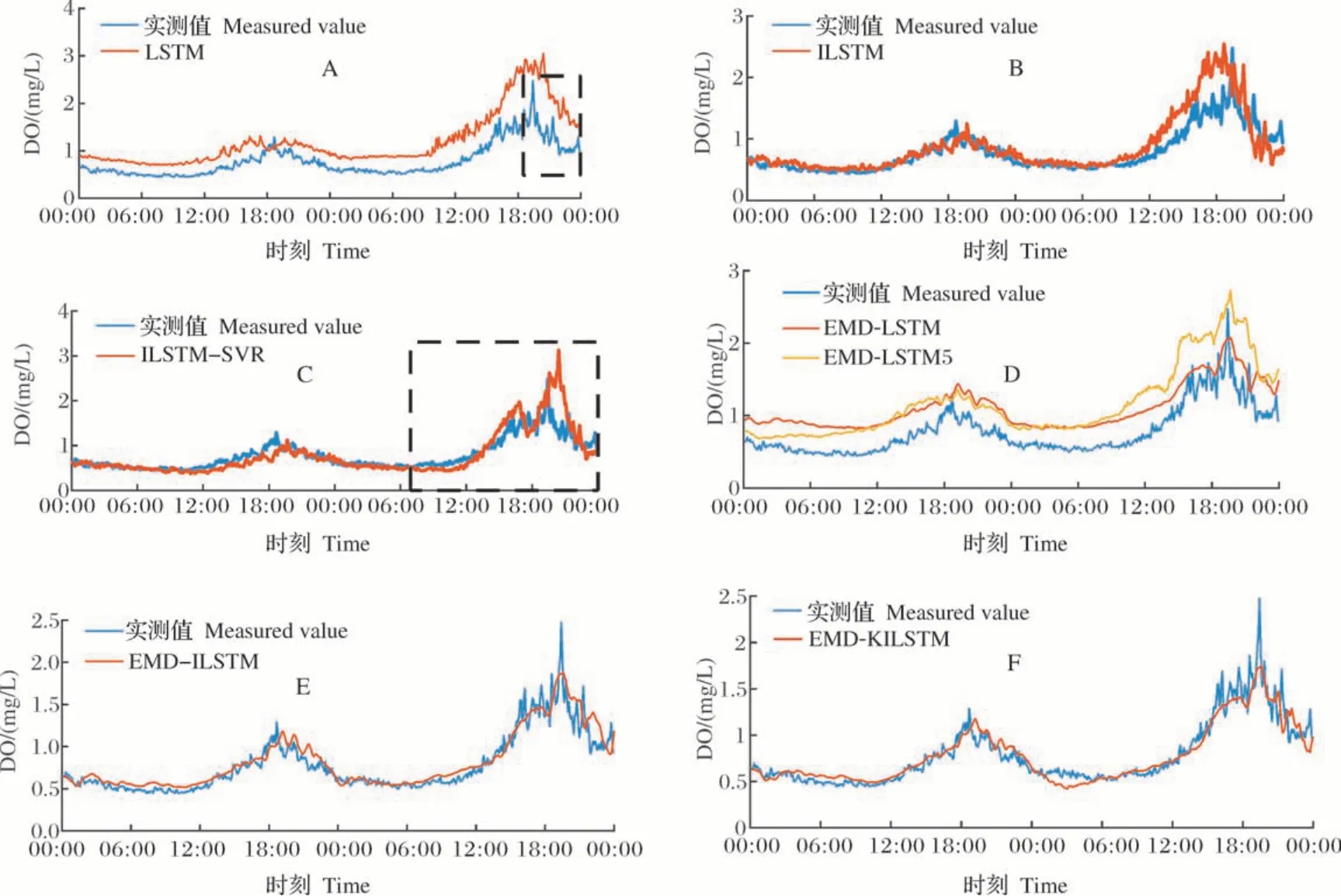
图8 LSTM模型(A)、ILSTM模型(B)、ILSTM-SVR模型(C)、EMD-LSTM模型与EMD-LSTM5模型(D)、EMD-ILSTM模型(E)、EMD-KILSTM模型(F)的预测结果Fig.8 Prediction results of LSTM model(A),ILSTM model(B),ILSTM-SVR model(C),EMD-LSTM model and EMD-LSTM5 model(D),EMD-ILSTM model(E),EMD-KILSTM model(F)

表9 EMD-KILSTM 与其他模型误差下降率Table 9 Error decline ratio of EMD-KILSTM to other models %
3 讨 论
EMD-KILSTM 模型是一种通过精细分类来预测溶氧量的方法。它能让养殖人员提前了解未来1 h池塘的溶氧量,更精确地调控增氧系统工作状态,对减小溶氧量波动,提升养殖对象环境舒适度并减少病害,提高养殖效益具有重要意义。
本研究提出的EMD-KILSTM 池塘溶氧量预测模型与自回归移动平均模型[15]相比,能同时考虑环境因素与历史溶氧量对未来溶氧量的影响,而自回归移动平均模型仅根据溶氧量线性自相关关系进行预测;与灰色预测模型[16]相比,EMD-KILSTM 池塘溶氧量预测模型能对溶氧量进行精准预测,而灰色预测模型只能估计溶氧量趋势;与支持向量机回归[17]相比,EMD-KILSTM 池塘溶氧量预测模型考虑了溶氧量在时间轴上的自相关性和各个环境参数的互相关性,而支持向量机回归只能考虑其中一种相关性;与LSTM 模型相比[18],本模型不仅减轻了传统LSTM 模型预测结果滞后的情况,还能将溶氧量依据时间尺度特征与历史环境情况自动分类,从而提高预测精度。后续拥有若干年数据时,也可以运用该方法,自动将类似环境的数据分为一类,从而做到在春夏秋冬、晴阴雨雪等各种天气模式下都能精准预测池塘溶氧量。
但EMD-KILSTM 模型也存在一些缺点需要改进:(1)虽然本研究提出的超参数优化方法涉及的超参数类型全面,但需要人为设定网格范围,寻找最优超参数组合速度慢,后续可能会与粒子群优化算法结合,提高模型训练速度;(2)仅用一种聚类算法进行分类,后续对多种聚类算法进行对比,择优确定最佳分类方案。

